وجد علماء الرياضيات مشكلة في المعادلات الشهيرة لوصف السوائل

أثبت اثنان من علماء الرياضيات أنه في ظل ظروف قاسية معينة ، فإن معادلات نافيير-ستوكس تعطي هراء

تصف معادلات Navier-Stokes بمساعدة عدة مصطلحات مقتضبة واحدة من أكثر الظواهر شيوعًا في العالم المادي: تدفق السوائل. واليوم ، تُستخدم هذه المعادلات ، التي يعود تاريخها إلى عشرينيات القرن التاسع عشر ، لوصف كل شيء بدءًا من تيارات المحيط والاضطراب بعد الطائرة إلى تدفق الدم إلى القلب.

على الرغم من أن الفيزيائيين يعتبرون هذه المعادلات موثوقة ، مثل المطرقة ، فإن علماء الرياضيات لا يثقون بها. بالنسبة لرياضيات ، فإن حقيقة أن هذه المعادلات تبدو فعالة لا تعني الكثير. إنهم بحاجة إلى دليل على أن المعادلات خالية من الأخطاء: بالنسبة لأي سائل وللتنبؤات طويلة المدى ، موزعة بقدر المستقبل ، لن تفشل رياضيات المعادلات. لم يكن من السهل العثور على مثل هذا الضمان. أول شخص أو فريق يمكنه إثبات أن معادلات Navier-Stokes ستعمل دائمًا - أو تقديم مثال يثبت أنها لا تعمل - سيتمكن من الحصول على مكافأة لحل إحدى مشكلات الألفية ، التي أعلن عنها معهد Clay's الرياضي ، ومليون دولار في إضافة [اعتبارًا من عام 2017 ، تم حل واحدة فقط من المهام السبع للألفية (فرضية بوانكاريه) بواسطة غريغوري بيرلمان / تقريبا. ترجم.].

طور علماء الرياضيات عدة طرق لحل هذه المشكلة. يطرح العمل الجديد ، الذي نُشر في سبتمبر ، أسئلة جدية حول ما إذا كان أحد الأساليب الأكثر شيوعًا للمشكلة ، والذي تم تطويره على مدار سنوات عديدة ، يمكن أن ينجح. العمل ، الذي كتبه تريستان بوكماستر وفلاد فيكول من جامعة برينستون ، هو أول نتيجة توضح كيف ، في ظل ظروف معينة ، تعطي معادلات نافير-ستوكس وصفًا متناقضًا للعالم المادي.

يقول بوكماستر: "نحاول أن نفهم بعض المشاكل المتأصلة في هذه المعادلات ، ولماذا قد يضطر الناس إلى إعادة التفكير فيها".

يُظهر عمل Buckmaster و Wikol أنه إذا قمت بافتراضات تقريبية جدًا عند حل معادلات Navier-Stokes ، فلن يكون لها أي معنى: يقولون أن نفس السائل مع نفس الظروف الأولية يمكن أن يأتي في حالتين مختلفتين أو أكثر. يمكن أن تتدفق بطريقة واحدة ، أو بطريقة مختلفة تمامًا. إذا كان الأمر كذلك ، فلا يمكن لهذه المعادلات أن تصف بشكل موثوق العالم المادي الذي تم تطويره من أجله.

تفجير المعادلات

لفهم كيف يمكن أن تنكسر المعادلات ، تخيل تيار المحيط. في إطارها ، يمكن أن تتواجد التدفقات المحلية ، ونتيجة لذلك يمكن أن تتحرك بعض أجزائها في اتجاه واحد وبسرعة واحدة ، والبعض الآخر في اتجاه آخر بسرعة أخرى. تتفاعل التدفقات المحلية مع بعضها البعض في العمل المتبادل المستمر للاحتكاك وضغط المياه ، والتي تحدد تدفقها.

يقوم علماء الرياضيات بوضع نموذج لهذا التفاعل باستخدام خريطة تخبرك بالاتجاهات ومعدلات التدفق في أي نقطة في السائل. هذه الخريطة ، التي تسمى حقل ناقل ، هي لقطة للديناميكيات الداخلية للسائل. تلتقط معادلات Navier-Stokes هذه الصورة وتعيد إنتاجها كفيديو ، تخبرنا كيف سيبدو حقل المتجه بالضبط في كل لحظة لاحقة في الوقت المناسب.


تعمل خريطة الرياح (windy.com) بطريقة مشابهة لحقل ناقل. عند كل نقطة ، يكون للرياح اتجاه وقوة معينة.

تعمل هذه المعادلات. يصفون تدفق السوائل بشكل موثوق به كما تتوقع معادلات نيوتن المواقع المستقبلية للكواكب. يستخدمها الفيزيائيون باستمرار ، ويتوافقون باستمرار مع نتائج التجارب. ومع ذلك ، يحتاج علماء الرياضيات إلى أكثر من التأكيد العرضي - فهم بحاجة إلى دليل على أن المعادلات لا تنتهك ، بغض النظر عن مجال المتجه الذي تبدأ منه ومدى إعادة إنتاجه في المستقبل ، ستعطيك المعادلات دائمًا حقل ناقل جديد وفريد.

هذا هو موضوع مشكلة الألفية ، يسأل عما إذا كانت معادلات Navier-Stokes لها حلول (الحل ، في الواقع ، هو حقل ناقل) لجميع نقاط البداية في جميع النقاط في الوقت المناسب. يجب أن تضمن هذه الحلول الاتجاه الدقيق وقوة التدفق عند كل نقطة في السائل. تسمى الحلول التي توفر معلومات بمثل هذه الدقة الصغيرة بشكل لا نهائي "السلس". للحصول على حل سلس ، تحتوي كل نقطة في الحقل على ناقل مرتبط بها ، مما يسمح لك بالسفر "بسلاسة" حول الحقل دون الوقوع في النقاط التي يكون فيها المتجه غائبًا - في نقطة لن تفهم منها الحركة الإضافية.

الحلول السلسة هي تمثيل كامل للعالم المادي ، ولكن من وجهة نظر رياضية ، قد لا تكون موجودة دائمًا. علماء الرياضيات الذين يعملون على معادلات مثل هذه قلقون بشأن هذا الموقف: تقوم بتشغيل معادلات Navier-Stokes وتلاحظ التغييرات في مجال المتجه. بعد مرور بعض الوقت المحدود ، تخبرك المعادلات أن جزيء معين من السوائل يتحرك بسرعة لا نهائية. ثم سيكون لديك مشاكل. تشمل المعادلات قياس التغيرات في خصائص مثل الضغط والاحتكاك وسرعة السوائل - يتحدثون بلغة ، يأخذون مشتقات هذه الكميات - ولكن ليس من الأسهل أخذ مشتق كمية لا حصر لها من القسمة على صفر. لذا ، إذا أعطت المعادلات قيمة لا نهائية ، فيمكننا القول أنها رفضتك ، أو "انفجرت". لم يعد بإمكانهم وصف الحالات اللاحقة للسائل.

مثل هذا "الانفجار" هو دليل على أن المعادلات تفتقر إلى وصف لبعض خصائص العالم المادي التي يجب أن تصفها. يقول بوكماستر: "ربما لا تغطي المعادلات جميع تأثيرات المائع الحقيقي ، لأنه في المائع الحقيقي لا نتوقع سرعة لا متناهية من الجسيمات".

الحل لمشكلة الألفية هو إما إظهار أن معادلات Navier-Stokes لا تنفجر أبدًا ، أو لإيجاد الظروف التي يحدث فيها ذلك. تتمثل إحدى الاستراتيجيات التي يستخدمها علماء الرياضيات في تخفيف متطلبات كيفية دقة هذه المعادلات لوصف الحلول المطلوبة.

اضطراب التدفق

يجب أن تصف معادلات Navier-Stokes تدفق أي سائل ، مع أي ظروف أولية ، وتمديد الوصف إلى ما لا نهاية في المستقبل. في محاولة لإثبات هذه القدرة ، يقوم علماء الرياضيات أحيانًا "بالضعف" ، أي أنهم يستخدمون أوصافًا تقريبية لحقول المتجهات تصف السوائل. لكن هناك صعوبات في ذلك.

من الناحية المثالية ، يريد علماء الرياضيات إثبات أن تطبيق معادلات Navier-Stokes على أي سائل "سلس" مستمر سيؤدي إلى نتيجة فريدة واحدة.



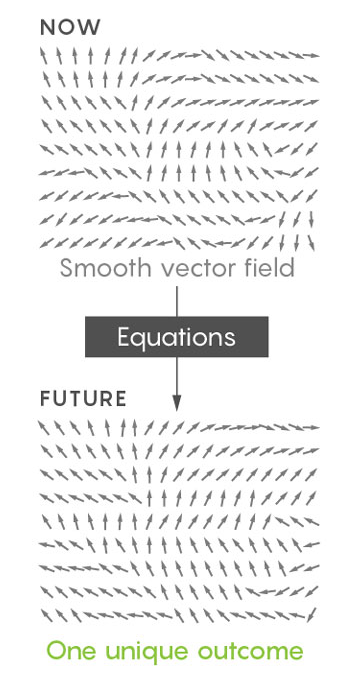
ومع ذلك ، من الأسهل العمل مع حقول المتجهات "الضعيفة" ، وليس بالتفصيل. وقد وجد علماء الرياضيات أن بعض الأوصاف الضعيفة تؤدي إلى نتائج غير فريدة - فهي تسمح لنفس السائل بالتدفق في نفس الظروف الأولية بطريقتين.

من ضعيف إلى سلس

عندما يدرس علماء الرياضيات معادلات كهذه ، يبدأون أحيانًا بتوسيع تعريف ما يشكل الحل. تتطلب الحلول السلسة أقصى قدر من المعلومات - في حالة Navier-Stokes ، تتطلب وجود ناقل في كل نقطة في حقل المتجه المرتبط بالسائل. ولكن ماذا لو قمنا بتخفيف المتطلبات وقلنا إنك تحتاج إلى حساب المتجهات فقط لبعض نقاط المجال ، أو تحتاج إلى الحصول على القيم التقريبية للمتجهات فقط؟ تسمى هذه القرارات "ضعيفة". إنها تسمح لعلماء الرياضيات أن يشعروا بسلوك المعادلة دون المهمة الشاقة المتمثلة في إيجاد جميع الحلول على الإطلاق (والتي قد لا تكون ممكنة عمليًا).


تريستان بوكماستر ، عالم رياضيات في جامعة برينستون

قال كاميلو دي ليليس ، الذي شارك في تأليفه مع Lazlo Schekelikhidi ، الذي كتب العديد من الأعمال المهمة التي أرست الأساس لعمل بوكماستر وفيكولا: "من وجهة نظر معينة ، فإن القرارات الضعيفة أسهل في الوصف من تلك الحقيقية ، لأنك تحتاج إلى معرفة أقل بكثير".

تأتي الحلول الضعيفة في درجات مختلفة. إذا كنت تتخيل حلًا سلسًا في شكل صورة رياضية لسائل ذي دقة لا نهائية ، فستكون الحلول الضعيفة شيئًا مثل إصدارات 32 بت أو 16 بت أو 8 بت من هذه الصورة.

في عام 1934 ، حدد عالم الرياضيات الفرنسي جان لاري فئة مهمة من الحلول الضعيفة. بدلاً من العمل مع المتجهات الدقيقة ، تأخذ "حلول Leray" متوسط ​​قيمة المتجهات في حي صغير من حقل المتجه. أثبت Leray أنه يمكنك دائمًا حل معادلات Navier-Stokes ، مما يسمح لقراراتك بأخذ شكل من هذا النوع. بعبارة أخرى ، لا تنفجر قرارات ليرا.

حدد إنجاز Lera نهجًا جديدًا لمشكلة Navier-Stokes: ابدأ بحلول Lera ، التي يعرف وجودها بالفعل ، وانظر إذا كان يمكن تحويلها إلى حلول سلسة تريد إثبات وجودها. تشبه هذه العملية العملية التي تبدأ فيها بصورة تقريبية ، ومعرفة ما إذا كان بإمكانك لف الدقة تدريجيًا لتحقيق الصورة المثالية للواقع.

قال باكماستر "إحدى الاستراتيجيات الممكنة هي إظهار أن قرارات ليرا الضعيفة هذه سلسة ، وإذا تمكنت من إظهار أنها سلسة ، فسوف تحل تحدي الألفية".


يمثل فلاد فوكول نصف الفريق الذي كشف عن مشكلات في طريقة التحقق من معادلات Navier-Stokes.

هناك صيد آخر. تتوافق حلول معادلات Navier-Stokes مع الأحداث المادية الحقيقية ، وتحدث الأحداث المادية بطريقة واحدة ممكنة. بالنظر إلى ذلك ، أود أن تحتوي معادلاتك على مجموعة واحدة فقط من الحلول الفريدة. إذا أعطتك المعادلات العديد من الحلول الممكنة ، فلا يمكنها القيام بعملها.

لذلك ، سيتمكن علماء الرياضيات من استخدام حلول Leray لحل مشكلات الألفية ، فقط إذا كانت حلول Leray فريدة. ستعني حلول Leray غير الفريدة أنه وفقًا لقواعد Navier-Stokes ، يمكن أن يأتي نفس السائل مع نفس الظروف الأولية إلى حالتين فيزيائيتين مختلفتين ، ليس لهما معنى مادي ، ويعني أن المعادلات لا تصف في الواقع ماذا يجب.

النتيجة الجديدة لـ Bakmaster و Wikol هي التلميح الأول الذي يمكن أن يحدث هذا لبعض التعريفات للقرارات الضعيفة.

عوالم كثيرة

في عملهم الجديد ، ينظر كل من Buckmaster و Wikol في حلول أضعف من حلول Leray - الحلول التي تستخدم نفس مبدأ المتوسط ​​مثل Leray ، ولكنها تضعف متطلبًا إضافيًا آخر (يُعرف بعدم المساواة في الطاقة). يستخدمون طريقة "التكامل المحدب" ، والتي تنبع من العمل على هندسة عالم الرياضيات جون ناش ، وتشارك لاحقًا في دراسة السوائل بواسطة دي ليليس وشيكيليكيدي.

باستخدام هذا النهج ، يثبت Buckmaster و Wikol أن هذه الحلول الضعيفة جدًا لمعادلات Navier-Stokes ليست فريدة. على سبيل المثال ، يوضحون أنه إذا بدأت بسائل هادئ تمامًا ، على سبيل المثال ، مع كوب من الماء بجوار السرير ، فقد يكون هناك نوعان من الأحداث. الأول واضح: الماء يبدأ بحالة هادئة ويظل دائمًا هادئًا. والثاني رائع ، لكنه ممكن رياضياً: يبدأ الماء من حالة هادئة ، وينفجر في منتصف الليل ، ثم يعود إلى حالة هادئة.

يقول فيكول: "يثبت هذا الافتقار إلى التفرد ، لأنه يمكن إنشاء شيئين على الأقل من البيانات الأولية".

أثبت Buckmaster و Wikol وجود العديد من الحلول الضعيفة غير الفريدة (ليس فقط الحلين الموصوفين أعلاه) لمعادلات Navier-Stokes. أهمية هذا الدليل لا يزال يتعين فهمه. في مرحلة ما ، يمكن أن تصبح الحلول الضعيفة ضعيفة جدًا بحيث تتوقف عن الارتباط بالحلول الأكثر سلاسة التي يجب أن تقلدها. إذا كان الأمر كذلك ، فإن النتيجة التي حصل عليها Bakmaster و Wikol لن تؤدي إلا إلى القليل.

"هذه النتيجة هي تحذير واضح ، ولكن يمكن للمرء أن يجادل بأن هذا التحذير يتعلق أضعف فكرة القرارات الضعيفة. هناك العديد من طبقات الحلول الأقوى التي يمكنك أن تأمل في سلوك أفضل بكثير "في حالة معادلات Navier-Stokes ،" يقول De Lellis.

يفكر باكماستر وويكول أيضًا من حيث الطبقات ، وقد وضع نصب عينيه قرارات لير - على إثبات أنهم يعترفون أيضًا بالفيزياء المتعددة التي يمكن أن يأتي فيها السائل نفسه من نفس الحالة إلى أشكال مختلفة في المستقبل.

"تريستان وأنا أعتقد أن قرارات ليراي ليست فريدة. لم نثبت ذلك بعد ، لكن عملنا يضع رأس الجسر لهجوم على هذه المهمة.