يعتزم الفيزيائيون تصنيف جميع مراحل المادة

يمكن أن يؤدي التصنيف الكامل إلى عدد كبير من المواد والتقنيات الجديدة. ومع ذلك ، لا تزال المراحل الأكثر غرابة تقاوم فهم العلماء

على مدى العقود الثلاثة الماضية ، اكتشف خبراء في فيزياء المادة المكثفة بلدًا رائعًا من أطوار المادة الغريبة الجديدة: تظهر فجأة حالات جماعية للجسيمات المتفاعلة التي تختلف تمامًا عن الحالات الصلبة أو السائلة أو الغازية المعروفة للجميع.

تظهر هذه المراحل ، كما فهم البعض في المختبرات ، وبعضها يعتمد على الحسابات النظرية ، عندما تبرد المادة إلى درجة حرارة الصفر المطلق تقريبًا ، والتي تكون أكثر من مائتي درجة تحت نقطة تجمد الماء في الظروف العادية. في ظل هذه الظروف الباردة ، يمكن أن تتفاعل الجسيمات بطرق تجعلها تتخلص من كل آثار هويتهم السابقة. اكتشفت تجارب الثمانينيات أنه في بعض الحالات ، يتم فصل الإلكترونات إلى أجزاء من الجسيمات التي يمكن أن تترك آثارًا في الزمكان على شكل ضفائر . في حالات أخرى ، تظهر إصدارات لا حصر لها من بينها. يصبح شعرية ذرات الغزل سائلة من حلقات الغزل أو سلاسل المتفرعة ؛ تبدأ البلورات التي لم توصل الكهرباء في البداية بتمرير التيار فوق السطح. إحدى المراحل التي صدمت الخبراء ، عندما تم إثباتها رياضياً لأول مرة في عام 2011 ، تتضمن كيانات غريبة للغاية ، " فركتونات " تتشابك مع بعضها البعض في أنماط فركتالية [وفقًا لويكي ، فكتورونات هي تماثل فركتوني للفونونات ، وكمية الحركة الذبذبية للذرات الكريستال / تقريبا. ترجم.].

تتنافس الآن فرق البحث من Microsoft وشركات أخرى على كتابة المعلومات الكمية في أسلاك التوصيل المصنوعة والحلقات لبعض هذه المراحل من أجل تطوير جهاز كمبيوتر كمومي. وفي الوقت نفسه ، أجرى منظري فيزياء المادة المكثفة (CS) مؤخرًا العديد من الدراسات الأكثر أهمية لفهم مخططات السلوك الجماعي من أجل ترقيم وتصنيف جميع المراحل الممكنة للمادة. إذا نجحوا في تجميع تصنيف كامل ، فلن يسمح فقط بوصف جميع مراحل المادة التي يتم رؤيتها في الطبيعة في الطبيعة ، بل سيشير أيضًا إلى طريقة الحصول على مواد وتقنيات جديدة.

قام الباحثون ، بقيادة العشرات من أفضل المنظرين وبمساعدة علماء الرياضيات ، بتصنيف سيارة كاملة من المراحل قادرة على الظهور في أبعاد مكانية واحدة أو بعدين ، وربطها بالطوبولوجيا: مع الرياضيات التي تصف الخصائص غير المتغيرة لهذه الأشكال مثل المجال أو الحيد. كما تطرقوا إلى غابة الأطوار الناشئة في منطقة الصفر المطلق في مادة ثلاثية الأبعاد.


شي تشين ، منظّر المواد المكثف في معهد كاليفورنيا للتكنولوجيا

قال مايكل زاليتل ، المنظر في لجنة الاتصالات الفيدرالية في جامعة برينستون ، إن العلماء يبحثون عن "ليس قانونًا محددًا للفيزياء". "إنهم يبحثون عن مساحة من جميع الاحتمالات ، وهذا هو إلى حد ما فكرة أعمق وأجمل." قد يكون هذا غير متوقع ، ولكن ، كما يقول زاليتل ، فإن مساحة جميع المراحل المتسقة في حد ذاتها هي كائن رياضي "بهيكل غني بشكل لا يصدق ، والذي نعتقد أنه في عالم أحادي البعد وثنائي الأبعاد ، يتطابق واحد في واحد مع هذه الهياكل الطوبولوجية الجميلة" .

قال Ashvin Vishwanath من جامعة هارفارد هناك "اقتصاديات الخيارات" عبر المناظر الطبيعية لجميع المراحل. "وكل ذلك يبدو معروفًا" - مثل هذا الحظ يحيره. قال فيسواناث إن ترقيم أطوار المادة يمكن أن يتحول إلى شيء "مثل جمع الطوابع" ، "كل منها مختلف قليلاً عن الآخر ، ولا يوجد اتصال بينهما". بدلاً من ذلك ، فإن تصنيف المرحلة يشبه إلى حد كبير "الجدول الدوري". هناك العديد من العناصر فيه ، لكنها مقسمة إلى فئات ويمكننا فهم هذه الفئات ".

قد لا يبدو تصنيف السلوك الظاهر للجسيمات أساسيًا جدًا ، لكن بعض الخبراء ، على سبيل المثال ، Si- Gang Wen من معهد ماساتشوستس للتكنولوجيا ، يقولون أن القواعد الجديدة للمراحل الظاهرة تظهر كيف يمكن أن تنشأ الجسيمات الأولية نفسها على خلفية وهي تستند إلى شبكة من الأجزاء المتشابكة من المعلومات الكمية ، والتي يطلق عليها Ven "محيطات البتات". على سبيل المثال ، في مرحلة " مائع شبكة السلسلة " ، والتي يمكن أن تظهر نفسها في نظام ثلاثي الأبعاد للكيوبت ، تبدو الاضطرابات تمامًا مثل الجسيمات الأولية المعروفة. يقول فين: "الإلكترون الحقيقي والبروتون الحقيقي لا يمكن أن يكونا تقلبات إلا في شبكة الأوتار".

ترتيب طوبولوجي جديد

قبل ظهور هذه المراحل فجأة عند درجة حرارة صفر ، اعتقد الفيزيائيون أن جميع المراحل معروفة لهم بالفعل. وبحلول الخمسينات من القرن الماضي ، كان بإمكانهم بالفعل تفسير ما يحدث ، على سبيل المثال ، عندما يتحول الماء إلى جليد ، واصفين إياه بأنه انتهاك للتناظر: إذا كان الماء السائل له تناظر دوران على المستوى الذري (هو نفسه في جميع الاتجاهات) ، فإن جزيئات الجليد H ₂ O محاطة بأعمدة وصفوف.

تغير كل شيء في عام 1982 بعد اكتشاف تأثير هول الكم الجزئي ، والذي يتجلى في غاز ثنائي الأبعاد فائق الإلكترون للإلكترونات. تمتلك مادة في هذه الحالة جسيمات واضحة مع شحنات في جزء صغير من شحنات الإلكترون ، مما يجعل أجزاء من الخطوات في محيط أحادي الجانب لمحيط النظام. قال فين: "باستخدام التناظر ، كان من المستحيل بالفعل التمييز بين هذه المراحل".

كان هناك حاجة لنموذج جديد. في عام 1989 ، قدم فين أن أطوارًا مثل حالة تأثير هول الكم الجزئي لا تظهر على متن الطائرة ، ولكن على مجموعات طوبولوجية أخرى - أسطح متصلة مثل سطح الكرة أو الحيد. يشير الطوبولوجيا إلى الخصائص العالمية الثابتة لمثل هذه المساحات التي لا يمكن تغييرها عن طريق التشوه المحلي. كما تعلم ، على الأقل بالنسبة للطبوغرافيين ، يمكنك تحويل الكعك إلى كوب عن طريق تشويه سطحه ، نظرًا لأن كلا الشكلين لهما ثقب واحد ، وبالتالي ، فإنهما متكافئين طبولوجيا. لكن التمدد والضغط بقدر ما تريد ، وحتى الكعكة الأكثر مرونة لا يمكن تحويلها إلى البريتزل.

اكتشف فين أنه في ظل الظروف الطوبولوجية الجديدة ، تظهر خصائص جديدة في مراحل درجة حرارة صفر ، وصاغ مصطلح " الترتيب الطوبولوجي " ، الذي يصف جوهر هذه المراحل. اكتشف منظّرون آخرون أيضًا علاقة بين المراحل والطبولوجيا. مع اكتشاف العديد من المراحل الغريبة المختلفة - هناك الكثير منها لدرجة أن الباحثين يقولون إنهم بالكاد يمكنهم مواكبتها - أصبح من الواضح أن الطوبولوجيا والتماثل يوفران نظامًا جيدًا لتنظيمها.

تظهر المراحل الطوبولوجية فقط في منطقة الصفر المطلق ، لأنه فقط في درجات الحرارة المنخفضة هذه يمكن أن تدخل أنظمة الجسيمات الحالة الكمية الأرضية بأقل طاقة. في الحالة الأرضية ، فإن التفاعلات الدقيقة التي تحدد هوية الجسيمات - تختفي في درجات حرارة عالية - تربط الجسيمات في أنظمة عالمية باستخدام التشابك الكمي. وبدلاً من وصف الجسيمات بشكل فردي ، تصبح رياضيًا مكونات دالة أكثر تعقيدًا تصفها جميعًا دفعة واحدة ، غالبًا مع ظهور جسيمات جديدة في شكل إثارة المرحلة العالمية. تتحول المخططات الناشئة عن التشابك بعيد المدى إلى أنها طوبولوجية ، أي أنها غير حساسة للاضطرابات المحلية - مثل عدد الثقوب في مجموعة.


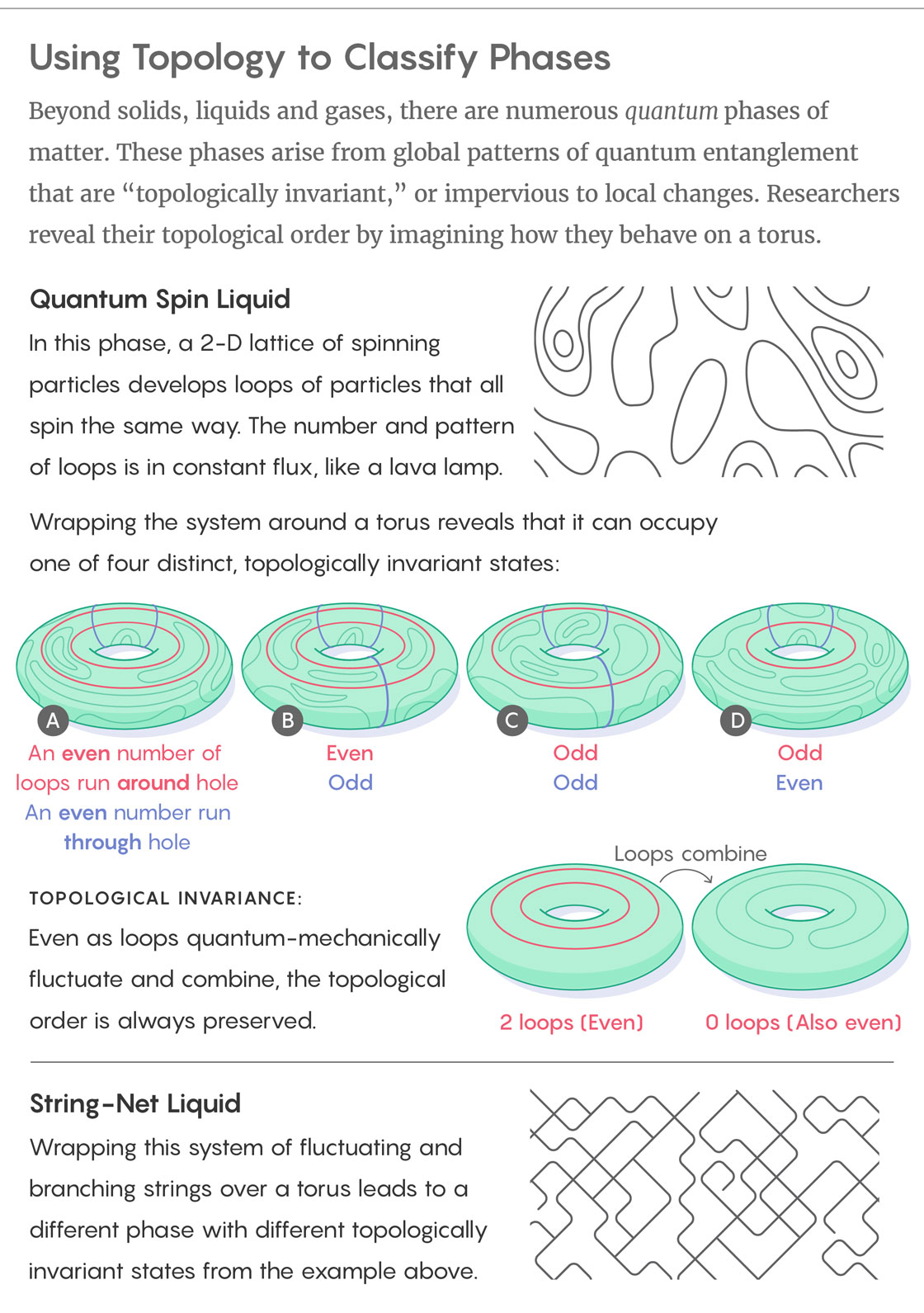أعلاه: طور الدوران السائل الكمي. في هذه المرحلة ، تؤدي شبكة ثنائية الأبعاد من الجسيمات الدوارة إلى ظهور حلقات الجسيمات الدورية بالتساوي. يتغير عدد وترتيب الحلقات طوال الوقت ، وكل هذا يشبه مصباح الحمم البركانية .

إذا قمت بتدوير هذا النظام على حيد ، يتبين أنه يمكن أن يشغل أربع حالات مختلفة طوبولوجية ثابتة:
أ) حول الفتحة: عدد زوجي من الحلقات / خلال الفتحة: عدد زوجي من الحلقات.
ب) زوجي / فردي.
ج) فردي / فردي.
د) فردي / زوجي.

على الرغم من حقيقة أن الحلقات تواجه باستمرار تقلبات ميكانيكا كمية ، يتم الحفاظ على الترتيب الطوبولوجي دائمًا (يمكن أن تصل الحلقتان إلى 0 حلقة ، وهو أيضًا رقم زوجي).

أسفل: سائل شبكة السلسلة. إذا قمنا بتغليف الحيد بنظام سلاسل متغيرة ومتفرعة ، فسوف نحصل أيضًا على حالات مختلفة طوبوغرافية.

ضع في اعتبارك أبسط مرحلة طوبولوجية لنظام يسمى "مائع السبين الكمومي" ، الذي يتكون من شبكة ثنائية الأبعاد من السبينات ، أو جسيمات تشير لأعلى أو لأسفل ، أو ، مع بعض الاحتمالات ، في نفس الوقت في كلا الاتجاهين. عند درجة الحرارة الصفرية ، يولد السائل الدوراني سلاسل من الس spين تشير في اتجاه واحد إلى الأسفل ، وتشكل هذه السلاسل حلقات مغلقة. يخضع اتجاه السبينات لتقلبات ميكانيكا كمية ، كما يتغير نمط الحلقات على المادة: يتم دمج حلقات السبينات السفلية في حلقات أكبر أو مقسمة إلى حلقات أصغر. في هذه المرحلة من مائع السبين الكمومي ، تكون الحالة الأساسية للنظام تراكبًا كميًا لجميع أنماط الحلقة المحتملة.

لفهم سبب كون مخطط التشابك هذا ترتيبًا طوبولوجيًا ، تخيل كيف فعله فين ، وأن سائل الكم يدور على سطح الحيد ، وبعض الحلقات تلتوي حول افتتاحه. وبسبب هذا ، فبدلاً من الحصول على حالة أرضية واحدة مرتبطة بتراكب جميع أنماط الحلقة ، سيوجد سائل الدوران في واحدة من أربع حالات أرضية مختلفة مرتبطة بأربع تراكبات من أنماط الحلقة. تتكون حالة واحدة من جميع أنماط الحلقة الممكنة مع عدد زوجي من الحلقات المحيطة بفتحة الحيد ، ومع عدد زوجي من الحلقات التي تمر عبرها. وللآخر الرقم الأول زوجي ، والثاني فردي. الثالث والرابع لديهم هذه الأرقام ، على التوالي ، فردي / زوجي و فردي / فردي.

ومرة واحدة في إحدى هذه الحالات ، يبقى النظام فيها ، على الرغم من حقيقة أن نمط الحلقة يتغير محليًا طوال الوقت. على سبيل المثال ، إذا كان مائع السبين لديه عدد متساوٍ من الحلقات المحيطة بفتحة الحيد ، عندها يمكن أن تلمس هاتان الحلقتان وتتحدان معًا وتتحول فجأة إلى حلقة لا تحيط بالفتحة على الإطلاق. يتم تقليل عدد الحلقات بمقدار اثنين ، ولكن لا يزال حتى. الحالة الأساسية للنظام هي خاصية ثابتة طوبولوجيا تقاوم التغييرات المحلية.

يمكن لأجهزة الكمبيوتر الكمومية في المستقبل الاستفادة من هذا الثبات. يوضح Zaletel ، الذي درس الخصائص الطوبولوجية للسوائل الدورانية ، إذا كانت لديك أربع حالات طوبوغرافية مستقلة عن الاضطرابات أو الأخطاء المحلية ، "سيكون لديك طريقة لتخزين المعلومات الكمية ، حيث قد تشير بتك إلى الحالة التي تكون فيها". أطوار كمومية أخرى. لا تحتاج أنظمة مثل السوائل الدورانية إلى الالتفاف حول الحيد من أجل الحصول على حالات أرضية محمية طبولوجيا. إن صندوق الحماية المفضل للباحثين هو " الرمز الحلقي " ، وهي مرحلة أنشأها نظريًا من قبل منظّر FCC Alexei Kitaev من معهد كاليفورنيا للتكنولوجيا في عام 1997 وتم عرضها في تجارب على مدى السنوات العشر الماضية. يمكن أن يوجد رمز حلقي على متن الطائرة ولا يزال يدعم العديد من الحالات الأساسية المتأصلة في سطح الحيد. في الواقع ، يمكن أن تتحول حلقات الدوران من حافة واحدة من النظام وتظهر على الحافة الأخرى ، والحلقات الملتوية حول النظام تكافئ الحلقات حول فتحة الحيد. قال زاليتل "نحن نعرف كيف نبني روابط بين خصائص الحالة الأرضية للنظام على الحيد والسلوك المقابل للجسيمات".

يمكن أن تكون سوائل السبين في مراحل أخرى ، حيث لا تشكل الس spينات حلقات مغلقة ، ولكنها تتفرع وتشكل شبكة من السلاسل. هذه مرحلة سائلة من شبكة سلسلة ، والتي ، وفقًا لفيينا ، "يمكن أن تقدم النموذج القياسي بالكامل" لفيزياء الجسيمات ، بدءًا من محيط ثلاثي الأبعاد للكيوبتات.

عالم المراحل

أكملت الدراسات التي أجرتها عدة مجموعات في عامي 2009 و 2010 تصنيف المراحل "المعزولة" للمادة التي تتكون في بعد واحد - سلاسل الجسيمات. المرحلة المعزولة هي في الحالة الأرضية: هذه الحالة منخفضة الطاقة بعيدة بما يكفي عن حالات الطاقة العالية بحيث يستقر النظام بشكل مستقر في هذه الحالة. فقط في الأطوار الكمومية المعزولة ، تظهر إثارة مثيرة في شكل جسيمات. المراحل غير المنفصلة هي شوربة الكم الهائلة ، ولا تزال خصائصها في الغالب غير مستكشفة.

بالنسبة لسلسلة البوزونات ذات البعد الواحد - الجسيمات مثل الفوتونات ، مع دوران كمّي صحيح (مما يعني أنها تعود إلى حالتها الأصلية بعد أن تتبادل) ، هناك طوبولوجيا طوبولوجية واحدة فقط معزولة. في هذه المرحلة ، تمت دراستها لأول مرة من قبل منظّر برينستون دنكان هالدين ، الذي حصل على جائزة نوبل لعقود من العمل في المراحل الطوبوغرافية في عام 2016 مع ديفيد ثولس وجون مايكل كوسترليتز ، تنتج سلسلة تدور جزيئات مع نصف عدد صحيح تدور في كلا الطرفين. تحتوي سلسلة الفرميونات على مرحلتين طوبولوجيتين منفصلتين (هذه جزيئات مثل الإلكترونات والكواركات ، مع نصف عدد صحيح يدور - مما يعني أنه عندما يتم تغيير المواقف تصبح حالتها سلبية). لا ينمو الترتيب الطوبولوجي في هذه السلاسل ذات البعد الواحد من التشابك بعيد المدى ، ولكن من التماثل المحلي الذي يربط الجسيمات المجاورة. تسمى هذه المراحل "أطوار طوبوغرافية محمية بشكل متناظر" وتتوافق مع "دورات مجموعات المجموعات المتجانسة" ، وهي أشياء رياضية مرتبطة بمثل هذه الثوابت مثل عدد الثقوب في المجموعة.


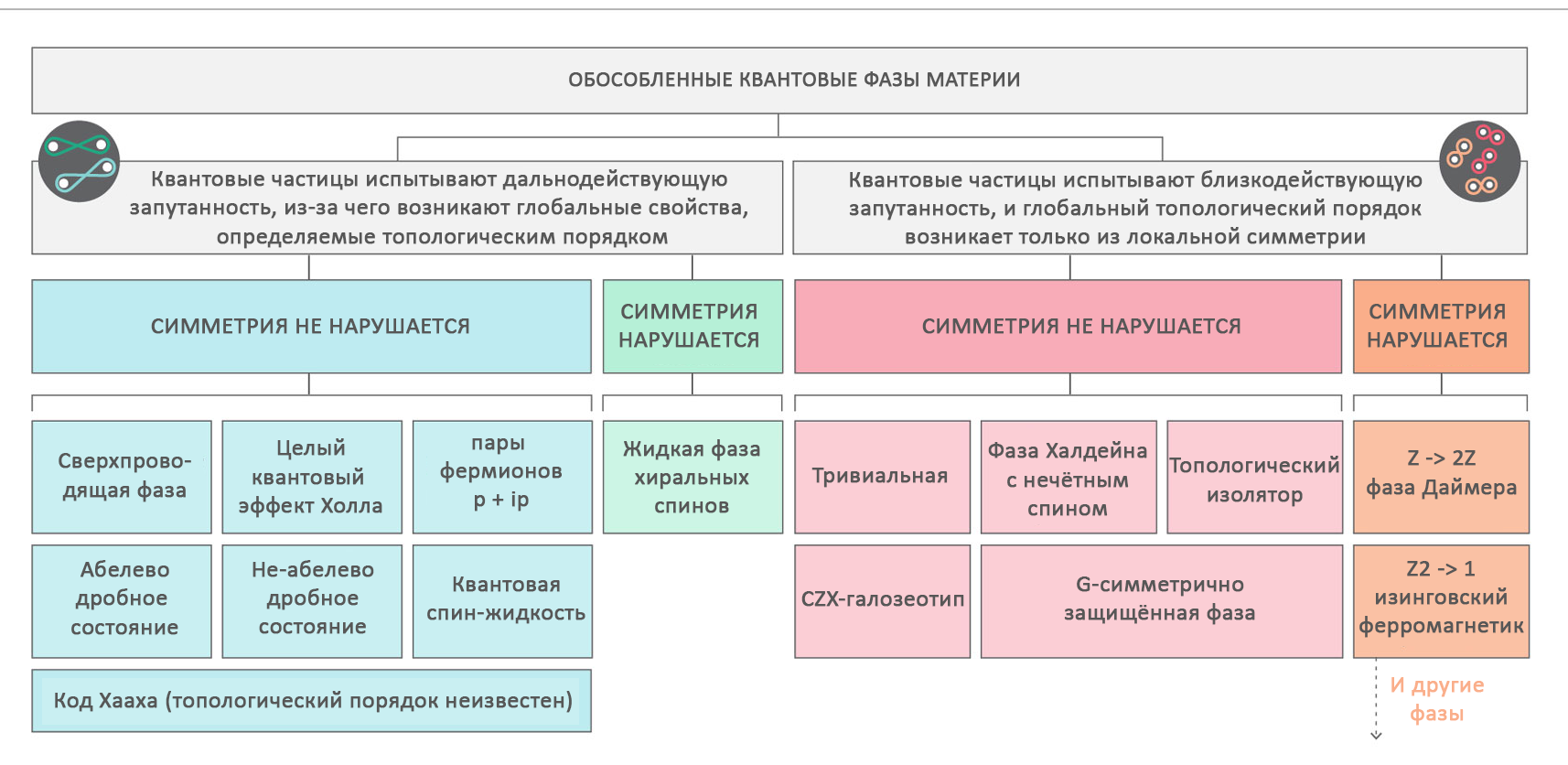الجدول الدوري للمراحل: يوضح الجدول أمثلة نموذجية للمراحل المعزولة ، مع حالة أرضية مستقرة. يعتبر التصنيف كاملاً للمساحات أحادية البعد والثنائية الأبعاد. بالنسبة للمساحات ثلاثية الأبعاد ، لا يُعرف إلا القليل.

المراحل ثنائية الأبعاد أكبر بكثير وأكثر إثارة للاهتمام. قد تظهر ما يعتبره بعض الخبراء الترتيب الطوبولوجي "الحقيقي": الترتيب المرتبط بالتشابك الكمومي بعيد المدى ، مثل تقلبات الحلقة في مائع السبين. على مدى السنوات القليلة الماضية ، أظهر الباحثون أن أنماط التشابك هذه تتوافق مع الهياكل الطوبولوجية التي تسمى فئات الموتر ، وترقيم الطرق المختلفة التي يمكن أن تدمجها الأشياء وتلفها حول بعضها البعض. قال ديفيد بيريز جارسيا من جامعة كومبلوتنسي بمدريد: "فئات Tensor توفر طريقة لوصف الجزيئات التي تدمج وتضفر باستمرار".

يعمل الباحثون ، مثل بيريز جارسيا ، على دليل رياضي على اكتمال الفئات المعروفة جيدًا للمراحل الطوبولوجية المعزولة ثنائية الأبعاد. ساعد في الانتهاء مع فصول أحادية البعد في عام 2010 ، باستخدام الاعتقاد المقبول عمومًا بأن هذه المراحل دائمًا تقريبًا تقريبًا بواسطة نظريات المجال الكمي - الأوصاف الرياضية التي تعتبر فيها البيئة التي توجد فيها الجسيمات الكمومية سلسة. قال بيريز جارسيا: "تغطي فئات الموتر هذه افتراضيًا جميع المراحل ثنائية الأبعاد ، ولكن حتى الآن لا يوجد دليل رياضي دقيق". - بالطبع ، سيكون الأمر أكثر إثارة للاهتمام إذا أمكن إثبات أن هذه ليست كل المراحل. الأشياء الغريبة دائمًا ما تكون أكثر إثارة للاهتمام ، لأنها تحتوي على فيزياء جديدة ، ويمكن أن تكون مفيدة ".

تمثل المراحل الكمومية غير المعزولة مجالًا آخر من إمكانات الدراسة ، ولكنها محاطة بضباب منيع لمعظم الطرق النظرية. يقول سينثيل تودادري ، المنظر في علوم الكمبيوتر من معهد ماساتشوستس للتكنولوجيا: "لا يمكننا التحدث بلغة الجسيمات ، وقد بدأنا نواجه صعوبات خطيرة للغاية". على سبيل المثال ، تعمل المراحل غير المعزولة كعقبة رئيسية أمام فهم الموصلية الفائقة ذات درجة الحرارة العالية. إنها تجعل الحياة صعبة بالنسبة لباحثي الجاذبية الكمومية ، الذين انضموا إلى حركة "جميع الكوبيتات" ، الذين يعتقدون أنه ليس فقط الجسيمات الأولية ، ولكن أيضًا الزمكان والجاذبية ، تظهر بسبب أنماط التشابك الموجودة في المحيطات الكيتية الأساسية. قال بريان سوينجل ، الفيزيائي النظري في جامعة ميريلاند: "نقضي الكثير من الوقت في العمل مع الدول غير المعزولة في" جميع الكوبيتات "لأنه من هناك تأتي الجاذبية - على الأقل هذا ما نعتقده في الوقت الحالي". يحاول بعض الباحثين استخدام المبدأ الرياضي للازدواجية لتحويل صورة حساء الكم إلى وصف مكافئ للجسيمات المصنوعة في بُعد أعلى. يقول تودادري: "ينبغي النظر إلى هذا على أنه استكشاف مناطق جديدة".

يمكن رؤية حماس أكبر للباحثين في الفضاء ثلاثي الأبعاد. حتى الآن ، من الواضح أنه عندما يتم تحرير الدوران والجسيمات من أغلال ثنائية الأبعاد وملء الفضاء ثلاثي الأبعاد للواقع ، تبدأ أنظمة غريبة بشكل لا يمكن تخيله من التشابك الكمي بالظهور. يقول بيريز جارسيا: "حتى الآن ، هناك أشياء في ثلاثة أبعاد تتملص من فئات الموتر". "الإثارة [الحقول] شديدة البرية".

كود هاه

وقد ظهرت أعنف المراحل ثلاثية الأبعاد قبل سبع سنوات.اكتشف خريج موهوب في جامعة كاليفورنيا للتكنولوجيا ، Jeongwan Haah ، ذلك بمحاكاة كمبيوتر عندما كان يبحث عن "رمز الحلم": حالة كمية أساسية موثوقة بما يكفي لتخزين الذاكرة الكمية بأمان حتى في درجة حرارة الغرفة.

لهذا ، كان على Haah أن تتحول إلى ثلاثة أبعاد. في المراحل الطوبولوجية ثنائية الأبعاد ، مثل رمز حلقي ، يتم إدخال نسبة كبيرة من الأخطاء من قبل "عوامل التشغيل الشبيهة بالسلسلة": الاضطرابات في النظام التي تؤدي إلى تشكيل عشوائي لسلاسل الغزل. يمكن لهذه الخيوط في بعض الأحيان أن تقوم بتدوير حلقات جديدة حول فتحة الحيد ، وتغيير عدد الحلقات من الزوجي إلى الغريب والعكس بالعكس ، وتحويل الشفرة الحلقية إلى واحدة من الحالات الكمية الثلاثة الأخرى. نظرًا لأن الخيوط تنمو بشكل لا يمكن السيطرة عليه وتلتف حول كل شيء آخر ، يقول الخبراء أنه في عالم ثنائي الأبعاد لا يمكن بناء ذاكرة كمية جيدة.


Jionwan Haah

كتب Haach خوارزمية بحث ثلاثية المراحل تتجنب عوامل التشغيل الشبيهة بالسلسلة. أصدر الكمبيوتر 17 حلاً دقيقًا ، ثم قام بفحصها يدويًا. تم التأكيد على أن المراحل الأربع خالية من عوامل التشغيل الشبيهة بالسلسلة ؛ أصبحت إحدى المراحل ذات التماثل الأعظم تعرف باسم كود Haach.

من المحتمل أن يكون كود Haah مفيدًا لتخزين الذاكرة الكمية ، ولكنه غريب في نفس الوقت. يتذكر شياو تشين ، وهو منظّر في لجنة الاتصالات الفدرالية من كالتيك ، سماع أخبار عن ذلك كطالب دراسات عليا في عام 2011 ، بعد شهر أو شهرين من اكتشاف هاه المربك. وتقول: "لقد صُدم الجميع". "لم نكن نعرف إذا كان بإمكاننا فعل أي شيء حيال ذلك." واليوم ، استمر هذا الوضع لسنوات عديدة ".

كود Haach على الورق بسيط للغاية: إنه حل لمعادلة طاقة ذات مصطلحين يصفان الدوران المتفاعل مع ثمانية من أقرب جيرانه في شبكة مكعبة. وقال تودادري إن المرحلة الناتجة "تجهد مخيلتنا".

سمة الشفرة هي كيانات تشبه الجسيمات ، وهي كسور ، على عكس أنماط الحلقة في السوائل الشائكة الكمومية ، ليست سائلة وتستقر في مكانها ؛ يمكن للفراكتونات أن تقفز فقط بين مواضعها في الشبكة إذا تمت معاملة هذه المواضع كنمط كسوري. أي ، على سبيل المثال ، من أجل إجبار الفركتونات التي تقف عند رؤوس رؤوس الأسطح على تبادل الأماكن ، من الضروري صب الطاقة في كل قمة من النظام ؛ ولكن إذا قمت بزيادة المقياس ، اتضح أن ما اعتبرناه الذروة يتحول بالفعل إلى القمم الأربعة للرباعي رباعي الأصغر الأصغر ، وعلينا صب الطاقة في كل هذه القمم أيضًا. لا يزال التكبير ، نجد مرة أخرى رباعي الأسطح أصغر ، وهكذا. هذا السلوك الكسوري يعني أن كود Haah لا ينسى أبدًا الشبكة الأساسية ،ولا يمكن تقريبه من خلال وصف سلس للشبكة ، كما هو الحال في نظرية المجال الكمي. علاوة على ذلك ، ينمو عدد الحالات الأرضية لرمز Haach مع حجم الشبكة الشبكية الموجودة في القاعدة - وهذه الخاصية بالتأكيد ليست طوبولوجيا (إذا قمت بتمديد الحيد ، فإنه لا يزال حافزًا).

الحالة الكمية لكود Haach مستقرة للغاية ، حيث من غير المحتمل أن يظهر عامل فركتال مثالي له بشكل عشوائي. يقول الخبراء أن النسخة المنفذة من هذا الرمز يمكن أن تكون ذات أهمية كبيرة من وجهة نظر تقنية.

أثارت مرحلة Haah موجة من التفكير النظري. ساعد Haah في ذلك عندما اكتشف ، في عام 2015 ، مع زميلين من معهد ماساتشوستس للتكنولوجيا (MIT) ، العديد من الأمثلة في فئة المرحلة ، والمعروفة الآن باسم "نماذج fracton" ، والتي تبسط أقارب شفرة Haach. تم تقديم النموذج الأول لهذه العائلة من قبل كلاوديو شامون من جامعة بوسطن في عام 2005. درس تشين وعلماء آخرون طوبولوجيا أنظمة الكسر ، بعضها يسمح للجسيمات بالتحرك على طول الخطوط أو الطائرات في الفضاء ثلاثي الأبعاد ، ونتيجة لذلك يمكنهم المساعدة في الفهم المفاهيمي لما يحدث أو قد يكون أكثر ملاءمة للتنفيذ التجريبي. يقول تشن عن قانون "هاه": "يفتح هذا الطريق أمام العديد من الأشياء الغريبة". - هذا دليل على قلة معرفتنا عن العالم ثلاثي الأبعاد والأبعاد الأعلى.وبما أننا لا نملك حتى الآن صورة منهجية لما يحدث ، فإننا ننتظر الكثير من جميع أنواع الاكتشافات ".

حتى الآن ، لا أحد يعرف إلى أي جزء من المشهد من المراحل المحتملة ينتمي رمز Haach وأقاربه ، أو حجم مساحة الاحتمالات التي قد تكون. ووفقًا لتودري ، فقد حقق المجتمع تقدمًا في تصنيف أبسط مراحل معزولة ثلاثية الأبعاد ، ولكن هناك حاجة إلى مزيد من البحث قبل بدء برنامج التصنيف الكامل. ووفقا له ، من الواضح أنه "عندما نصنف المراحل المعزولة للمادة في الفضاء ثلاثي الأبعاد ، سيتعين علينا مواجهة مثل هذه الاحتمالات الغريبة ، التي اكتشفها هاه لأول مرة".

يعتقد العديد من الباحثين أنه قد تكون هناك حاجة إلى مفاهيم تصنيف جديدة لوصف الطبيعة الكسرية لشفرة Haah واكتشاف الطيف الكامل لإمكانيات المادة الكمية ثلاثية الأبعاد. قال فين: "نحتاج إلى نوع جديد من النظرية ، طريقة جديدة للتفكير". وقال ، ربما ، نحن بحاجة إلى صورة جديدة للمخططات غير السائلة للمشاركة طويلة المدى. وقال "لدينا بعض الأفكار العامة ، ولكن لا توجد رياضيات منهجية لتطبيقها". - لدينا شعور معين كيف يبدو. التنظيم التفصيلي لا يكفي. لكن هذا مثير ".