مرور الزهرة على قرص الشمس وتحديد المسافة بينهما

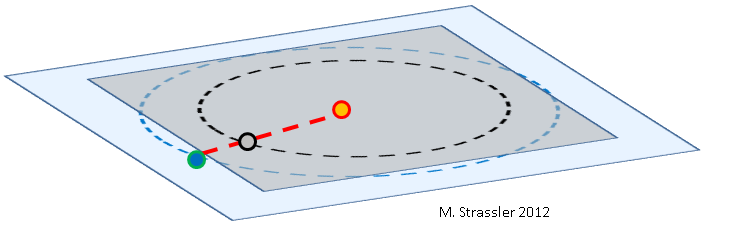
التين. 1: الأرض (الزرقاء) ، والزهرة (الرمادية) ، والشمس (البرتقالي) ، وليس على نطاق واسع.

فيما يتعلق بمرور كوكب الزهرة عبر قرص الشمس في عام 2012 ، تمت كتابة العديد من المقالات بالفعل. حول كيفية حدوث هذا الحدث نادرًا ، ولماذا بالضبط: من الناحية النظرية ، يجب أن يمر الزهرة ، التي تتحرك حول الشمس أكثر من الأرض ، بين الأرض والشمس أثناء كل دورها (الشكل 1) ، ولكن بسبب لم يتم محاذاة مداري كوكبين (ليسا في نفس المستوى ، انظر الشكل 2) ، غالبًا ما يمر كوكب الزهرة فوق أو تحت الشمس من وجهة نظر الأرض.

ولكن بدلاً من تكرار كلمات الآخرين ، أريد أن أضيف بعض التفاصيل التي ليس من السهل العثور عليها على الإنترنت.

ربما قرأت أنه باستخدام تقنية تستند إلى منطق الفلكي إدموند هالي (المذنب الشهير هالي) الذي صنعه من 1678 إلى 1716 ، وكذلك جيمس غريغوري إليه ، تم استخدام مرور فينوس في 1716 لتحديد المسافة من الأرض إلى الشمس (وقبل كوكب الزهرة ، وجميع الكواكب الأخرى) مع خطأ 2 ٪ هي أعلى من تلك التي تحققت في ذلك الوقت. كان من المأمول أن تكون الدقة أعلى بعشر مرات ، ولكن تأثير بصري غير متوقع يسمى " تأثير الهبوط الأسود " تدخل في العملية - لا تزال هناك مناقشات حول الأسباب الدقيقة لحدوثها. ولكن ربما لم تقرأ أن هذا القياس - والعديد من القياسات الأخرى لمسافات في علم الفلك ، حتى النجوم القريبة إلى حد ما - يعتمد على مبدأ المنظر ، على نفس الحقيقة الهندسية التي تستخدمها أعيننا ودماغنا لإدراك العمق ، أو قدرتنا على الشعور كم تبعد الأشياء عنا ببساطة عن طريق النظر إليها.


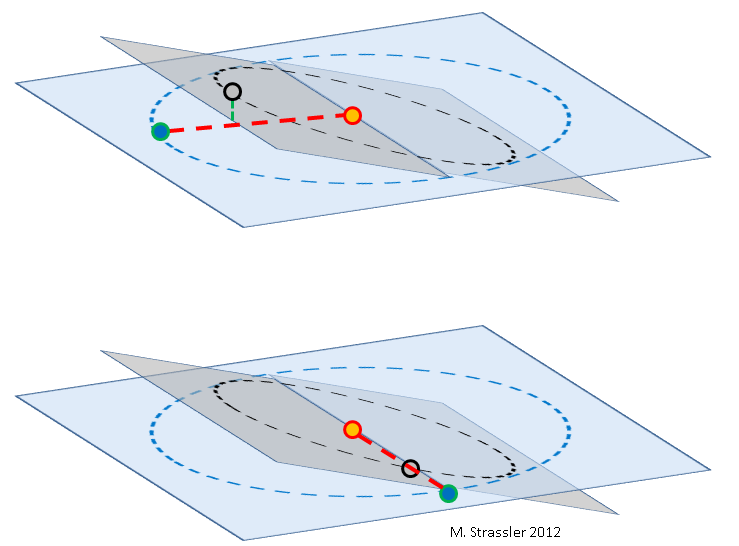التين. 2: الأرض (الزرقاء) والزهرة (الرمادية) والشمس (البرتقالية) ، وليس على نطاق واسع. يميل مدار الزهرة (دائرة سوداء في مستطيل رمادي) بالنسبة إلى مدار الأرض (دائرة زرقاء في مستطيل أزرق). إن درجة الإمالة مبالغ فيها إلى حد كبير. نظرًا لأن الأرض والزهرة تدور حول الشمس بسرعات مختلفة ، فيمكنهما تمرير بعضهما البعض في أي نقطة في المدارات.

أعلى: خلال هذا المقطع ، يقع الزهرة فوق أو أسفل (الخط الأخضر) الخط الذي يربط الأرض والشمس (الخط الأحمر) ، لذلك لا يمر الزهرة عبر القرص الشمسي.

أدناه: في حالات نادرة ، يتزامن الخط الذي يربط الأرض والشمس مع خط تقاطع طائرات المدارات ، ويقع كوكب الزهرة بالقرب من نفس الخط ، مما يؤدي إلى المرور.

بدون اختلاف المنظر ، من السهل أيضًا تحديد المسافة النسبية من كوكب الزهرة إلى الشمس - أي نسبة نصف قطر مدار فينوس L _V إلى نصف قطر مدار الأرض L _E. لذلك ، في علم الفلك في عصر النهضة ، تم حساب المسافات النسبية من الكواكب إلى الأرض والشمس في وقت مبكر جدًا. ولكن من أجل تحديد L _V و L _E بشكل منفصل ، من الضروري قياس اختلاف المنظر ، ويمكن لمرور الزهرة توفيره. أعطى مرور كوكب الزهرة في ستينيات القرن التاسع عشر قياسًا دقيقًا إلى حد ما لـ L _E - L _V ، المسافة "المطلقة" من الأرض إلى الزهرة. هذا جعل من الممكن معرفة L _E ، L _V ، والمسافات إلى جميع الكواكب الأخرى مع خطأ بنسبة اثنين في المئة. قبل ذلك ، في نهاية القرن السابع عشر ، تم إجراء قياس للمسافة من الأرض إلى المريخ ، والتي كان خطأها حوالي 10 ٪ ؛ لقد كان أيضًا مستندًا إلى اختلاف المنظر ، لكن هذه قصة مختلفة تمامًا.

ملاحظة أولية: الأرض والزهرة ، وحتى الشمس صغيرة جدًا مقارنة بالمسافات بينهما ، لذلك يكاد يكون من المستحيل رسم صور دقيقة. في الرسوم التوضيحية ، يجب عليك دائمًا رسم كواكب أكبر مما هي عليه بالفعل ، فيما يتعلق بالمسافات بينها ، حتى تتمكن من فهم المفهوم. ضع هذا في الاعتبار! جميع الرسوم التوضيحية الخاصة بي ليست مرسومة على نطاق واسع.

الأحجام النسبية لمداري فينوس والأرض

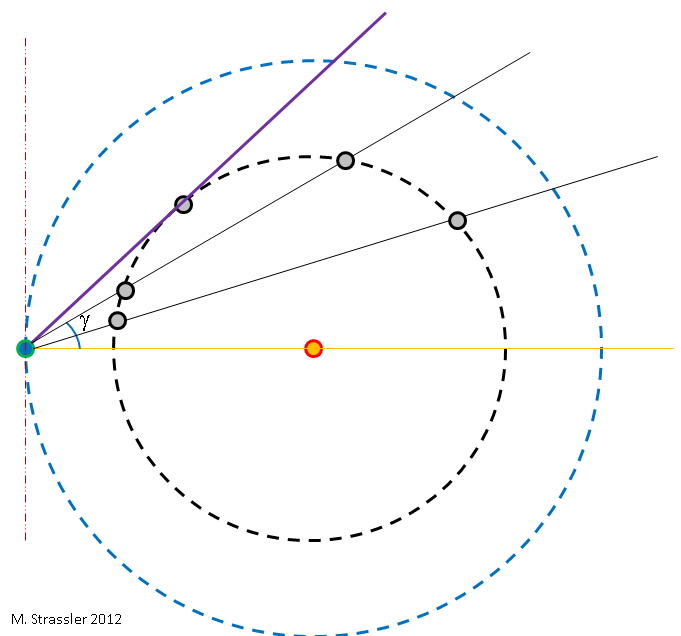
التين. 3

لفهم السبب الرئيسي لبساطة تحديد L _V / L _E ، افترض أن مداري الأرض والزهرة دائريان ومحاذاة - يقعان في نفس المستوى (كما هو موضح في الشكل 1 ، متساوي القياس ، وفي الشكل 3 هو "منظر علوي"). في الواقع ، مدارات الأرض والزهرة ممدود قليلاً وغير محاذاة (الشكل 2). لكن الاهتزازية وعدم تطابق الطائرات ليسا مهمين جدًا في تفكيرنا ، لذا يمكننا أولاً تجاهلها ، ثم تذكر مرة أخرى للحصول على إجابات أكثر دقة.

سنقوم هنا بتطبيق التكنولوجيا الكلاسيكية للفيزياء: سنقوم بعمل تقريب كافٍ للمهمة الحالية ولن نتعمق أكثر من اللازم. هذه طريقة قوية جدًا للتفكير في العلوم والمعرفة بشكل عام - فهي كافية للإجابة على أي سؤال بمستوى معين من الدقة ، بحيث يمكنك استخدام أبسط تقنية من تلك التي ستمنحك المستوى المطلوب من الدقة. تم استخدام هذه الطريقة بشكل مثالي لقرون وهي قابلة للتطبيق ليس فقط على الفيزياء.

لذلك ، سنأخذ التقريب الذي تكون فيه المدارات دائرية ومحاذاة ، وسوف نتلقى الإجابات الصحيحة تقريبًا ، مع خطأ بنسبة قليلة في المئة. سيكون هذا كافياً لتوضيح المفاهيم الأساسية التي أسعى إليها. صدقني ، يمكنك إجراء حسابات أكثر دقة - أو يمكنك أن تصبح خبيرًا في هذا الأمر بنفسك. لكن تقريبنا لن يعطي إجابة جيدة جدًا فحسب ، بل سيكون قادرًا أيضًا على إظهار سبب سهولة حساب نسبة L _V إلى L _E ، ولكن ليس قيم L _V و L _E نفسها.

خلال العام الذي تدور فيه الأرض والزهرة حول الشمس بسرعات مختلفة ، يتغير الوضع النسبي للأرض والزهرة فيما يتعلق بالشمس. إذا قررت في يوم معين (يوم ، شهر ، سنة) أن أرسم صورة مع الشمس في الوسط والأرض على اليسار ، كما في الشكل. 2 ، ثم يمكن أن يكون فينوس في أي مكان في مداره. هذا يعني أنه من وجهة نظر الأرض ، ستتغير الزاوية بين الزهرة والشمس في السماء اعتمادًا على التاريخ. هذا مبين في الشكل. 3 ، حيث تسمى الزاوية γ. الزاوية سهلة القياس ؛ العثور على الزهرة في السماء بعد غروب الشمس أو قبل شروق الشمس وقياس الزاوية بين الزهرة والشمس ؛ انظر الصورة 4.


التين. 4

من الشكل. يوضح الشكل 3 أن γ لها حجم أقصى - الزاوية بين الخطين البرتقالي والأرجواني. عند الانتقال إلى المدار ، ستظهر الزهرة في مكان آخر مع كل غروب شمس ؛ لبعض الوقت سوف يرتفع أعلى من الأفق لعدة ليالٍ متتالية ، ثم يبدأ تدريجياً في الظهور أدناه. بمراقبة الزهرة لعدة ليالٍ متتالية وقياس γ ، يمكننا تحديد القيمة القصوى لـ γ ، والتي سأطلق عليها γ _max .

من الشكل. 3 من الواضح أنه (كما هو موضح في الشكل 4) γ _{كحد أقصى} أقل من 90 درجة ، حيث يجب أن يقع الخط البنفسجي بين البرتقالي والأحمر عموديًا. هندسيًا ، هذا نتيجة لحقيقة أن كوكب الزهرة دائمًا ما يكون أقرب إلى الشمس من الأرض. تشرح هذه الزوايا لماذا تكون الزهرة مرئية دائمًا إما مباشرة بعد غروب الشمس أو قبل الفجر (باستثناء الأيام التي تكون فيها خلف الشمس). لا يمكن أن تكون الزهرة في أوجها بعد حلول الظلام ، لأنها يجب أن تكون على يسار الخط الأحمر.


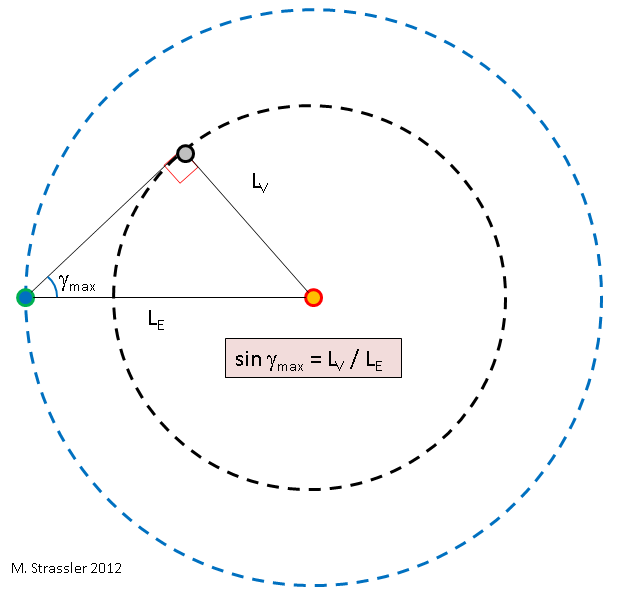التين. 5

يمكننا الآن تحديد نسبة نصف قطر مدارين - L _V إلى L _E - باستخدام γ _max . هذا هو أبسط الهندسة ، انظر الشكل. 5. الخلاصة هي أنه عندما تكون الزهرة في أقصى زاوية من الشمس ، فإن الخط بين الشمس والزهرة يكون متعامدًا مع الخط الفاصل بين الأرض والزهرة ، وبالتالي فإن الخطوط التي تربط هذه الأجسام الثلاثة تشكل مثلثًا قائمًا. من هنا نحصل على استخدام علم المثلثات القياسي:

$$

$$L_V / L_E = \ gamma_ {max}$$

ومن هنا ، بمساعدة صيغ هندسية بسيطة أخرى ، نحصل على العلاقة بين المسافات إلى الكواكب الأخرى.

هذا ليس دقيقًا تمامًا ، للأسباب الموضحة في البداية ؛ مدارات الكواكب عبارة عن قطع ناقصة ، ولا تستلقي على سطح الماء. وبعبارة أخرى ، لا _يتم تخزين L _V و L _E خلال العام ، ويتم تطبيق γ _max بشكل أكثر تعقيدًا قليلاً ، في ثلاثة أبعاد ، كما هو الحال في الشكل. 2 ، ولكن ليس في اثنين ، كما في الشكل. 1 و 3 و 5. ولكن بمساعدة القياسات الدقيقة لموضع الزهرة والشمس في السماء ، من الممكن تحديد المدار الدقيق لكوكب الزهرة والأرض حول الشمس وتحسين الحسابات. المعنى هو نفسه ؛ جميع القياسات لموضع الزهرة والشمس في السماء تسمح لنا فقط بقياس الأحجام النسبية لمداري الزهرة والأرض. ولكن لا يمكن تحديد القيم الدقيقة لـ L _V و L _E بهذه الطريقة. نحن هنا بحاجة إلى نهج مختلف.

مرور الزهرة ، اختلاف المنظر والمسافة إلى الشمس

السبب في أن مرور فينوس يسمح لك بقياس القيم المطلقة لمداري الأرض والزهرة هو أنه يمكن ملاحظة هذه العملية بدقة عالية من أماكن مختلفة على الكرة الأرضية ، ونتيجة لذلك سيكون لديك منظورين للموقع المرئي للزهرة فيما يتعلق بالشمس ، مقاسة من أماكن مختلفة مع معروفة المسافة بينهما. يتيح لك قياس اختلاف المنظر تحديد القيمة المطلقة للمسافة من الأرض إلى الزهرة من زاوية الاختلاف والمسافة بين نقطتي قياس على الأرض - تمامًا مثل نوع مختلف من الأجسام للعين اليسرى واليمنى يسمح لدماغنا بإعطائنا إحساسًا بالعمق - شعور بالمسافة من الأشياء.


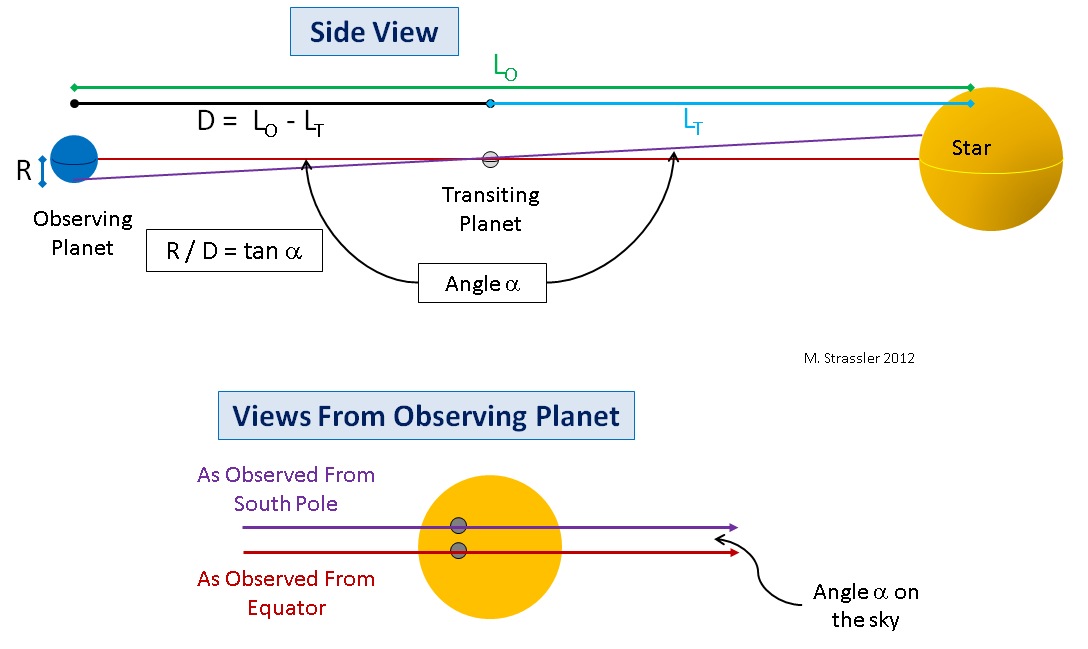
التين. 6

من أجل عرض توضيحي ، دعوني أرسم كيف ستبدو من كوكب كبير. في الشكل. يوضح الشكل 6 الكوكب الذي سنراقب به الممر (ستكون الأرض) والكوكب الذي يمر أمام النجم (سيكون كوكب الزهرة). سأقدم حالة مبسطة (فقط لجعل الهندسة أبسط والمفهوم الرئيسي أسهل للرؤية) ، حيث يتم محاذاة الكواكب والنجم ، لذلك من وجهة نظر المراقب عند خط الاستواء ، سيمر كوكب يمر على طول خط الاستواء للنجم. أعلاه في الشكل. يظهر 6 منظر جانبي. لاحظ الخط الأحمر من خط الاستواء لكوكب المراقبة إلى النجم من خلال خط استواء الكوكب الذي يمر عبر قرص النجم.

في حالة المحاذاة المثالية ، سيرى المراقب عند خط الاستواء للكوكب الخارجي كيف يمر الكوكب الداخلي على طول خط الاستواء للنجم. يظهر هذا كخط أحمر في أسفل الشكل. 6. لكن المراقب من القطب الجنوبي للكوكب الخارجي سيرى كيف يمر الكوكب الداخلي بالنجم على طول المسار (الخط الأرجواني) شمال خط الاستواء للنجم (في حالة القطب الشمالي ، سيكون كل شيء بالعكس). إذا قمنا بقياس الزاوية α في السماء بين المسارات التي يتحرك على طولها كوكب عابر ومعرفة نصف القطر R لكوكب المراقبة ، يمكننا رسم مثلث قائم الزاوية يربط الكوكب العابر ومركز كوكب الرصد وقطب كوكب المراقبة بزاوية صغيرة؟ علم المثلثات البسيط سيعطينا المسافة D بين الكواكب أثناء المرور ، أين

$$

$$D = R / tan \؛ \ alpha$$

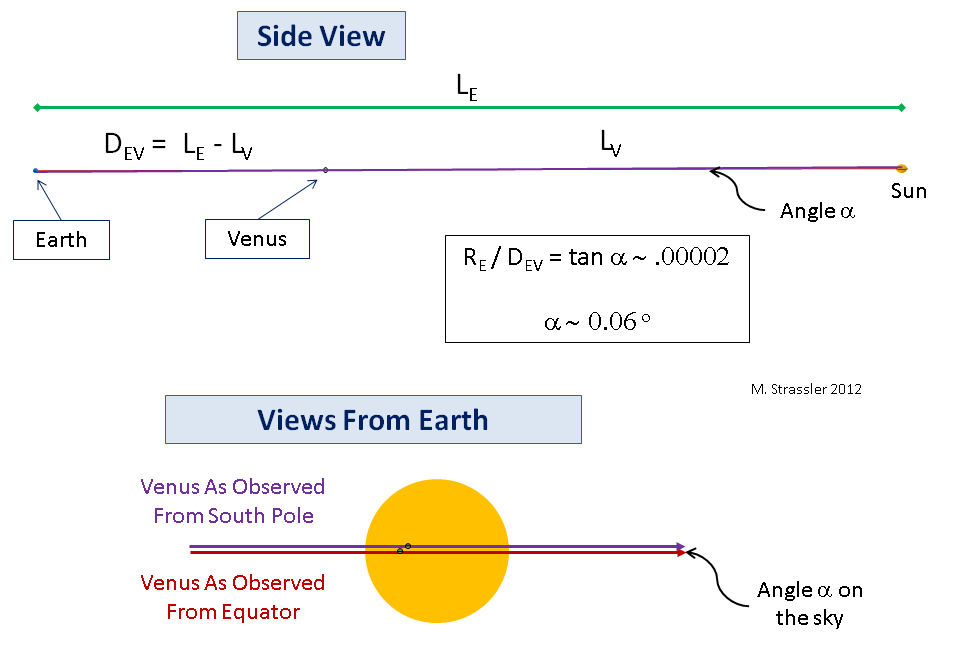
التين. 7

وينطبق الشيء نفسه على الأرض والزهرة والشمس ، باستثناء أن الأرض والزهرة صغيرة جدًا مقارنة بالمسافة بينهما والشمس بحيث تكون الزاوية α تساوي حوالي 1/20 درجة! (هذه كمية صغيرة نوعًا ما ، ولكنها قابلة للقياس تمامًا ، على الرغم من أن القياس الدقيق للمسافة إلى الشمس ، التي أراد علماء الفلك في القرن الثامن عشر الحصول عليها ، يتطلب قياسًا دقيقًا من الناحية الفنية المعقدة لحجم زاوية صغيرة). لن أرسم مثل هذه الزاوية الصغيرة ، لذلك عليك أن تأخذ كلمتي لأن ما يحدث هو نسخة مما صورته في الشكل. 6 ، مع الكواكب ونجم (الشمس) أصغر بكثير من رسمها هناك ، فيما يتعلق بالمسافات. حتى الصورة في الشكل. 7 يجعل الكواكب أكبر بكثير مما هي عليه. لكن الفكرة لم تتغير: المسافة D _EV بين الأرض والزهرة أثناء المرور يمكن تحديدها بقياس زاوية المنظر α (الجزء السفلي من الشكل 7 ؛ لاحظ أن القطر الزاوي للشمس حوالي 1/2 درجة).

ومع ذلك ، لا يزال هناك العديد من الأسئلة:

• أخبرت كيف تقيس D _EV ، المسافة من الأرض إلى الزهرة خلال الممر. لكن لم يكن هدفنا قياس L _E و L _V ، المسافة من الأرض إلى الشمس ومن الزهرة إلى الشمس؟
• لم يذهب أحد إلى القطب الجنوبي للأرض لمراقبة مرور كوكب الزهرة في عام 1761 أو 1769.
• لقد افترضت أن مدارات محاذاة تمامًا للأرض ، والزهرة وموقع الشمس ، بحيث يمكن للمرء أن يرى كوكبًا من كوكب الزهرة يتحرك على طول خط الاستواء من نقطة على خط الاستواء. لكن هذا ليس هو الحال في الواقع ، وحتى لا يبدو كإجراء نموذجي (وفي عام 2012 لم يكن هذا أيضًا).
• الزاوية α صغيرة بما يكفي ليتم قياسها بدقة - خاصة في الأيام التي سبقت التصوير الفوتوغرافي والرسائل الفورية ، في غياب مؤشرات واضحة لموقع القطب الشمالي للشمس ، مما يجعل من الصعب مقارنة قياسات مسار الزهرة بدقة من نقطتين مختلفتين على الأرض. ومع ذلك ، كان الهدف الأساسي هو قياس الزاوية بما لا يزيد عن جزء واحد من أصل 500 (0.2٪) (على الرغم من تأثير السقوط الأسود ، كانت النتيجة أقرب إلى جزء واحد من 50 (2٪)).

كيف تتعامل مع هذه المشاكل؟

أولاً ، كيف يمكنك الانتقال من قياس D _EV إلى قياس القيم المطلوبة ، L _E و L _V ؟ الأمر بسيط - نحن نعلم بالفعل جميع العلاقات ، على وجه الخصوص ، نحن نعلم بالفعل L _E / L _V (تقريبًا ، من الشكل 4 ، أو ، إذا تناولنا المشكلة بعناية أكبر ، يمكننا حسابها بدقة أكبر) من الزاوية القصوى γ _ماكس بين الزهرة و الشمس من وجهة نظر الأرض. نعلم أيضًا D _EV = L _E - L _V = L _E (1 - L _V / L _E ) من الشكل. 7. لذلك ، يمكننا الحصول على قيمة تقريبية لـ L _E باستخدام:

$$

$$L_E = D_ {EV} / (1 - L_V / L_E) = R / tan \؛ α / (1 - sin \؛ \ gamma_ {max})$$

حيث α هي زاوية المنظر المقاسة أثناء العبور ، و transit _max هي الزاوية القصوى بين الزهرة والشمس (الشكل 5). تتطلب القياسات الأكثر دقة هندسة أكثر تعقيدًا ، ولكن بنفس الفكرة الأساسية.

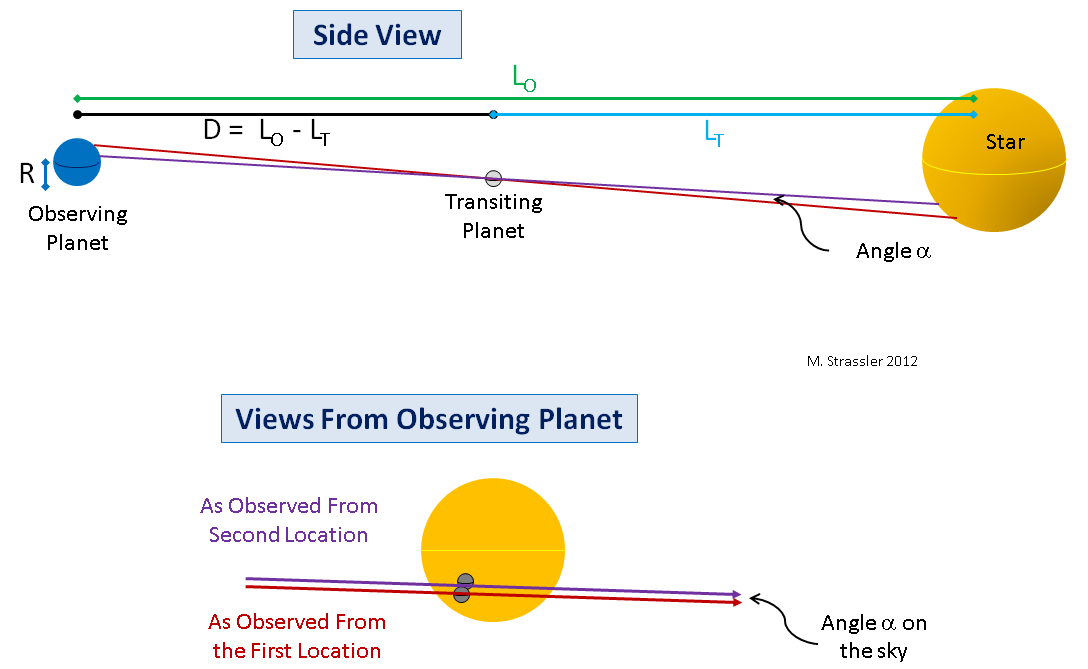
ثانيًا ، حتى إذا كانت مدارات الكواكب متوازنة تمامًا ، فلا يلزم قياس بعدين لمسار الزهرة من خط الاستواء وقطب الأرض. يمكن قياسها من أي خط عرض. تصبح الهندسة أكثر تعقيدًا بعض الشيء ، ولكن ليس كثيرًا ، ولكن يبقى المبدأ (انظر الشكل 8).


التين. 8

ثالثًا ، حتى بدون محاذاة مثالية ، ستظهر زاوية اختلاف صغير عند قياس القيم من نقطتين مختلفتين من الأرض ، وإذا تم قياس هذه الزاوية جيدًا ، يمكن تحويل هذا القياس (من خلال معادلات أكثر تعقيدًا قليلاً) إلى قياس D. يظهر هذا في الشكل. 8 ، لأسفل.

السؤال الرابع هو المشكلة المعقدة تاريخيًا لقياس التحول الزاوي لمسار الزهرة أثناء المرور عبر الزاوية α يقودنا إلى محاولة بديلة لقياس الوقت - إما وقت السفر ، أو ببساطة بداية ونهاية الممر ، وليس الزوايا. تم اقتراح الخيار الأول من قبل هالي بناءً على أفكار غريغوري ، والثاني ، كتحسين إضافي ، تم اقتراحه من قبل جوزيف نيكولا دليلي . لم تتطلب طريقة هالي التزامن على مدار الساعة في أماكن مختلفة من الأرض ؛ لذلك ، كانت طريقة Delil المطلوبة تعتمد على تقنية الساعات الأكثر تقدمًا.

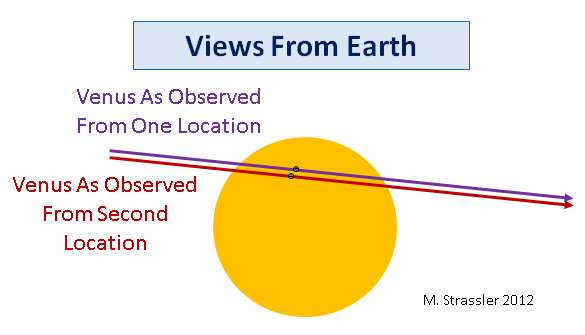
حتى في القرن السابع عشر أو الثامن عشر ، من الأسهل بكثير قياس الفاصل الزمني بدقة ، أو لحظات بداية ونهاية الكسوف ، من القياس الدقيق لموقع الزهرة بالنسبة لقرص الشمس ، خاصة في غياب التصوير الفوتوغرافي. في الشكل. يوضح الشكل 9 أن المسارين البنفسجي والحمري لعبور الزهرة للشمس لهما أطوال مختلفة قليلاً لأنهما لا يعبرانه في مكان واحد ، مما يعني أن مدة المرور ستختلف حسب الوقت المرتبط بزاوية المنظر. لسوء الحظ ، اتضح أن كل شيء أكثر تعقيدًا مما يبدو للوهلة الأولى - تدور الأرض وتتحرك حول الشمس ، لذلك يسافر المراقب مسافة كبيرة إلى حد ما أثناء مرور الزهرة عبر قرص الشمس. لذلك ، هناك حاجة إلى الكثير من الجهد (الحسابات معقدة للغاية ، على الرغم من أن أجهزة الكمبيوتر الحديثة تكون أبسط بكثير) لتحديد الفرق في الفترات الزمنية لبداية ونهاية المقطع الذي لاحظه مراقبان مختلفان على الأرض ، اعتمادًا على المسافة إلى الشمس.

لقد فهم هالي في بداية القرن الثامن عشر جميع المبادئ الهندسية اللازمة (إذا قمت بطرح العبارات الإنجليزية القديمة وأسلوبها من نصوصه ، فستفاجأ بمدى حديث عباراته المعقدة ، وسوف ترى أن العلماء قبل ثلاثمائة سنة كانوا متشابهين جدًا مع علماء اليوم ، يمتلك نفس الذكاء ويفتقر فقط إلى التكنولوجيا العلمية اليوم).


التين. 9

كل هذا يشير إلى أن المنظر - الاختلاف في الموضع المرئي المنسوب إلى الزهرة فيما يتعلق بالشمس من وجهة نظر المراقبين الذين يقيسونها في نفس الوقت ولكن من أماكن مختلفة على الأرض - كان تاريخًا طريقة مهمة جدًا تحديد حجم النظام الشمسي. تتوفر اليوم طرق أكثر قوة لنا ، ولكن قد تكون مهتمًا بحقيقة أن ما تراه اليوم في السماء له أهمية تاريخية كبيرة ، أو يمكنك ببساطة الاستمتاع بمنظر كوكب الزهرة ، وهو يتحرك بشكل مهيب حول نجمنا.