
لذلك أنت مبرمج. لماذا تحتاج حتى كثيرات الحدود؟ على سبيل المثال ، إذن ، إنه طين هندسي جيد ، يمكنك من خلاله تشكيل أشياء مختلفة.
من
مقالتنا التي تشرح جوهر التحليل الرياضي باستخدام الثعبان والدم والديناميت كمثال ، يمكن ملاحظة أنه يمكنك تحليل وتوليف الوظائف التعسفية مثل كثيرات الحدود. ومع ذلك ، ليس من الضروري العمل بشكل خاص مع الوظائف. في بعض الأحيان ، قد تحتاج إلى وضع نموذج لخط من عدة نقاط أو خصائص ، مثل ظلل المنحنيات. على سبيل المثال ، تحتاج إلى عمل نوع من الرسوم المتحركة ، أو تأثير فيديو جميل ، أو رسم منحنى يمر عبر نقاط معينة ، أو إنشاء سطح مستو في مكان ما ومنحني في مكان آخر.
قد لا تكون كثيرات الحدود ، بما في ذلك حتى الخطية ، دائمًا أفضل أداة لهذه المهمة ، ولكنها تمتلك بعض الميزات التي يقدرها المبرمجون حقًا. فهي بسيطة ومتنوعة في طبيعتها ، والأهم من ذلك أنها فعالة للغاية من حيث الأداء. خذ على سبيل المثال كثيرات الحدود التالية:
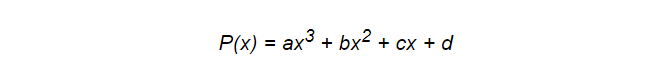
لحساب ذلك ، مطلوب فقط 6 إجراءات الضرب و 3 إضافات. هذا مهم لأن نموذجك سيخضع باستمرار للحساب. ولكن هنا يمكننا إجراء التحسين. سيساعدنا مخطط هورنر في ذلك. بمساعدتها ، يمكن كتابة نفس كثير الحدود كما

وهذا فقط 3 ضربات و 3 إضافات. كما تعلمون ، لقد بدأنا للتو ، وتعلمت بالفعل التخلص من ثلث الحسابات.
الاستيفاء متعدد الحدود
تسمى مهمة تكييف كثيرات الحدود من الدرجة
n إلى نقاط
n + 1 في الفضاء الاستيفاء متعدد الحدود. هناك عدة طرق لتنفيذه. يمكنك استخدام صيغ الاستيفاء
نيوتن أو
لاغرانج ، ولكن أسهل طريقة للحصول على كثير الاستكمال الداخلي هو حل نظام المعادلات الخطية.
إذا مر كثير الحدود من خلال نقطة ، فمن الواضح أننا يمكن أن نقول أن
P (xi) = yi . افترض أننا نريد تكييف كثيرات الحدود لمجموعة من ثلاث نقاط. هذا يعني أن:

في الحالة العامة ، لا يمكننا رسم خط من خلال ثلاث نقاط تعسفية. وعلينا ثنيها ، لتشكيل القطع المكافئ. أو بعبارة أخرى ، أدخل كثيرات الحدود من الدرجة الثانية ، والمعروفة أيضًا بالوظيفة التربيعية.

نظرًا لأن xs و ys معروفان ، فنحن بحاجة فقط إلى حل النظام ومعرفة المعاملات a ، b ، c ، وبما أن هذا النظام يتكون من ثلاث معادلات وثلاثة متغيرات ، يمكننا عادةً الحصول على حل واحد.
للتأكد من ذلك ، حاول تحريك موضع النقاط الثلاث في الرسم البياني السفلي وانظر ماذا سيحدث.

هذا الرسم البياني مفيد جدًا أيضًا في التحليل العقلي للأنظمة الخطية. في الحالة العامة ، من المستحيل احتواء خط مستقيم بثلاث نقاط ، تمامًا كما أنه من المستحيل إيجاد حل لنظام المعادلات n مع المتغيرات غير المعروفة n-1. ولكن في بعض الأحيان يكون ذلك ممكنًا. على سبيل المثال ، في الحالات التي تتطابق فيها بعض النقاط أو تقع جميعها عن قصد على خط مستقيم واحد.
الوضع العكسي أكثر إثارة للاهتمام. يمكننا رسم عدد لا نهائي من القطع المكافئة من خلال نقطتين معينتين. جميعها مناسبة بالتساوي كحل للمشكلة. وفي الوقت نفسه ، لا يمكننا الحصول على حل أفضل بشكل فريد لأنظمة معادلات n ومتغيرات n + 1.
ولكن ماذا لو كان لا يزال ممكناً؟ ماذا لو استطعنا إدخال بعض المعايير الإضافية لاختيار الخيار الأنسب؟
التوليف
تقودنا أسئلة مماثلة إلى منطقة التوليف متعدد الحدود. في حالتنا ، هذا تقاطع بين سلسلة كثيرة الحدود والاستكمال متعدد الحدود. بمساعدة المتسلسلة ، يمكننا نمذجة دالة بناءً على مشتقاتها في وقت ما ، وبمساعدة التوليف ، يمكننا استخدام كل من النقاط والمشتقات (وليس فقط ، ولكن أكثر من ذلك في وقت آخر).
يرتبط مشتق التابع ارتباطًا وثيقًا بالخصائص الهندسية للرسم البياني. المشتق الأول يحدد المماس المنحدر للمماس ، والثاني يحدد الانحناء.
افترض أننا بحاجة إلى تعريف دالة تمر عبر نقطتين ، مع العلم بظلها عند كلتا النقطتين. في هذه الحالة ، يمكننا توليفها بسهولة على أنها كثيرة الحدود.
كما كان من قبل ، نحتاج إلى كتابة نظام المعادلات. الآن نحن بحاجة إلى أربعة شروط ، لذلك يجب أن نختار كثير الحدود من الدرجة 3 ، أي دالة مكعبة.
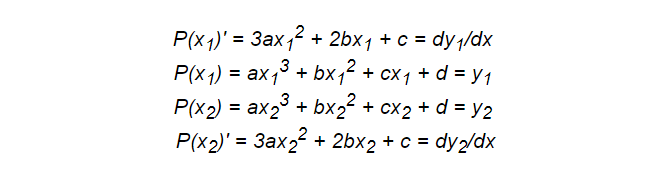
بعض المعادلات مبنية على نقاط والبعض الآخر مشتقات. يمكن أيضًا إضافة التكاملات هنا لتقديم الخصائص الصحيحة اللازمة ، مما يجعل هذه التقنية فعالة جدًا.
ولكننا سنستمر في النظر في وظيفة تربط بين نقطتين من خط سلس مستمر مع قيود عرضية عند هذه النقاط.


ظاهرة رونج
الاستكمال متعدد الحدود له خاصية غير سارة ، والتي تتجلى في زيادة نمو التذبذبات في طرفي الفاصل الزمني مع زيادة في عدد النقاط. تسمى هذه الظاهرة ظاهرة رونج. يحد من إمكانية استخدام الاستكمالات متعددة الحدود البسيطة.
عيب آخر لهذا النهج هو طبيعته العالمية ، أي تغيير في الوظيفة بأكملها مع أدنى تغيير في موقف نقطة واحدة على الأقل. وبالاقتران مع التذبذبات ، تكون النتيجة هي الفوضى.

عقد Chebyshev
تتمثل إحدى طرق مكافحة الفوضى في تحديد شبكة خاصة للاستيفاء -
عقد Chebyshev . هذه قيم س خاصة يتم الحصول عليها عن طريق قسمة نصف دائرة نصف قطرها 1 إلى أجزاء متساوية وإسقاطها على المحور س.
بشكل عام ، يتم إخفاء سحر رياضي معين في هذه التقنية ، ولكن من وجهة نظر براغماتية ، فإنه يهدف إلى تقليل ظاهرة Runge. وعلى الرغم من أنها لا تسمح بجعل الاستيفاء متوقعًا تمامًا ، فإن كل شيء يعمل بثبات على الفاصل الزمني (-1: 1).

بالطبع ، يمكنك تمديد الفاصل الزمني على طول المحور X بقدر ما تحتاجه باستخدام تحويل التلامس أحادي البعد. ليس من الضروري الالتزام بالجزء
(-1؛ 1) .
لكن الاستيفاء في نفس الوقت يحتفظ في كل مكان. لا يزال تغيير النقطة الأولى يؤثر على تشغيل الوظيفة بالقرب من الأخيرة ، على الرغم من أنه ليس بشكل كبير.
المفاتيح
هناك عدد غير قليل من أنواع المفاتيح ، ولكن جميعها موحدة بواسطة سيناريو تطبيق واحد. بمجرد أن يصبح الاستيفاء العالمي لسبب ما مناسبًا لمهامنا ، يمكننا تقسيم فاصلنا الزمني إلى أجزاء أصغر وتحديد الوظائف الفردية للاستيفاء في كل منها.
الشيء الوحيد الذي نحتاج إلى النظر فيه هو الحاجة إلى ربطها في النهايات للحفاظ على الاستمرارية. إذا كنا نضمن استمرارية الوظيفة النهائية المحددة بشكل مجزأ ، ولكن أيضًا مشتقها الأول ، في هذه الحالة ، ستتزامن ظل كل مقطع من شرائحها ، وسيبدو جدولها سلسًا.
يوجد
تصنيف معين للخطوط. على سبيل المثال ، خذ خطًا متعدد الحدود يتكون من جزأين. إذا تم تحديد كل جزء منه من كثيرات الحدود من الدرجة الثالثة ، فإنه يسمى مكعب. قد تمتلك ، على سبيل المثال ، خاصية مثل استمرارية المشتق الأول ، حيث تتطابق المماس عند تقاطع الشظايا. شظاياها ليست متساوية العرض. إنه ليس من أصل طبيعي ، حيث يمكننا السيطرة على المشتقات في نهايته. وبالطبع ، هذا هو استيفاء ، لأنه يمر بالضبط عبر نقاط الشبكة التي أشرنا إليها.

الخلاصة
احتمال أن تضطر إلى تنفيذ عملية الاستيفاء الخاصة بك ضئيل للغاية. هناك العديد من الحلول الجاهزة وفي معظم الحالات ستحتاج فقط إلى اختيار الأداة المناسبة للوظيفة. هذا المجال من المعرفة ليس معقدًا للغاية ، ولكن عدد الكلمات والأسماء غير المعروفة يمكن أن يبتعد.
كان الغرض من هذا الدليل هو تزويدك بفهم أساسي للأفكار المستخدمة للعمل مع كثيرات الحدود والخطوات. لا يتظاهر بأي حال من الأحوال بأنه مكتمل ، لأنه في الواقع ، تتم كتابة كتب كاملة على كل فصل من فصول هذه المادة الصغيرة. ولكننا نأمل ، على الأقل ، أن يكون النهج التفاعلي للعرض التقديمي في هذه المادة مفيدًا ليس فقط لمقدمة موجزة ، ولكن إذا ظهرت مثل هذه الحاجة ، فسوف تساعدك على إتقان الموضوعات الأكثر تقدمًا.
