علم الكونيات - ستانفورد. الملخص. المحاضرة 1

تفتح هذه المقالة سلسلة من محاضرات حول علم الكونيات في جامعة ستانفورد. المحاضرات نفسها باللغة الإنجليزية متوفرة في: Cosmology (2013) - Leonard Susskind - جامعة ستانفورد . شاهدت محاضرة الفيديو وعرضت بسرور. يشرح المحاضر ليونارد ساسكيند سهولة الوصول إليه وممتعة. من الواضح أنه شخص موهوب ومعلم ممتاز.

تشتهر جامعة ستانفورد أيضًا بحقيقة أن مواطننا المتميز أندريه ليندي يعمل هناك ، والذي ربما سيحصل قريبًا على جائزة نوبل في الفيزياء لمساهمته في علم الكونيات الحديث. من يهتم ، أنصحك بمشاهدة محاضرته العامة الوجوه المتعددة للكون .

هذا الموجز هو محاولتي في التعليم الذاتي. ما زلت أكتبها لنفسي في دفتر ملاحظات. لكنني قررت الجمع بين العمل والمتعة. آمل أن يكون مثيرا للاهتمام لشخص ما أيضا.

قم بإجراء حجز على الفور حاولت تدوين الملاحظات بالقرب من النص الأصلي. ومع ذلك ، في بعض الأماكن ، سمحت لنفسي بتكملة أو تعميم بيانات المحاضر بناءً على تجربتي الخاصة كفيزيائي متخصص. وقد تم ذلك فقط لتسهيل فهم المواد واستيعابها واستيعابها.

في هذه المقالة ، يتم تقديم ملخص للمحاضرة رقم 1 لفت انتباهك. ربما ستظهر تكملة لاحقًا.

مراجعة تاريخية

علم الكونيات هو موضوع قديم جدا. يعود تاريخ علم الكونيات إلى آلاف السنين. على وجه الخصوص ، عرف الإغريق القدماء عن علم الكونيات لفترة طويلة جدًا.

تغطي هذه المحاضرات الفترة الزمنية التي لا تزيد عن النصف الثاني من القرن العشرين ، عندما اكتشف إدوين هابل قانون توسع الكون.

إذا تحدثنا عن علم الكونيات كعلم ، فهذا مجال جديد إلى حد ما من المعرفة. يعود تاريخ علم الكونيات الحديث إلى اكتشاف إشعاع بقايا الميكروويف وصياغة نظرية الانفجار العظيم . وقد حدث هذا فقط في الستينيات.

حتى هذه اللحظة ، لم يكن علم الكونيات فرعًا من الفيزياء ، بل كان ينتمي إلى العلوم الطبيعية. هذا هو ، في علم الكونيات ، ساد النهج الظواهري: الملاحظة والقياس والتصنيف والفهرسة ، إلخ.

في ذلك الوقت ، كانت دقة القياسات منخفضة. وبالتالي كان من المستحيل صياغة عبارات دقيقة. كانت هناك معادلات ، لكنها كانت غير صحيحة وغير دقيقة. شارك الفيزيائيون دائمًا في عملية الدراسة ، نظرًا لأن النجوم والمجرات والأجرام السماوية الأخرى تمتلك خصائص فيزيائية مثل الزخم الزاوي ، على سبيل المثال. كما شارك الكيميائيون الفيزيائيون ، لأن الأجرام السماوية لها تركيبة كيميائية.

ومع ذلك ، فإن الموقف من الكون نفسه كجسم مادي ، والكون كنظام يجب دراسته رياضيًا باستخدام مجموعة من المبادئ الفيزيائية والمعادلات الصحيحة الدقيقة المطابقة - هذا نهج حديث نسبيًا.

خصائص الكون

في هذه المحاضرات ، يعتبر الكون نظامًا ماديًا. وسندرسها باستخدام المعادلات. يمكننا أن نبدأ استكشافنا للكون ببعض الملاحظات العامة.

متناحي

لذا ، فإن الملاحظة الأولى ، التي ، بشكل عام ، قد لا تكون دقيقة تمامًا ، تمامًا مثل جميع الفيزياء ليست دقيقة تمامًا ، هي أن الكون متناحي .

يعني الخواص أن الكون يبدو كما هو في أي اتجاه. بالطبع ، هذا صحيح فقط لمسافات كبيرة بما فيه الكفاية. إذا نظرتم إلى مسافة قريبة جدًا ، فقد لا تتم ملاحظة التماثل بسبب عدم التجانس المحلي ، على سبيل المثال ، بسبب شكل مجرتنا.

التوحيد

إذا كان الكون موحد الخواص ، فيمكن القول بشكل مؤكد أن الكون يجب أن يكون متجانسًا أيضًا. التجانس لا يعني التوحيد في كل اتجاه ، ولكن في كل مكان. هذا ، على نطاق واسع ، يبدو الكون كما هو بغض النظر عن مكان وجود المراقب - في مجرتنا أو في مكان آخر ، بعيدًا جدًا عنا.

المجرات

المجرات على مقياس الكون هي نقاط تركيز كتلة فعالة. يمكننا معاملتهم كنقاط مادية. العدد التقريبي للمجرات في الجزء المرئي من الكون هو مائة مليار $$$10 ^ {11} = 100 \، 000 \، 000 \، $ 00$ . في المقابل ، تحتوي كل مجرة ​​أيضًا تقريبًا $$$10 ^ {11}$ مائة مليار نجم. يجب أن نتذكر أن هذا هو عدد المجرات فقط داخل المجال الذي يمكننا رؤيته. فقط بقدر ما يستطيع الفلكيون رؤيته بالتلسكوبات. أي أن أبعد ما يمكننا رؤيته هو على مسافة من حيث تمكن الضوء من الوصول إلينا طوال وجود الكون بأكمله: حوالي 13 مليار سنة.

حقيقة مثيرة للاهتمام. العدد الإجمالي للنجوم في الجزء المرئي من الكون $$$10 ^ {11} \ cdot 10 ^ {11} = 10 ^ {22}$ ، وإذا كان لكل نجم متوسطه 10 كواكب ، فعندئذٍ يتبين $$$10 ^ {23}$ - عدد كواكب Avogadro في الكون. الخلد الكواكب من الجوهر! (المحاضر يضحك)

حجة ضد تجانس الكون. نقض

تأمل قطعة من الكون حيث نحن. نحن نعلم بالتأكيد ، لأننا نرى أن الكون هو موحد الخواص . نفترض أن الكون متجانس أيضًا. لكن ماذا سيحدث لو لم يكن الكون متجانسًا؟

إذا كان الكون متناحيًا ، فإن الطريقة الوحيدة لكي لا يكون متجانسًا هي أن يكون له هيكل على شكل نوع من الأصداف.


فرضية كون غير متجانس. على اليسار كون متجانس متناحي ؛ على اليمين كون متناحي ليس متجانسًا. يشير الصليب في المركز إلينا.

إذا كان الأمر كذلك ، فلن يكون الكون في أي نقطة أخرى متناحية. أي ، إذا كنا لا نريد أن نصدق أننا بطريقة ما كنا في مركز الكون بالضبط ، وحتى يكون للكون بأكمله تناظر كروي من حولنا ، فعندئذ علينا أن نعترف بأن الكون ليس متساوي الخواص فحسب ، بل متجانس أيضًا.

مبدأ الكونية

لذا ، إذا كنا لا نعتقد أننا موجودون بالضبط في وسط الكون ، فيجب أن يكون الكون متجانسًا. الكون المتجانس يعني أن الكون مملوء بشكل موحد بالجسيمات (المجرات) في جميع أنحاء الحجم. وهذا ما يسمى بالمبدأ الكوني . المبدأ الكوني صحيح ، لأن ملاحظاتنا تشير إلى ذلك ، بالطبع ، إلى حد ما من التقريب.

يدعي بعض علماء الفلك أنهم لاحظوا عدم تجانس واسع النطاق في الكون. يشك المحاضر في مصداقية هذه المصادر والبيانات.

بطبيعة الحال ، فإن فكرة تجانس الكون ليست دقيقة تمامًا. حتى حقيقة وجود المجرات تشير بالفعل إلى وجود عدم تجانس. بالمناسبة ، ليس هناك مجرات فحسب ، بل هناك أيضًا مجموعات من المجرات. ومع ذلك ، على نطاق واسع إلى حد ما ، تقريبًا من حوالي مليار سنة ضوئية ، يبدو الكون متجانسًا.

في البداية ، كان المبدأ الكوني مجرد افتراض. ولكن مع تراكم بيانات المراقبة ، تم تأكيدها بشكل أكثر موثوقية ، وفي النهاية ، تم اكتشاف إشعاع الميكروويف المتبقي ، مما يشير إلى أن التوزيع الأولي للمادة في الكون كان متجانسًا للغاية.

بيان المشكلة الجسدية

هناك غاز موحد من جزيئات المجرة. وتتفاعل كل مجرة ​​مع المجرات الأخرى. المجرات ككل محايدة كهربائيًا. لكنهم ليسوا محايدين الجاذبية. تتفاعل من خلال الجاذبية النيوتونية. وهذه هي القوة المهمة الوحيدة على نطاق واسع. تعمل الجاذبية على المجرات وتحاول جمعها معًا.

لذا ، إذا نظرت إلى أي نقطة في الكون وتساءلت عن المكان الذي يجب أن تتحرك فيه ، يمكنك تخمين أنه محاط بنفس القدر من جميع الجوانب. باتباع هذا المنطق ، يمكن الافتراض أنه لا يجب أن تتحرك أي مجرة ​​على الإطلاق ، ويجب أن يكون الكون ثابتًا ، لأن القوى التي تعمل على أي نقطة في الكون هي صفر. هذا خطأ مطلق!

والآن نحصل على معادلات الحركة النيوتونية للكون. يمكنك أن تسمع أن الكون المتوسع يتفق جيدًا مع نظرية النسبية العامة لأينشتاين ، وأنه قبل النظرية النسبية العامة ، كان قانون الكون المتوسع غير مفهوم. هذا ببساطة غير صحيح. ربما كان هذا تاريخيا. لكن هذه ليست سوى حقيقة تاريخية حول التواريخ ، وليس حول المنطق. يمكن لنيوتن الحصول على معادلات الكون المتمدد. والآن سنفعل ذلك كما كان ينبغي أن يفعل نيوتن.

نظام الإحداثيات

في أي مشكلة مادية ، أول شيء يجب فعله هو إدخال نظام إحداثيات. بدلاً من اختيار خطوة الشبكة كمسافة: 1 متر ، مليون كيلومتر ، ألف سنة ضوئية ، سنختار شبكة بحيث ترتبط عُقدها بشكل صارم بالمجرات. بما أن الكون متجانس ، يمكننا القيام بذلك. ثم ستبقى المجرات دائمًا عند نفس الإحداثيات ، بغض النظر عما يحدث للكون. أي أن المجرات تبدو "مجمدة" في شبكة الإحداثيات.

ليس من الواضح على الإطلاق أنه يمكن القيام بذلك. إذا تحركت المجرات تمامًا عن طريق الصدفة وفي اتجاهات مختلفة تمامًا ، فلن نتمكن من القيام بذلك. لكننا نرى أن المجرات تتحرك بالصدفة. نرى أن المجرات تتحرك بشكل متناسق ، تمامًا كما لو كانت مدمجة في شبكة إحداثيات معينة. وما نراه يسمح لنا بالقيام بذلك ، لأن سرعات المجرات بالنسبة لبعضها البعض ثابتة وليست عرضية.

نقدم شبكة $$$(x، y، z)$ . لا يتم قياس هذه الإحداثيات بوحدات الطول. إذا اعتبرنا مجرتين مفصولتين بفاصل $$$\ Delta x$ ثم المسافة $$$D$ بينهما (بالأمتار)

$$

$$D = a \، \ Delta x$$

أين $$$a$ هي معلمة مقياس ، قد تكون ثابتة ، ولكن بشكل عام ، قد لا تكون. قد تعتمد معلمة المقياس على الوقت. $$$a = a (t)$ .

وهكذا ، من خلال نظرية فيثاغورس ، تتم كتابة المسافة بين مجرتين بشكل عام

$$

$$D = a (t) \ sqrt {\ Delta x ^ 2 + \ Delta y ^ 2 + \ Delta z ^ 2}$$

وبطبيعة الحال ، المعلمة $$$a$ ليست ثابتة. إذا كانت ثابتة ، فستكون المجرات ثابتة ، ولن تتحرك في أي مكان. وهذا ليس ما نلاحظه. نرى أنها تطير بعيدا.

قانون هابل

نكتب السرعة النسبية بين مجرتين. نحن نفرق بين الصيغة السابقة في الوقت المناسب. نحن نأخذ ذلك في الاعتبار $$$\ Delta x$ - هذا فاصل زمني ثابت لا يمكن تغييره وفقًا لشروط إنشاء نظام إحداثيات. ثم

$$

$$\ mathcal {V} = \ dot {a} \، \ Delta x$$

حيث نستخدم الترميز $$$\ dot {a} = da / dt$ .

نكتب الآن نسبة السرعة النسبية لمجرمتين إلى المسافة بينهما

$$

$$\ frac {\ mathcal {V}} {D} = \ frac {\ dot {a} (t)} {a (t)}$$

لاحظ ذلك $$$\ Delta x$ يتم تخفيض ، وهذه النسبة لا تعتمد على الإحداثيات على الإطلاق. أي أن هذه الصيغة صالحة لأي مجرتين ، بغض النظر عن مدى قربها أو قربها.

تسمى هذه العلاقة بمعامل ثابت هابل.

$$

$$H (t) = \ frac {\ dot {a} (t)} {a (t)}$$

ولا يعتمد على الإحداثيات. ثم يمكنك كتابة نفس الشيء في شكل قياسي

$$

$$\ mathcal {V} = H \، D$$

تتناسب السرعة النسبية لمجرمين مع المسافة بينهما.

عليك أن تفهم أننا ما كنا سنكتبه إذا لم يكتشف هابل قانونه. قانون هابل ، من ناحية أخرى ، ليس مفاجئًا للغاية. هناك قول مأثور: "ليس من المستغرب أن يركب أسرع حصان قبل الجميع". كلما تحركت أسرع ، كلما كنت. وهذه حقيقة اكتشفها هابل.

كتلة المادة في الكون

ضع في اعتبارك بعض الحجم $$$\ Delta x \، \ Delta y \، \ Delta z$ . نسأل سؤالا: ما هي الكتلة المركزة في هذا الحجم؟ دع $$$\ nu$ هي كتلة مادة في حجم أولي $$$dx \، dy \، dz$ (بالكيلوغرام). ثم الكتلة في الحجم $$$\ Delta x \، \ Delta y \، \ Delta z$ يساوي

$$

$$M = \ nu \، \ Delta x \، \ Delta y \، \ Delta z$$

ما هو الحجم المتري لهذه المنطقة؟ منذ ذلك الحين $$$D = a \، \ Delta x$ يمكننا الكتابة

$$

$$V = a ^ 3 \، \ Delta x \، \ Delta y \، \ Delta z$$

ما هي كثافة المادة في هذه المنطقة؟ بحكم التعريف ، الكثافة $$$\ rho = M / V$ ، أي مع مراعاة الصيغتين السابقتين ، نحصل على

$$

$$\ rho = \ frac {\ nu} {a ^ 3}$$

هذه هي الكثافة المادية القياسية للمادة.

على الرغم من أن إجمالي كمية الكتلة في الحجم $$$\ Delta x \، \ Delta y \، \ Delta z$ لا تتغير ، بما أن المجرات "مجمدة" في شبكة الإحداثيات ، فإن الكثافة المطلقة للمادة في نفس الحجم يمكن أن تتغير ، لأن المعلمة $$$a (t)$ يعتمد على الوقت.

نظرية نيوتن

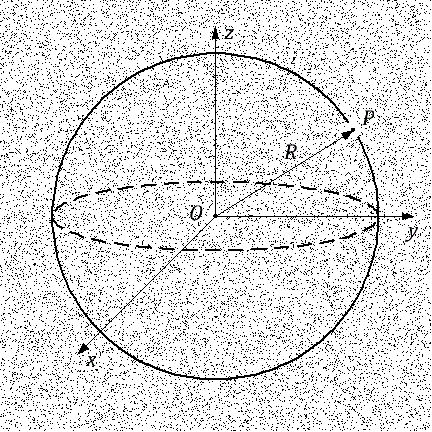رسم توضيحي لنظرية نيوتن

لنأخذ مجرتين. يمكننا دائمًا وضع أحدهم في الأصل. دع المجرة $$$O$ هو في الأصل ، والمجرة $$$P$ على مسافة منها.

تنص نظرية نيوتن على أن قوة الجاذبية تعمل على مجرة $$$P$ يعتمد فقط على كمية الكتلة داخل الكرة المتمركزة في الأصل $$$O$ ، ويمر عبر المجرة $$$P$ . البيان الثاني لنظرية نيوتن هو أن الكتلة بأكملها داخل هذا المجال يمكن اعتبارها مركزة في المركز عند الأصل عند النقطة $$$O$ شريطة أن يتم توزيع الكتلة داخل الكرة ، إن لم يكن بشكل موحد ، على الأقل متناحي .

وبعبارة أخرى ، تأثير الكتلة بأكملها داخل الكرة على المجرة $$$P$ تعادل كما لو كانت هذه الكتلة مركزة عند نقطة واحدة $$$O$ وهو مركز الكرة.

معادلات نيوتن للحركة

أوجد المسافة بين المجرات $$$P$ و $$$O$ . المجرة $$$P$ له إحداثيات $$$(x، y، z)$ ، أي المسافة من المركز إلى المجرة $$$P$ يساوي

$$

$$D = a (t) \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

يمكننا تقديم الترميز

$$

$$R = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

$$$R$ لا تقاس بالأمتار ، ولكن في نفس الوحدات $$$x$ ، $$$y$ و $$$z$ ولا يعتمد على الوقت. ثم

$$

$$D = a (t) \، R$$

نسجل الآن سرعة المجرة وتسارعها $$$P$

$$

$$\ mathcal {V} = \ dot {a} (t) \، R$$

$$

$$\ mathcal {A} = \ ddot {a} (t) \، R$$

الآن يجب أن نساوي التسارع $$$\ mathcal {A}$ إلى التسارع المرتبط بكتلة الجاذبية بأكملها داخل دائرة نصف قطرها $$$R$ . تشير إلى كتلة المجرة $$$P$ ل $$$م$ ، وكتلة كل المادة داخل الكرة وراءها $$$M$ . ثم قوة الجاذبية تعمل على المجرة $$$P$ يساوي

$$

$$F = -G \ frac {m \، M} {D ^ 2}$$

أين $$$G = 6.67408 \ times10 ^ {- 11} \ mathrm {N \ cdot m ^ 2 \ cdot kg ^ {- 2}}$ - ثابت الجاذبية. تعني علامة الطرح في الصيغة أنها قوة جذابة.

الآن يمكنك تسجيل تسارع المجرة $$$P$

$$

$$\ mathcal {A} = -G \ frac {M} {D ^ 2}$$

نحن نساوي تعبيرين عن $$$\ mathcal {A}$ واحصل

$$

$$\ ddot {a} (t) \، R = -G \ frac {M} {D ^ 2}$$

نحن نأخذ ذلك في الاعتبار $$$D = a \، R$ ثم

$$

$$\ ddot {a} \، R = - \ frac {M \، G} {a ^ 2 \، R ^ 2}$$

اقسم كلا الجانبين على $$$a \، R$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {M \، G} {a ^ 3 \، R ^ 3}$$

أوجد حجم الكرة

$$

$$V = \ frac {4} {3} \ pi \، D ^ 3 = \ frac {4} {3} \ pi \، a ^ 3 \، R ^ 3$$

نضرب بسط ومقام الجانب الأيمن في $$$4 \ pi / 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4} {3} \ pi \، G \، \ rho$$

هذه المعادلة مستقلة عن $$$R$ وهذا صحيح لأي مجرة ​​في الكون. هذه المعادلة هي المعادلة الأساسية المركزية لعلم الكونيات .

إحدى نتائج هذه المعادلة أنه من المستحيل أن يكون الكون ثابتًا إذا لم يكن فارغًا. يستتبع من هذه المعادلة أنه لا يمكن أن يكون الكون ساكنًا إلا إذا كان فارغًا.

يمكننا إعادة كتابة هذه المعادلة ، بالنظر إلى ذلك $$$\ rho = \ nu / a ^ 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4 \ pi} {3} \ frac {G \، \ nu} {a ^ 3}$$

تم الحصول على هذه المعادلة لأول مرة في سياق النظرية النسبية العامة بواسطة ألكسندر فريدمان. هذه المعادلة لا تخبرنا ما إذا كان الكون يتمدد أو يتقلص. تقول فقط أن المشتق الثاني من عامل المقياس هو سلبي. أي أنه إذا تمدد الكون ، فإنه يتباطأ ، وإذا انكمش الكون ، فإنه يتسارع.

في الواقع ، الكون يتوسع ولا يتباطأ. لقد فعلنا للتو ما يمكن أن يفعله نيوتن والذي اعتبره جميع علماء الكونيات صحيحًا حتى عام 1998 تقريبًا. تم قبول هذا النموذج بشكل عام وكان يسمى النموذج القياسي للكون حتى تم اكتشاف التوسع المتسارع للكون علنا. حتى الآن ، الطرف الأيمن من المعادلة له مصطلح واحد فقط. في الواقع ، يجب أن يكون هناك العديد من المصطلحات التي ترتبط بالنظرية النسبية العامة.

سرعة المغادرة

اكتب الآن الطاقة الكاملة للمجرة $$$P$ كمجموع الحركية والإمكانيات

$$

$$E = \ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \، M} {D}$$

يمكن أن تكون الطاقة إيجابية أو سلبية اعتمادًا على النسبة بين هذين المصطلحين. من المهم أيضًا أن نتذكر أن الطاقة الإجمالية للجسيم $$$P$ تم الحفظ. إذا كانت الطاقة الإجمالية موجبة ، فلن يتمكن الجسيم من العودة. يعود الجسيم إلى الوراء فقط عندما تكون الطاقة الكلية سالبة. حالة الحدود هي إجمالي الطاقة صفر. حل المعادلة $$$E = 0$ ل $$$\ mathcal {V}$ للعثور على سرعة المغادرة.

$$

$$\ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \، M} {D} = 0$$

$$

$$\ mathcal {V} _ {0} = \ frac {2MG} {D}$$

تمامًا مثل المجرة $$$P$ يمكن أن يكون للكون بأكمله سرعة أعلى من سرعة المغادرة وأقل من سرعة المغادرة أو مساوية لسرعة المغادرة. إذا كانت سرعة الكون أعلى من سرعة الانطلاق ، فعندئذٍ يتمدد ولا يبدأ في الانكماش أبدًا ؛ إذا كانت سرعة الكون أقل من سرعة الانطلاق ، فعندئذٍ سيبدأ في الانكماش عاجلاً أم آجلاً.

أعد كتابة معادلة الطاقة الكلية

$$

$$\ frac {1} {2} m \، \ dot {a} ^ 2 R ^ 2 - \ frac {m \، MG} {aR} = E$$

معادلة فريدمان

ضع في اعتبارك الحالة عندما تتزامن سرعة الكون مع سرعة الانطلاق.

$$

$$\ frac {1} {2} m \، \ dot {a} ^ 2 R ^ 2 - \ frac {m \، MG} {aR} = 0$$

بسّط التعبير: القسمة على $$$م$ ، اضرب في 2 ، قسمة على $$$a ^ 2 R ^ 2$

$$

$$\ frac {\ dot {a} ^ 2} {a ^ 2} - \ frac {2MG} {a ^ 3R ^ 3} = 0$$

في المصطلح الثاني ، نضرب البسط والمقام في $$$4 \ pi / 3$ . ثم في المقام نحصل على الحجم المتري للكرة $$$V$ . بالنظر إلى ذلك $$$M / V = ​​\ rho$ نحصل

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} G \ rho$$

وهذا ما يسمى معادلة فريدمان . وهي تعادل المعادلة النيوتونية التي تم الحصول عليها أعلاه. بما أننا افترضنا أن الطاقة الإجمالية هي صفر ، فإن مثل هذا الكون يتوسع ، ويتباطأ بشكل تقريبي إلى الصفر ، لكنه لا يعبر الصفر أبدًا ولا يبدأ في الانكماش.

أذكر الآن ذلك $$$\ rho = \ nu / a ^ 3$ . أعد كتابة معادلة فريدمان

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ frac {\ nu G} {a ^ 3}$$

معلمة $$$\ nu$ مرن جدا.يعتمد ذلك بشكل كامل على اختيارنا للشبكة. وبصفة عامة ، يمكننا حتى اختيار ذلك$$$\frac{8\pi}{3}\nu G = 1$ . ثم

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{1}{a^3}$$

دائمًا ما يكون الجانب الأيمن من هذه المعادلة موجبًا ، وبالتالي معدل التوسع
$$˙ و لم يصبح صفرا. أذكر الآن ذلك$\dot{a}$$$˙ a /a=Hهيمعلمةثابتهابل. ويترتب على المعادلة أيضًا أن معلمة هابل لا تتغير أبدًا. ومع ذلك ، فإنه لا يزال يتباطأ. تصبح معلمة هابل أقل وأقل بمرور الوقت. هذه المعادلة مهمة للغاية لجميع علم الكونيات. طريقة بسيطة لحلها هي البحث عن حل من نوع معين ، أي أننا سنبحث عن حل في النموذج$\dot{a}/a = H$

$$

$$a(t) = c\,t^p$$

أين $$$c$ و $$ع بعض الثوابت.$p$

$$

$$\dot{a} = c\,p\,t^{p-1}$$

$$

$$\frac{\dot{a}^2}{a^2} = \frac{p^2}{t^2}$$

$$

$$\frac{p^2}{t^2} = \frac{1}{c^3\,t^{3p}}$$

$$

$$3p = 2\\ p^2 = \frac{1}{c^3}$$

$$

$$p = \frac{2}{3}\\ c = \left(\frac{3}{2}\right)^{\frac{2}{3}}$$

لقد حصلنا على حل لمعادلة فريدمان.


رسم بياني لحل معادلة فريدمان

الكون الحقيقي يتبع هذا القرار حتى وقت معين فقط ، ثم يبدأ في التسارع. يمكن لنيوتن القيام بذلك. اقترب جدا. طرح جميع الأسئلة الصحيحة. المحاضر واثق من أن نيوتن ، على الأرجح ، فعل ذلك وحصل على هذا القرار. ومع ذلك ، كانت هذه المعلومات عن الكون مخالفة لوجهات نظره الدينية ، وبالتالي لم ينشر اكتشافاته.