هل يمكنني الفوز بالمقامرة؟ محاكاة بايثون

مرحبًا Geektimes.

في عملية التباطؤ الخامل ، نشأت الفكرة لدراسة القمار المختلفة ، في نفس الوقت لفهم كيفية عملها بشكل أفضل. كانت النتائج ، على الرغم من أنها واضحة بشكل عام ، مثيرة للاهتمام بما يكفي لمشاركتها مع الجمهور.



لمن التفاصيل مثيرة للاهتمام ، أسأل تحت القط.

النرد: لعبة الكرابس

على الأرجح ، خيار بسيط ومفهوم - هناك مكعب به علامات من 1 إلى 6 ، واحتمال سقوط رقم معين هو 1/6. لكن اللعب بهذه الطريقة سيكون مملاً ، لذلك تحظى الألعاب ذات القواعد الأكثر تعقيدًا بشعبية. لعبة الحظ الشائعة هي لعبة الكرابس ، وتظهر الصورة أعلاه صورة لطاولة اللعبة. كما ترى ، هناك الكثير من كل شيء ، لكننا لن ندخل في الخفايا العميقة.

تتكون كل دورة في اللعبة من رمي نردين ، تتم إضافة النقاط المتراكمة. كما يقول المقال ، "قواعد اللعبة مباشرة: اللاعب يتدحرج نردتين ، وإذا كان مجموع النقاط عليهما 7 أو 11 ، يفوز ، إذا خسر 2 أو 3 أو 12. عندما تقع كمية مختلفة على الزهر ، يرميها مطلق النار إلى تركيبة رابحة أو خاسرة ".

دعونا نرى كم يمكنك الفوز بهذه الطريقة. ليس من الضروري الذهاب إلى كازينو لذلك ، سنستخدم Python لمحاكاة اللعبة. نكتب دالة لرمية واحدة:

import random def shoot(): return random.randint(1,6) + random.randint(1,6) 

سنكتب وظيفة محاكاة خطوة واحدة وفقًا للقواعد المذكورة أعلاه.

 def move(): while True: val = shoot() print "Dice roll:", val if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False 

لنقم بتعيين لاعبنا الافتراضي بمبلغ مبدئي قدره 100 دولار ، وبدء عملية اللعبة. دع لاعبنا يضع 100 رهان ، في كل مرة 1u.e.

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

نبدأ محاكاة 100 مباراة ونفاجأ بالنتيجة ، فاز اللاعب بهامش ملحوظ من الانتصارات من الهزائم: Win 63 ، Loss 37 ، Money 126. نزيد عدد الألعاب إلى 1000 ونجري مرة أخرى ، فاز اللاعب مرة أخرى: Win 680 ، Loss 320 ، Money 460 .

من الواضح أن هناك شيئًا خاطئًا هنا - لعبة يكون فيها اللاعب دائمًا باللون الأسود ، بالكاد تحظى بشعبية في الكازينو ، ستنكسر ببساطة. دعونا نحاول معرفة ذلك.

يبدو أنه من البديهي أنه عند رمي النرد ، فإن احتمال سقوط أي وجه محتمل على حد سواء. وهذا صحيح ، ولكن في حالة مكعب واحد . إذا كان هناك مكعبان ، يصبح كل شيء أكثر تعقيدًا. على سبيل المثال ، يمكن أن يسقط الرقم 7 كـ 3 + 4 ، 2 + 5 ، 1 + 6 ، لكن الرقم 12 يمكن أن يسقط فقط كمزيج من 6 + 6.

في مفكرة Jupyter ، نقوم بإنشاء جدول زمني لفقدان المبالغ من 1 إلى 12 مقابل 100 رمية:

 from matplotlib import pyplot as plt %matplotlib inline y = [ shoot() for v in range(100) ] plt.hist(y) 

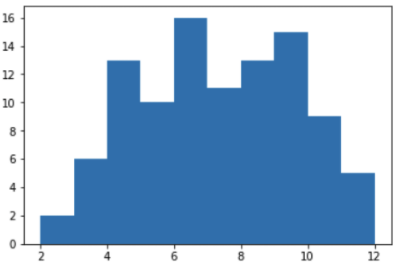
تم تأكيد الافتراض ، والمبلغ من المركز يسقط في كثير من الأحيان. وبالتالي ، فإن الرقمين 7 و 11 يسقطان بالفعل أكثر من 2.3 أو 12. واحتمال الحصول على تركيبة فائزة "7 أو 11" أعلى حقًا.

كيف يكون هذا؟ للأسف ، الجواب بسيط - مؤلف المقالة المذكورة أعلاه ببساطة لم يفهم تمامًا قواعد اللعبة. النص " قواعد اللعبة واضحة: اللاعب يتدحرج نردتين ، وإذا كان مجموع النقاط عليها 7 أو 11 ، يفوز ، إذا كانت 2 أو 3 أو 12 - يخسر " بعيدًا جدًا عن الحقيقة ، والقواعد في الكرابس ليست مباشرة كما تبدو .

تبين أن القواعد الحقيقية للمراهنة على خط المرور أكثر تعقيدًا بقليل (هناك أنواع أخرى من الرهانات يمكن للأشخاص الذين يرغبون في اكتشافها بأنفسهم).

الخطوة 1 : يتم عمل لفة. إذا سقط 7 أو 11 ، يفوز اللاعب ؛ إذا 2 أو 3 أو 12 ، يخسر اللاعب. إذا وقع رقم آخر ، يتم تذكره تحت نقطة الاسم.

الخطوة 2 : يتم عمل لفة. إذا سقطت 7 ، فسيخسر اللاعب. إذا سقطت النقطة ، ففاز اللاعب. إذا انخفضت الأرقام الأخرى ، يتم تكرار الحركة (في هذا الوقت ، يمكن للاعبين أيضًا المراهنة على الأرقام الأخرى).

في الواقع ، كل شيء أكثر تعقيدًا قليلاً مما هو موضح في النسخة الأصلية. نضيف وظيفة محاكاة مع مراعاة القواعد الأكثر دقة.

 def move(): point = 0 while True: val = shoot() if point == 0: # First move if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False point = val else: # 2..N move if val == 7: return False if val == point: return True 

النتيجة الآن أكثر تشابهًا مع الحقيقة: بالنسبة لـ 100 مباراة ، فاز اللاعب 43 مرة ، وخسر 57 مرة ، وكان الرصيد في نهاية اللعبة 86.u. من أصل 100. ومن المثير للاهتمام أيضًا أن عدد الانتصارات كان كبيرًا جدًا ، وأقل بقليل من 50 ٪. هذه إستراتيجية مختصة من وجهة نظر الكازينو - تسمح لك بالحفاظ على اهتمام المشارك في اللعبة (سيكون من غير المثير للاهتمام أن تفقد كل الوقت) ، ولكن في نفس الوقت ، يبقى رصيد أرباح الكازينو إيجابيًا ، وبالتالي فإن رصيد أموال اللاعب سلبي.

دعونا نرى بمزيد من التفصيل ما تم الحصول عليه لمحاكاة 100 لعبة.
- فرصة الفوز في الخطوة الأولى تراجعت في حوالي 20 حالة.
- تراجعت فرصة الخسارة فوراً في الخطوة الأولى في 15 حالة.
- في الحالات الـ 65 المتبقية ، تستمر اللعبة ، وكل شيء صعب: يأتي الاختيار من رقمين ، 7 ونقطة ، ولكن كما ترى من الرسم البياني أعلاه ، فإن احتمال سقوط الرقم 7 "الخاسر" هو الحد الأقصى ، والذي كان يجب إثباته بشكل عام.

من المثير للاهتمام ملاحظة أن فرصة الفوز بنسبة 45٪ مرتفعة إلى حد ما. فهل من الممكن الفوز؟ على المدى القصير ، على سبيل المثال ، في محاكاة أخرى ، كان اللاعب "محظوظًا" ، وفي 100 مباراة قام بزيادة رأسماله الافتراضي من 100 إلى 112ye.



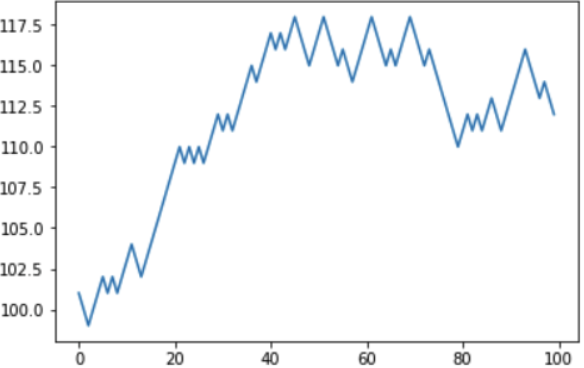
ولكن بالفعل أظهرت المحاكاة التالية توازنًا سلبيًا: قام اللاعب بتخفيض حالته من 100 إلى 88ye ، بعد أن خسر ، بالمناسبة ، نفس "12 فاز" في المرة السابقة.

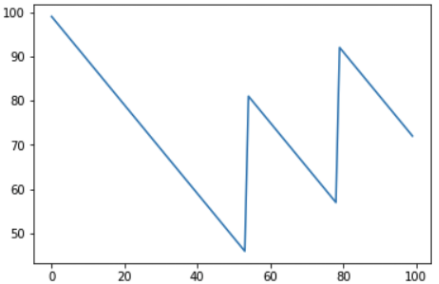
إذا قمت بزيادة عدد التكرارات إلى 1000 ، يمكنك أن ترى كيف قد يبدو الرصيد النقدي للاعب على المدى الطويل:



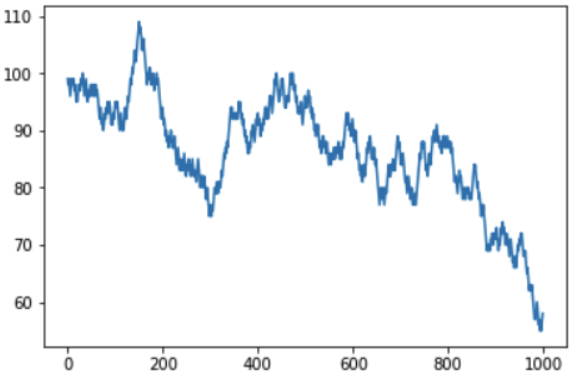
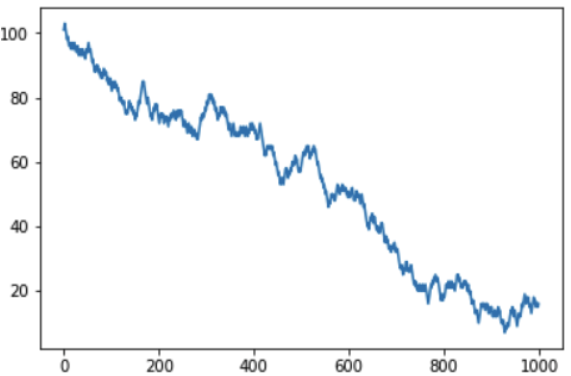
من الواضح أنه مع احتمال فوز كل مباراة بأقل من 50٪ ، فإن المبلغ الناتج في حساب اللاعب سينخفض ​​تدريجيًا ، وسيزداد مقدار ربح الكازينو تدريجيًا. بالمناسبة ، تظهر الانفجارات والسقوط على الرسم البياني ، وقد ينشأ سؤال معقول - هل يمكن توقعها؟ للأسف لا لأن القوائم النرد هي أحداث مستقلة عن بعضها البعض ، ولا تؤثر النتائج السابقة على ما يلي بأي شكل من الأشكال. يمكنك تكرار الفكرة الرئيسية مرة أخرى - يمكنك الفوز مرة واحدة أو حتى عدة مرات ، ولكن على المدى الطويل من المستحيل البقاء في زائد في الكازينو ، يتم وضع قواعد اللعبة بحيث لا يكون الرصيد لصالح اللاعب.

هناك أنواع أخرى من الرهانات في لعبة الكرابس ، ويمكن لأولئك الذين يرغبون في تحليلها بمفردهم.

الروليت الأمريكية

النوع التالي من المقامرة هو الروليت ، فكر في نسخته الأمريكية.



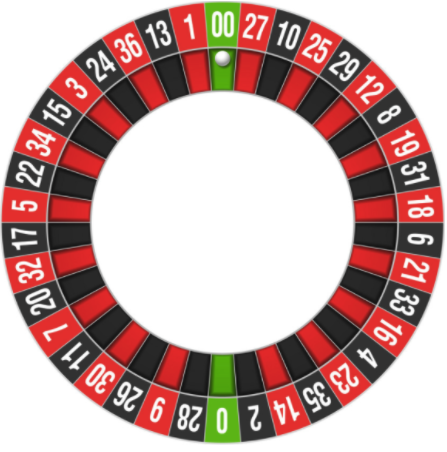
ينقسم ملعب الروليت إلى 38 خلية: 36 منطقة بأرقام + منطقتين "صفر" و "صفر مزدوج". من الواضح أن الكرة التي يتم رميها على عجلة الروليت ستتوقف في إحدى المناطق. يمكن للاعب أن يضع مجموعة متنوعة من الرهانات ، منها أكثر من 10 أنواع ، فكر في بعضها.

أسود أحمر (أو فردي)

يفوز اللاعب إذا تزامن الرهان الذي يسميه. من الواضح أن احتمالية أن يكون اللون الأسود أو الأحمر 50/50 ، إذا لم يكن لحقلي صفرين - إذا ضربهما ، يخسر الرهان. كما هو الحال في الكرابس ، هذا يجعل من احتمال الفوز أقل بقليل من 50٪ فقط - لكن هذا "قليلاً" يكفي ليكون في المنطقة الحمراء.

سنكتب وظيفة محاكاة الحركة باستخدام أرقام عشوائية من 1 إلى 38 ، وسيتم اعتبار آخر رقمين على أنه "صفر".

 def move_roulette1(): val = random.randint(1,38) if val == 37 or val == 38: return False return val % 2 != 0 

قم بتشغيل المحاكاة لـ 100 لعبة ، الرمز هو نفسه كما في محاكاة الكرابس ، نقوم فقط بتغيير استدعاء الوظيفة.

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette1() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

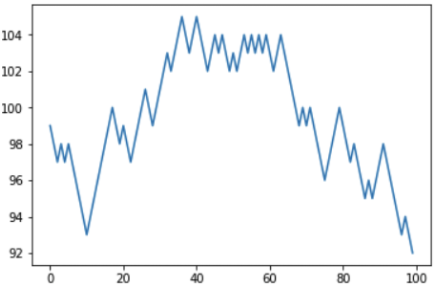
النتيجة: في 100 محاولة ، فاز اللاعب 46 مرة وخسر 54 مرة. يظهر الرسم البياني أن اللاعب لديه "صعود" و "انخفاض" ، ولكن الرصيد النهائي لا يزال سلبيًا.



كلما لعبنا أكثر ، كلما تعمقنا في الطرح ، والكازينو ، على التوالي ، في زائد:



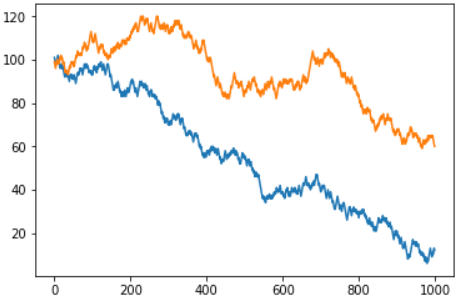
كان هناك سؤال من القارئ لماذا لم أفكر في لعبة الروليت الأوروبية مع حقل "صفر" واحد - كما قد تعتقد ، فإن فرصة الفوز هناك أعلى حقًا ، لكن المبدأ العام لا يتغير. في الواقع ، الفرق هو فقط في "سرعة الخسارة". هنا هو الجدول المشترك للنسختين الأمريكية والأوروبية من اللعبة:


يمكن لأولئك الذين يرغبون في اختبار النسخة الأوروبية من الروليت مع 37 فتحة استخدام الخيار الثاني للوظيفة:

 def move_roulette1(): val = random.randint(1,37) if val == 37: return False return val % 2 != 0 

راهن على رقم معين

يمكن للاعب أيضًا المراهنة على رقم معين ، الرهان على الفوز هو 35: 1. يبدو الأمر رائعًا ، ولكن من السهل تخمين أن احتمال سقوط رقم معين في الروليت هو 1:38 ، أي مرة أخرى ، أقل بقليل.

دعنا نضيف دالة الرهان إلى رقم محدد:

 def move_roulette2(num): val = random.randint(1,38) return val == num 

المحاكاة ، نفترض أن اللاعب يضع الرقم 10:

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette2(10) if step is True: money_total += 35*bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

ونتيجة لذلك ، فاز اللاعب مرتين وخسر 98 مرة ، والرصيد النهائي هو -28 وحدة.



راهن على رقمين

يمكنك المراهنة على رقمين - فرصة الفوز أعلى ، ولكن الرهان أقل وهو 17: 1.

لنكتب دالة:

 def move_roulette3(num1, num2): val = random.randint(1,38) return val == num1 or val == num2 

في 100 محاولة لمحاكاة ، فاز اللاعب 3 مرات وخسر 97 مرة ، كان الرصيد -46u.e.

هناك أنواع أخرى من الرهانات ، على سبيل المثال ، لأربعة أرقام بمعامل 1: 8 ، يمكن لأولئك الذين يرغبون في التجربة بمفردهم. كما قد تخمن ، تم تصميم جميع الاحتمالات بحيث يكون اللاعب باللون الأحمر. يبدو من المغري وضع 1ye على الرقم للفوز بما يصل إلى 35 درجة. لكن المبلغ الفائز يزيد بمقدار 35 مرة ، وتقل فرصة الفوز 38 مرة - سيظل الرصيد النهائي لصالح الكازينو.

6 لوتو من أصل 45

الشيء التالي المثير للاهتمام هو التحقق من اللوتو. مبدأ اللعبة بسيط للغاية - هناك 45 كرة في الطبل ، 6 منها تسقط بشكل عشوائي. سعر التذكرة وفقًا لموقع Gosloto هو 100 روبل ، وتعتمد الجائزة على عدد الكرات التخمينية. الترتيب التقريبي للمكاسب هو كما يلي: الكرتان المتخمين تعطيان الفوز بـ 100r ، 3 الكرات التخمينية تعطي 300r ، 4 الكرات - 3000r ، 5 الكرات - 300.000r و 6 الكرات - جائزة سوبر حوالي 10.000.000r.

أولاً ، اكتب برنامجًا لرمي الكرات ومقارنة النتيجة:

 def lottery(values): balls = range(1, 45+1) b1 = balls.pop(random.randint(0, len(balls)-1)) b2 = balls.pop(random.randint(0, len(balls)-1)) b3 = balls.pop(random.randint(0, len(balls)-1)) b4 = balls.pop(random.randint(0, len(balls)-1)) b5 = balls.pop(random.randint(0, len(balls)-1)) b6 = balls.pop(random.randint(0, len(balls)-1)) s = [b1,b2,b3,b4,b5,b6] res = list(set(s) & set(values)) return len(res) 

كرة عشوائية "تحصل" 6 مرات من مصفوفة الكرات ، ثم يتم تحديد عدد عناصر تقاطع مجموعتين. الآن سنقوم بإنشاء رسم بياني للمكاسب الإجمالية على عدد التذاكر المشتراة. من أجل البساطة ، نفترض أن اللاعب يراهن على نفس الأرقام.

 money = [] money_total = 0 ticket_price = 100 for p in xrange(N): val = lottery([3,7,12,18,33,28]) if val == 2: money_total += 100 if val == 3: money_total += 300 if val == 4: money_total += 3000 if val == 5: money_total += 300000 if val == 6: money_total += 10000000 money.append(money_total) x = range(0, N) price = map(lambda x: ticket_price*x, x) from matplotlib import pyplot as plt %matplotlib inline plt.plot(price, money) 

لفهم ترتيب الحجم: إذا قمت بشراء 100 تذكرة (سيكون المبلغ الإجمالي الذي تم إنفاقه 10.000r) ، فإن هذا يعطي 14 كرة "مزدوجة" خميرة وواحدة "ثلاثية". إجمالي الربح حوالي 2000r مع إنفاق 10000r.

جدول العوائد للمبلغ الذي تم إنفاقه يكاد يكون خطيًا:



اتضح أنه إذا اشتريت تذاكر بالمليون ، فسيكون الربح 250 ألفًا. لم تسقط "الجائزة الفائقة" في المحاكاة على الإطلاق ، رغم أنها ممكنة نظريًا بالتأكيد. بالمناسبة ، كما هو مكتوب في القواعد ، فإن مجموع الجوائز هو 50 ٪ من التذاكر المباعة ، لكن "الجائزة الفائقة" لا تسقط دائمًا ، كما هو الحال مع الكازينو ، بالطبع يفوز المنظمون دائمًا.

ماكينات القمار

كما أنها تعمل على مبدأ عشوائي (زائف) ، لأن "الزائفة" كانت الشفرة فيها مبرمجة منذ فترة طويلة وليس لديها ميكانيكا نظيفة. تعمل المبادئ العامة الموضحة أعلاه لأجهزة القمار أيضًا ، وعلى الأرجح لن تكون الرسومات مختلفة ، يمكن لأولئك الذين يرغبون في إضافة وظيفة المحاكاة بأنفسهم.

مقال جيد عن تصميم آلات الألعاب كان بالفعل على Geektimes.

الخلاصة

ربما لم تفتح هذه المقالة أمريكا للكثيرين ، ولكن على الرسوم البيانية ، من حيث المبدأ ، أكثر بصرية. اتضح أنه من المثير للاهتمام مقارنة نهج نفسي مختلف جوهريًا باللعبة. من المحتمل أن تكون الأرباح في اليانصيب كبيرة ، ولكنها نادرة جدًا. في الكازينوهات ، يكون الاتجاه عكس ذلك - يتم تكوين الرهانات بحيث يفوز الشخص في كثير من الأحيان. بشكل مشروط ، بعد إجراء 10 مباريات في كازينو ، سيفوز الشخص 4 مرات ويخسر 6 مرات. هذا يسمح للاعب بعدم فقدان الاهتمام باللعبة ، ولكن على أي حال ، يبقى الرصيد الإجمالي سلبيًا - سيفوز الشخص عدة مرات ، ولكنه يفقد أيضًا أكثر قليلاً .

ربما يكون هذا واضحًا بالفعل ، ولكن المقالة تدور فقط حول الألعاب القائمة على العشوائية ، وليس حول البوكر والبطاقات والشطرنج وما إلى ذلك. هل يمكن أن تكون هناك "استراتيجية فائزة" في هذه الألعاب العشوائية؟ من الواضح لا ، لأنه لا ذاكرة ، ولا كرة ، ولا تذاكر يانصيب لها ذاكرة ، ولا يعتمد سلوكها على التكرارات السابقة. بالمناسبة ، من المهم أن تتذكر هذه اللحظة - بشكل حدسي ، بعد أن خسر عدة مرات ، يمكن للشخص أن يقرر أنه سيفوز "بالتأكيد". للأسف ، لا توجد لعبة روليت أو تموت ، ولا يعرفون عدد المحاولات السابقة ، فكل لعبة تبدأ بشكل أساسي بأردواز نظيف.

الإجابة على السؤال في عنوان المقالة - هل من الممكن الفوز بالمقامرة؟ كما تظهر المحاكاة ، من الممكن من حيث المبدأ ، تعترف نظرية الاحتمالات. ولكن ليس لفترة طويلة - من الجدير البدء في اللعب في المرة الثانية والثالثة والثالثة ، حيث ينخفض ​​الرصيد. على المدى الطويل ، من المستحيل الفوز في الكازينو.

ملاحظة: بالنسبة لأولئك الذين يرغبون في التجربة ، يتم وضع شفرة المصدر في ملف واحد تحت المفسد. يمكن تشغيله في Python IDE عبر الإنترنت ، على سبيل المثال هنا . لاختبار النسخة الأوروبية من الروليت بدلاً من الأمريكية ، يكفي تغيير 38 إلى 37 في الكود.هذه المحاكاة أساسية تمامًا ، ولا تأخذ في الاعتبار عوامل إضافية مختلفة ، مثل مبلغ المال الذي يملكه اللاعب أو الحد الأقصى للرهانات في الكازينو ، أولئك الذين يرغبون في إضافة كل هذا بشكل مستقل. تحت المفسد ، يمكنك أيضًا مشاهدة نسخة فيديو من هذه المقالة.