 ما الرقم الذي يجب إدراجه في المثلث الأخير؟
ما الرقم الذي يجب إدراجه في المثلث الأخير؟يحل العلماء المشاكل ؛ هذا هو عملهم. ولكن ما هي المهام التي ستكون واعدة للبحث؟ للإجابة على هذا السؤال ، كتبت كتاب
Lost in Maths ، حيث درست المشاكل المتعلقة بأساسيات الفيزياء.
يمكن تنظيم التصنيف الأولي التقريبي لمشاكل البحث باستخدام
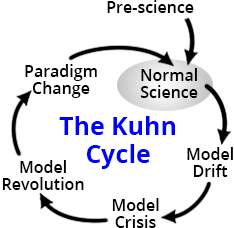
دورة تطوير النظريات العلمية لتوماس كون. تتكون دورة Kuhn من مرحلة "العلم العادي" ، تليها "أزمة" تؤدي إلى تحول نموذجي ، وبعد ذلك تبدأ مرحلة جديدة من "العلم العادي". هذا تبسيط مذهل للواقع ، ولكنه مناسب للتفكير اللاحق.
المهام المشتركة
خلال مرحلة العلوم العادية ، يمكن صياغة أسئلة البحث عادةً على أنها "كيف نقيس ذلك؟" (للمجربين) و "كيف نحسب هذا؟" (لمنظرى).
إن أساسيات الفيزياء مليئة بهذه "المشاكل العادية". يعاني المجربون من العديد من المشاكل ، لأن جميع المشكلات التي تم حلها بسهولة تم حلها بالفعل ، كما أن تعقيد قياس شيء جديد يتزايد باستمرار. تنبع مشكلات المنظرين من حقيقة أن التنبؤات في الفيزياء لا تسقط من الفرضيات بمفردها. غالبًا ما يُطلب منه المرور بمراحل عديدة من الجدل وإجراء العديد من الحسابات الطويلة للوصول إلى العواقب العددية للافتراضات النظرية.
من الأمثلة الجيدة على مشكلة شائعة في أساسيات الفيزياء المادة المظلمة الباردة. الفرضية بسيطة للغاية: في الفضاء هناك شيء بارد ومظلم يتصرف مثل السائل ويتفاعل بشكل ضعيف مع نفسه ومع المواد الأخرى. لكن هذا في حد ذاته ليس تنبؤًا مفيدًا بشكل خاص. ستكون المهمة البحثية الجيدة هي: "كيف تؤثر المادة المظلمة الباردة على تقلبات درجة حرارة مادة CMB؟" ثم يأتي السؤال التجريبي: "كيف نقيس هذا؟"
المهام الأخرى من هذا النوع في أساسيات الفيزياء هي: "ما هي مساهمة الجاذبية في العزم المغناطيسي للميون؟" و "ما هي خلفية تشتت الفوتون في مصادم هادرون الكبير؟"
تزيد الإجابات على هذه المهام المشتركة من فهمنا للنظريات الموجودة. يمكن إجراء هذه الحسابات داخل منصاتنا الحالية ، ولكن يمكن أن تكون معقدة للغاية.
يتم حل المهام المعطاة في الفقرات السابقة كأمثلة ، أو على الأقل نعرف كيفية حلها ، على الرغم من أنه من الممكن دائمًا طلب دقة محسنة. ولكن في هذه الفئة هناك أيضًا مشاكل لم يتم حلها.
على سبيل المثال ، يجب أن تتنبأ النظرية الكمومية للتفاعل النووي القوي بكتل الجسيمات التي تتكون من عدة كواركات - النيوترونات والبروتونات والجسيمات المركبة الأخرى المماثلة (ولكن غير المستقرة). لكن هذه الحسابات معقدة للغاية. اليوم يتم تنفيذها باستخدام برامج كمبيوتر معقدة - حسابات شعرية - وما زالت توقعاتهم ليست جيدة. السؤال ذو الصلة هو كيف تتصرف المادة النووية في نوى النجوم النيوترونية.
هذه مجرد أمثلة عشوائية مختارة للعديد من الأسئلة المفتوحة للفيزياء ، والتي هي "مشاكل طبيعية" ، والتي ، كما يعتقد ، يمكن العثور عليها في إطار النظريات المعروفة لدينا بالفعل - ولكن أعتقد أنها توضح هذا الموضوع جيدًا.
إذا تجاوزنا الأساسيات ، فإن لدينا مهام عادية مثل التنبؤ بالدورات الشمسية والطقس المشمس - فهي معقدة بسبب عدم الخطية الشديدة والاضطراب الجزئي للنظام ، لكننا لا نتوقع منهم أن يتعارضوا مع النظريات الحالية. لا تزال هناك موصلية فائقة درجة حرارة عالية ، وهي دراسة مدروسة جيدًا ، لكنها ظاهرة غير مفهومة نظريًا بشكل غير كاف ، حيث تفتقر هذه المواد إلى الجسيمات شبه. وهكذا دواليك.
هذه هي المهام التي ندرسها عندما يسير كل شيء وفقًا للخطة. ولكن لا تزال هناك مهام يمكنها ، من حيث المبدأ ، تغيير النماذج ، وهي المهام التي تشير إلى وجود "أزمة" في مصطلحات Kuhn.
مهام الأزمات
مهام الأزمات الواضحة هي ملاحظات لا يمكن تفسيرها على أساس نظريات معروفة.
أنا لا أعتبر غالبية الملاحظات المتعلقة بالمادة المظلمة والطاقة المظلمة كملاحظات أزمات. يمكن تفسير معظم هذه البيانات بشكل جيد عن طريق إضافة مكونين جديدين إلى ميزانية الطاقة في الكون. بالطبع ، ستشتكي من أن هذا لن يعطينا وصفًا مجهريًا ، ولكن ليس لدينا بيانات عن الهياكل المجهرية ، لذلك لا يزال يتعذر علينا صياغة المشكلة.
لكن بعض ملاحظات المادة المظلمة تنتمي إلى "الأزمة". الارتباطات التي لا يمكن تفسيرها ، والأنماط في المجرات ، والتي يصعب تفسيرها بمساعدة المادة المظلمة الباردة ، على سبيل المثال ، اعتماد
Tully-Fisher ، أو القدرة الغريبة للمادة المظلمة على تتبع توزيع المادة. لهذه الملاحظات ، لا يوجد تفسير مرضٍ يستند إلى نظريات معروفة. يفسر تعديل الجاذبية بعضها بنجاح ، لكنه يثير مشاكل أخرى. الكثير للأزمة! وهذه أزمة جيدة ، أجرؤ على القول ، لأن لدينا بيانات تتحسن كل يوم.
هذه ليست مشكلة مراقبة الأزمات الجيدة الوحيدة الموجودة في أساسيات الفيزياء. واحدة من أقدم ، ولكن لا تزال على قيد الحياة وبصحة جيدة ، هي
اللحظة المغناطيسية للميون . لدينا تناقض طويل الأمد بين التنبؤات والقياسات النظرية ، والتي لم يتم حلها بعد. يعتبر العديد من المنظرين هذا إشارة إلى أنه لا يمكن تفسيره في إطار النموذج القياسي ، وبالتالي هناك حاجة إلى نظرية جديدة ومحسنة.
هناك زوجان من المشاكل المماثلة ، ومستمرة إلى حد ما. على سبيل المثال ، تجربة
DAMA . في هذه التجربة ، يبحث العلماء عن المادة المظلمة. يتلقون إشارة من مصدر غير معروف مع تعديل سنوي ، ويتابعونها لأكثر من عشر سنوات. هناك بالتأكيد إشارة ، ولكن إذا اتضح أنها مادة مظلمة ، فستتعارض النتيجة مع النتائج التجريبية الأخرى. ونتيجة لذلك ، ترى DAMA شيئًا ، ولكن لا أحد يعرف ما هو بالضبط.
لا تزال هناك ملاحظات محيرة من تجربة
LSND على تذبذبات النيوترينو التي لا تتوافق مع أي مجموعة أخرى من المعلمات. هناك أيضًا تناقض غريب في نتائج قياسات نصف قطر البروتون باستخدام طريقتين مختلفتين ، بالإضافة إلى
قصة أخرى مماثلة
مع عمر النيوترون . كانت هناك أيضًا بعض التناقضات في قياس معلمة هابل باستخدام طرق مختلفة ، وقد لا يستحق ذلك ، ولكن قد يكون من المفيد القلق بشأنه.
بالطبع ، قد يكون لكل من هذه الحالات الشاذة في البيانات تفسير "عادي". قد يكون هذا خطأ قياس منهجي أو خطأ حسابي أو عنصر مفقود مفقود. ولكن ربما ، ربما هذا شيء أكثر.
هذا نوع من "مشكلة الأزمة" - الصراع بين النظرية والملاحظة. ولكن إلى جانب هذه ، هناك مشاكل أزمات من نوع مختلف تمامًا ، تقع على جانب تطور النظريات. هذه مشاكل الاتساق الداخلي.
تنشأ مشكلة الاتساق الداخلي عندما تتنبأ نظريتك بملاحظات متضاربة أو غامضة أو لا معنى لها. من الأمثلة النموذجية على ذلك الاحتمالات التي تصبح أكبر من الوحدة ، والتي لا تتزامن مع تفسير الاحتمال. وبسبب هذه المشكلة ، اقتنع الفيزيائيون بأن المصادم LHC سيظهر لنا فيزياء جديدة. لم يعرفوا ما إذا كان سيكون هيجز ، ويمكن أن يكون شيئًا آخر - على سبيل المثال ، تغيير غير متوقع في التفاعل النووي الضعيف - ولكن اتضح أنه هيجز. أدت استعادة الاتساق الداخلي إلى توقع ناجح.
تاريخياً ، أدت دراسة قضايا الاتساق إلى العديد من الإنجازات المذهلة.
ومن الأمثلة على هذه المشكلة "
الكارثة فوق البنفسجية " التي يتعين على مصدر الحرارة أن ينبعث منها كمية لا حصر لها من الضوء عند أطوال موجية قصيرة. من الواضح أن هذا لا يتوافق مع النظرية الفيزيائية ذات المغزى التي يجب أن تكون الكميات المرصودة محدودة. (لاحظ أن هذا الصراع ينشأ مع الافتراض. رياضيا ، لا حرج في اللانهاية). قام Planck بحل هذه المشكلة ، وأدى الحل في النهاية إلى تطوير ميكانيكا الكم.
مشكلة أخرى مشهورة في الاتساق هي أن ميكانيكا نيوتن تبين أنها غير متوافقة مع تناظر الديناميكا الكهربائية الزمانية. حسم أينشتاين هذا الخلاف وتلقى نظرية خاصة للنسبية. قام ديراك لاحقًا بحل التناقض بين ميكانيكا الكم و STR ، مما أدى إلى إنشاء نظرية المجال الكمومي. أزال أينشتاين التناقضات الإضافية بين SRT والجاذبية النيوتونية ، وتلقى GR.
تم تحديد جميع هذه المشاكل وتحديدها بشكل جيد.
لكن معظم المشكلات النظرية الحالية في أساسيات الفيزياء ليست من هذا النوع. نعم ، سيكون من الجميل إذا تم دمج التفاعلات الثلاثة للنموذج القياسي في واحد. سيكون ذلك لطيفًا ، لكن هذا ليس ضروريًا لتحقيق الاتساق. نعم ، سيكون من الجميل لو كان الكون فائق التناظر. سيكون ذلك لطيفًا ، لكن هذا ليس ضروريًا لتحقيق الاتساق. نعم ، سيكون من الجميل لو شرحنا لماذا كتلة هيجز غير طبيعية من الناحية الفنية. لكن لا يوجد تناقض في حقيقة أن كتلة هيجز هي ما هي عليه.
حقيقة أن أينشتاين ، وحتى ديراك ، مستوحاة من جمال نظرياته موصوفة جيدًا. أحب ديراك بشكل خاص الإشادة باستخدام الأناقة الرياضية في تطوير النظريات. لكن دوافعهم الشخصية تهمنا بقدر ما. إذا نظرنا إلى الوراء ، فإننا نفهم أنهم نجحوا لأنهم قاموا في البداية بمهام جيدة.
هناك عدد قليل من المشاكل النظرية الحقيقية في أساسيات الفيزياء اليوم ، لكنها موجودة. واحد منهم هو عدم تحديد الجاذبية. من المستحيل رياضيًا تجميع النموذج القياسي والنسبية العامة معًا ، ولا نعرف كيفية القيام بذلك بشكل صحيح.
مشكلة خطيرة أخرى في النموذج القياسي هي
القطب Landau في أحد
ثوابت الاقتران . هذا يعني أن قوة أحد التفاعلات تصبح لانهائية. هذه ليست نتيجة مادية ، تمامًا مثل كارثة الأشعة فوق البنفسجية ، لذلك يجب أن يحدث شيء هنا. تم تكريس القليل من الاهتمام لهذه المشكلة ، حيث يعتقد معظم المنظرين أن النموذج القياسي متحد قبل الوصول إلى قطب لانداو ، مما يجعل الاستقراء غير ضروري.
لا تزال هناك حالات لا يتضح فيها نوع المهمة التي نتعامل معها. واحد منهم هو عدم التقارب في التوسع المضطرب. ربما يكون السؤال الوحيد هو تحسين الجهاز الرياضي ، أو ربما نسيء فهم نظرية المجال الكمي تمامًا. نفس الحالة مع
نظرية هاج . من الصعب بالنسبة لي أيضًا تصنيف
مشكلة القياس في ميكانيكا الكم. إن مناشدة العمليات الميكروسكوبية في بديهيات النظرية لا تتوافق مع مُثل الاختزاليين ، ولكن مرة أخرى ، هذه ليست مشكلة أساسية ، بل مصدر قلق مفاهيمي. لذا حول هذه المسألة أنا في وضع صعب.
ومع ذلك ، فإن الدرس الذي يعلمنا إياه تاريخ مشكلات الأزمات واضح: المشكلات موضوعات بحثية واعدة إذا كانت بالفعل مشاكل. أي يجب أن تكون قادرًا على صياغة تناقض رياضي. إذا كانت المشكلة ببساطة هي أنك لا تحب جانبًا معينًا من النظرية ، فمن المحتمل أن تضيع وقتك.