للتحقق من معادلات أينشتاين ، تحتاج إلى ركلة ثقب أسود

حقق فريقان من الباحثين تقدمًا كبيرًا في إثبات فرضية استقرار الثقوب السوداء ، وهو أهم اختبار رياضي لنظرية النسبية العامة لأينشتاين.

في نوفمبر 1915 ، في محاضرة في الأكاديمية البروسية للعلوم ، وصف ألبرت أينشتاين فكرة حولت الإنسانية حول الكون. بدلاً من أخذ هندسة المكان والزمان ثابتة ، أوضح أينشتاين أننا نعيش في واقع رباعي الأبعاد يسمى الزمكان ، الذي يتقلب شكله استجابة للمادة والطاقة.

وصف أينشتاين هذه الفكرة المهمة بالتفصيل في عدة معادلات تسمى " معادلات أينشتاين " (أو معادلات مجال الجاذبية) التي تشكل جوهر GTR له. تم تأكيد هذه النظرية من خلال جميع الاختبارات التجريبية التي خضعت لها في القرن المقبل.

وعلى الرغم من أن نظرية أينشتاين تبدو وكأنها تصف العالم المرصود ، إلا أن الرياضيات الأساسية تظل غامضة إلى حد كبير. تمكن علماء الرياضيات من تقديم أدلة قليلة جدًا بشأن المعادلات بأنفسهم. نحن نعلم أنها تعمل ، ولكن لا يمكننا تحديد السبب بالضبط. حتى آينشتاين كان عليه أن يعود إلى التقريب ، وليس إلى الحلول الدقيقة ، لرؤية الكون من خلال العدسات التي ابتكرها.

ولكن خلال العام الماضي ، وضع علماء الرياضيات الرياضيات الوراثية في بؤرة أوضح. توصلت مجموعتان إلى حلول تتعلق بمشكلة مهمة في الموارد الوراثية ، والمعروفة باسم فرضية استقرار الثقب الأسود. يثبت عملهم أن معادلات أينشتاين تتوافق مع الحدس الجسدي لسلوك الزمكان: إذا قمت بتطبيق اضطراب حاد عليه ، فسوف يذهل مثل الهلام ، ثم يهدأ في حالة مستقرة ، والتي بدأ منها كل شيء.

إذا كانت القرارات غير مستقرة ، فهذا يعني أنها ليست مادية. قال سيرجيو كلاينرمان ، عالم الرياضيات في جامعة برينستون ، والمؤلف ، إلى جانب جيريمي زفتيل ، لواحدة من نتيجتين: " سيكون شبحًا رياضيًا موجودًا في الرياضيات ، ولكن لا يهم من وجهة نظر الفيزياء".

لإكمال البراهين ، كان علماء الرياضيات بحاجة إلى حل التعقيد الأساسي لمعادلات أينشتاين. لوصف تطور شكل الزمكان ، أنت بحاجة إلى نظام إحداثيات - شيء مثل خطوط الطول والعرض - يخبرك بمكان وجود بعض النقاط. وفي الزمكان ، من الصعب جدًا العثور على نظام إحداثيات يعمل في كل مكان.

هز الثقب الأسود

كما تعلم ، فإن GR تصف الزمكان على أنه شيء مثل ورقة مطاطية. في حالة عدم وجود مادة ، تكون الورقة مسطحة. ابدأ في إسقاط الكرات عليه - النجوم والكواكب - وستتشوه الورقة. تدور الكرات تجاه بعضها البعض. عندما تتحرك الأشياء ، يتغير شكل الورقة المطاطية أيضًا في الاستجابة.

تصف معادلات أينشتاين تطور شكل الزمكان. أنت تقدم لهم معلومات حول الانحناء والطاقة في كل نقطة ، وتعطي شكل الزمكان في المستقبل. بهذا المعنى ، فإن معادلات أينشتاين تشبه أي معادلات تحاكي ظاهرة فيزيائية: هنا الكرة في الوقت صفر ، وهنا - بعد خمس ثوان.

قال بيتر هينز ، زميل باحث في معهد كلاي للرياضيات في جامعة كاليفورنيا في بيركلي ، المسؤول عن النتيجة الثانية مع أندراس فاسيا: "هذه نسخة كمية دقيقة من الناحية الحسابية للتأكيد على أن الزمكان منحني في وجود المادة".

في عام 1916 ، بعد إصدار GTR تقريبًا ، وجد الفيزيائي الألماني كارل شوارزشيلد حلاً دقيقًا للمعادلات التي تصف ما نعرفه الآن باسم ثقب أسود (ظهر هذا المصطلح بعد خمسة عقود فقط ). في وقت لاحق ، وجد الفيزيائيون حلولًا دقيقة تصف الثقب الأسود الدوار و BH بشحنة كهربائية.

وهذه كلها قرارات دقيقة تصف BH. إذا قمت بإضافة BH ثانية على الأقل ، فإن تفاعل القوى يصبح معقدًا للغاية بالنسبة للرياضيات الحديثة بحيث يتعامل معها فقط في حالات خاصة جدًا.

ومع ذلك ، لا يزال بإمكاننا طرح أسئلة مهمة حول هذه المجموعة المحدودة من الحلول. طرح أحد هذه الأسئلة في عام 1952 نتيجة لعمل عالم الرياضيات الفرنسي إيفون شوكيه بروهات. في الواقع ، يبدو هذا: ماذا يحدث إذا هزت ثقبًا أسود؟


إذا هزت BH ، فسوف يخلق موجات الجاذبية. لإثبات فرضية الاستقرار هي نفسها لإثبات أن هذه الموجات تنتشر في الفراغ ، مثل الموجات على سطح البركة بعد سقوط الحجر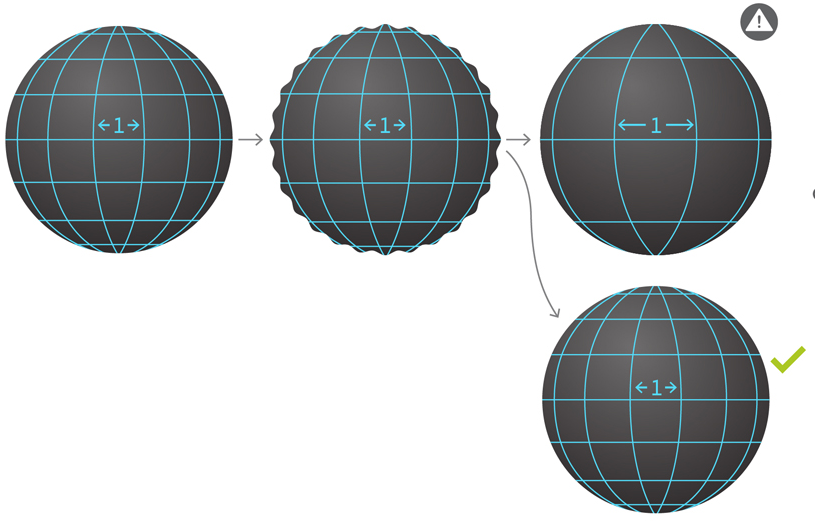


يتغير الزمكان بمرور الوقت ، وتتغير الشبكة المستخدمة لقياس الموجات الرطبة معه. يحدد القالب التغييرات على الشبكة ، ويجب تحديده بشكل صحيح. لنفترض أن لدينا مساحة مكانية بشبكة طولها 1 سم مرتبطة بنمط معين. سنشوش الزمكان حتى تظهر موجات الجاذبية. يمكن أن يتسبب نمط تم تحديده بشكل غير صحيح في تغيير مسافات الشبكة ، وسيبدو أن الموجات لا تضعف. يعد النمط الصحيح أمرًا حاسمًا لقياس العودة إلى الاستدامة.

تُعرف هذه المشكلة بفرضية استقرار BH. وتتوقع أن حلول معادلات أينشتاين ستكون "مستقرة في ظل الاضطرابات". بشكل غير رسمي ، إذا صدمت BH ، فستصبح المساحة أيضًا أكثر تكلفة أولاً ، ثم في التوغا ستهدأ في شكل سيبدو مشابهًا جدًا لما بدأنا به. قال كلينرمان: "على وجه التقريب ، تعني الاستدامة أنه إذا اتخذنا حلولًا خاصة وقمنا بغضبها قليلاً ، وقمنا بتغيير البيانات ، فإن الديناميكيات النهائية ستكون قريبة جدًا من الحل الأصلي".

ما يسمى "الاستقرار" هو اختبار مهم لأي نظرية فيزيائية. لفهم ذلك ، سيكون من المفيد تقديم مثال مألوف أكثر من BH.

تخيل بركة. تخيل الآن أنك رفعت سطحه بإلقاء حجر هناك. البركة مضطربة قليلاً ، ثم تهدأ. رياضيا ، يجب أن تصف حلول المعادلات المستخدمة لوصف البركة (في هذه الحالة ، معادلات Navier-Stokes ) هذه الصورة المادية الأساسية. إذا لم يتزامن الحل الأصلي مع القرار في المستقبل البعيد ، فقد تتساءل عن صحة معادلاتك.

قال فاسيا: "يمكن أن يكون للمعادلة أي خواص ، يمكن أن تكون صحيحة رياضياً ، لكن إذا كانت تتعارض مع التوقعات الجسدية ، فلا يمكن أن تكون صحيحة".


بيتر هينز ، عالم الرياضيات بجامعة كاليفورنيا

بالنسبة للرياضيين الذين يعملون على معادلات أينشتاين ، كان من الصعب العثور على دليل على الاستقرار أكثر من حلول المعادلات نفسها. ضع في اعتبارك حالة مساحة Minkowski المسطحة - وهي أبسط تكوينات الزمكان. تم اكتشاف هذا الحل لمعادلات آينشتاين في عام 1908 ، في سياق نظرية النسبية الخاصة لآينشتاين السابقة. ولكن فقط في عام 1993 ، كان علماء الرياضيات قادرين على إثبات أنه إذا هزت الزمان المسطح والفارغ ، فستحصل مرة أخرى على الزمان المسطح والفارغ. هذه النتيجة ، التي حصل عليها كلاينرمان وديميتريوس كريستودولو ، هي عمل موقر في هذا المجال.

ترتبط إحدى الصعوبات الرئيسية في إثبات الاستقرار بتتبع ما يحدث في الزمكان رباعي الأبعاد أثناء تطور الحل. تحتاج إلى نظام إحداثيات يسمح لك بقياس المسافات وتحديد النقاط في الزمكان ، مثل خطوط الطول والعرض ، المستخدمة لتحديد موقع على الأرض. ولكن ليس من السهل العثور على نظام إحداثيات يعمل في كل نقطة زمنية ، ويستمر في العمل عندما يتغير شكل الزمكان.

قال هينز في رسالة بريد إلكتروني: "لا نعرف طريقة للقيام بذلك ، وهي مناسبة لجميع الحالات". "الكون لا يعطينا نظام إحداثيات مفضل".

مشكلة القياس

أول شيء يجب فهمه حول أنظمة الإحداثيات هو أن الناس اخترعوها. الثاني - ليس كل نظام إحداثيات يسمح لك بتحديد جميع النقاط في الفضاء.

خذ خط العرض وخط الطول: يمكن تعيينهما بشكل تعسفي. يمكن لرسامي الخرائط اختيار أي خط وهمي كخط الطول الرئيسي. وعلى الرغم من أن خطوط الطول والعرض تساعد في تحديد أي مكان تقريبًا على الأرض ، إلا أنها لم تعد منطقية في القطبين الشمالي والجنوبي. إذا لم تكن تعرف شيئًا عن الأرض ، ولم يكن لديك سوى قراءات لخط العرض وخط الطول على يديك ، فيمكنك أن تستنتج بشكل خاطئ أن شيئًا ما هو خطأ طوبولوجي يحدث في هذه النقاط.

هذا الاحتمال - لاستخلاص استنتاجات غير صحيحة حول خصائص الفضاء المادي بسبب عدم كفاية نظام الإحداثيات الذي يصفه - هو جوهر السبب الذي يجعل من الصعب للغاية إثبات استقرار الزمكان.

قال ميكاليس دافرموس ، عالم الرياضيات في جامعة كامبريدج ، المتخصص البارز في دراسة معادلات أينشتاين: "قد يكون هذا الاستقرار موجودًا ، لكننا نستخدم إحداثيات غير مستقرة ، وبالتالي نتجاهل حقيقة الاستقرار".

في سياق نظرية استقرار الثقب الأسود ، يجب أن يتطور أي نظام إحداثيات مستخدم بنفس الطريقة التي يتطور بها شكل الزمكان - مثل القفاز المريح يتكيف مع تغيير شكل اليد. يجب أن تكون المراسلات بين نظام الإحداثيات والزمكان جيدة في البداية وأن تظل جيدة على طول الطريق. إذا لم يكن الأمر كذلك ، فيمكن أن يحدث شيئان يتعارضان مع محاولات إثبات وجود الاستقرار.


سيرجيو كلاينرمان ، عالم الرياضيات بجامعة برينستون

أولاً ، يمكن أن يغير نظام الإحداثيات الخاص بك شكله ، والذي سينكسر عند نقاط معينة ، تمامًا مثل توقف خطوط الطول والعرض عن العمل في القطبين. وتسمى هذه النقاط "التفردات المنسقة" (لتمييزها عن التفردات المادية ، على سبيل المثال ، الثقوب السوداء). هذه نقاط غير محددة في نظام الإحداثيات التي لا تسمح بالوصف الكامل لتطوير الحل حتى النهاية.

ثانيًا ، يمكن لنظام الإحداثيات الذي تم اختياره بشكل سيئ أن يخفي الظاهرة المادية التي يجب قياسها. لإثبات أن حلول معادلات أينشتاين تأتي إلى حالة هادئة بعد الاضطرابات ، يحتاج علماء الرياضيات إلى مراقبة تموجات الزمكان التي تسببها الاضطرابات بعناية. لفهم سبب ضرورة ذلك ، يجدر العودة مرة أخرى إلى القياس مع البركة. حجر يلقى في بركة يولد موجات. ينبع استقرار البركة على المدى الطويل من حقيقة أن الأمواج تضعف بمرور الوقت - تصبح أصغر وأصغر ، حتى لا يكون هناك أي أثر لوجودها.

الوضع مشابه للزمكان. سيؤدي الاضطراب إلى سلسلة من موجات الجاذبية ، ولإثبات الاستقرار ، من الضروري إثبات أن هذه الموجات موهنة. ولهذا ، هناك حاجة إلى نظام إحداثيات أو "شبكة" لقياس حجم الأمواج. تسمح الشبكة الصحيحة لعلماء الرياضيات برؤية كيف تتسطح الموجات وتختفي إلى الأبد.

قال كلاينرمان: "يجب تخفيف التوهين بالنسبة لشيء ما ، وهنا تأتي مشكلة الشبكة". "إذا أخذنا الشبكة الخاطئة ، فعندئذ حتى لو كان الاستقرار موجودًا ، فلا يمكن إثبات ذلك ، لأن الشبكة لن تظهر لي التوهين". وإذا لم تحسب معدل توهين الأمواج ، فمن المستحيل إثبات الاستقرار ".

المشكلة هي أنه على الرغم من أن نظام الإحداثيات مهم للغاية ، إلا أنه ليس من الواضح أي نظام سيختار. قال هينز: "هناك الكثير من الحرية في اختيار الظروف لهذه الشبكة". ومعظم الخيارات ستكون خاطئة ».

في الطريق الى الهدف

يتطلب الدليل الكامل على استقرار الثقوب السوداء إثباتًا على أن جميع الحلول المعروفة لمعادلات أينشتاين لـ BHs (مع دوران الثقب الأسود ضمن حدود معينة) مستقرة بعد الاضطراب. من بين الحلول المعروفة حل Schwarzschild الذي يصف الزمكان لـ BH غير الدوارة ، ومجموعة Kerr من الحلول التي تصف تكوين الزمكان الذي لا يوجد فيه سوى BH دوار واحد (وخصائص هذا BH - الكتلة والزخم الزاوي - تختلف داخل عائلة الحلول) .

تقدمت كلتا النتيجتين الجديدتين جزئيًا نحو إثبات فرضية كاملة.

أثبت Hinz and Washi ، في ورقة نشرت على arxiv.org في عام 2016 ، أن الثقوب السوداء الدوارة ببطء مستقرة. لكن عملهم لا يغطي BHs الدورية بسرعة أكبر من عتبة معينة.

أيضا ، أدلةهم لديها العديد من الافتراضات حول طبيعة الزمكان. حدثت الفرضية الأصلية في مساحة مينكوفسكي ، وهي ليست مسطحة وفارغة فحسب ، بل لها أيضًا حجم معين. البرهان من Hintz و Vasya يحدث في مساحة دي سيتر ، حيث ينمو الزمكان مع التسارع إلى الخارج ، كما هو الحال في الكون الحقيقي. يؤدي تغيير المشهد إلى تبسيط المشكلة من وجهة نظر فنية ، ويمكن فهم ذلك عن طريق القياس: إذا رميت حجرًا في بركة متوسعة ، فسيتمدد التمدد الموجات وسيضعفون بشكل أسرع مما لو لم يتم توسيع البركة.

قال هينز: "نحن نتطلع إلى كون ذي توسع متسارع". "إنها تجعل المهمة أسهل قليلاً ، لأن هذه العملية تضعف موجات الجاذبية."

يتميز كلاينرمان وشيفتل بميزة مختلفة قليلاً. دليلهم ، الذي نُشر الجزء الأول منه في نوفمبر الماضي ، يتم في شوارزشيلد الزمكان - وهو أقرب إلى الحالة الأصلية والأكثر تعقيدًا للمشكلة. تثبت استقرار BH غير الدورية ، لكنها لا تتعلق بالقرارات التي تدور فيها. علاوة على ذلك ، فإنها تثبت استقرار BH فقط لفئة ضيقة من الاضطرابات - تلك التي تكون فيها موجات الجاذبية المتولدة متماثلة بطريقة معينة.

تقدم كلتا النتيجتين تقنيات جديدة لاختيار نظام الإحداثيات المناسب. يبدأ Hinz و Vasi بحل تقريبي للمعادلات بناءً على نظام إحداثيات تقريبي ، ويزيدان تدريجياً من دقة الإجابة ، حتى يصلان إلى حلول دقيقة وإحداثيات تتصرف بشكل جيد. يستخدم كلاينرمان وشيفتل نهجًا هندسيًا أكثر.

يحاول الفريقان الآن بناء دليل على الفرضية الكاملة بناءً على أساليبهما. يعتقد بعض خبراء المراقبين أن اليوم الذي يعمل فيه ليس بعيدًا.

قال دافيرموس: "أعتقد حقًا أن كل شيء الآن في مرحلة الصعوبات التقنية". "اتضح أنه لحل هذه المشكلة ، لم تعد هناك حاجة لأفكار جديدة." وشدد على أن البرهان النهائي يمكن أن يقدمه أي من الرياضيين العاملين على المشكلة في الوقت الراهن.

لمدة مائة عام ، كانت معادلات آينشتاين بمثابة تعليمات تجريبية موثوقة للكون. ربما يقترب علماء الرياضيات الآن من توضيح سبب عملهم بشكل جيد.