ترجمة كيفية جعل الآلات بمعنى البيانات الضخمة: مقدمة لخوارزميات التجميع .ألق نظرة على الصورة أدناه. هذه مجموعة من الحشرات (القواقع ليست حشرات ، لكننا لن نجد خطأ) من مختلف الأشكال والأحجام. الآن قم بتقسيمهم إلى عدة مجموعات وفقًا لدرجة التشابه. لا صيد. ابدأ بتجميع العناكب.
انتهى؟ على الرغم من عدم وجود حل "صحيح" هنا ، يجب أن تكون قد قسمت هذه المخلوقات إلى أربع
مجموعات . في عنقود واحد توجد عناكب ، في الثانية - زوج من القواقع ، في الثالث - الفراشات ، وفي الرابع - ثلاثي من النحل والدبابير.
أحسنت ، أليس كذلك؟ ربما يمكنك أن تفعل الشيء نفسه إذا كان هناك ضعف عدد الحشرات في الصورة. وإذا كان لديك الكثير من الوقت - أو الرغبة الشديدة في علم الحشرات - فربما تكون قد جمعت مئات الحشرات.
ومع ذلك ، بالنسبة للآلة ، فإن تجميع عشرة أشياء في مجموعات ذات معنى ليست مهمة سهلة. بفضل هذا الفرع المعقد من الرياضيات مثل
التوافقية ، نعلم أن 10 حشرات مجمعة في 115،975 طريقة. وإذا كان هناك 20 حشرة ، فإن عدد خيارات التجميع
سيتجاوز 50 تريليون .
مع مائة حشرة ، سيكون عدد الحلول الممكنة أكبر من
عدد الجسيمات الأولية في الكون المعروف . كم أكثر؟ حسب تقديراتي ، حوالي
خمسمائة مليون مليار مرة . اتضح أكثر من
أربعة ملايين مليار من حلول
جوجل (
ما هو جوجل؟ ). وهذا فقط لمئات الأشياء.
ستكون كل هذه التركيبات تقريبًا بلا معنى. على الرغم من عدد الحلول التي لا يمكن تصورها ، فقد وجدت نفسك سريعًا جدًا إحدى الطرق المفيدة القليلة للتجميع.
نحن البشر نعتبر من المسلم به قدرتنا الممتازة على فهرسة وفهم كميات كبيرة من البيانات. لا يهم ما إذا كان نصًا ، أو صورًا على الشاشة ، أو سلسلة من الأشياء - يفهم الناس بشكل عام بشكل فعال البيانات القادمة من العالم المحيط.
بالنظر إلى أن أحد الجوانب الرئيسية لتطوير الذكاء الاصطناعي والتعلم الآلي هو أن الأجهزة يمكنها أن تفهم بسرعة كميات كبيرة من بيانات الإدخال ، كيف يمكنني تحسين كفاءة العمل؟ في هذه المقالة ، سننظر في ثلاث خوارزميات تجميع يمكن للآلات من خلالها استيعاب كميات كبيرة من البيانات بسرعة. هذه القائمة بعيدة عن الاكتمال - هناك خوارزميات أخرى - ولكن من الممكن بالفعل البدء بها.
بالنسبة لكل خوارزمية ، سأصف متى يمكن استخدامها ، وكيف تعمل ، وسأعطي أيضًا مثالًا مع التحليل خطوة بخطوة. أعتقد أنه من أجل فهم حقيقي للخوارزمية ، تحتاج إلى تكرار عملها بنفسك. إذا كنت
مهتمًا حقًا ، فستدرك أنه من الأفضل تشغيل الخوارزميات على الورق. تصرف ، لن يلومك أحد!
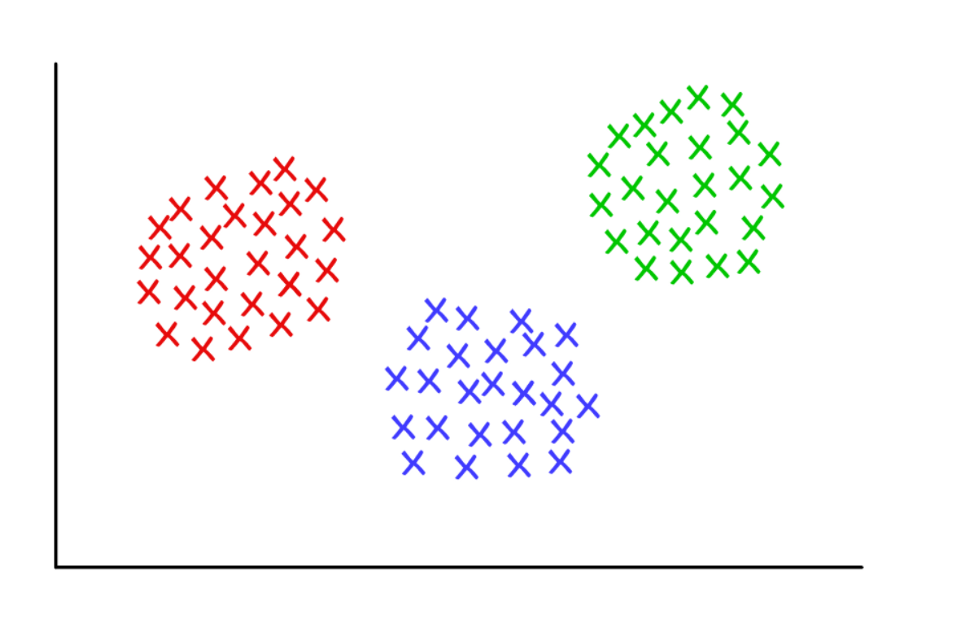ثلاث مجموعات مرتبة بشكل مثير للريبة مع k = 3K- تعني التكتل
مستخدم بواسطة:
عندما تفهم عدد المجموعات التي يمكن الحصول عليها للعثور
على محدد مسبقًا (بداهة).
كيف يعمل:
تقوم الخوارزمية بتعيين كل ملاحظة بشكل عشوائي إلى إحدى فئات
k ، ثم تقوم بحساب
المتوسط لكل فئة. ثم يعيد تعيين كل ملاحظة للفئة مع أقرب متوسط ، ويحسب المتوسطات مرة أخرى. تتكرر العملية حتى تكون هناك حاجة إلى إعادة التكليف.
مثال عملي:
خذ مجموعة من 12 لاعبًا وعدد الأهداف التي سجلها كل منهم في الموسم الحالي (على سبيل المثال ، في النطاق من 3 إلى 30). نقسم اللاعبين ، على سبيل المثال ، إلى ثلاث مجموعات.
الخطوة 1 : تحتاج إلى تقسيم اللاعبين عشوائيًا إلى ثلاث مجموعات وحساب المتوسط لكل منهم.
Group 1 Player A (5 goals), Player B (20 goals), Player C (11 goals) Group Mean = (5 + 20 + 11) / 3 = 12 Group 2 Player D (5 goals), Player E (3 goals), Player F (19 goals) Group Mean = 9 Group 3 Player G (30 goals), Player H (3 goals), Player I (15 goals) Group Mean = 16
الخطوة 2 : إعادة تعيين كل لاعب في المجموعة بأقرب متوسط. على سبيل المثال ، اللاعب أ (5 أهداف) يذهب إلى المجموعة 2 (المتوسط = 9). ثم مرة أخرى نحسب متوسطات المجموعة.
Group 1 (Old Mean = 12) Player C (11 goals) New Mean = 11 Group 2 (Old Mean = 9) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) New Mean = 4 Group 3 (Old Mean = 16) Player G (30 goals), Player I (15 goals), Player B (20 goals), Player F (19 goals) New Mean = 21
كرر الخطوة 2 مرارًا وتكرارًا حتى يتوقف اللاعبون عن تغيير المجموعات. في هذا المثال المصطنع ، سيحدث هذا في التكرار التالي.
توقف! لقد قمت بتشكيل ثلاث مجموعات من مجموعة بيانات!
Group 1 (Old Mean = 11) Player C (11 goals), Player I (15 goals) Final Mean = 13 Group 2 (Old Mean = 4) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) Final Mean = 4 Group 3 (Old Mean = 21) Player G (30 goals), Player B (20 goals), Player F (19 goals) Final Mean = 23
يجب أن تتوافق المجموعات مع موقع اللاعبين في الميدان - المدافعون والمدافعون المركزيون والمهاجمون. يعني K- العمل في هذا المثال لأنه يوجد سبب للاعتقاد بأن البيانات سيتم تقسيمها إلى هذه الفئات الثلاث.
وبالتالي ، بناءً على الاختلاف الإحصائي في الأداء ، يمكن للآلة تبرير موقع اللاعبين في الميدان لأي رياضة جماعية. هذا مفيد للتحليلات الرياضية ، وكذلك لأية مهام أخرى يساعد فيها تقسيم مجموعة البيانات إلى مجموعات محددة مسبقًا على استخلاص الاستنتاجات المناسبة.
هناك العديد من الاختلافات في الخوارزمية الموصوفة. يمكن إجراء التكوين الأولي للمجموعات بطرق مختلفة. درسنا التصنيف العشوائي للاعبين في مجموعات ، متبوعًا بحساب المتوسطات. ونتيجة لذلك ، فإن متوسطات المجموعة الأولية قريبة من بعضها البعض ، مما يزيد من التكرار.
طريقة بديلة هي تكوين مجموعات تتكون من لاعب واحد فقط ، ثم تجميع اللاعبين في أقرب مجموعات. تعتمد المجموعات الناتجة بشكل أكبر على المرحلة الأولية من التكوين ، وتقل إمكانية التكرار في مجموعات البيانات ذات التباين العالي. ولكن مع هذا النهج ، قد يستغرق الأمر تكرارًا أقل لإكمال الخوارزمية ، لأنه سيتم قضاء وقت أقل في تقسيم المجموعات.
العيب الواضح للمجموعات يعني أنك بحاجة
إلى التخمين
المسبق لعدد المجموعات لديك. هناك طرق لتقييم مطابقة مجموعة معينة من العناقيد. على سبيل المثال ، يعد مجموع المربعات داخل الكتلة مقياسًا للتنوع داخل كل مجموعة. كلما كانت الكتل "أفضل" ، انخفض مجموع المربعات داخل المجموعة.
المجموعات الهرمية
مستخدم بواسطة:
عندما تحتاج إلى الكشف عن العلاقة بين القيم (الملاحظات).
كيف يعمل:
يتم حساب مصفوفة المسافة التي تكون فيها قيمة الخلية (
i، j ) هي مقياس المسافة بين قيم
i و
j . ثم يتم أخذ زوج من القيم الأقرب ويتم حساب المتوسط. يتم إنشاء مصفوفة مسافة جديدة ، يتم دمج القيم المزدوجة في كائن واحد. ثم يتم أخذ زوج من القيم الأقرب من هذه المصفوفة الجديدة ويتم حساب قيمة متوسط جديدة. تتكرر الدورة حتى يتم تجميع كل القيم.
مثال عملي:
خذ مجموعة بيانات مبسطة للغاية مع عدة أنواع من الحيتان والدلافين. أنا عالم أحياء ، ويمكنني أن أؤكد لك أنه يتم استخدام المزيد من الخصائص لبناء
أشجار وراثية . لكن على سبيل المثال ، نحن نقتصر على طول الجسم المميز لستة أنواع من الثدييات البحرية. ستكون هناك مرحلتان من الحسابات.
الخطوة 1 : يتم حساب مصفوفة المسافات بين جميع المشاهدات. سنستخدم مقياس الإقليدية الذي يصف مدى بُعد بياناتنا عن بعضها البعض ، مثل المستوطنات على الخريطة. يمكنك الحصول على الفرق في طول أجسام كل زوج من خلال قراءة القيمة عند تقاطع العمود والصف المقابل.
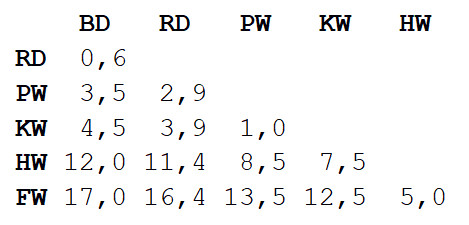الخطوة 2 : خذ نوعين قريبين من بعضهما البعض. في هذه الحالة ، هو دلفين قاروري ودلفين رمادي ، حيث يبلغ متوسط طول الجسم 3.3 م.
نكرر الخطوة 1 ، ونحسب مصفوفة المسافة مرة أخرى ، ولكن هذه المرة ندمج دلفين الزجاجة والدلفين الرمادي في كائن واحد بطول الجسم 3.3 م.
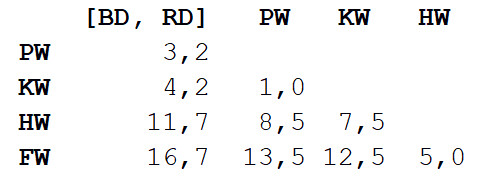
نكرر الآن الخطوة 2 ، ولكن بمصفوفة مسافة جديدة. هذه المرة سيكون الحوت القاتل هو الأقرب ، لذلك دعونا نضعها في زوجين ونحسب المتوسط - 7 م.
بعد ذلك ، كرر الخطوة 1: مرة أخرى ، احسب مصفوفة المسافة ، ولكن مع الحوت طحن والقاتل في شكل كائن واحد بطول الجسم 7 م.
كرر الخطوة 2 مع هذه المصفوفة. ستكون أصغر مسافة (3.7 م) بين الكائنين مجتمعين ، لذلك سنقوم بدمجهما في كائن أكبر وحساب متوسط القيمة - 5.2 م.
ثم كرر الخطوة 1 وحساب مصفوفة جديدة من خلال الجمع بين دلفين الزجاجة / الدلفين الرمادي مع حوت طحن / قاتل.
كرر الخطوة 2. ستكون أصغر مسافة (5 أمتار) بين الحدباء والقصيص ، لذلك نجمعها ونحسب المتوسط - 17.5 م.
مرة أخرى الخطوة 1: حساب المصفوفة.
أخيرًا ، كرر الخطوة 2 - لا يوجد سوى مسافة واحدة متبقية (12.3 م) ، لذلك سنوحد الجميع في كائن واحد ونتوقف. إليك ما حدث:
[[[BD, RD],[PW, KW]],[HW, FW]]
يحتوي الكائن على هيكل هرمي (تذكر
JSON ) ، لذلك يمكن عرضه على شكل رسم بياني شجري أو مخطط شريطي. والنتيجة مشابهة لشجرة العائلة. كلما كانت القيمتان أقرب إلى الشجرة ، كلما كانتا متشابهتين أو أكثر ارتباطًا.
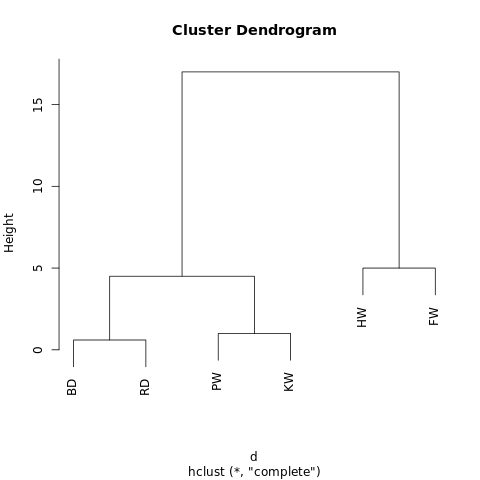تم إنشاء مخطط شريطي بسيط باستخدام R-Fiddle.orgتسمح لك بنية مخطط الشجرة بفهم بنية مجموعة البيانات نفسها. في مثالنا ، حصلنا على فرعين رئيسيين - أحدهما مع حدباء وزعانف ، والآخر مع دلفين قاروري / دلفين رمادي وحوت طحن / قاتل.
في علم الأحياء التطوري ، يتم استخدام مجموعات بيانات أكبر بكثير مع العديد من الأنواع ووفرة الشخصيات لتحديد العلاقات التصنيفية. خارج علم الأحياء ، يتم تطبيق التجميع الهرمي في مجالات تعدين البيانات والتعلم الآلي.
لا يتطلب هذا النهج التنبؤ بالعدد المطلوب من العناقيد. يمكنك تقسيم مخطط الشظية الناتج إلى مجموعات ، "تقليم" الشجرة عند الارتفاع المطلوب. يمكنك اختيار الارتفاع بطرق مختلفة ، اعتمادًا على الدقة المطلوبة لتجميع البيانات.
على سبيل المثال ، إذا تم قطع مخطط الشريان أعلاه على ارتفاع 10 ، فسوف نتقاطع بين الفرعين الرئيسيين ، وبالتالي نقسم مخطط الشريان إلى عمودين. إذا تم قطعه على ارتفاع 2 ، فقم بتقسيم مخطط الشريان إلى ثلاث مجموعات.
قد تختلف خوارزميات التجميع الهرمي الأخرى في ثلاثة جوانب عن تلك الموضحة في هذه المقالة.
أهم شيء هو النهج. استخدمنا هنا طريقة
التكتل : بدأنا بقيم فردية وقمنا بتجميعها دوريًا حتى حصلنا على مجموعة كبيرة واحدة. ينطوي النهج البديل (والأكثر تعقيدًا من الناحية الحسابية) على التسلسل العكسي: أولاً يتم إنشاء مجموعة ضخمة واحدة ، ثم يتم تقسيمها بالتسلسل إلى مجموعات أصغر من أي وقت مضى حتى تبقى قيم منفصلة.
هناك أيضًا عدة طرق لحساب مصفوفات المسافة. المقاييس الإقليدية كافية لمعظم المهام ، ولكن
المقاييس الأخرى مناسبة بشكل أفضل في بعض المواقف.
أخيرًا ، قد يختلف معيار الربط. تعتمد العلاقة بين العناقيد على قربها من بعضها البعض ، ولكن تعريف "التقارب" يمكن أن يكون مختلفًا. في مثالنا ، قمنا بقياس المسافة بين متوسط القيم (أو "centroids") لكل مجموعة وجمعنا أقرب المجموعات في أزواج. ولكن يمكنك استخدام تعريف آخر.
افترض أن كل عنقود يتكون من عدة قيم منفصلة. يمكن تعريف المسافة بين مجموعتين بأنها المسافة الدنيا (أو القصوى) بين أي من قيمها ، كما هو موضح أدناه. بالنسبة إلى السياقات المختلفة ، من المناسب استخدام تعريفات مختلفة لمعيار الصلة.
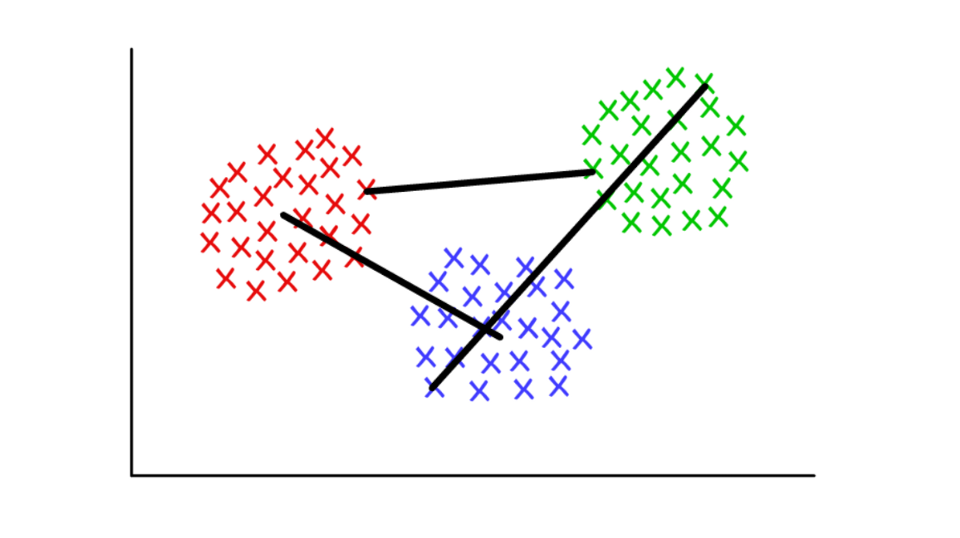أحمر / أزرق: مسبح مركزي. أحمر / أخضر: الجمع على أساس الحد الأدنى ؛ أخضر / أزرق: الدمج على أساس الارتفاعات.تعريف المجتمعات في الرسوم البيانية (اكتشاف مجتمع الرسم البياني)
مستخدم بواسطة:
متى يمكن تقديم بياناتك في شكل شبكة أو "رسم بياني".
كيف يعمل:
يمكن تعريف
المجتمع في الرسم البياني تقريبًا على أنه مجموعة فرعية من القمم التي ترتبط ببعضها البعض أكثر من بقية الشبكة. هناك خوارزميات مختلفة لتعريف المجتمع تستند إلى تعريفات أكثر تحديدًا ، مثل Edge Betweenness و Modularity-Maximsation و Walktrap و Clique Percolation و Leading Eigenvector ...
مثال عملي:
نظرية الرسم البياني هي فرع مثير للاهتمام للغاية من الرياضيات يسمح لنا بنمذجة النظم المعقدة في شكل مجموعات مجردة من "النقاط" (الذروات ، العقد) متصلة بـ "خطوط" (حواف).
ربما يكون أول تطبيق للرسومات التي تتبادر إلى الذهن هو دراسة الشبكات الاجتماعية. في هذه الحالة ، تمثل القمم الأشخاص الذين تربطهم الأضلاع بالأصدقاء / المشتركين. ولكن يمكنك أن تتخيل أي نظام على شكل شبكة إذا كان بإمكانك تبرير طريقة الاتصال المجدي للمكونات. تشمل التطبيقات المبتكرة للتكتلات باستخدام نظرية الرسم البياني استخراج الخصائص من البيانات المرئية وتحليل الشبكات التنظيمية الجينية.
كمثال بسيط ، لنلق نظرة على الرسم البياني أدناه. يوضح هذا المواقع الثمانية التي أزورها كثيرًا. الروابط بينهما مبنية على روابط في مقالات ويكيبيديا. يمكن جمع هذه البيانات يدويًا ، ولكن بالنسبة للمشاريع الكبيرة ، يكون كتابة نص Python أسرع بكثير. على سبيل المثال ، هذا:
https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py .
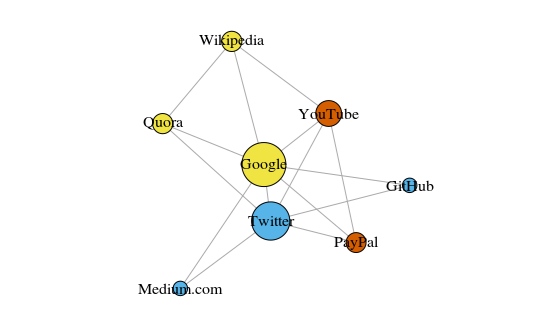تم بناء الرسم البياني باستخدام حزمة igraph لـ R 3.3.3يعتمد لون القمم على المشاركة في المجتمعات ، ويعتمد الحجم على المركزية. يرجى ملاحظة أن الأكثر مركزية هي Google و Twitter.
أيضًا ، تعكس المجموعات الناتجة بدقة شديدة المهام الحقيقية (وهذا دائمًا مؤشر مهم للأداء). يتم تمييز الذروات التي تمثل مواقع الارتباط / البحث باللون الأصفر ؛ المواقع المميزة باللون الأزرق للمنشورات عبر الإنترنت (المقالات أو التغريدات أو التعليمات البرمجية) ؛ أبرزت باللون الأحمر PayPal و YouTube ، التي أسسها موظفون سابقون في PayPal. خصم جيد للكمبيوتر!
بالإضافة إلى تصور الأنظمة الكبيرة ، تكمن القوة الحقيقية للشبكات في التحليل الرياضي. لنبدأ بتحويل صورة الشبكة إلى تنسيق رياضي. فيما يلي مصفوفة
المجاورة للشبكة.
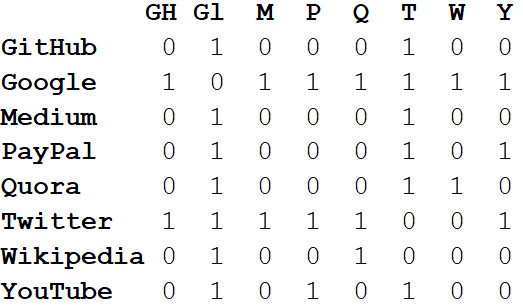
تشير القيم عند تقاطعات الأعمدة والصفوف إلى ما إذا كانت هناك حافة بين هذا الزوج من القمم. على سبيل المثال ، بين Medium و Twitter ، يكون عند تقاطع هذا السطر والعمود 1. وبين Medium و PayPal لا توجد حافة ، لذلك في الخلية المقابلة هناك 0.
إذا قمنا بتمثيل جميع خصائص الشبكة في شكل مصفوفة مجاورة ، فسيسمح لنا ذلك باستخلاص جميع أنواع الاستنتاجات المفيدة. على سبيل المثال ، مجموع القيم في أي عمود أو صف يميز
درجة كل قمة - أي عدد الكائنات المتصلة بهذا الرأس. يشار عادة بالحرف
ك .
إذا جمعنا درجات جميع القمم وقسمنا على اثنين ، نحصل على L - عدد الحواف في الشبكة. وعدد الصفوف والأعمدة يساوي N - عدد القمم في الشبكة.
من خلال معرفة k و L و N فقط والقيم الموجودة في جميع خلايا مصفوفة المجاورة A ، يمكننا حساب نموذجية أي تجمع.
لنفترض أننا قمنا بتجميع شبكة في عدد من المجتمعات. ثم يمكنك استخدام قيمة الوحدات النمطية للتنبؤ "بجودة" التكتل. تشير الوحدات النمطية الأعلى إلى أننا قسمنا الشبكة إلى مجتمعات "دقيقة" ، وتشير وحدات نمطية أقل إلى أن المجموعات تتشكل بالصدفة أكثر من المعقول. لتوضيح الأمر:
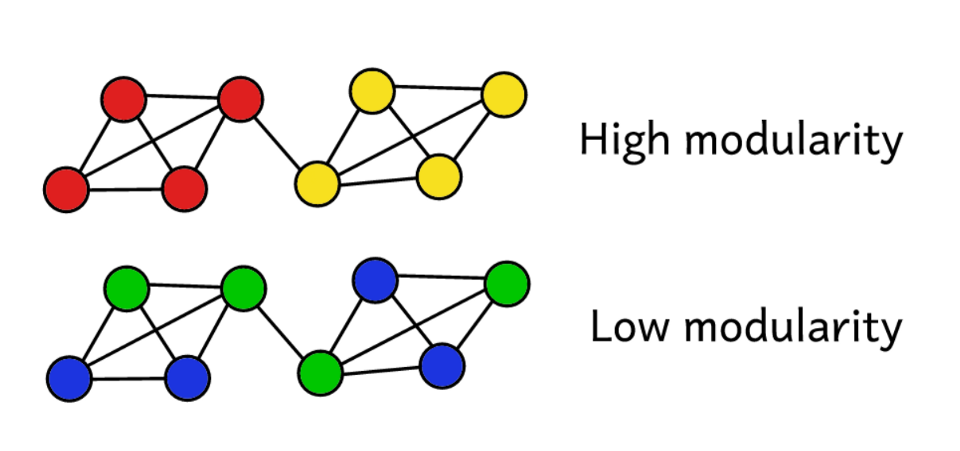
تعمل الوحدات النمطية كمقياس "لجودة" المجموعات.
يمكن حساب الوحدات النمطية باستخدام الصيغة التالية:
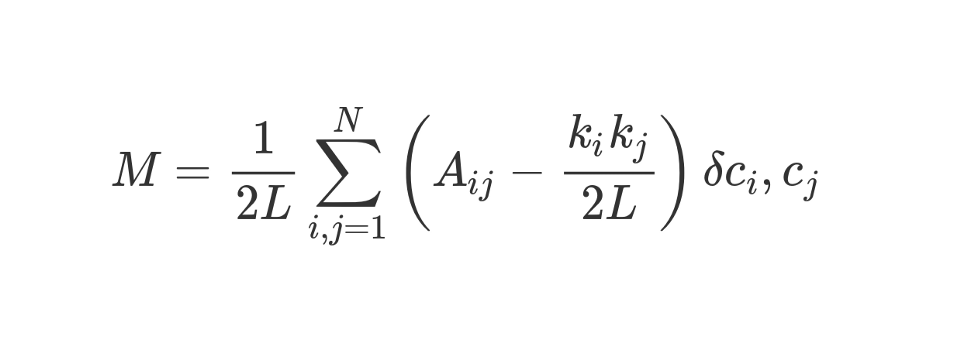
دعونا ننظر إلى هذه التركيبة الرائعة المظهر.
م ، كما تعلمون ، هذه نمطي.
يعني معامل
1/2 لتر أننا نقسم باقي "نص" الصيغة على 2 لتر ، أي على العدد المزدوج للحواف في الشبكة. في بيثون ، يمكن للمرء أن يكتب:
sum = 0 for i in range(1,N): for j in range(1,N): ans =
ما هو
#stuff with i and j ؟ تخبرنا البتات بين الأقواس بطرح (k_i k_j) / 2L من A_ij ، حيث A_ij هي القيمة في المصفوفة عند تقاطع الصف i والعمود j.
القيمتان k_i و k_j هي درجات كل قمة. يمكن العثور عليها عن طريق جمع القيم في الصف i والعمود j ، على التوالي. إذا قمنا بمضاعفتهم والقسمة على 2 لتر ، فإننا نحصل على العدد المتوقع من الحواف بين الذروتين i و j إذا كانت الشبكة مختلطة بشكل عشوائي.
تعكس محتويات الأقواس الفرق بين البنية الفعلية للشبكة والبنية المتوقعة إذا تم إعادة بناء الشبكة بشكل عشوائي. إذا كنت تتلاعب بالقيم ، فستكون أعلى الوحدات النمطية عند A_ij = 1 ومنخفضة (k_i k_j) / 2L. أي أن الوحدات النمطية تزداد إذا كانت هناك حافة "غير متوقعة" بين الذروتين i و j.
أخيرًا ، نضرب محتويات الأقواس بما يشار إليه في الصيغة كـ δc_i، c_j. هذه هي وظيفة Kronecker-delta. هنا هو تطبيقه في Python:
def Kronecker_Delta(ci, cj): if ci == cj: return 1 else: return 0 Kronecker_Delta("A","A")
نعم ، بهذه البساطة. تأخذ الدالة وسيطتين ، وإذا كانت متطابقة ، فإنها ترجع 1 ، وإذا لم تكن كذلك ، فعندئذٍ 0.
بمعنى آخر ، إذا كانت القمم i و j تقع في مجموعة واحدة ، فإن δc_i، c_j = 1. وإذا كانتا في مجموعات مختلفة ، فستُرجع الدالة 0.
نظرًا لأننا نضرب محتويات الأقواس برمز Kronecker ، فإن نتيجة المبلغ المستثمر be ستكون الأعلى عندما تكون القمم داخل مجموعة واحدة متصلة بعدد كبير من الحواف "غير المتوقعة". وبالتالي ، فإن الوحدات النمطية هي مؤشر على مدى جودة الرسم البياني في مجموعات فردية.
القسمة على 2L تحدد النموذجية العليا للوحدة. إذا كانت الوحدة النمطية قريبة من الصفر أو سلبية ، فهذا يعني أن التكتل الحالي للشبكة لا معنى له. من خلال زيادة الوحدات النمطية ، يمكننا العثور على طريقة أفضل لتجميع الشبكة.
يرجى ملاحظة أنه من أجل تقييم "جودة" تجميع الرسم البياني ، نحتاج إلى تحديد مسبق لكيفية تجميعها. لسوء الحظ ، ما لم تكن العينة صغيرة جدًا ، نظرًا للتعقيد الحسابي ، فمن المستحيل جسديًا الذهاب بغباء عبر جميع طرق تجميع الرسم البياني من خلال مقارنة نمطيتها.
تقترح
التوافقيات أنه بالنسبة لشبكة بها 8 رؤوس ، هناك 4140 طريقة تجميع. بالنسبة للشبكة التي تحتوي على 16 قمة ، سيكون هناك بالفعل أكثر من 10 مليار طريقة ، بالنسبة للشبكة التي تحتوي على 32 قمة ، و 128 septillion ، وللشبكة التي تحتوي على 80 قمة ، سيتجاوز
عدد طرق التجميع
عدد الذرات في الكون المرئي .
لذلك ، بدلاً من التعداد ، نستخدم الطريقة الإرشادية ، والتي ستساعد على حساب المجموعات بسهولة نسبيًا بأقصى حد من الوحدات النمطية. هذه خوارزمية تسمى
Fast-Greedy Modularity-Maximization ، وهي نوع من التناظرية لخوارزمية التجميع الهرمي التراكمي الموضحة أعلاه. بدلاً من الجمع على أساس القرب ، توحد Mod-Max المجتمعات اعتمادًا على التغييرات في الوحدات النمطية. كيف يعمل:
أولاً ، يتم تعيين كل قمة لمجتمعها الخاص ويتم حساب نمطية الشبكة بالكامل - M.
الخطوة 1 : لكل زوج من المجتمعات المتصلة بحافة واحدة على الأقل ، تحسب الخوارزمية التغيير الناتج في الوحدات النمطية ΔM في حالة الجمع بين أزواج المجتمعات هذه.
الخطوة 2 : ثم يتم أخذ زوج ، عندما يكون مجتمعة ، سيكون الحد الأقصى للميكرومتر ، ويتم دمجه. بالنسبة لهذه المجموعة ، يتم حساب وحدات نمطية جديدة وتخزينها.
تتكرر الخطوتان 1 و 2: في كل مرة ينضم فيها زوج من المجتمعات ، مما يعطي أكبر ميكرومتر ، مخطط تجمع جديد و M.
تتوقف التكرارات عندما يتم تجميع كل القمم في عنقود ضخم واحد. تقوم الخوارزمية الآن بفحص السجلات المخزنة وتجد مخطط التجميع بأعلى مستوى من الوحدات النمطية. هي التي تعود كهيكل مجتمعي.
لقد كانت صعبة حسابياً ، على الأقل بالنسبة للناس. نظرية الرسم البياني هي مصدر غني للمشاكل الحسابية الصعبة والمشاكل الصعبة NP. باستخدام الرسوم البيانية ، يمكننا استخلاص العديد من الاستنتاجات المفيدة حول الأنظمة ومجموعات البيانات المعقدة. اسأل لاري بيج ، الذي تعتمد خوارزمية PageRank الخاصة به - التي ساعدت Google على التحول من شركة ناشئة إلى شركة عالمية مهيمنة في أقل من جيل - على نظرية الرسم البياني.
تركز دراسات نظرية الرسم البياني اليوم على تحديد المجتمعات. هناك العديد من البدائل لخوارزمية Modularity-Maximization ، على الرغم من أنها مفيدة ، إلا أنها لا تخلو من عيوبها.
أولاً ، مع نهج التكتل ، غالبًا ما يتم دمج المجتمعات الصغيرة المحددة جيدًا في مجتمعات أكبر. يُسمى
هذا حد الدقة - لا تخصص الخوارزمية مجتمعات أصغر من حجم معين. عيب آخر هو أنه بدلاً من ذروة عالمية واضحة ويمكن تحقيقها بسهولة ، تسعى خوارزمية Mod-Max إلى إنشاء "هضبة" واسعة من العديد من قيم الوحدات النمطية القريبة. ونتيجة لذلك ، يصعب تحديد الفائز.
تستخدم الخوارزميات الأخرى طرقًا مختلفة لتحديد المجتمعات. على سبيل المثال ، Edge-Betweenness هي خوارزمية (فاصلة) للانقسام تبدأ من خلال تجميع كل القمم في مجموعة ضخمة واحدة. ثم تتم إزالة الحواف الأقل "أهمية" بشكل متكرر حتى يتم عزل جميع القمم. والنتيجة هي هيكل هرمي تتقارب فيه القمم من بعضها البعض ، وكلما تشابهت أكثر.
الخوارزمية ، Clique Percolation ، تأخذ في الاعتبار التقاطعات المحتملة بين المجتمعات. هناك مجموعة من الخوارزميات تعتمد على
المشي العشوائي على الرسم البياني ، وهناك طرق
تجميع طيفية تتعامل مع التحلل الطيفي (تكوين eigendecomposition) لمصفوفة المجاورة والمصفوفات الأخرى المشتقة منها. يتم استخدام كل هذه الأفكار لتسليط الضوء على الميزات ، على سبيل المثال ، في رؤية الماكينة.
لن نقوم بتحليل أمثلة عمل لكل خوارزمية بالتفصيل.
يكفي أن نقول أنه يتم اليوم إجراء بحث نشط في هذا الاتجاه ، ويتم إنشاء تقنيات قوية لتحليل البيانات ، والتي كان من الصعب للغاية حسابها قبل 20 عامًا.الخلاصة
, - , , . , , 20-40 .
, — , . , , .
, , , , . , - , , ? - !