نحسب احتمالات مقال "لعبة غير شريفة ، أو كيف يخدعنا منظمو السحب"

أثارت مقالة حول تحليل اللعبة من قبل شبكة تجارية معروفة اهتمامًا كبيرًا بـ Cloud4Y . فيما يلي بعض المقاطع التي تساعدك على تحقيق السرعة:

ذات مرة ، في صباح ربيعي مشمس ، قرأت منتدى المدينة ، صادفت رابطًا مع لعبة بسيطة من شبكة تجارية معروفة. كانت اللعبة (الحركة) المخصصة لكأس العالم عبارة عن ملعب غير معقد لثلاثة من ثلاثة حقول مليئة بكرات كرة القدم. من خلال النقر على الكرة ، فتحنا صورة بمنتج معين. عند فتح ثلاث صور متطابقة ، تم ضمان حصول المشترك على استلام مجاني لهذا المنتج في أحد متاجر الشبكة. أيضا ، تحت إحدى الكرات كانت هناك صورة لبطاقة حمراء ، يعني افتتاحها نهاية اللعبة.

بدأ كاتب المقال بالتحقيق في أسباب خسارته ، واستناداً إلى نتائج الحسابات ، اكتشف ما يلي:

رسم سريع للصيغ على منديل ، وتبين أن احتمال الفوز هو 1/4. في 5 حقول ، كان علي أن العبث ، ولكن الاحتمال المحسوب كان أيضًا 25 ٪.
...
عند تشغيل البرنامج النصي ، حصلت على نتيجة غير متوقعة - 25٪ من المكاسب. بعد أن لعبت مع عدد العناصر الفائزة وإجمالي عدد الحقول ، اكتشفت أن احتمال الفوز في مثل هذه اللعبة لا يعتمد على عدد الحقول ويساوي واحدًا مقسومًا على عدد العناصر الفائزة التي زادها حقل واحد.

كنا مهتمين بصحة مثل هذا الحساب ، واستبدال المنديل ببرنامج Excel ، بدأنا في العمل بحثًا عن الحقيقة الرياضية. القراء المولعون بنظرية الاحتمالات مدعوون للقطط من أجل التحقق من صحة حساباتنا.

بادئ ذي بدء ، نجد قواعد اللعبة. في هذا ، دون معرفة ذلك ، ساعد مستخدم Habr Stecenko في تعليقه . يكتب أيضًا:

إذا نظرت إلى نص المؤلف ، فهو مكتوب على افتراض أنه يجب أن يكون هناك ثلاث بطاقات لمنتج واحد في الميدان ، وبطاقة واحدة من خمس سلع أخرى ، وبطاقة حمراء واحدة ، في حين أن وصف اللعبة لا يتبع هذا على الإطلاق - القواعد لا تقول أن التركيبة الفائزة يجب أن تكون موجودة في الميدان.

ومع ذلك ، تنص القواعد على مشاركة ما مجموعه 26 منتجًا. اتضح أنه تم إنشاء إصدار 9 بطاقات: 8 بطاقات عبارة عن مجموعات من 26 منتجًا مع التكرار ، وبطاقة واحدة حمراء.

في ظل هذه الظروف ، يكون حساب الاحتمال الرياضي للفوز أكثر تعقيدًا إلى حد ما مما اقترحه مؤلف المنشور الأصلي. تتكون اللعبة من عدة طبقات:

• احتمال فتح بطاقات N بدون فتح البطاقة الحمراء هو احتمال مدة مختلفة للعبة ، بغض النظر عما إذا كانت ستكون هناك جائزة.
• احتمالية تجميع مجموعة من 3 بطاقات بنفس السلع. يختلف هذا الاحتمال باختلاف مدة اللعبة. من المهم أن نفهم أن مجموعة من 8 بطاقات تحتوي على سلع ودائما واحدة حمراء لا تحتوي بالضرورة على زوج واحد على الأقل من البطاقات المتطابقة ، ناهيك عن ثلاث بطاقات في آن واحد.

لنبدأ بواحدة بسيطة - فهم كيف سينخفض ​​عدد المشاركين مع زيادة عدد البطاقات التي يفتحونها بسبب قاعدة البطاقة الحمراء.

احتمالات أطوال مختلفة للعبة

نحن نحسب مدى احتمالية فتح الأحمر للمحاكمات N (البطاقات المفتوحة).

UPD: في البداية ، حسبنا احتمالية فتح اللون الأحمر باستخدام توزيع ذي حدين. لم يضمن لنا ذلك بطاقة حمراء واحدة بدقة ، مع هذا التوزيع كان هناك على الأرجح بطاقة حمراء واحدة ، ولكن يمكن أن يكون هناك إما 0 أو 9 مع احتمال ضئيل جدًا. مرة أخرى ، بفضل Stecenko لإشارته إلى خطأ في التعليق واقتراح الحل الصحيح .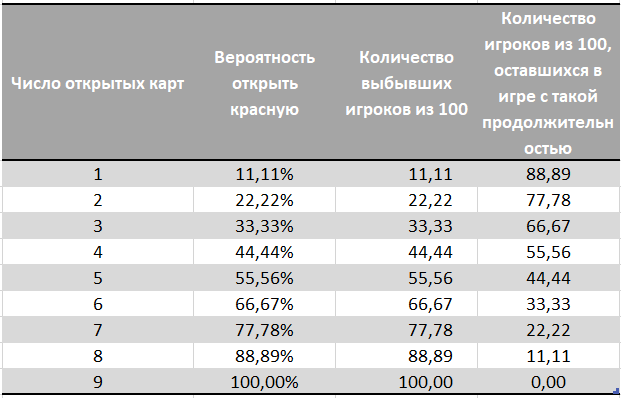



يوضح العمود الأخير عدد اللاعبين من أصل مائة المتبقين في اللعبة مع هذه المدة. يتم استبعاد بقية اللاعبين بسبب البطاقة الحمراء ، دون معرفة ما إذا كان هناك تركيبة فائزة في مجموعة البطاقات الصادرة.

الآن سنحسب احتمالات جمع مجموعة من ثلاث بطاقات بنفس السلع. هذا شرط لاستلام الجائزة.

فرص الجائزة

نحن نحلل اللعبة منطقيا. نفتح البطاقة الأولى ، ثم نختار الزوج لهذه البطاقة ، ونختار الثلاثة للزوج. باستخدام هذا النهج ، يمكننا حساب احتمالية الحصول على 3 بطاقات متطابقة في ثلاث محاولات أو أكثر ، استنادًا إلى حقيقة وجود 26 منتجًا في اللعبة.

بالنسبة للمهام التي تحتوي على عدد ثابت من الاختبارات أو الاختبارات ، إذا كانت نتيجة أي اختبار يمكن أن تكون فقط نجاحًا أو فشلًا ، تكون الاختبارات مستقلة ، ويظل احتمال النجاح ثابتًا طوال التجربة ، سنستخدم صيغة برنولي - في Excel ، وظيفة BINOM.DIS.

باستخدام دالة BINOM.RASP ، يمكنك حساب ، على سبيل المثال ، احتمال أن يكون اثنان من المواليد الثلاثة التاليين من الأولاد. ما هي احتمالية اكتشاف ثلاث منها في ثلاث محاولات؟

= BINOM.RASP (3؛ 3؛ 1/26؛ 0) بالقناع
= BINOM.DISP (عدد النجاحات ؛ عدد التجارب ؛ احتمال النجاح ؛ لا يتجزأ)

أو هنا صيغة حساب احتمال الحصول على 3 سلع متطابقة ومحددة في 8 محاولات.

= BINOM.RASP (3 ؛ 8 ؛ 1/26 ؛ 0) ، أليس كذلك؟

ليس بالفعل. عندما وصلنا إلى مدة المباراة في 4 تجارب ، وعدم السماح بفتح اللون الأحمر ومواصلة اللعب ، حصلنا على موقف مع إمكانية وجود زوجين لاختيار ثلاثة فائزين.

تقليديا ، سلعتان من أصل 26 هما A و B. بطاقاتنا المفتوحة هي A-B-A-B. لم يعد الاحتمال 1/26 ، ولكن 1/26 + (1/26) * "احتمالية زوجين لمدة معينة من اللعبة . "

احتمال اثنين من أزواج لمدة معينة من اللعبة = BINOM.DISP (2؛ 5؛ 1/26؛ 0) ^ 2

عند الوصول إلى لعبة أطول في المحاولة السابعة ، نحصل على تركيبات مثل A-B-A-B-B-B. هذا يعني أن الاحتمال متساوٍ الآن

= 1/26 * (1 + BINOM.RASP (2؛ 7؛ 1/26؛ 0) ^ 2 + BINOM.RASP (2؛ 7؛ 1/26؛ 0) ^ 3) ونحن نبحث عن بطاقة ثالثة لـ 1 ، 2 أو ثلاثة أزواج.

UPD: أيضًا ، في البداية لم نأخذ في الاعتبار أن المحاولة الأولى في حسابنا للمكاسب ، التي تم مسحها من احتمال اختيار المنتج الأحمر ، هي اكتشاف أي من المنتجات الـ 26 ، مما يعني نجاحًا بنسبة 100٪. عدد التكرارات لمنتج في المصفوفة هو عدد التطابقات مع أي منتج واحد ، مما يعني أن تكرارين لمنتج واحد يكفي للفوز ، ولا يتطابقان 3 مع نتيجة محددة متوقعة. وبالتالي ، فإن الاختيار الأول لأي بطاقة ومحاولتين لالتقاط اثنتين إضافيتين من نفس النموذج ما مجموعه ثلاث تجارب.

بمعرفة الاحتمالات ، نحن نبني مصفوفة:



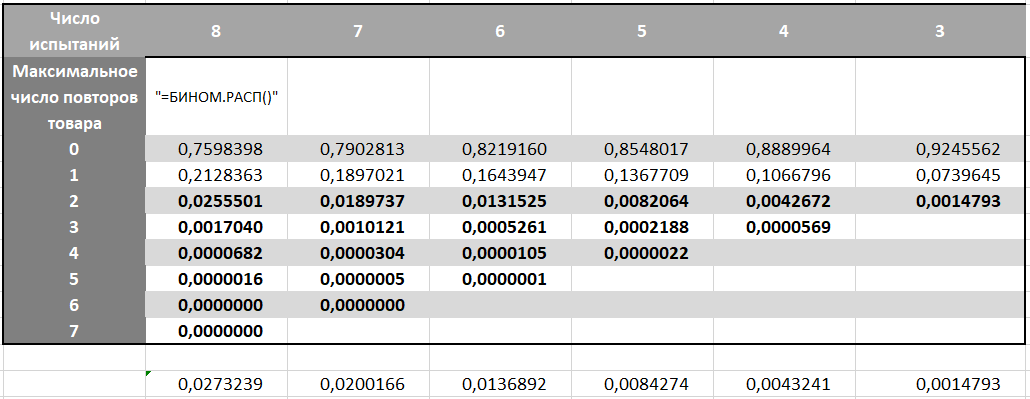
نجد فيه احتمال كل عدد أقصى من التكرارات لمنتج لكل متغير من مدة اللعبة. تذكر أن احتمال ربح التغييرات في المحاولة الرابعة وفي 7 ، مما يعني أننا نأخذ هذا في الاعتبار في صيغة BINOM.RASP

نحن بحاجة إلى خيارات بحد أقصى لعدد التكرار لأي منتج يبلغ 3 أو أكثر. نظرًا لأن اللعبة ستتوقف بمجرد أن نجمع الثلاثة ، فإننا نضيف الاحتمالات حسب الأعمدة في المنطقة بالخط العريض.



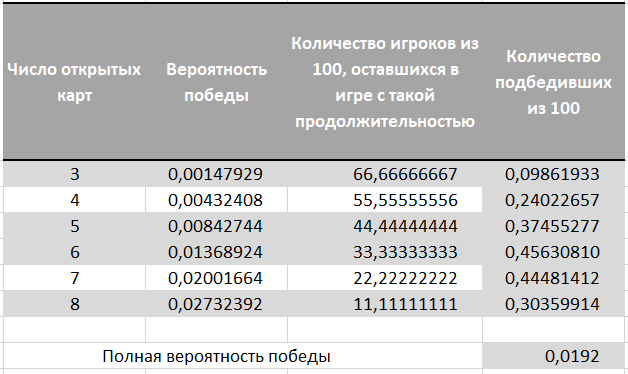
بعد ذلك ، نقوم بمضاعفة فرص مدة كل مباراة في فرص الفوز بجائزة بهذه المدة. تلخيص هذه القطع ، نحصل على احتمال 0.0192 أو 192 فائزًا لكل 10000 لاعب.

نعم ، إنه في الواقع احتمال ضعيف للغاية. على الإطلاق 25٪. دعونا نلقي نظرة على قواعد اللعبة مرة أخرى:

8. صندوق الجائزة:

8.1. الجوائز المتاحة: الأسماء والكميات
...
المجموع 166000

نقسم 116000 على احتمال الفوز ونحصل على حوالي 6 ملايين مشارك من أجل لعب جميع الجوائز. تذكر أنه في 1 يناير 2018 ، وفقًا لـ Rosstat ، كان هناك 146 938921 مقيمًا دائمًا في روسيا. على ما يبدو ، هذه هي فكرة منظمي اللعبة - لإعطاء فرصة للفوز بكل مواطن روسي تقريبًا.

UPD: تغير الاحتمال النهائي بعد التغييرات. يمكننا الآن اختبار حساباتنا في الممارسة العملية بمساعدة النصوص ، لكن موهبة الله العقلية للرياضيين والمنظرين للأجيال السابقة مذهلة ، الذين حسبوا هذا العدد من الاحتمالات ، وإيجاد الحل الصحيح على الورق واستخدام التجارب العقلية.

أظهر تحليل الكود مؤلف المنشور الأصلي أنه حتى قبل بداية اللعبة ، فإن البرنامج النصي "يعرف" نتائجه ، ولكن لا أحد يعرف ما هي النتيجة المحددة سلفًا التي سيعطيها البرنامج النصي لمستخدم معين. بمعرفة الجانب الرياضي للقضية ، ستتمكن أنت بنفسك من الاستنتاج بشأن صدق المنظمين.