منطق غامض للتحكم
النص مبني على مواد من كتاب جوستيف. "المنظمون الغامضون في أنظمة النمذجة الآلية." مثل جميع المنشورات الجادة حول الموضوع ، هذا الكتاب مكتظ بالحسابات الرياضية ويصعب على القارئ غير المستعد. وفي الوقت نفسه ، فإن مبادئ إنشاء واستخدام المنطق الضبابي في حد ذاتها بسيطة وواضحة. هذا النص هو محاولة لترجمة مثال من كتاب من لغة رياضية إلى لغة هندسية.
يتم عرض تسلسل محتمل لتصميم وحدة تحكم بناءً على منطق غامض من خلال تعقيد القواعد المنطقية بالتسلسل واختيار المعلمات باستخدام طرق التحسين.
بيان المشكلة
النظر في توليف وحدة تحكم PID الرقمية وجهاز تحكم غامض لنظام التحكم الصاروخي من زاوية الهجوم. باستخدام النمذجة الرياضية ، نحدد العمليات في النظام ونقدم تقييمًا مقارنًا لجودة النظام باستخدام وحدات التحكم المركبة.
أخذ زاوية الهجوم عند تنسيق خروج الصاروخ:  ولإدخال تنسيق زاوية التوجيه
ولإدخال تنسيق زاوية التوجيه  تحديد وظيفة نقل الصاروخ في الشكل:
تحديد وظيفة نقل الصاروخ في الشكل:
 حيث:
حيث:
 - معامل تحويل الصواريخ ،
- معامل تحويل الصواريخ ،
 - معامل التخميد ،
- معامل التخميد ،
 - ثابت الزمن.
- ثابت الزمن.
فيما يلي ، لا يتم استخدام "دالة التحويل" في تعريف كلاسيكي صارم ، كنسبة من تحويلات لابلاس.
في دراسة نظام التحكم ، افترض أنه تم تحديد اعتماد معلمات الصاروخ على وقت الرحلة على النحو التالي:

لتبسيط الحسابات ، نصف آلية التوجيه من خلال وظيفة التحويل لرابط الدمج  في هذه الحالة ، إدخال النظام
في هذه الحالة ، إدخال النظام  - نظرا لزاوية الهجوم ، خرج النظام
- نظرا لزاوية الهجوم ، خرج النظام  هل زاوية الهجوم التي صنعها الصاروخ ، m (t) هي إشارة التحكم عند خرج وحدة التحكم ، ويتم وصف كائن التحكم بواسطة وظيفة النقل العامة:
هل زاوية الهجوم التي صنعها الصاروخ ، m (t) هي إشارة التحكم عند خرج وحدة التحكم ، ويتم وصف كائن التحكم بواسطة وظيفة النقل العامة:

(يتم تضمين معدات التوجيه التناظرية والصواريخ في عنصر التحكم).
يعطى قانون الاختلاف في عمل المدخلات كثير الحدود:

من الضروري تطوير جهاز تحكم يضمن تطوير تأثير الإدخال باستخدام جهاز تحكم PID وجهاز تحكم يعتمد على المنطق الضبابي.
لاختيار معاملات المنظمين.
مقارنة عابر مع وحدة تحكم PID وجهاز تحكم استناداً إلى منطق غامض.
نموذج كائن ديناميكي
إنشاء نموذج ديناميكي في بيئة النمذجة الهيكلية.
يظهر نموذج الدائرة نفسها في الشكل 1.
يتم تعيين الإجراء المحدد في شكل كتلة ثابتة ، يتم تعيين متغير من البرنامج النصي كمعلمات. يتم تعيين معلمات دالة الانتقال في شكل متغيرات.
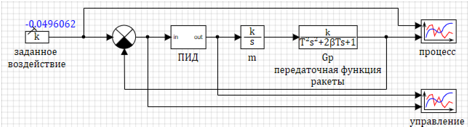 الشكل 1. رسم تخطيطي لنموذج ديناميكي للصاروخ.
الشكل 1. رسم تخطيطي لنموذج ديناميكي للصاروخ.إعداد المنظم
وكتلة PID عبارة عن نموذج فرعي (الشكل 2) يستخدم الكتلة القياسية "جهاز التحكم PID المنفصل". يتم تحديد معدل أخذ العينات يساوي 0.001 ثانية.
 الشكل 2 الشكل 2. تحكم PID مع دارة ضبط.
الشكل 2 الشكل 2. تحكم PID مع دارة ضبط.يتم تعيين معلمات وحدة التحكم في شكل أسماء إشارات عالمية للمشروع
Kp ، Ki ، Kd. هذا يسمح لك بتغيير المعلمات أثناء المحاكاة ، وضبط المنظم.
تم استخدام كتلة
"التحسين" لضبط المنظم ، ومعيار التحسين هو الحد الأدنى للانحراف المعياري.
تقوم وحدة التحسين بإجراء التحسين طوال عملية الانتقال. نتيجة التحسين هي متجه لثلاثة معاملات ، يتم إرسالها إلى كتلة "الكتابة إلى قائمة الإشارات" ، حيث يتم نقل القيم المحسوبة إلى الإشارات ، وبالتالي تتغير قيم معاملات PID. لتكوين وحدة التحكم ، نقوم بتعيين معلمات التحسين التالية:
القيم الأولية لجميع المعاملات
1.يتم تعيين نطاق للاختيار من
-50 إلى
+50دقة الاختيار
0.001أقصى انحراف معياري بعد التحسين
0.01في هذه الحالة ، قامت وحدة التحسين بحساب القيم المثالية التالية للمعاملات:
Kp = -1.7498597 ؛ Ki = 17.891995 ؛ دينار كويتي = 11.606602 .
مع هذه المعاملات ، كان الانحراف المعياري في عابر معين
0.008738090
الشكل 3. عابر.
| 
الشكل 4. الإدارة. |
تحكم المنطق الضبابي
المزايا الرئيسية لجهاز التحكم القائم على المنطق الضبابي هي بساطة ووضوح تشكيل قواعد التحكم في الكائن.
على سبيل المثال ، في كتاب "المنظمون المشوشون في أنظمة النمذجة التلقائية" ، يتم وصف قواعد التنظيم المشوشة للتحكم في الصاروخ بزاوية الهجوم في شكل تعبير رياضي:

أين

- أخطاء النظام وأخطاء تغيير السرعة (المشتقة الأولى) وأخطاء التسارع (المشتقة الثانية) ؛
م - إجراء التحكم على الكائن ؛

- التقديرات اللغوية للخطأ ، ومعدل تغير الخطأ (المشتق الأول) للخطأ والمشتق الثاني للخطأ ، وتعتبر مجموعات ضبابية محددة على مجموعة عالمية

؛

- التقديرات اللغوية لإجراء التحكم على الكائن ، مختارة من مجموعات المصطلحات من متغير
مقد يتساءل القارئ: كيف حال والدتك ، أنا آسف ، مفهوم؟
في بعض الأحيان تشكك زحف في أن يفهم علماء الرياضيات أنفسهم ما كتبوه. وراء المنعطفات الرياضية الصعبة ، يخفي السر العظيم لقواعد التنظيم الغامض. ها هي:
تقلل كثيرا
القاعدة - لا تلمس
زيادة صغيرةإذا كنت تترجم من لغة الرياضيات للطيور إلى الروسية ، ثم التعبير

تعني حرفيا ما يلي:
إذا كان
أكثر من المعتاد وزاد الانحراف وزاد معدل النمو ، فإننا
ننخفض .
إذا
لم يتغير المعيار وكانت
السرعة ثابتة ،
فلن نغير .
إذا كانت
أقل من المعتاد وهبطت وتزداد نسبة الهبوط ، ثم
تزداد .
إذا كنت تفهم ما هو مخفي حقًا وراء الضباب الرياضي ، فيمكنك الاقتراب من إنشاء المنظمين بوعي أكبر والحصول على نتائج أكثر إثارة للاهتمام.
جزء من النظرية
لحل مشكلة ضبط زاوية الهجوم ، يجب أن نحصل على ثلاثة مصطلحات من قيمة الانحراف المستمر - أقل ، عادي ، أكثر. يجب أن يتم نفس الشيء بالنسبة للمشتق الأول للانحراف والمشتق الثاني للانحراف. هذه هي المرحلة الأولى من الاستدلال الضبابي - مراحل.
للحصول على المصطلحات ، نحتاج إلى تعيين القيمة العددية للمعلمة لكل مصطلح. على سبيل المثال: "Little" = -1؛ "نورم" = 0 ؛ "كثير" = 1. للتدريج سنستخدم الدوال الثلاثية. تنمو الوظائف كلما اقتربت من القيمة المحددة ، وتنخفض كلما ابتعدت. يظهر خياران للوظائف الثلاثية في الشكل 5:

 الشكل 5. وظائف العضوية الثلاثي.
الشكل 5. وظائف العضوية الثلاثي.من خلال معرفة الانحراف (x1) ، يمكننا العثور على قيم دالة العضوية للمصطلحات أكثر (الخط الأحمر) ، القاعدة (الخط الأخضر) ، أقل (الخط الأزرق). تتراوح القيم من 0 إلى 1.
يرجى ملاحظة أن الوظائف المتطرفة على المخطط الأيسر ليست "ثلاثية" تمامًا. إذا اعتبرنا ذلك من وجهة نظر الرياضيات المجردة ، فإن الوظائف على الرسم البياني الأيمن تكون أكثر "جمالًا". ولكن ، إذا كنت تتذكر "السر الرئيسي لقواعد الاستدلال الغامض" ، فإن المخطط الأيسر أكثر صحة. في الحقيقة:
ضع في اعتبارك القاعدة
"إضافة - صغيرة" ، إذا كانت لدينا قيمة -1 ، فإن
"القليل" = 1 (الخط الأحمر) صحيح لكل من الرسم البياني. وإذا كان لدينا قيمة -2؟ منطقيا ، يجب أن
نضيف أيضا. على الرسم البياني الأيسر عند -2 هو:
"little = 1" ، ولكن على الرسم البياني الأيمن لدينا
"little" = 0 ، وهو أمر غير صحيح بشكل واضح. وينطبق الشيء نفسه على قاعدة
"تقليل الكثير" .
يمكن أن يؤدي الترحيل بالوظائف الثلاثية "الصادقة" إلى حقيقة أنه عندما تتجاوز القيمة نطاق تعريف الوظائف ، نحصل على 0 لجميع المصطلحات ، والتي بدورها يمكن أن تؤدي إلى عدم وجود تأثير على الكائن.
المشكلة العكسية هي التشديد. لحساب التأثير ، تحتاج إلى إجراء التحويل العكسي - لدينا قيم وظائف العضوية لتقليل النطاق (
0 ... 1 ) (التوابع الثلاثية) ونطاق التأثيرات التي يمكننا الحصول عليها ، وليس تغييرها ، ويجب أن نحصل على أحد المصطلحات الثلاثة الرقم له تأثير محدد.
يمكنك الحصول على التأثير بطرق مختلفة ، على سبيل المثال ، في وسط كتلة الشكل. يوضح الشكل 6 حالة وحدة التحكم ، حيث تنخفض قيم المصطلحات
0.3 ولا تغير
0.6 وتزيد
0.8 مع نطاق التأثير التنظيمي
-30..30 التأثير الناتج =
4.1.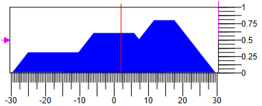 الرقم 6 الشكل. تشويه إجراءات المراقبة
الرقم 6 الشكل. تشويه إجراءات المراقبةخيار آخر للتشويه هو في مركز كتلة النقاط. يوضح الشكل 7 خيارًا ، حيث نحصل على إجابة أخرى
8.82 لنفس قيم المصطلحات ونطاق التحكم:
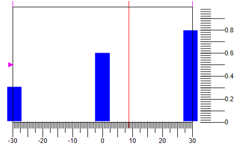 الرقم 7 الشكل. تشويه مركز كتلة النقاط.
الرقم 7 الشكل. تشويه مركز كتلة النقاط.يجب أن يُفهم أنه بالإضافة إلى طريقة الاستدلال ، يؤثر شكل وظيفة العضوية أيضًا على النتيجة. على سبيل المثال ، يمكنك اختيار هذه الدوال المثلثية التي تكون قاعدة المثلث هي نفسها ، تختلف القمم فقط. (انظر الشكل 8).
 الشكل 8. وظائف العضوية الثلاثية مع قاعدة واحدة.
الشكل 8. وظائف العضوية الثلاثية مع قاعدة واحدة.في هذه الحالة ، لتقليل نتيجة الإنهاء عند نفس قيم المصطلحات 0.3 ، لا تغير 0.6 وتزيد -0.8 مع نطاق التأثير التنظيمي -30 ، 30 التأثير الناتج =
5.27 .
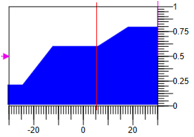 الشكل 9. إزالة التشويه حسب حساب المنطقة.
الشكل 9. إزالة التشويه حسب حساب المنطقة.مسلحين بالمعرفة السرية للمنطق الضبابي ، سنقوم بإنشاء نموذج تحكم. نترك نموذج الصاروخ كما هو بالنسبة لوحدة التحكم PID (انظر الشكل 1) ، ولكن في النموذج الفرعي لوحدة التحكم ، نقوم بتجميع الدائرة الموضحة في الشكل 10.
 الشكل 10. دائرة التحكم على أساس المنطق الضبابي.
الشكل 10. دائرة التحكم على أساس المنطق الضبابي.عند مدخل المنظم ، يتم تطبيق عدم تطابق بين زاوية الهجوم المحددة والواقعية (المقاسة). بعد الإدخال توجد كتلة "Extrapolator" ، والتي توفر تحويل إشارة مستمرة إلى إشارة منفصلة مع فترة أخذ عينات معينة (0.001 ثانية هي نفس وحدة تحكم PID منفصلة).
بعد ذلك ، يتم حساب الانحرافات الأولى والثانية. للقيام بذلك ، نحسب الفرق بين القيمة الحالية والقيمة مع تأخير لفترة التكمية ، ونقسمها على وقت التأخير (المعامل في كتلة المقارنة). وبالتالي ، نحصل على ثلاثة مدخلات: خطأ في النظام ، معدل التغيير (المشتق الأول) للخطأ ، التسارع (المشتق الثاني) للخطأ.
يتم تحويل قيمة متغيرات الإدخال بواسطة كتل التدوير إلى وظائف مثلثة. لكل متغير ، نحصل على ثلاثة متغيرات لغوية (تسعة في المجموع).
يقوم Demultiplexer بحجب المتجهات إلى متغيرات لغوية لتكوين القواعد. في الرسم البياني ، يتم توقيع أسماء المتغيرات بترتيب ترتيبها في المتجهات.
الانحراف في حالتنا هو الفرق بين المجموعة والقياس ، إذا كانت القيمة السالبة تعني أن زاوية الهجوم أكبر من المجموعة ، يجب علينا تقليلها. وبالتالي ، على العكس من ذلك ، إذا كان الانحراف موجبًا ، فإن الزاوية المقاسة أقل من الزاوية المحددة ، يجب أن نزيدها.
(المزيد - تقليل ، أقل - زيادة ، القاعدة - لا تلمس) .
يحتوي الناتج أيضًا على ثلاثة متغيرات لغوية "تقليل" ، "لا تتغير" ، "زيادة". يقوم معدد الإرسال بجمع القيم في متجه وإرساله إلى كتلة الإخراج المشوشة. الآن بعد أن أصبح لدينا جميع المتغيرات ، يمكننا كتابة قواعد الاستدلال الغامض في شكل رسم بياني.
- إذا كان أكثر من المعتاد وزاد الانحراف وزاد معدل النمو => النقصان.
- إذا كان المعيار لا يتغير وكان ثابتًا => فلن نغير.
- إذا كانت أقل من المعتاد وهبطت وزاد معدل السقوط => الزيادة.
ترتبط جميع المتغيرات اللغوية في القواعد من خلال الكتل المنطقية "و" وترتبط بالنواتج. كما يتبين من الشكل 10 ، لا تختلف دائرة الاستدلال الضبابي المنطقي عمليا عن الدائرة المنطقية المعتادة ، بل يتم استخدام الكتل المنطقية الضبابية فقط.
على غرار ضبط وحدة تحكم PID ، نستخدم كتلة التحسين.
يبقى السؤال مع معلمات الكتل.
توليف وحدة تحكم على أساس منطق غامض
لا يوجد شيء في الحياة مقابل لا شيء ، وبالتالي ، يتم تعويض بساطة قواعد التنظيم من خلال عدد المعلمات التي تصف وظائف العضوية. في الواقع ، إذا كنت بحاجة إلى تحديد ثلاثة معاملات لوحدة تحكم PID ، في حالة المنطق الضبابي ، تحتاج وظيفة مثلثية واحدة فقط إلى 3 أرقام للرؤوس. إذا احتاجنا لكل متغير إدخال 3 وظائف عضوية + 3 للإخراج ، اتضح أننا بحاجة إلى تعيين 3 × 3 × 3 + 3 × 3 = 36 معلمة!
ولكن ليس كل شيء محزن للغاية. من أجل التقريب الأول والإعداد الأولي ، يمكن تبسيط كل شيء.
بعد إجراء بعض الافتراضات للتعديل الأولي لوحدة التحكم:
- قمنا بتعيين تناظر الدالات فيما يتعلق بالصفر ، ثم بدلاً من رقمين للحد الأقصى والحد الأدنى ، يمكنك تحديد واحد - الحد الأقصى ، وبالتالي ، سيتم تعريفه على أنه نطاق [ -Max ... Max ].
- نقوم بتعيين توزيع موحد للوظائف ، ثم يمكننا حساب موضع جميع رؤوس المثلثات بناءً على نطاق معين.
- لثلاث وظائف ، يتم تعريف إحداثيات القمم على أنها -Max ، 0 ، Max.
- نضع أن قاعدة المثلث لجميع وظائف العضوية هي نفسها.
وبالتالي ، بدلاً من 36 معلمة مستقلة ، يجب تحديد 4 فقط ، والانحراف الأقصى من 0 لثلاثة متغيرات إدخال ومخرج واحد ، وهي:
uMax - اتساع إجراء التحكم
(-uMax ... uMax) ؛
deltaMax - أقصى انحراف
(-deltaMax ... deltaMax) ؛
divMax - مشتق أقصى للانحراف
(-divMax ... divMax) ؛
div2Max - المشتق الثاني الأقصى للانحراف
(-div2Max ... div2Max)في وظائف الاستدلال والاستدلال الضبابي ، نستخدم هذه الإشارات لحساب المعلمات مع مراعاة الافتراضات المقبولة.
إعدادات وحدة التحكم المقترحة في الكتاب بواسطة VV Gostev "المنظمون المشوشون في أنظمة النمذجة الآلية" ، في حالة التصفية التدريجية بواسطة ثلاث وظائف عضوية ، تُقترح المعلمات التالية:
uMax = 30 - سعة عمل التحكم ؛
deltaMax = 0.01 - أقصى انحراف ؛
divMax = 0.07 - أقصى مشتق للانحراف ؛
div2Max = 1 هي المشتق الثاني الأقصى للانحراف.
مقارنة عابرة
على الرسم البياني العابر ، تكاد تكون مصادفة تأثير معين والنتيجة التي تم الحصول عليها مكتملة:

الشكل 11.أ عابر. تحكم PID
| 
الشكل 11.ب. عابر. منطق غامض
|
يمكن رؤية الاختلافات الواضحة على الرسوم البيانية للانحراف والتحكم الناتج:

الشكل 12.أ. الإدارة. تحكم PID
| 
الشكل 12.ب. الإدارة. منطق غامض |
من مقارنة الأرقام ، يُلاحظ أن وحدة التحكم المشوشة توفر خطأ أقل ، وعابرة أفضل.
دعونا نقارن العابرين في النظام إذا قمنا بتعيين إجراء تحكم تدريجي. النتائج في الشكل 13:

الشكل 13.أ. تأثير الخطوة. تحكم PID.
| 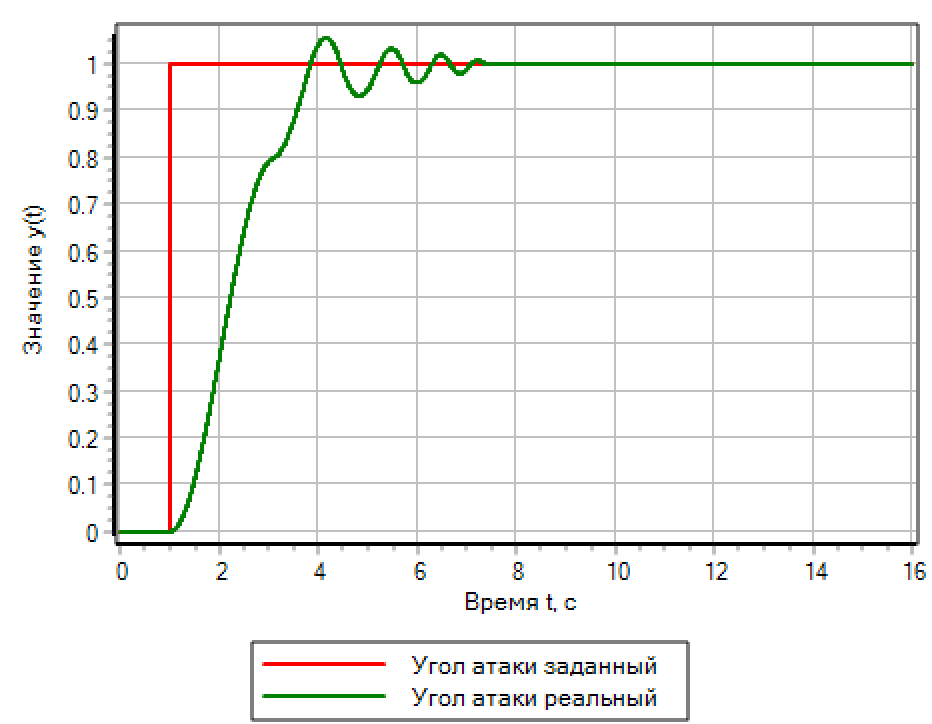
الشكل 13.ب. تأثير الخطوة. منطق غامض. |
للعمل التدريجي ، توفر وحدة التحكم القائمة على المنطق الغامض أفضل جودة عابرة. وحدة التحكم PID ، التي يتم ضبطها تلقائيًا على عملية سلسة ، تتسبب في حدوث تذبذبات مع تجاوز السرعة هي ضعف الخطوة المحددة.
تعديل وحدة التحكم على أساس المنطق الضبابي من خلال طريقة التحسين
دعنا نحاول تحديد معلمات وحدة التحكم المشوشة بطريقة التحسين ، تمامًا كما حددناها لوحدة تحكم PID. كمعيار ، قمنا بتعيين الانحراف المعياري أقل من 0.001.
تجدر الإشارة إلى أن هذه الطريقة ليست صحيحة تمامًا ، لأنه بالنسبة للمحترفين ، من الواضح أي الزوايا والسرعات هي الحد الأقصى والحد الأدنى لكل قطعة موسيقية ، مما يسمح لك بتعيين قيود على المعلمات المحسنة بشكل أكثر وعيًا ، نقوم بتعيين المعلمات الافتراضية ونرى ما سيحدث.
قامت طريقة التحسين بالإعدادات الافتراضية بحساب القيم التالية لنطاقات معلمات التحسين:
uMax = 19.377 - اتساع عمل التحكم ؛
deltaMax = 1.095 - أقصى انحراف ؛
divMax = 0.01 - أقصى مشتق للانحراف ؛
div2Max = 2.497 هي المشتق الثاني الأقصى للانحراف.
في حالة التحسين البسيط للانحراف ، توفر المعلمات التي تم الحصول عليها الدقة المحددة ، ومع ذلك ، فإن هذا يسبب تذبذبات عالية التردد لإجراء التحكم.
يتم عرض وظيفة الانتقال وإجراءات التحكم في الشكل 14.أ
 الشكل 14.أ. منطق غامض. إعداد الانحراف. الشكل 14.أ. منطق غامض. إعداد الانحراف.
| 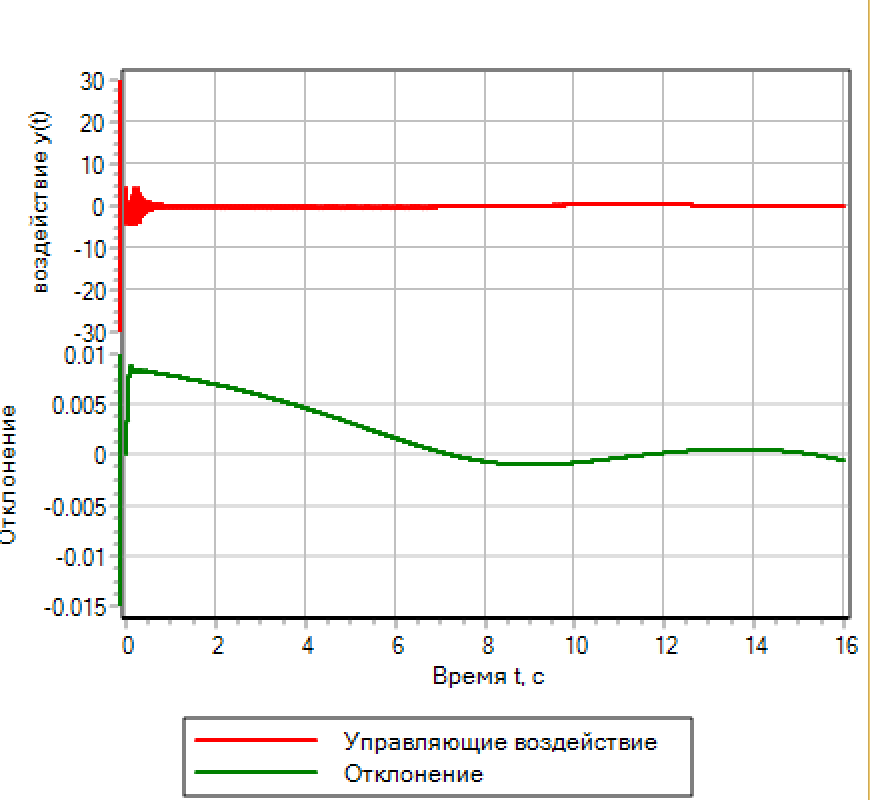 الشكل 14.ب. منطق غامض. الإعداد بالانحراف وعدد الردود. الشكل 14.ب. منطق غامض. الإعداد بالانحراف وعدد الردود. |
من أجل تحسين العملية العابرة ، يمكن للمرء أن يضيف إلى معيار التحسين عدد تحويلات المنظم من القيمة السلبية إلى القيمة الإيجابية لتأثير التنظيم (المخطط في الشكل 15).
 الشكل 15. مخطط للتحسين حسب معيارين.
الشكل 15. مخطط للتحسين حسب معيارين.يعطي الحساب بطريقة التحسين وفقًا لمعيارين قيم المعلمات التالية:
uMax = 19.714 - اتساع عمل التحكم ؛
deltaMax = 1.0496 - أقصى انحراف ؛
divMax = 0.01 - أقصى مشتق للانحراف ؛
div2Max = 1.7931 هي المشتق الثاني الأقصى للانحراف.
يمكن ملاحظة أنه عندما تمت إضافة عدد الرحلات إلى معيار التحسين ، كان من الممكن تقليل تردد التحويل للمنظم (انظر الشكل 14. ب). وبالتالي ، يمكننا القول أن طريقة التحسين تعمل حتى عندما لا نعرف شيئًا عن فيزياء الكائن ونختار ببساطة المعلمات العددية دون التفكير في معناها الجسدي.
إنشاء وحدة تحكم خاصة بك على أساس منطق غامض
أعلاه ، أنشأنا وحدة التحكم وفقًا لمخطط مُعد بالفعل وبسيط إلى حد ما ، تم توصيل جميع مصطلحات المتغيرات اللغوية بواسطة العامل المنطقي الأول. نظرًا لأن لدينا نفس عدد المصطلحات في المدخلات والمخرجات ، فهذا هو أبسط الحلول وأكثرها وضوحًا.
دعنا نحاول إنشاء وحدة تحكم لا تحتوي مخرجاتها على 3 مصطلحات ، ولكن ، على سبيل المثال ، 5:
تقليل سريعًا ، تقليل ، عدم تغيير ، زيادة ، زيادة سريعة . وعند المدخل نفسه.
دعنا نغير منطق المنظم ، بالنسبة للمبتدئين ، لتبسيط خوارزمية التحكم قدر الإمكان.نكتب القواعد:1) إذا كان يعد و Raste ص => ينخفض بسرعة.2) إذا كان المزيد => النقصان.3) إذا كانت القاعدة => لا تتغير.4) إذا كانت أقل => زيادة.5) إذا كان أقل و يكون menshaetsya => زيادة بسرعة.في هذه الحالة ، لدينا 5 مصطلحات (5 وظائف مثلثة) لمتغير الإخراج. نحن نقبل أن يتم توزيعها بالتساوي بين -uMax و + uMax.نفترض أن الدوال الثلاثية تتكون بطريقة تجعل دالات العضوية في المصطلح تأخذ قيمًا قصوى ، تأخذ الدوال المجاورة قيمًا صفرية (انظر الشكل 5).كمعلمات للناتج ، سيتم استخدام الانحراف ومعدل التغيير فقط.لتسريع الحسابات ، نستخدم مراحل إخراج الطريقة بواسطة مركز ثقل النقاط (انظر الشكل 7).ستبدو دائرة التحكم في هذه الحالة كما هو موضح في الشكل 15.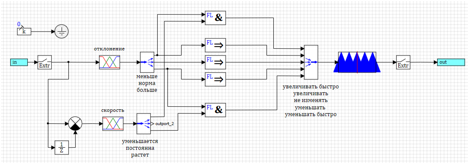 الشكل 15. وحدة تحكم مبسطة تستند إلى منطق غامض.بدلاً من نطاق المشتق الثاني للمحسن ، سيتم أخذ قيمة مصطلح "زيادة". تُظهر محاولة ضبط مثل هذا المنظم من خلال طريقة التحسين أنه تم ضبط المنظم ، ولكن جودة تنظيم التحكم في النظام تترك الكثير مما هو مرغوب فيه.يتم عرض أفضل نتيجة في الشكل 16.
الشكل 15. وحدة تحكم مبسطة تستند إلى منطق غامض.بدلاً من نطاق المشتق الثاني للمحسن ، سيتم أخذ قيمة مصطلح "زيادة". تُظهر محاولة ضبط مثل هذا المنظم من خلال طريقة التحسين أنه تم ضبط المنظم ، ولكن جودة تنظيم التحكم في النظام تترك الكثير مما هو مرغوب فيه.يتم عرض أفضل نتيجة في الشكل 16.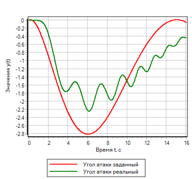 الشكل 16. عابر لوحدة تحكم مبسطة.يمكن ملاحظة أن التنظيم يحدث ، ولكن ليس على الإطلاق كما نود. الحقيقة هي أننا نمارس التأثير عندما يحدث انحراف بالفعل. دعنا نحاول تشغيل التنظيم في الوقت الذي يكون لدينا انحراف في القاعدة ، ولكن السرعة تظهر أنها ستزداد أو تنقص.1) إذا كان أقل و يقلل => زيادة سريعة.2) إذا كان معدل و زادت => مخفضة.3) إذا كانت القاعدة => لا تتغير.4) إذا كان معدل و يقلل => زيادة.5) إذا كان أكبر و ينمو => ينخفض بسرعة.
الشكل 16. عابر لوحدة تحكم مبسطة.يمكن ملاحظة أن التنظيم يحدث ، ولكن ليس على الإطلاق كما نود. الحقيقة هي أننا نمارس التأثير عندما يحدث انحراف بالفعل. دعنا نحاول تشغيل التنظيم في الوقت الذي يكون لدينا انحراف في القاعدة ، ولكن السرعة تظهر أنها ستزداد أو تنقص.1) إذا كان أقل و يقلل => زيادة سريعة.2) إذا كان معدل و زادت => مخفضة.3) إذا كانت القاعدة => لا تتغير.4) إذا كان معدل و يقلل => زيادة.5) إذا كان أكبر و ينمو => ينخفض بسرعة.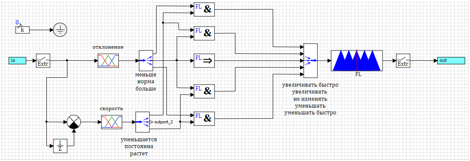 الشكل 17. السيطرة على معدل تغير الانحراف.يتم عرض نتائج تشغيل وحدة التحكم المضبوطة بطريقة التحسين في الشكلين 18 أ و 18 ب.
الشكل 17. السيطرة على معدل تغير الانحراف.يتم عرض نتائج تشغيل وحدة التحكم المضبوطة بطريقة التحسين في الشكلين 18 أ و 18 ب.
الشكل 18.أ. عملية الانتقال.
| 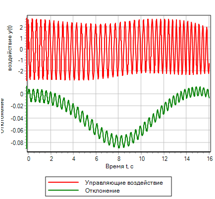
الشكل 18.ب. الإدارة |
تحسن التحكم في معدل تغير الانحراف بشكل كبير العابر. ومع ذلك ، إذا نظرت بعناية إلى مجموعة القواعد المنطقية ، فإننا نرى أن الانحراف غير مشترك في الإدارة. إذا تم إعطاء تأثير الخطوة ، فلن تقوم وحدة تحكم التحكم بإنشاء إجراء تحكم. يوضح الشكل 19 مثالاً لعملية عابرة مع إجراء تحكم تدريجي ، يمكن ملاحظة أن وحدة التحكم لا تعطي إجراء تحكم ، على الرغم من أن الانحراف هو 1.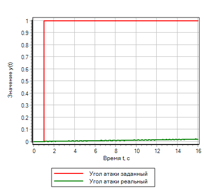
الشكل 19.أ. عملية الانتقال. الخطوة
| 
الشكل 19.ب. الإدارة. الخطوة |
, , . , , . , , :
1)
=> .2) (
)
=> .3)
=> .4) (
)
=> .5)
أكبر و متزايد => ينخفض بسرعة.يتم عرض دائرة التحكم وفقًا لهذه القواعد في الشكل 20.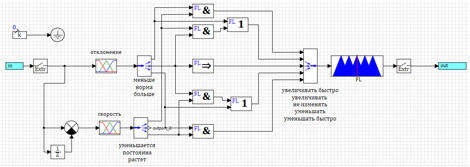 الشكل 20. وحدة تحكم مع التحكم عن طريق الانحراف ومعدل التغيير.نتيجة للتعديل ، لم تتغير جودة عملية الانتقال مع إجراء سلس عمليًا ، ومع ذلك ، مع إجراء تدريجي ، بدأ المنظم في وضع الخطوة وإحضار زاوية هجوم الصاروخ إلى الصاروخ المحدد (انظر الشكل 21).
الشكل 20. وحدة تحكم مع التحكم عن طريق الانحراف ومعدل التغيير.نتيجة للتعديل ، لم تتغير جودة عملية الانتقال مع إجراء سلس عمليًا ، ومع ذلك ، مع إجراء تدريجي ، بدأ المنظم في وضع الخطوة وإحضار زاوية هجوم الصاروخ إلى الصاروخ المحدد (انظر الشكل 21).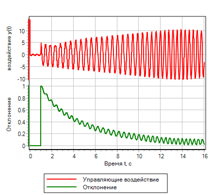
الشكل 21 أ. عملية الانتقال. الخطوة
| 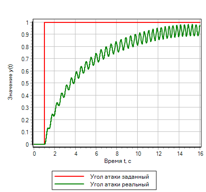
الشكل 21 ب. الإدارة. الخطوة |
, «» .
, , . , , , .
, . , , . , , , :
1)
=> .2) (
)
=> .
3)
=> .4) (
)
=> .5)
=> .
22. «», , , «
& ».
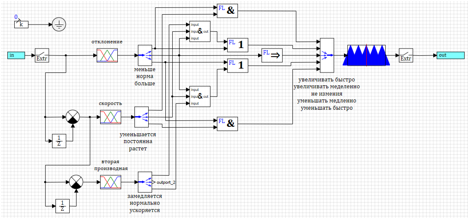 الشكل رقم 22. تحكم المنطق الضبابي مع التحكم في المشتق الثاني.بعد تحديد المعلمات من خلال طريقة التحسين للانحراف وعدد الشوائب ، تم الحصول على المعلمات التالية:uMax = 27.4983 - اتساع إجراء التحكم ؛deltaMax = 0.0433 - أقصى انحراف ؛divMax = 0.0966 - أقصى مشتق للانحراف ؛div2Max = 1.0828 - أقصى مشتق ثان للانحراف.يتم عرض العملية العابرة في الشكل 23. ويمكن ملاحظة أن المنظم الناتج لديه أفضل أداء من جميع تلك المذكورة أعلاه ، ولكن للحصول على تأثير معين. الانحرافات وإجراءات التحكم هي الحد الأدنى من كل ما تم تناوله في هذا النص.
الشكل رقم 22. تحكم المنطق الضبابي مع التحكم في المشتق الثاني.بعد تحديد المعلمات من خلال طريقة التحسين للانحراف وعدد الشوائب ، تم الحصول على المعلمات التالية:uMax = 27.4983 - اتساع إجراء التحكم ؛deltaMax = 0.0433 - أقصى انحراف ؛divMax = 0.0966 - أقصى مشتق للانحراف ؛div2Max = 1.0828 - أقصى مشتق ثان للانحراف.يتم عرض العملية العابرة في الشكل 23. ويمكن ملاحظة أن المنظم الناتج لديه أفضل أداء من جميع تلك المذكورة أعلاه ، ولكن للحصول على تأثير معين. الانحرافات وإجراءات التحكم هي الحد الأدنى من كل ما تم تناوله في هذا النص.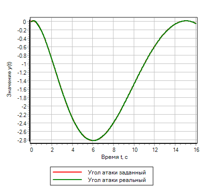
الشكل 23 أ. عملية الانتقال.
| 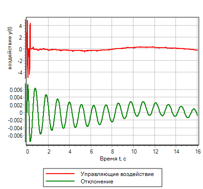
الشكل 23 ب. الإدارة. |
الاستنتاجات
, -.
.
. .
, ,
...