🙎🏿 💶 💫 تحديد الخصائص الباليستية الزمنية لحركة مركز كتلة الهبوط المظلي من طائرة 🌨️ 👌🏽 👸🏻

مقدمة

لتحديد الخصائص الباليستية الزمنية لحركة مركز كتلة المظلي ، يجب على المرء أن يختار نموذجًا رياضيًا مبسطًا يمكن الوصول إليه تمامًا للبحث التحليلي وفي نفس الوقت يحافظ على أكثر السمات المميزة للكائن الأصلي.

لبناء نماذج رياضية مبسطة لحركة المظلي ، يتم إجراء تحليل وتحديد وتنظيم وتنظيم المعلمات الثابتة والزمنية.

لا توجد حاليًا طرق منتظمة ومبررة بشكل كاف لبناء نماذج رياضية غير خطية ، ومع ذلك ، لحل مشاكل معينة ، مع الإعداد الصحيح للأنظمة الأولية للمعادلات التفاضلية غير الخطية ، يمكن أن تعطي الطرق العددية لحلها نتائج كافية تمامًا.

الغرض من هذا المنشور هو تجميع وحل أنظمة المعادلات التفاضلية عدديًا التي تصف جميع مراحل حركة الهبوط المظلي من طائرة ، مع مراعاة تأثير التغيرات في الارتفاع ودرجة حرارة كثافة الكتلة الهوائية.

الخصائص الباليستية الزمنية لحركة المظلي

تشمل المعلمات المتغيرة الثابتة والمحدودة ما يلي:

ح - ارتفاع الافراج عن المظلي.
V0 - سرعة الطائرة ؛
ك - الوزن ، ارتفاع المظلي ؛
g هو تسارع الجاذبية.
ρ هي كثافة الهواء ؛
T هي درجة حرارة الهواء.

تتضمن المعلمات المؤقتة (المتغيرة):

tn - وقت الهبوط ،
w هي سرعة الرياح ؛
V هي سرعة المظلي.
u هي سرعة التدفق الصاعد (الهابط) ؛
د - الانجراف (المسافة من الإسقاط على أرض نقطة الطرد إلى نقطة اللمس) ؛
C هو معامل السحب لجسم الهبوط ؛
و - الجزء الأوسط من جسم الهبوط.

مراحل القفز

المرحلة الأولى هي السقوط الحر بعد الانفصال عن الطائرة:

المرحلة الثانية هي انخفاض مظلة الاستقرار:

الخاصية الرئيسية لمظلة التثبيت هي استقرار المظلي في الوضع الأكثر ملاءمة للمظلة الرئيسية.

المرحلة الثالثة - ملء قبة المظلة الرئيسية:

المرحلة الرابعة هي انخفاض في المظلة المفتوحة:

تجميع نظام المعادلات التفاضلية لجميع مراحل قفزة المظلة

نختار نظام إحداثيات ثابت يتمركزه OXY عند نقطة الإخراج O. يتزامن المحور OX مع اتجاه المكون الأفقي لسرعة الطائرة. يتم توجيه المحور OY عموديًا إلى الأعلى في الاتجاه المعاكس للسرعة الرأسية للمظلي.

سنفترض أن حركة المظلي مسطحة ، وتحدث في طائرة OXY. يمكن اعتبار نموذج القفزة هذا نموذجًا للقفزة في الطقس الهادئ دون مراعاة تأثير الرياح.

نعتقد أنه ، بالإضافة إلى الوزن ، يتأثر المظلي بقوة مقاومة الهواء بما يتناسب مع مربع سرعة المظلي:

،
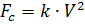
حيث:

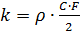
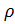
- كثافة الهواء - معامل السحب - F - الجزء الأوسط من الجسم.

مع ارتفاع الارتفاع ، تتغير درجة حرارة الهواء:

وصلت درجة الحرارة الدنيا بالفعل على ارتفاع 10 كم. وهو -55 درجة مئوية. تعتمد كثافة الهواء أيضًا على الضغط. لذلك ، عند حساب المقذوفات لقفزة المظلة ، من المناسب استخدام الصيغة التالية لتحديد كثافة الهواء [1]:

،
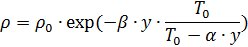
أين

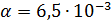
ك / م ؛

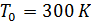
- درجة حرارة سطح البحر ؛ y هو الارتفاع بالمتر ؛

- كثافة الهواء عند y = 0 ؛

قائمة

# -*- coding: utf8 -*- from numpy import* import matplotlib.pyplot as plt beta=1.25*10**-4 alfa=6.5*10**-3 T0=300 y=arange(0,10000,1) x=[exp(-beta*w*T0/(T0-alfa*w)) for w in y] plt.title("  \n    ") plt.plot(x,y) plt.ylabel('  .') plt.xlabel(' ') plt.grid(True) plt.show()

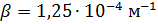
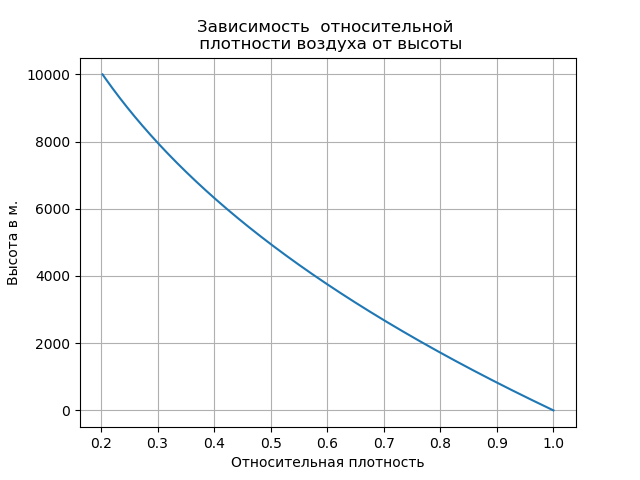
في ممارسة الحسابات ، يؤخذ مربع النمو كوسط. تم العثور على قيمة C من الجدول [2]:

Θ يدل على زاوية ميل المسار. تحت الافتراضات المقدمة للمكونات

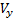
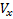
نواقل السرعة V لدينا:

قسمة m على الجانبين الأيسر والأيمن من معادلات النظام الناتج والتعيين

من خلال r نحصل على:

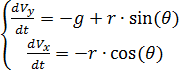
(1)

نكتب معادلات الحركة للقافز المظلي في شكل نظام المعادلات التفاضلية للوظائف V ، θ ، y (t) ، x (t).

بالنظر إلى ما يلي:

،
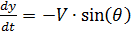
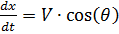
وتمييز النسبة الزمنية:

مع مراعاة نظام المعادلات (1) نحصل على:

.

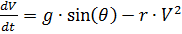
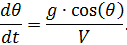
وهكذا ، في ظل الظروف الأولية:

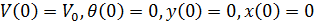
لدينا النظام التالي من المعادلات التفاضلية:

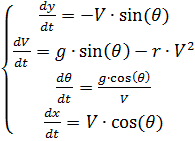
الحل العددي لنظام المعادلات التفاضلية (2) باستخدام بايثون

لحل (2) ، نعيد كتابته بالصيغة التالية ، مع إدخال قوى السحب المستقرة التي يتحكم فيها الوقت وكثافة الهواء

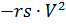
والرئيسية

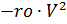
المظلات ، على التوالي ، مضروبة في وظائف التحكم في الوقت ks (t) و ko (t):

،

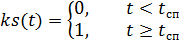
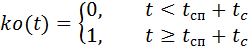
حيث:

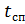
- - وقت السقوط الحر للمظلي.

- وقت تشغيل مظلة التثبيت حتى تفتح المظلة الرئيسية.

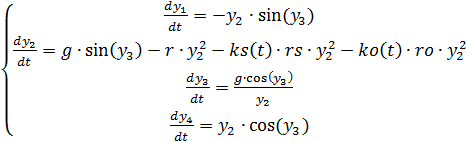
(3)

قائمة كاملة للبرنامج معدلة للتغيرات في كثافة الهواء

 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#   /2 rou0=1.29#  /3 Cp=0.3#    Cpar=0.75#     mp=120#    100+20=120 . s=0.8#   2 ss=1.5#   2 Cpars=0.35#     S=70#   2 tsp=40#    c. tssp=3 #      c. tpr=210#     . h=4000.0#    . V0=100.0#    / beta=1.25*10**-4 alfa=6.5*10**-3 T0=300 def ks(t): if t<= tsp: z=0 else: z=1 return z def ko(t): if t<= tsp+tssp: z=0 else: z=1 return z def f(y,t): y1,y2,y3,y4=y rou=rou0*exp(-beta*y1*T0/(T0-alfa*y1)) rp=0.5*Cp*rou*s/mp rpars=0.5*Cpars*rou*ss/mp rpar=0.5*Cpar*rou*S/mp return [-y2*sin(y3),g*sin(y3)-rp*(y2**2)-ko(t)*rpar*(y2**2)-ks(t)*rpars*(y2**2),g*cos(y3)/y2,y2*cos(y3)] t=arange(0,tpr,1) y0=[h,100,0,0] [y1,y2,y3,y4]=odeint(f, y0,t, full_output=False).T plt.figure() plt.title('     : %s .. \n   : %s /. \n   : %s /'%(h,V0,round(y2[tpr-tsp-tssp],0))) plt.plot(y1,y2*sin(y3),label='  .: %s c. \n     : %s . \n     : %s . '%(tsp,tssp,tpr-tsp-tssp)) plt.xlabel('  .') plt.ylabel('   /') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title("-         \n   ") plt.plot(y1,y4) plt.xlabel('  .') plt.ylabel('     .') plt.grid(True) plt.figure() plt.title("     ") plt.plot(t,y2*sin(y3)) plt.xlabel('  .') plt.ylabel('   /.') plt.grid(True) plt.show()

نحصل على:

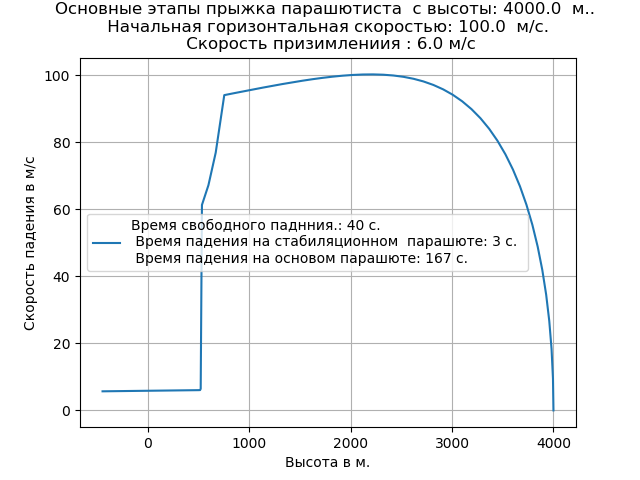
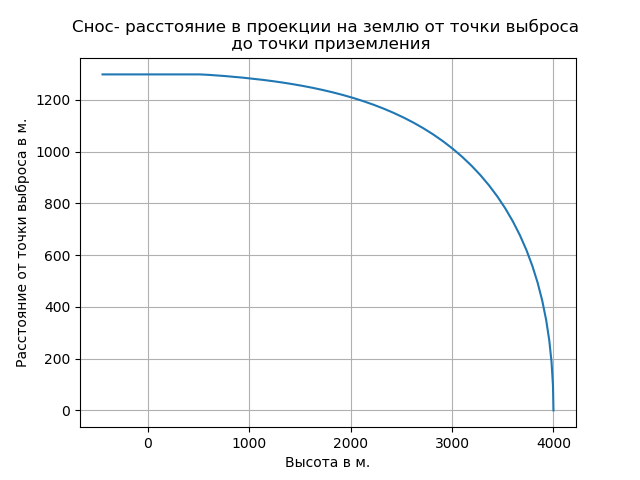
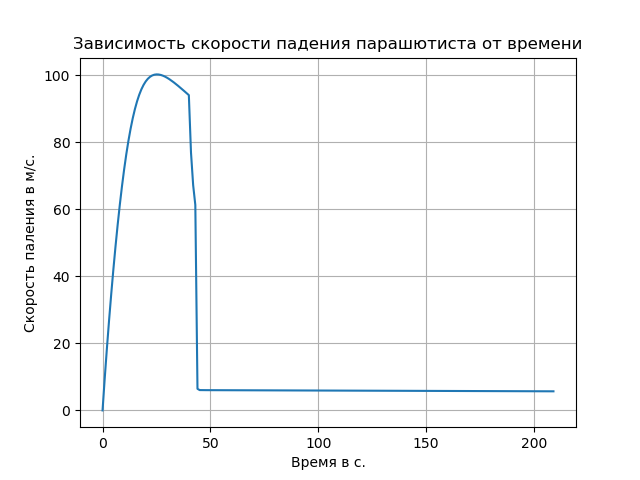
مع الأخذ في الاعتبار الهواء المتقطع أدى إلى زيادة في معدل السقوط الحر وغير طبيعة المسار في هذا القسم.

يمكن حل هذه المشكلة بمساعدة نظام من معادلتين تفاضليتين ، ترد أدناه (باستثناء المظلات والتغيرات في كثافة الهواء):

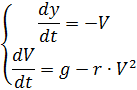
يظهر التغيير في قوى المقاومة وكثافة الهواء في القائمة تحت المفسد ، مع مراعاة ما ورد أعلاه ودون تفسير

# - * - الترميز: utf8 - * -
من استيراد numpy *
من scipy. Integrate استيراد odeint
استيراد matplotlib.pyplot بتنسيق plt
م = 100
ص 0 = 1.3
ج 1 = 0.3
ج 2 = 0.6
ج 3 = 0.5
ج 4 = 0.75
ق = 70
ق = 0.8
ss = 1.5
ز = 9.8
ملعقة شاي = 6
tsbp = 10
TP = 90.0
ح = 1000.0
بيتا = 1.25 * 10 ** - 4
ألفا = 6.5 * 10 ** - 3
T0 = 300
def ks (t):
إذا كانت t <tsp:
ض = 0
آخر:
ض = 1
عودة z
def ko (t):
إذا كانت t <tsp + tsbp:
ض = 0
آخر:
ض = 1
عودة z
# dy1 / dt = y2
# dy2 / dt = g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * ص 2 ** 2) / م
def f (y، t):
y1، y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0.5 * r * c1 * s
k2 = 0.5 * r * c2 * s
k3 = 0.5 * r * c3 * ss
k4 = 0.5 * r * c4 * S
ارجع [-y2، g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / م]
t = ترتيب (0.0 ، tp)
y0 = [ح ، 0.0]
[y1، y2] = odeint (f، y0، t، full_output = False) .T
plt.title ("القفز بالمظلات من 1000 و 800 متر")
plt.plot (y1، y2، label = 'Altitude 1000 m')
ح = 800.0
ملعقة شاي = 6
tsbp = 2
tp = 80.0
def ks (t):
إذا كانت t <tsp:
ض = 0
آخر:
ض = 1
عودة z
def ko (t):
إذا كانت t <tsp + tsbp:
ض = 0
آخر:
ض = 1
عودة z
def f (y، t):
y1، y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0.5 * r * c1 * s
k2 = 0.5 * r * c2 * s
k3 = 0.5 * r * c3 * ss
k4 = 0.5 * r * c4 * S
ارجع [-y2، g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / م]
t = ترتيب (0.0 ، tp)
y0 = [ح ، 0.0]
[y1، y2] = odeint (f، y0، t، full_output = False) .T
plt.plot (y1، y2، label = 'Height 800 m')
plt.xlabel ("الارتفاع بالأمتار")
plt.ylabel ("سرعة الاحتراق بـ m / s.)"
plt.legend (loc = 'best')
plt.grid (صحيح)
عرض plt.show ()

نحصل على:

الخلاصة

يتم تحديد الخصائص الباليستية الزمنية لحركة مركز كتلة الهبوط المظلي من طائرة.

المراجع

الضغط الجوي.
Gerasimenko I.A. التدريب المحمول جوا: كتاب مدرسي. م: النشر العسكري ، 1986. الجزء 1 ، ص 32.

تحديد الخصائص الباليستية الزمنية لحركة مركز كتلة الهبوط المظلي من طائرة