مقدمة

ستتحدث هذه المذكرة القصيرة عن كيفية بناء نموذج تشتت الضوء الجوي في آخر 4k int Appear by Jetlag ، والتي احتلت النسخة الحزبية مكانها الثاني عشر المشرّف في مقدمة 4k في حفل Revision 2018 التجريبي في أبريل من هذا العام.

يمكنك تنزيل البرنامج الثنائي مجانًا بدون SMS هنا .

ومع ذلك ، إذا لم يكن لديك Windows ، أو إذا لم يكن لديك بطاقة فيديو حديثة قوية ، فهناك أحمق مريح:

تمت كتابة الموسيقى لهذا العمل عن طريق استخدام 4klang . بقيت جميع الرموز والمرئيات ورائي.

هنا سنتحدث فقط عن نموذج تشتت الضوء. لا تتأثر أشياء أخرى ، مثل الأدوات ، ونموذج المدينة ، ونموذج الإضاءة والمواد. يمكنني إرسال الشجعان لقراءة المصدر ، أو مشاهدة تسجيلات كيف كنت أغرق لساعات - معظم التطوير كان على الفيديو.

قصة مملة تفوت

بدأ العمل في هذا العمل مع إدراك أن الوظيفة الرئيسية بدوام كامل لا تترك وقتًا للعمل على وظيفة كاملة الحجم من الدرجة الرابعة - إنها بالفعل في منتصف شهر مارس تقريبًا في الفناء ، وبقي أسبوعان حتى Revizen.
يبقى فقط أن يأتي بشيء بسيط بما يكفي لسرعة ، لبضع ليالي ، حشو كومبو. إن القيام بإعادة مسيرة غبية أخرى لا يعني احترام المشاهد ، لذلك تذكرت أنه قبل بضع سنوات كان علي أن أعمل تظليلًا مع التشتت ، وكان بسيطًا ومضغوطًا وفي نفس الوقت مسموحًا به جميلًا ، وإن كان بطيئًا إلى حد ما.

خلال مناقشة قصيرة ، أصررت بمفردي ، وقررنا التركيز على ما يلي: لجعل المناظر الطبيعية المليئة بالضوء المنتشر ، مع غروب الشمس والغيوم وأشعة الشفق (TIL كما يتم ترجمة عبارة "أشعة الله"). لكي لا ترفع عدد الخطوات في الغلاف الجوي إلى قيم غير تفاعلية تمامًا ، يجب عليك أن تهتز بشدة (مثل طريقة فناء مونتي كارلو) ، والتي ستولد ضوضاء مرئية. ولكن لا يهم إذا قمت بتحريك الكاميرا وتغيير المشهد ببطء وبدء المسار المحيط ، يمكنك مزج الإطارات المجاورة بشكل غير مؤلم وتخفيف هذه الضوضاء مؤقتًا.

كتب كين الموسيقى بسرعة كبيرة - كانت جاهزة تقريبًا قبل أسبوعين من المراجعة. ومع ذلك ، أصبت بالشلل الشديد بسبب الإنفلونزا - بسيارة إسعاف ومرض معدي - لذلك لم أبدأ عمليًا في العمل في تظليل حتى اللحظة التي وصلت فيها إلى الطائرة إلى فرانكفورت بطريقة أو بأخرى بطريقة أو بأخرى. لقد تم بالفعل كتابة النموذج الأولي لهذا النموذج المتناثر في الهواء.

لقد قمنا بخلط نسخة الحفلة من الرمل واللعاب في الحفلة نفسها للساعات القليلة المتبقية قبل الموعد النهائي (وربما بعد بضع ساعات ؛ D) ، بينما كنت أبتعد في نفس الوقت عن الأنفلونزا ، وقلة النوم ، ورحلات لساعات طويلة ، و لقد كان مشتتًا باستمرار من خلال المشاركة في Compoing المواجهة Shader .

تحتوي النسخة المعروضة على الشاشة الكبيرة على الكثير من القطع الأثرية وفقط الهندسة البدائية للمدينة بناءً على مخطط Voronoi مع ارتفاعات عشوائية.

بشكل عام ، المكان الثاني عشر سخي للغاية.

تم إصدار النسخة النهائية ، الموضحة أعلاه ، في وقت لاحق وفي وضع أكثر استرخاء ، من الساعة 1-2 مساءً في الأسبوع لمدة شهر. في المجموع ، استغرق العمل حوالي 40-50 ساعة.

نموذج التشتت

(ملاحظة: أنا لا أقوم ببرمجة الرسومات بشكل احترافي. هذه هوايتي الصغيرة المريحة للخير ، إذا تم إلغاء تركيز مائة أو اثنين تحت بيرة ساعات النبيذ سنويا. لذلك ، لا يوجد احتمال صفري أن يتم وصف بعض الأشياء أدناه و / أو تسميتها بشكل غير صحيح. العم ، ضرب!)

تم استعارة نموذج التشتت من مقالة "تشتت الضوء الخارجي عالي الأداء باستخدام أخذ العينات القطبية" بقلم إيجور يوسوف ، المنشور في كتاب GPU Pro 5 ، مع إخراج قطعي قطبي تمامًا.

النموذج المادي

تقصف فوتونات الشمس الغلاف الجوي للأرض وتتفاعل مع جزيئات الهواء. يمكن أن ينتشر الفوتون بواسطة جسيم ، مما يستلزم تغييرًا في اتجاه الفوتون ، أو يمكن امتصاصه ، مما يعني أن الفوتون مفقود ، وقد تم تحويل طاقته إلى شكل آخر.
كلتا العمليتين هي احتمالية وتعتمد بشكل خاص على كثافة الجسيمات وطاقة الفوتون (التي تتوافق مع لونها).

على الأصابع ، تتمتع الفوتونات "الحمراء" بفرصة أقل للتفاعل مع الهواء ، لذلك فهي تتغلب على سمك الغلاف الجوي سليمًا نسبيًا.
ومع ذلك ، فإن اللون الأزرق لديه احتمالية أعلى للتشتت ، وهذا هو السبب في أنه يمكنه تغيير الاتجاه بشكل متكرر والسفر مسافات كبيرة في الغلاف الجوي قبل أن يصل (أو لا) إلى المراقب.

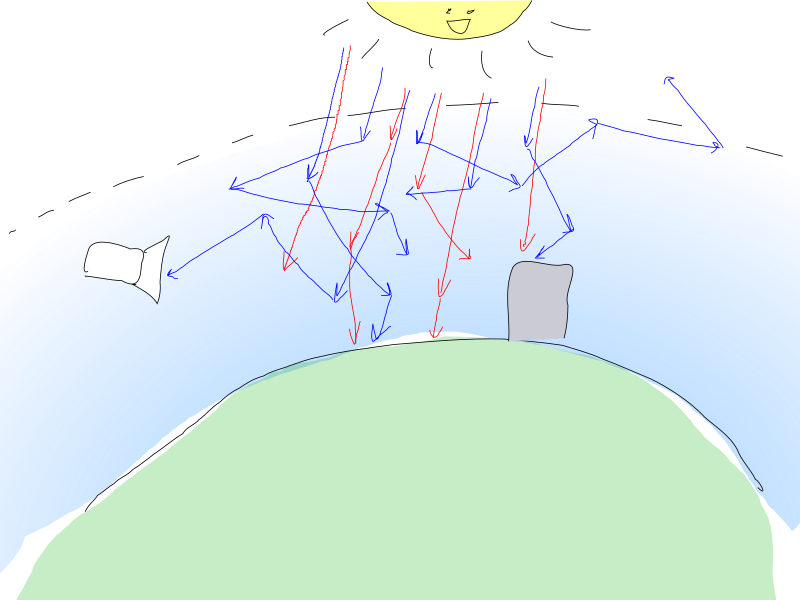
معلمات تفاعل الضوء مع الهواء التي تهمنا هي كما يلي:

• $$$\ beta ^ s (x)$ - جزء من الضوء المبعثر لكل وحدة طول عند نقطة $$$x$
• $$$\ beta ^ a (x)$ - جزء من الضوء الممتص لكل وحدة طول عند نقطة $$$x$
• $$$\ beta ^ e (x) = \ beta ^ s (x) + \ beta ^ a (x)$ - إجمالي جزء من الضوء المفقود لكل وحدة طول عند نقطة $$$x$
• $$$p (\ alpha)$ هو التوزيع الزاوي للضوء المتناثر حيث $$$\ alpha$ هذه هي الزاوية بين الشعاع الساقط والحادث

من المفترض أن الهواء يتكون من نوعين من الجسيمات ، وتناثرها يحدث بشكل مستقل: الجزيئات (نموذج Rayleigh) والهباء الجوي (الجسيمات الكروية الكبيرة نسبيًا ، تشتت Mie في أدب اللغة الإنجليزية). تختلف النماذج فقط في القيم المختلفة للمعلمات أعلاه.

لكلا النموذجين ، يعتقد أن كثافة الجسيمات المقابلة تتناقص بشكل كبير مع الارتفاع: $$$\ rho = \ rho_0e ^ {- \ frac {h} {H}}$ أين $$$\ rho_0$ - الكثافة عند مستوى سطح البحر. احتمالات $$$\ بيتا$ متناسب $$$\ rho$ ، وتعني معانيها أدناه لمستوى سطح البحر.

نموذج Rayleigh

• $$$p_R (\ alpha) = \ frac {3} {16 \ pi} (1+ \ cos ^ 2 (\ alpha))$ [نيشيتا وآخرون. 93 ، بريثام وآخرون. 99]
• $$$\ beta_R ^ a = 0$
• $$$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} = (5.8، 13.5، 33.1) _ {rgb} 10 ^ {- 6} m ^ {- 1}$ [رايلي وآخرون. 04 وبرونيتون ونيريت 08]
• $$$H_R = 7994 مليون دولا$ [نيشيتا وآخرون. 93]

الهباء الجوي

• $$$p_M (\ alpha) = \ frac {1} {4 \ pi} \ frac {3 (1-g ^ 2)} {2 (2 + g ^ 2)} \ frac {1+ \ cos ^ 2 (\ alpha)} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}}$ [نيسيتا وآخرون. 93 ، رايلي وآخرون. 04] أين $$$g = 0.76$ [برونيتون ونيريت 08]
• $$$\ beta_M ^ s = 2 \ cdot10 ^ {- 5} m ^ {- 1}$ [برونيتون ونيريت 08]
• $$$\ beta_M ^ e = 1.1 \ beta_M ^ s$
• $$ [نيشيتا وآخرون. 93]

تقريب تناثر واحد

يعتمد تقريب الانتثار على انبعاث شعاع من كل بكسل من الكاميرا وحساب مقدار الضوء من الغلاف الجوي الذي يجب أن يحصل من هذا الاتجاه. تتوافق كل شعاع مع جميع مكونات ضوء RGB الثلاثة ، كما لو أن ثلاثة فوتونات ذات طاقات مماثلة تطير على طول هذا الشعاع.

يتكون الضوء الذي يصل إلى الغرفة من خلال العمليات التالية في الهواء:

• التشتت (TIL الذي يتعلم التعرُّف كيفية ترجمة التشتت). يضاف الضوء المنبعث من الشمس ، والذي يتناثر بشكل احتمالي بزاوية تتوافق مع اتجاه الكاميرا.
• الامتصاص . يمتص الهواء الضوء الذي يحلق بالفعل على طول الشعاع.
• التشتت . يتم فقدان الضوء الذي يحلق بالفعل على طول الشعاع بسبب التشتت في اتجاهات أخرى.

لأسباب تتعلق بالأداء ، نعتقد أن الضوء يمكن أن يدخل فقط في اتجاه الكاميرا من التشتت مرة واحدة ، ويمكن إهمال كل الضوء الآخر (الذي كان مبعثرًا أكثر من مرة). لا ينصح بهذا للشفق ، ولكن ماذا تفعل.

يتم عرض هذا النهج في الصورة الجميلة التالية (حاولت!):

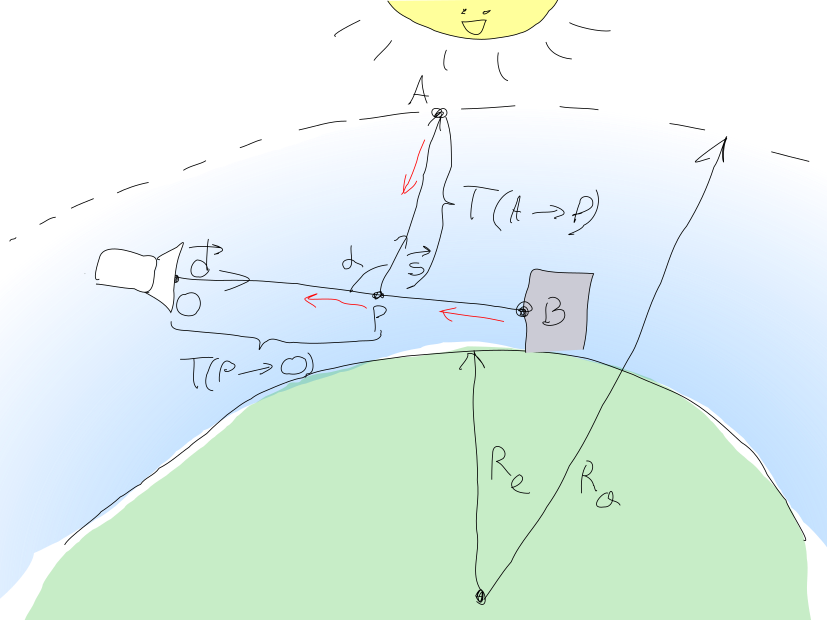
وبالتالي ، فإن مقدار الضوء الذي يجب الكشف عنه بواسطة بكسل الكاميرا عند $$$O$ يمكن حسابه كمجموع $$$\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {BO}}$ أين $$$\ mathbf {L_ {in}}$ - الضوء المنتشر من الشمس $$$\ mathbf {L_ {BO}}$ - مقدار الضوء من النقطة $$$B$ كائن هندسة المشهد تصل $$$O$ .

هندسة الضوء

$$$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {- \ mathbf {T} (B \ rightarrow O)}$ أين $$$\ mathbf {L_O}$ هو الضوء المنبعث من نقطة $$$B$ نحو الكاميرا.

$$$\ mathbf {T} (B \ rightarrow O)$ تسمى السماكة الضوئية للوسط بين النقاط $$$B$ و $$$O$ ، ويحسب على النحو التالي:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ int_B ^ O (\ beta_M ^ e (s) + \ mathbf {\ beta_R ^ e} (s)) ds$$

في حين أن الأعضاء $$$\ بيتا$ تتكون من ثبات مستوى البحر وكثافته المتغيرة ، ويمكن تحويل هذا التعبير إلى:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M (s) ds + \ mathbf {\ beta_R ^ e} \ int_B ^ O \ rho_R (s) ds = \ bar {\ mathbf {\ beta}} \ cdot \ bar {T_ \ rho} (B \ rightarrow O)$$

يرجى ملاحظة أنني لا أفصح على وجه التحديد $$$\ rho$ ، لأننا سنغيرها لاحقًا عند إضافة الغيوم. كما أود أن ألفت الانتباه إلى حقيقة ذلك $$$\ بيتا$ - ناقلات RGB (على الأقل $$$\ mathbf {\ beta_R}$ لها معان مختلفة لمكونات RGB ، و $$$\ beta_M$ - المتجه فقط من أجل الاتساق). الأعضاء مع $$$\ rho$ تحت التكامل توجد عددي.

أشعة الشمس

أشعة الشمس $$$\ mathbf {L_ {in}}$ تحسب بالتكامل على جميع النقاط $$$P$ على طول الجزء $$$Ob$ وتراكم جميع أشعة الشمس الواردة نحو الكاميرا والموت في السماكة $$$\ mathbf {T} (P \ rightarrow O)$ .

كمية ضوء الشمس التي تصل إلى نقطة $$$P$ يتم حسابها بواسطة صيغة مماثلة $$$\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {- T (A \ rightarrow P)}$ أين $$$\ mathbf {L_ {sun}}$ - سطوع الشمس و $$$A$ هي النقطة التي عندها الشعاع من النقطة $$$P$ نحو الشمس $$$\ vec {s}$ يترك الجو. جزء من هذا الضوء المنتشر نحو الكاميرا هو $$$\ mathbf {L_P} \ cdot (\ mathbf {\ beta_R ^ s} (s) p_R (\ alpha) + \ beta_M ^ s (s) p_M (\ alpha))$ .

المجموع الذي نحصل عليه:

$$

$$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P} (s) \ cdot (\ beta_M ^ s (s) p_M (\ alpha) + \ mathbf {\ beta_R ^ s} (s) p_R (\ alpha)) \ cdot e ^ {- \ mathbf {T} (P (s) \ rightarrow O)} ds$$

قد تلاحظ ما يلي:

• $$$\ alpha$ هو ثابت لكل شعاع بكسل للكاميرا (نعتقد أن الشمس بعيدة بشكل لا نهائي والأشعة منها متوازية)
• احتمالات $$$\ بيتا$ تتكون من ثوابت مستوى سطح البحر ووظائف الكثافة $$$\ rho (s)$
• وظائف $$$p (\ alpha)$ لها عوامل مشتركة لكل من عمليتي التشتت

هذا يسمح لك بتحويل التعبير إلى:

$$

$$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}} (1+ \ cos ^ 2 (\ alpha)) (\ frac {\ frac {1} {4 \ pi} \ frac {3 (1 -g ^ 2)} {2 (2 + g ^ 2)}} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}} \ beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R})$$

أين

$$

$$\ mathbf {I_M} = \ int_B ^ O \ rho_M (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) \ \ mathbf {T} (P (s) \ rightarrow O)} س$$

$$

$$\ mathbf {I_R} = \ int_B ^ O \ rho_R (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} س$$

$$$I_m$ و $$$I_R$ تختلف فقط في وظائف الكثافة ؛ الأس لها هي نفسها.

لم يتمكن أحد من حساب هذه التكاملات بشكل تحليلي ، لذلك يجب حسابها رقميًا باستخدام إعادة رسم الخرائط (كما يقولون في المنشورات الأصلية ، لا يمكنك القيام بذلك!).

التكامل العددي

لأسباب تتعلق بالحجم والكسل ، نفترض أنه غبي قدر الإمكان: $$$\ int_A ^ B f (x) dx \ almost \ frac {\ left | B - A \ right |} {N} \ sum_ {i = 0} ^ N f (A + i \ cdot \ frac {\ vec { B - A}} {N})$

سيتم تنفيذ مسيرة الشعاع في الاتجاه المعاكس لتيار الضوء: من نقطة الكاميرا $$$O$ قبل تقاطع الشعاع مع الهندسة $$$B$ . مقطع خط $$$O \ rightarrow B$ مقسومًا على $$$N$ خطوات.

قبل بدء المسيرة ، قم بتهيئة المتغيرات:

• vec2 ( vec2 منفصلان ، vec2 رايلي والهباء الجوي) السماكة البصرية المتراكمة الكلية $$$\ mathbf {T_ \ rho} (P (s) \ rightarrow O)$
• vec3 (RGB) $$$\ mathbf {I_M}$ ، $$$\ mathbf {I_R}$

التالي للنقطة $$$P_i$ بين كل خطوة $$$O$ و $$$B$ :

1. دعونا راي $$$\ vec {s}$ في اتجاه الشمس والحصول على نقطة $$$A_i$ خروج هذا الشعاع من الغلاف الجوي.
2. احسب السماكة $$$\ mathbf {T} (A \ rightarrow P_i)$ عن طريق الحساب الأول $$$\ int_A ^ {P_i} \ rho_M (s) ds$ و $$$\ int_A ^ {P_i} \ rho_R (s) ds$ باستخدام نفس عملية إعادة السير (بعدد الخطوات M ) ، ثم اضرب المصطلحات الناتجة في الثوابت المقابلة $$$\ beta_M ^ e$ و $$$\ mathbf {\ beta_R ^ e}$ .
3. احسب السماكة $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O) = \ mathbf {T_ \ rho} (P_ {i-1} \ rightarrow O) + \ rho_i (s) \ cdot ds$
4. تراكم $$$\ mathbf {I_R}$ و $$$\ mathbf {I_M}$ باستخدام هذه القيم

يتم حساب اللون النهائي بعد إعادة الترتيب من خلال مجموع المصطلحات:

1. مصطلح $$$\ mathbf {L_ {BO}}$ الحصول على تافه: متغير يحتوي $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O)$ يحتوي على قيمة $$$\ mathbf {T_ \ rho} (B \ rightarrow O)$ منذ ذلك الحين $$$P_i$ وصل $$$B$ .
2. عن طريق الضرب $$$\ mathbf {I_R}$ و $$$\ mathbf {I_M}$ إلى الثوابت المقابلة وإضافة النتيجة محسوبة $$$\ mathbf {L_ {in}}$

تظليل

تشتت بسيط بدون أي شخص

تمشيط وتعليق مصادر التشتت المأخوذة قليلاً (تقريبًا) مباشرةً من داخل نفسها:

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); } 

اخرس على التظليل

الغيوم

ليس سيئًا ، ولكن يمكن أيضًا الحصول على مثل هذه الصورة بسهولة أكبر مع بعض كومة التدرجات الماكرة.

بطريقة خادعة ، فإن الحصول على السحب وأشعة الله أكثر صعوبة. دعنا نضيف.

والفكرة هي تقريب الغيوم مع الهباء الجوي وتعديل كثافة الكثافة فقط densitiesRM() . قد لا يكون هذا صحيحًا جسديًا كما نود (ليس لدي أي فكرة عن كيفية اقتراب الضوء في السحب في رسومات الكمبيوتر).

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; } 

على عكس التوقعات ، لا نحصل على غيوم جميلة ، ونصر حلو ومعجبين ، ولكن قطع أثرية. محاولة رفع عدد القطع الأثرية على الجبهة لا تزيل تمامًا ، ولكنها تفسد الأداء بشكل ملحوظ.

الحلول العكازات التي تدفع داخل:

• معظم القطع الأثرية غير السارة في الأفق تختبئ خلف الجبال
• تتم إضافة الغيوم فقط بالقرب من الكاميرا.
• تمت إضافة مونت كارلوفشينا ، ويتم تغيير كل شعاع مسير بتعويض عشوائي: for (float i = pixel_random.w; i < steps; ++i) . هذا يضيف إلى الضجيج الذي عليك أن تخففه مؤقتًا من خلال مزج الإطارات المتتالية.

• يتزايد عدد خطوات المناطق التي تتطلب مزيدًا من التفاصيل (على سبيل المثال ، طبقة بها سحب). ولهذا السبب يتم إجراء هذا الفصل السخيف للوظائف إلى scatterImpl() و scatterDepthInt() :

  
  

   //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.); 

  
  

   //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); } 

  
  

المحاذاة مع هندسة المشهد

نتيجة لإعادة رسم الخرائط التقليدية لوظائف المسافة والظل ، تم بالفعل الحصول على المسافة من L إلى النقطة B ولون البكسل Lo . يتم استبدال هذه القيم ببساطة في دالة scatter() . إذا لم تستقر الحزمة على الهندسة وتركت المشهد ، فإن اللون Lo صفر ، L حساب L باستخدام escape() - يُعتقد أن الشعاع قد غادر الغلاف الجوي.

مثل كل شيء.

... في الواقع ، بالطبع ، ليس كل شيء. من المؤلم جدًا أن تحك جميع الأجزاء معًا بحيث تبدو قابلة للتصديق ككل. مجرد مجموعة من الضجة مع معلمات التواء ، هندسة المشهد ، وظائف الضوضاء ، المسار وزاوية الكاميرا. أخشى أنه ليس لدي نصيحة جيدة هنا ، باستثناء التكرار على مدار عدة ساعات وضرب رأسي بالحائط.

التصغير

بعد معالجة مصغر التظليل ، يكون حجم مبعثر تظليل النهائي حوالي 1500 بايت. يقوم Crinkler بضغطه إلى 700 بايت تقريبًا ، وهو ما يمثل حوالي 30 ٪ من جميع كود التظليل.

تربية

أنا لا أعرف كيف رسومات الحاسوب.