نموذج الانحدار متعدد الحدود

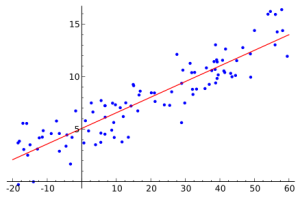
بعبارات بسيطة ، تم بناء نموذج الانحدار في الإحصائيات الرياضية على أساس البيانات المعروفة ، وهي أزواج من الأرقام. يتم تحديد عدد هذه الأزواج مسبقًا. إذا كنت تتخيل أن الرقم الأول في زوج هو قيمة الإحداثيات $$$x$ والثاني $$$y$ ، ثم يمكن تمثيل مجموعة أزواج الأرقام هذه على المستوى في نظام الإحداثيات الديكارتية كمجموعة من النقاط. لا يتم أخذ هذه الأزواج من الأرقام بشكل عشوائي. في الممارسة العملية ، كقاعدة ، يعتمد الرقم الثاني على الأول. إن بناء الانحدار يعني التقاط خط (بتعبير أدق ، دالة) يقترب من أقرب نقطة ممكنة (تقريبًا) الكثير من النقاط المذكورة أعلاه.

ما كل هذا؟ بادئ ذي بدء ، هذا ضروري لإعداد ما يسمى ب التوقعات. غالبا ما تحتاج إلى معرفة ذلك $$$y$ مع العلم فقط $$$x$ إذا كانت تختلف عن تلك X ، التي تم بناء الانحدار على أساسها. سأعطي مثالا بسيطا. هناك إحصائيات حول اعتماد نمو الشخص على عمره بناءً على 100 شخص مختلف تمت دراستهم. وبالتالي ، لدينا 100 زوج من الأرقام {العمر ؛ النمو}. في الوقت نفسه ، "النمو" هو كمية تابعة ، و "العمر" مستقل. من خلال بناء نموذج الانحدار بشكل صحيح ، يمكننا "التنبؤ" بالنمو بأي يقين بأي قيمة عمرية.

في الممارسة العملية ، اعتمادًا على الحالة ، يتم استخدام الأنواع الخطية ، والقطعية المكافئة ، والطاقة وأنواع أخرى من الوظائف في بناء نماذج الانحدار. في سياق الإحصائيات الرياضية ، غالبًا ما يتم النظر في نموذج الانحدار الخطي. في بعض الأحيان يتطرقون إلى حالة أكثر تعقيدًا - نموذج مكافئ. من خلال التعميم ، من السهل تخمين أن النماذج الخطية والقطع المكافئ هي حالات خاصة لنموذج أكثر تعقيدًا - متعدد الحدود. إن بناء نموذج انحدار يعني إيجاد معلمات الوظيفة التي ستظهر فيها. للانحدار الخطي - معلمتان: المعامل والمصطلح الحر.

يمكن استخدام الانحدار متعدد الحدود في الإحصائيات الرياضية لنمذجة مكونات الاتجاه للسلسلة الزمنية. السلسلة الزمنية هي في الواقع سلسلة من الأرقام التي تعتمد على الوقت. على سبيل المثال ، متوسط ​​درجة الحرارة اليومية للعام الماضي ، أو الدخل الشهري للشركة. يتم تقييم ترتيب كثير الحدود المحاكي بطرق خاصة ، على سبيل المثال ، بواسطة معيار السلسلة. الهدف من بناء نموذج للانحدار متعدد الحدود في مجال السلاسل الزمنية لا يزال هو نفسه - التنبؤ.

بادئ ذي بدء ، نعتبر مشكلة الانحدار متعدد الحدود بطريقة عامة. تستند جميع الاستدلال على تعميم المنطق في مشاكل الانحدار الخطي والمكافئ. بعد هذه الاعتبارات ، سأنتقل إلى حالة خاصة - النظر في هذا النموذج للسلسلة الزمنية.

دعونا نعطي سلسلتين من الملاحظات $$$x_i$ (متغير مستقل) و $$$y_i$ (متغير تابع) $$$i = \ overline {1، n}$ . معادلة كثير الحدود لها الشكل

$$

$$y = \ sum \ limits_ {j = 0} ^ k b_jx ^ j، \ \ \ \ \ (1)$$

أين $$$b_j$ - معلمات هذا كثير الحدود ، $$$j = \ overline {0، k}$ . من بينها $$$b_0$ - عضو مجاني. دعونا نجد معلمات المربعات الصغرى (OLS) $$$b_j$ نظرا للانحدار.

قياسا على الانحدار الخطي ، يعتمد OLS أيضًا على تقليل التعبير التالي:

$$

$$S = \ sum \ limits_ {i = 1} ^ n \ left (\ hat y_i-y_i \ right) ^ 2 \ to \ min \ \ \ \ \ (2)$$

هنا $$$\ hat y_i$ - القيم النظرية التي هي قيم كثيرات الحدود (1) عند النقاط $$$x_i$ . استبدال (1) في (2) نحصل عليه

$$

$$S = \ sum \ limits_ {i = 1} ^ n \ left (\ sum_ {j = 0} ^ kb_jx_i ^ j-y_i \ right) ^ 2 \ to \ min.$$

بناءً على الشرط اللازم لأقصى حد للوظيفة $$$(k + 1)$ المتغيرات $$$S = S (b_0 ، b_1 ، \ dots ، b_k)$ نحن نساوي مشتقاته الجزئية بالصفر ، أي

$$

$$S '_ {b_p} = 2 \ sum \ limits_ {i = 1} ^ nx_i ^ p \ left (\ sum \ limits_ {j = 0} ^ kb_jx_i ^ j-y_i \ right) = 0، \ \ \ p = \ overline {0، k}.$$

بتقسيم الجانبين الأيسر والأيمن لكل المساواة على 2 ، نكشف عن المجموع الثاني:

$$

$$\ sum \ limits_ {i = 1} ^ nx_i ^ p \ left (b_0 + b_1x_i + b_2x_i ^ 2 + \ dots + b_kx_i ^ k \ right) - \ sum \ limits_ {i = 1} ^ nx_i ^ py_i = 0 ، \ \ \ p = \ overline {0، k}.$$

فتح الأقواس ، ننقل في كل منهما $$$p$ التعبير العاشر ، المصطلح الأخير مع $$$y_i$ لليمين وتقسيم الجانبين $$$n$ . نتيجة لذلك ، حصلنا عليها $$$(k + 1)$ تعبيرات تشكل نظام المعادلات الخطية العادية ل $$$b_p$ . لديها الشكل التالي:

$$

$$\ left \ {\ start {array} {l} b_0 + b_1 \ overline x + b_2 \ overline {x ^ 2} + \ dots + b_k \ overline {x ^ k} = \ overline y \\ b_0 \ overline x + b_1 \ overline {x ^ 2} + b_2 \ overline {x ^ 3} + \ dots + b_k \ overline {x ^ {k + 1}} = \ overline {xy} \\ b_0 \ overline {x ^ 2} + b_1 \ overline {x ^ 3} + b_2 \ overline {x ^ 4} + \ dots + b_k \ overline {x ^ {k + 2}} = \ overline {x ^ 2y} \\ \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \\ b_0 \ overline {x ^ k} + b_1 \ overline {x ^ {k + 1}} + b_2 \ overline {x ^ {k + 2}} + \ dots + b_k \ overline {x ^ {2k}} = \ overline {x ^ ky} \ end {array} \ right. \ \ \ \ \ (3)$$

يمكنك إعادة كتابة النظام (3) في شكل مصفوفة: $$$AB = C$ أين

$$

$$A = \ left (\ start {array} {ccccc} 1 & \ overline x & \ overline {x ^ 2} & \ ldots & \ overline {x ^ k} \\ \ overline x & \ overline {x ^ 2 } & \ overline {x ^ 3} & \ ldots & \ overline {x ^ {k + 1}} \\ \ overline {x ^ 2} & \ overline {x ^ 3} & \ overline {x ^ 4} & \ ldots & \ overline {x ^ {k + 2}} \\ \ vdots & \ vdots & \ vdots & \ ddots & \ vdots \\ \ overline {x ^ k} & \ overline {x ^ {k + 1} } & \ overline {x ^ {k + 2}} & \ ldots & \ overline {x ^ {2k}} \ end {array} \ right)، \ \ B = \ left (\ start {array} {c} b_0 \\ b_1 \\ b_2 \\\ vdots \\ b_k \ end {array} \ right) ، \ \ C = \ left (\ start {array} {c} \ overline y \\\ overline {xy} \\ \ overline {x ^ 2y} \\\ vdots \\\ overline {x ^ ky} \ end {array} \ right).$$

ننتقل الآن إلى تطبيق الحقائق المذكورة أعلاه في حالة السلاسل الزمنية. دعونا نعطي سلسلة زمنية $$$x_t$ أين $$$t = \ overline {1، n}$ . مطلوب لبناء اتجاه النظام متعدد الحدود $$$k$ والذي يقارب السلاسل الزمنية المحددة بأكبر قدر ممكن من الدقة. كمتغير مستقل $$$x$ سنتخذ $$$t$ بناء على تعريف السلاسل الزمنية. هذه Xs هي سلسلة من الأرقام الطبيعية التي تشير إلى فترة زمنية. ك $$$y$ يتم أخذ قيم السلاسل الزمنية $$$x_t$ . يمكن ملاحظة أن قيم العناصر $$$a_ {ij}$ مصفوفات النظام $$$A$ بغض النظر عن $$$x_t$ . لأنه في الحالة العامة ، من الواضح ،

$$

$$a_ {ij} = \ overline {x ^ {i + j-2}} = \ frac1n \ sum \ limits_ {r = 1} ^ nx_r ^ {i + j-2} ،$$

ثم في حالة السلاسل الزمنية

$$

$$a_ {ij} = \ frac1n \ sum \ limits_ {r = 1} ^ nr ^ {i + j-2} ،$$

أين $$$i، j = \ overline {1، (k + 1)}.$

العناصر $$$c_j$ ناقلات مصفوفة المصطلحات الحرة $$$C$ تم الحصول عليها بشكل عام

$$

$$c_j = \ overline {x ^ {j-1} y} = \ frac1n \ sum \ limits_ {r = 1} ^ nx_r ^ {j-1} y_r.$$

وفي حالة السلاسل الزمنية

$$

$$c_j = \ frac1n \ sum \ limits_ {r = 1} ^ nr ^ {j-1} x_r،$$

أين $$$j = \ overline {1، (k + 1)}.$

وبالتالي ، بعد حل النظام (3) ، يمكننا العثور على المعلمات المطلوبة لاتجاه كثير الحدود $$$b_0 ، \ dots ، b_k.$

لملء مصفوفات النظام وحلها ، يمكن استخدام إحدى الطرق العددية عند نمذجة اتجاه على الكمبيوتر. في هذه الحالة ، ستكون نتيجة الحساب دقيقة للغاية.

ونتيجة لذلك ، سيأخذ عنصر الاتجاه الشكل التالي:

$$

$$T_t = \ sum \ limits_ {i = 0} ^ kb_it ^ i، \ \ \ t = 0،1،2، \ dots.$$

ومن الجدير بالذكر أيضًا أن عنصر الاتجاه المحاكي $$$T_t$ ، تم تحديده ليس فقط للفترات الحالية $$$[1؛ n]$ ، ولكن أيضًا للفترات المستقبلية $$$t> n$ .

ألاحظ على الفور أن نماذج الانحدار متعدد الحدود هي فقط عنصر الاتجاه في السلسلة الزمنية. يتضمن نموذج سلسلة زمنية كاملة أيضًا مكونات أخرى ، والتي تتجاوز نطاق هذه المقالة.

في الممارسة العملية ، أنا شخصياً لم أر سلسلة زمنية بترتيب اتجاه متعدد الحدود أكثر من 2. وهذا يفسر انتشار نماذج الانحدار الخطي والتمثيل الغذائي كحالات معينة من كثيرات الحدود.