إذا كنت تصف في جملتين ما هو مبدأ عمل تبادل الفرز ، ثم:

1. تتم مقارنة عناصر الصفيف في أزواج
2. إذا كان العنصر الموجود على اليسار ^* أكبر من العنصر الموجود على اليمين ، فسيتم تبديل العناصر
3. كرر الخطوات من 1-2 حتى يتم فرز الصفيف

^{* - العنصر الموجود على اليسار يعني ذلك العنصر من الزوج المقارن ، والذي يكون أقرب إلى الحافة اليسرى للصفيف. وفقًا لذلك ، يكون العنصر الموجود على اليمين أقرب إلى الحافة اليمنى.}

أعتذر على الفور عن تكرار مادة معروفة جيدًا ، فمن غير المحتمل أن تكون واحدة على الأقل من الخوارزميات في المقالة بمثابة كشف لك. حول هذه الفرز على حبري ، تمت كتابته بالفعل عدة مرات (بما في ذلك أنا - 1 ، 2 ، 3 ) ويسأل عن سبب العودة مرة أخرى إلى هذا الموضوع؟ ولكن منذ أن قررت كتابة سلسلة متماسكة من المقالات حول جميع الفرز في العالم ، يجب أن أذهب عبر طرق التبادل حتى في الإصدار السريع. عند النظر في الفئات التالية ، سيكون هناك بالفعل العديد من الخوارزميات الجديدة (وقليل من الناس يعرفون) التي تستحق مقالات منفصلة مثيرة للاهتمام.

تقليديا ، تشمل "المبادلات" الفرز الذي تتغير فيه العناصر (الزائفة) بشكل عشوائي (bogosort ، bozosort ، permsort ، إلخ). ومع ذلك ، لم أدرجهم في هذا الفصل ، لأنهم يفتقرون إلى المقارنات. سيكون هناك مقال منفصل حول هذه الفرز ، حيث نفلسف الكثير حول نظرية الاحتمالات ، التوافقية ، والموت الحراري للكون.

سخيفة نوع: Stooge الفرز

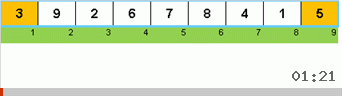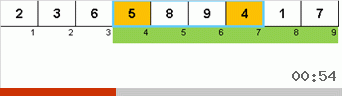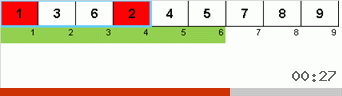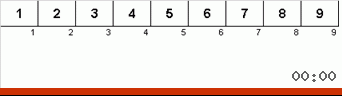
1. قارن (وإذا لزم الأمر التغيير) العناصر الموجودة في نهايات الصفيف.
2. نأخذ ثلثي المصفوفة الفرعية من بدايتها ونطبق الخوارزمية العامة على هذه 2/3 بشكل متكرر.
3. نأخذ ثلثي المصفوفة الفرعية من نهايتها ونطبق الخوارزمية العامة على هذه 2/3 بشكل متكرر.
4. ومرة أخرى ، نأخذ ثلثي المصفوفة الفرعية من بدايتها ونطبق الخوارزمية العامة على هذه 2/3 بشكل متكرر.

في البداية ، تعد المجموعة الفرعية مجموعة كاملة. ثم يقوم العودية بتقسيم المجموعة الفرعية الأم إلى 2/3 ، وإجراء مقارنات / تبادلات في نهايات الأجزاء المجزأة ، وترتيب كل شيء في النهاية.

def stooge_rec(data, i = 0, j = None): if j is None: j = len(data) - 1 if data[j] < data[i]: data[i], data[j] = data[j], data[i] if j - i > 1: t = (j - i + 1) // 3 stooge_rec(data, i, j - t) stooge_rec(data, i + t, j) stooge_rec(data, i, j - t) return data def stooge(data): return stooge_rec(data, 0, len(data) - 1) 

يبدو الفصام ، لكنه مع ذلك صحيح 100٪.

فرز بطيء :: فرز بطيء

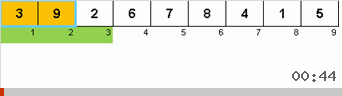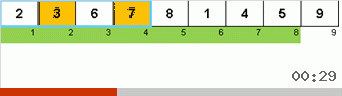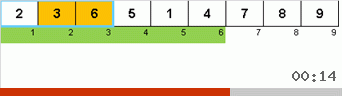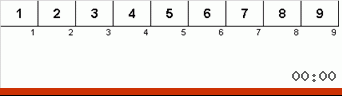
وهنا نلاحظ التصوف العودي:

1. إذا كانت المجموعة الفرعية تتكون من عنصر واحد ، فإننا نكمل العودية.
2. إذا كانت المجموعة الفرعية تتكون من عنصرين أو أكثر ، فقم بتقسيمها إلى نصفين.
3. نطبق الخوارزمية بشكل متكرر على النصف الأيسر.
4. نطبق الخوارزمية بشكل متكرر على النصف الأيمن.
5. تتم مقارنة العناصر الموجودة في نهايات الصفيف (ويتم تغييرها إذا لزم الأمر).
6. نقوم بتطبيق الخوارزمية بشكل متكرر على صفيف فرعي بدون العنصر الأخير.

في البداية ، يكون النطاق الفرعي هو الصفيف بأكمله. وسيستمر العودية إلى النصف والمقارنة والتغيير حتى يتم فرز كل شيء.

 def slow_rec(data, i, j): if i >= j: return data m = (i + j) // 2 slow_rec(data, i, m) slow_rec(data, m + 1, j) if data[m] > data[j]: data[m], data[j] = data[j], data[m] slow_rec(data, i, j - 1) def slow(data): return slow_rec(data, 0, len(data) - 1) 

يبدو هذا هراء ، لكن الصفيف أمر.

لماذا تعمل StoogeSort و SlowSort بشكل صحيح؟

سيطرح القارئ الفضولي سؤالًا معقولًا: لماذا تعمل هاتان الخوارزمتان حتى؟ يبدو أنها بسيطة ، ولكن ليس من الواضح جدًا أنه يمكنك فرز شيء من هذا القبيل.

دعونا نلقي نظرة أولاً على التصنيف البطيء. تشير النقطة الأخيرة من هذه الخوارزمية إلى أن الجهود العودية للفرز البطيء تهدف فقط إلى وضع أكبر عنصر في المصفوفة الفرعية في أقصى يمينها. يمكن ملاحظة ذلك بشكل خاص إذا قمت بتطبيق الخوارزمية على صفيف تم طلبه مسبقًا:



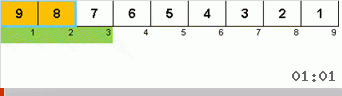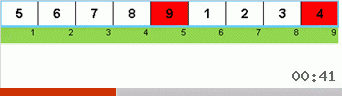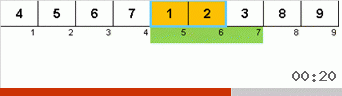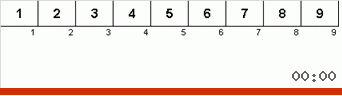
من الواضح أنه على جميع مستويات العودية ، تهاجر الحدود القصوى بسرعة إلى اليمين. ثم يتم إيقاف هذه الحدود القصوى ، حيث تكون هناك حاجة إليها ، من اللعبة: الخوارزمية تستدعي نفسها - ولكن بدون العنصر الأخير.

في فرز Stooge ، يحدث سحر مماثل:



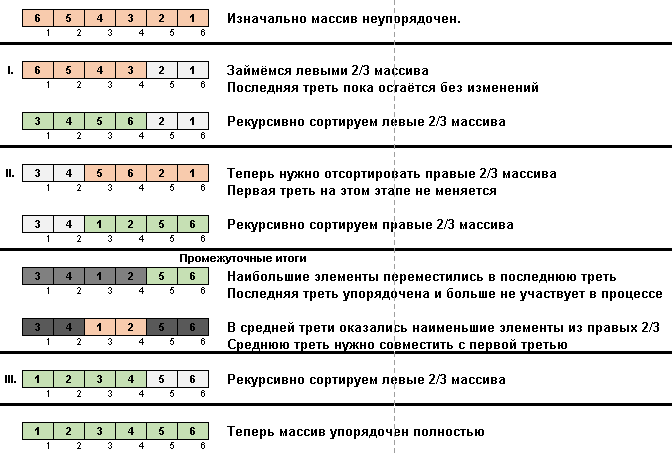
في الواقع ، يتم التركيز أيضًا على العناصر القصوى. ينقلها الفرز البطيء فقط إلى النهاية واحدًا تلو الآخر ، ويدفع فرز Stooge ثلث عناصر المصفوفة الفرعية (أكبرها) إلى الثلث الأيمن من مساحة الخلية.

ننتقل إلى الخوارزميات ، حيث كل شيء واضح بالفعل.

فرز غبي :: فرز غبي

فرز دقيق للغاية. ينتقل من بداية الصفيف إلى النهاية ويقارن العناصر المجاورة. إذا كان لا بد من تبادل عنصرين متجاورين ، فعندئذ فقط ، في حالة عودة الفرز إلى بداية المصفوفة ويبدأ من جديد.

 def stupid(data): i, size = 1, len(data) while i < size: if data[i - 1] > data[i]: data[i - 1], data[i] = data[i], data[i - 1] i = 1 else: i += 1 return data 

ترتيب جنوم :: فرز جنوم

نفس الشيء تقريبًا ، لكن الفرز أثناء التبادل لا يعود إلى بداية المصفوفة ، ولكنه يتراجع خطوة واحدة فقط. اتضح أن هذا يكفي لفرز كل شيء.

 def gnome(data): i, size = 1, len(data) while i < size: if data[i - 1] <= data[i]: i += 1 else: data[i - 1], data[i] = data[i], data[i - 1] if i > 1: i -= 1 return data 

محسن فرز القزم

ولكن يمكنك التوفير ليس فقط عند التراجع ، ولكن أيضًا عند المضي قدمًا. مع العديد من التبادلات المتتالية ، عليك أن تأخذ العديد من الخطوات إلى الوراء. ثم عليك العودة (مقارنة على طول العناصر التي تم ترتيبها بالفعل بالنسبة لبعضها البعض). إذا كنت تتذكر المركز الذي بدأت منه التبادلات ، فيمكنك القفز على الفور إلى هذا المركز عند اكتمال التبادلات.

 def gnome(data): i, j, size = 1, 2, len(data) while i < size: if data[i - 1] <= data[i]: i, j = j, j + 1 else: data[i - 1], data[i] = data[i], data[i - 1] i -= 1 if i == 0: i, j = j, j + 1 return data 

تصنيف الفقاعة: تصنيف الفقاعة

على عكس الفرز الغبي والساذج ، عند تبادل العناصر في الفقاعة ، لا تحدث أي عوائد - تستمر في المضي قدمًا. للوصول إلى النهاية ، يتم نقل أكبر عنصر في المصفوفة إلى النهاية.

ثم تكرر عملية الفرز العملية برمتها مرة أخرى ، ونتيجة لذلك يكون العنصر الثاني في الأقدمية في الأخير ولكن في مكان واحد. في التكرار التالي ، ثالث أكبر عنصر هو العنصر الثالث من النهاية ، إلخ.

 def bubble(data): changed = True while changed: changed = False for i in range(len(data) - 1): if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] changed = True return data 

أمثلية فرز الفقاعة

يمكنك تحقيق ربح بسيط على التمريرات في بداية المصفوفة. في هذه العملية ، يتم ترتيب العناصر الأولى بشكل مؤقت بالنسبة لبعضها البعض (هذا الجزء المصنف يتغير باستمرار في الحجم - فهو ينخفض ​​ويزيد). يتم إصلاح هذا بسهولة ومع تكرار جديد يمكنك ببساطة القفز فوق مجموعة من هذه العناصر.
_{(سأضيف التنفيذ المختبر في Python هنا بعد ذلك بقليل. لم يكن لدي الوقت لإعداده.)}

شاكر فرز :: فرز شاكر
(نوع كوكتيل :: نوع كوكتيل)

نوع من الفقاعة. في المرة الأولى ، كالمعتاد - ادفع الحد الأقصى حتى النهاية. ثم نستدير بشكل حاد ونضغط على الحد الأدنى إلى البداية. تزداد المساحة الهامشية المصنفة في الصفيف بعد كل تكرار.

 def shaker(data): up = range(len(data) - 1) while True: for indices in (up, reversed(up)): swapped = False for i in indices: if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] swapped = True if not swapped: return data 

الفرز الفردي: الفرز الفردي

مرة أخرى التكرارات حول المقارنة الزوجية للعناصر المجاورة عند الانتقال من اليسار إلى اليمين. أولاً فقط ، نقارن الأزواج التي يكون فيها العنصر الأول غريبًا في العد ، والثاني متساوي (أي الأول والثاني والثالث والرابع والخامس والسادس ، وما إلى ذلك). ثم العكس - حتى + فردي (الثاني والثالث والرابع والخامس والسادس والسابع وما إلى ذلك). في هذه الحالة ، تأخذ العديد من عناصر المصفوفة الكبيرة في تكرار واحد في نفس الوقت خطوة إلى الأمام (في الفقاعة ، يصل أكبر عنصر للتكرار إلى النهاية ، لكن بقية العناصر الكبيرة إلى حد ما تبقى في مكانها تقريبًا).

بالمناسبة ، كان هذا في الأصل نوعًا متوازيًا مع تعقيد O (n). سيكون من الضروري تطبيق AlgoLab في قسم "الفرز الموازي".

 def odd_even(data): n = len(data) isSorted = 0 while isSorted == 0: isSorted = 1 temp = 0 for i in range(1, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 for i in range(0, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 return data 

مشط الفرز :: مشط الفرز

أنجح تعديل للفقاعة. تتنافس خوارزمية السرعة مع الفرز السريع.

في جميع الاختلافات السابقة ، قارنا الجيران. وهنا ، أولاً ، تعتبر أزواج العناصر على مسافة قصوى من بعضها البعض. في كل تكرار جديد ، تضيق هذه المسافة بشكل موحد.

 def comb(data): gap = len(data) swaps = True while gap > 1 or swaps: gap = max(1, int(gap / 1.25)) # minimum gap is 1 swaps = False for i in range(len(data) - gap): j = i + gap if data[i] > data[j]: data[i], data[j] = data[j], data[i] swaps = True return data 

فرز سريع :: فرز سريع

حسنًا ، خوارزمية التبادل الأكثر تقدمًا.

1. قسّم المصفوفة إلى نصفين. العنصر الأوسط هو المرجع.
2. ننتقل من الحافة اليسرى للصفيف إلى اليمين ، حتى نجد عنصرًا أكبر من العنصر المرجعي.
3. ننتقل من الحافة اليمنى للصفيف إلى اليسار حتى نجد عنصرًا أصغر من العنصر المرجعي.
4. نتبادل بين العنصرين الموجودين في النقطتين 2 و 3.
5. نستمر في تنفيذ البنود 2-3-4 حتى يحدث اجتماع نتيجة للحركة المتبادلة.
6. في نقطة التقاء ، تنقسم المصفوفة إلى قسمين. لكل جزء ، نقوم بتطبيق خوارزمية فرز سريع بشكل متكرر.

لماذا يعمل؟ على يسار نقطة الالتقاء ، توجد عناصر أصغر أو تساوي العنصر المرجعي. على يمين نقطة الالتقاء عناصر أكبر من المرجع أو تساويه. أي أن أي عنصر من الجانب الأيسر أقل من أو يساوي أي عنصر من الجانب الأيمن. لذلك ، عند نقطة الالتقاء ، يمكن تقسيم المصفوفة بأمان إلى صفين فرعيين وفرز كل مجموعة فرعية بطريقة مماثلة بشكل متكرر.

 def quick(data): less = [] pivotList = [] more = [] if len(data) <= 1: return data else: pivot = data[0] for i in data: if i < pivot: less.append(i) elif i > pivot: more.append(i) else: pivotList.append(i) less = quick(less) more = quick(more) return less + pivotList + more 

K-sort :: K-sort

في حبري ، نُشرت ترجمة لأحد المقالات ، والتي تشير إلى تعديل QuickSort ، الذي يتفوق على الترتيب الهرمي بمقدار 7 ملايين عنصر. بالمناسبة ، هذا في حد ذاته إنجاز مريب ، لأن الفرز الهرمي الكلاسيكي لا يحطم سجلات الأداء. على وجه الخصوص ، لا يصل تعقيدها المقارب تحت أي ظرف من الظروف إلى O (n) (سمة من سمات هذه الخوارزمية).

لكن الشيء مختلف. وفقًا لكود المؤلف الزائف (ومن الواضح أنه غير صحيح) ، لا يمكن بشكل عام فهم ما هي في الواقع الفكرة الرئيسية للخوارزمية. شخصيا ، لدي انطباع بأن المؤلفين هم بعض المحتالين الذين تصرفوا وفقًا لهذه الطريقة:

1. نعلن اختراع خوارزمية فائقة الفرز.
2. نعزز العبارة باستخدام رمز زائف غير عامل وغير مفهوم (مثل ، ذكي وواضح جدًا ، لكن الحمقى لا يزالون لا يفهمون).
3. نقدم الرسوم البيانية والجداول التي من المفترض أن توضح السرعة العملية للخوارزمية على البيانات الضخمة. نظرًا لنقص رمز العمل الفعلي ، لن يتمكن أي شخص حتى الآن من التحقق من هذه الحسابات الإحصائية أو دحضها.
4. ننشر هراء على Arxiv.org تحت ستار مقال علمي.
5. الربح !!!

ربما أتحدث عبثًا مع الناس وفي الواقع تعمل الخوارزمية؟ يمكن لأي شخص أن يشرح كيف يعمل k-sort؟

UPD اتهاماتي الكاسحة لفرز مؤلفي الاحتيال تبين أنها لا أساس لها :) اكتشفت طائرات المستخدم الرمز الزائف للخوارزمية ، وكتبت نسخة عمل في PHP وأرسلتها إلي في رسائل خاصة:

إعلان

لقد كانت كلها نظرية ، لقد حان الوقت للانتقال إلى الممارسة. المقالة التالية تختبر فرز التبادلات على مجموعات البيانات المختلفة. سنكتشف:

• ما هو الفرز الأسوأ - سخيفة ، مملة ، أو مملة؟
• هل تساعد التحسينات والتعديلات في فرز الفقاعة حقًا؟
• تحت أي ظروف تكون الخوارزميات البطيئة سريعة في QuickSort بسهولة؟

وعندما نكتشف الإجابات على هذه الأسئلة الأكثر أهمية ، يمكننا أن نبدأ في دراسة الفصل التالي - أنواع الإدراج.

المراجع

Excel-application AlgoLab ، الذي يمكنك من خلاله خطوة بخطوة عرض التصور لهذه الأنواع (وليس فقط هذه).

Wiki - Silly / Stooge ، Slow ، Dwarf / Gnome ، Bubble / Bubble ، Shaker / Shaker ، Odd / Even ، Comb / Comb ، Fast / Quick

سلسلة مقالات

• تطبيق Excel AlgoLab.xlsm
• أنواع التبادل
  • مقارنة فرز التبادل
• أنواع الإدراج
• فرز حسب التحديد
• دمج الأنواع
• فرز حسب التوزيع
• الفرز الهجين