ريتشارد هامينج: الفصل 17. المرشحات الرقمية - IV

"إن الهدف من هذه الدورة هو إعدادك لمستقبلك الفني."

مرحباً هابر. هل تتذكر المقال الرائع "أنت وعملك " (+219 ، 2442 إشارة مرجعية ، 393 ألف قراءة)؟

لذا فإن هامينغ (نعم ، نعم ، التدقيق الذاتي وتصحيح الذات رموز الشفرات ) لديه كتاب كامل مكتوب على أساس محاضراته. نحن نترجمها ، لأن الرجل يتحدث عن الأعمال.

هذا الكتاب لا يتعلق فقط بتكنولوجيا المعلومات ، إنه كتاب عن أسلوب التفكير لدى الأشخاص الرائعين بشكل لا يصدق. "هذه ليست مجرد تهمة للتفكير الإيجابي ، يصف الظروف التي تزيد من فرص القيام بعمل عظيم ".

لقد قمنا بالفعل بترجمة 24 فصلاً (من أصل 30). ونحن نعمل على إصدار ورقي.

الفصل 17. المرشحات الرقمية - الرابع

(شكرًا على الترجمة ، أندريه باخوموف ، الذي رد على مكالمتي في "الفصل السابق".) من يريد المساعدة في ترجمة الكتاب وتنسيقه ونشره - اكتب في بريد إلكتروني شخصي أو magisterludi2016@yandex.ru

والآن ننتقل إلى المرشحات العودية ، التي لها الشكل التالي:



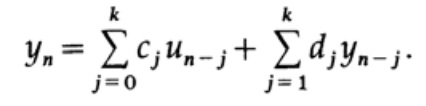
تظهر هذه الصيغة أن لدينا قيمًا على جانب واحد فقط من القيمة nth الحالية. نستخدم القيم السابقة للإشارة وقيمتها في الوقت الحالي un ، وكذلك القيم السابقة التي تم الحصول عليها عند إخراج المرشح.
هذا النهج الكلاسيكي هو نتيجة حقيقة أننا غالبًا ما نعالج الإشارة في الوقت الفعلي وليس لدينا إمكانية الوصول إلى قيم الإشارة المستقبلية.

بالإشارة إلى الأساسيات ، سنرى أنه إذا كانت لدينا "قيم مستقبلية" ، فربما يكون التنبؤ ثنائي الاتجاه أكثر دقة. بعد ذلك ، لحساب yn ، سنصادف نظامًا يحل على الفور المعادلات الخطية - لا بأس في عصر الحوسبة الرخيصة. سنترك هذه الملاحظة جانبًا ، غالبًا ما نسجل اليوم الإشارة على الشريط أو الوسائط الأخرى ، ثم نعالج البيانات في المختبر لاحقًا - وبالتالي لدينا قيم مستقبلية لبعض الوقت. على سبيل المثال ، قد يكون من الحماقة استخدام عامل تصفية رقمي متكرر في معالجة الصور لأنه لا يستخدم بعض المعلومات المتاحة ذات الصلة.

الجانب التالي الذي تحتاج إلى الانتباه إليه عند استخدام قيمة الإخراج السابقة كمدخل التالي هو وجود التعليقات - وهذا يثير تلقائيًا مسألة الاستقرار. هذا شرط يجب علينا مراقبته باستمرار أثناء تصميم المرشحات العودية. هذا يحد مما يمكننا القيام به. في هذه الحالة ، يعني الاستقرار أن تأثير الظروف الأولية لن يبدأ في الانتشار في النتيجة النهائية.

عند العمل مع نظام خطي ، رأينا أنه بغض النظر عن التردد الذي قمنا بتطبيقه على إدخال المرشح عندما يكون ثابتًا ، يظهر هذا التردد فقط عند خرج المرشح ، على الرغم من أنه يمكن تحويل مرحلة إشارة الخرج بالنسبة لطور الإشارة الأصلية. ومع ذلك ، في حالة الانتقال ، قد تظهر ترددات أخرى تنشأ عن حل معادلة تفاضلية متجانسة. المرشح العودي ليس أكثر من حل لمعادلة تفاضلية ذات معاملات ثابتة لمصطلحات un التي تشكل دالة تأثير.

لذلك ، بالنسبة لدولة ثابتة (تجاهل العابرين) ، نفترض ذلك



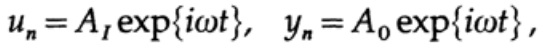
(حيث يمكن أن تكون A أرقامًا معقدة لتأخذ في الاعتبار تحول الطور) ، وهذا يؤدي إلى حل النسبة A0 / A1 للعثور على دالة التحويل:



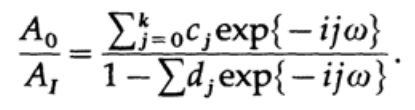
هذا التعبير هو دالة منطقية للمتغير المعقد exp {iωt} = z ، على عكس المرشح غير المتكرر الذي كان يُنظر إليه سابقًا ، حيث كانت خاصية النقل متعددة الحدود في z. تم تطوير الجزء النظري من تمثيل الوظيفة في شكل التوسع في سلسلة فورييه ؛ ولكن حتى الآن لا توجد نظرية حول تمثيل الوظائف كعلاقات لسلسلتين فورييه (أعتقد أنه لا توجد أسباب لعدم وجود مثل هذه النظرية). لذلك ، في الوقت الحالي ، ليست طرق التصميم منهجية (وهو ما فعله Kaiser لتصميم المرشحات غير العودية) ، بل هي مجموعة من الحيل.

وبالتالي ، لدينا مرشح بتروورث ، نوعان من مرشحات Chebyshev (اعتمادًا على وجود نفس التموج في نطاقات التمرير والتثبيط) ومرشح بيضاوي الشكل (والذي سمي بهذا الاسم بسبب استخدام الوظائف البيضاوية) ، والذي له نفس التموج في كلا النطاقين.



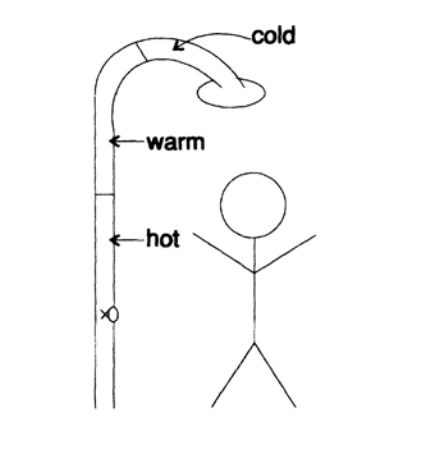الشكل 17.1

سوف أتطرق فقط إلى موضوع الملاحظات. لتوضيح مشكلة التعليقات ، سأخبرك قصة عني. ذات مرة ، شاركت في سلسلة من ستة برامج تلفزيونية مدتها نصف ساعة على أجهزة الكمبيوتر والحوسبة. تم التصوير بشكل رئيسي في سان فرانسيسكو. غالبًا ما بقيت هناك وكان لدي عادة البقاء في نفس الغرفة في نفس الفندق - من الرائع معرفة الغرفة بكل التفاصيل عندما تكون في وقت متأخر من الليل وتكون متعبًا أو عندما يكون عليك الاستيقاظ في منتصف الليل - ومن ثم الرغبة في البقاء في الغرفة.

من الرائع أن يقوم السباك بتوصيل الدش بأنابيب كبيرة (الشكل 17.I). ونتيجة لذلك ، في الصباح عندما بدأت في الاستحمام ، كان الماء باردًا جدًا ، وقمت بتحويل مقبض الصنبور بالماء الدافئ أكثر ، ولا يزال باردًا جدًا ، وأكثر ، ولا يزال باردًا جدًا ، وأكثر من ذلك ، وأخيرًا ، عندما حصلت المياه على درجة الحرارة المناسبة بقيت. بالطبع ، أصبح الماء أكثر سخونة وأكثر سخونة مع خروج الماء الذي دخل إلى الأنابيب سابقًا ، واضطررت إلى القفز من الحمام وحاول مرة أخرى للعثور على وضع مناسب لمقبض صنبور الماء الساخن. تسبب التأخير في توفير الماء الساخن في إزعاج. على الرغم من التجربة الغنية ، وجدت نفسي في وضع كلاسيكي من عدم الاستقرار. يمكنك النظر إلى هذا الموقف من أحد الجانبين: إما أن ردي كان قويًا جدًا (كنت وقحًا جدًا في أفعالي) أو كان الكشف عن الإشارة متأخرًا جدًا (كنت متسرعًا جدًا في ضبط الصنبور). نفس التأثير طويل الأمد! لم يكن عليّ أبدًا التعامل مع التأخيرات الطويلة من قبل ، لذلك بدأ صباحي كل يوم بإزعاج! في هذا المثال التوضيحي ، يمكنك إلقاء نظرة على جوهر عدم الاستقرار.

هنا لن أخوض في تصميم المرشحات العودية ، ألاحظ فقط أنه أثناء الصراع مع الصيغ التصحيحية للحل العددي للمعادلات التفاضلية العادية ، قمت بتطوير نظرية واحدة بشكل مستقل.

مصحح طريقة التنبؤ - مصحح لديه الشكل



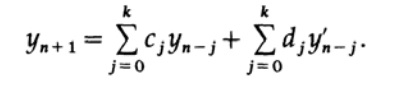
نرى الآن أن المعاملات uj للمرشح العودي هي المشتقات yn 'لإخراج المرشح ، المأخوذة من المعادلة التفاضلية. لا تحتوي المرشحات التقليدية غير العودية على حلقة تغذية مرتدة - لا تظهر قيم yn المحسوبة لاحقًا على الجانب الأيمن من التعبير. في المعادلات التفاضلية ، تظهر في كل من حلقة التغذية المرتدة ومشتقاتها ، وبالتالي تشكل حلقة تغذية مرتدة أخرى ، عادة غير خطية. لذلك ، يعد الاستقرار في مجال حل المعادلات التفاضلية موضوعًا أكثر تعقيدًا منه في مجال المرشحات العودية.

غالبًا ما تسمى هذه الفلاتر العودية "فلاتر ذات استجابة دافعة لانهائية" (فلاتر IIR) ، لأنه سيتم تكرار صدى اضطراب واحد من خلال حلقة التغذية المرتدة ، والتي سوف تتحلل بشكل كبير ، وفقط إذا كان المرشح مستقرًا. لن أكون نفسي إذا لم أتساءل عما إذا كان يجب أن تحتوي جميع الفلاتر العودية على هذه الخاصية. سرعان ما وجدت المثال المعاكس. في الحقيقة ، هذا ليس نوع المرشح الذي ستصممه عادةً ، لكن هذا المثال يظهر أن هذا البيان سطحي. إذا سألت نفسك عما إذا كان كل ما تقوله صحيحًا ، فستفاجأ بعدد الأشياء التي تصبح خاطئة ، حتى في المناطق المصممة جيدًا!

في الفصل 26 ، سأتناول مسألة العمل مع الخبراء. سترى الآن مثالاً لما يحدث كثيرًا. تم إخبار الخبراء بشيء ما في الفصل الدراسي عندما كانوا لا يزالون طلابًا ، ولم يسألوا أسئلة ، بل أخذوها على أنها حقيقة. وهم يعيدون إنتاج هذه الحقيقة المقبولة باستمرار دون محاولة التحقق مما إذا كانت صحيحة أم لا ، خاصة فيما يتعلق بالمشكلة التي يحاولون حلها في هذه اللحظة.

دعني أخبرك قصة أخرى الآن. كانت إحدى السيدات من قسم الرياضيات في مختبرات Labs Bella ترقص رقصة مربعة مع أحد الفيزيائيين في حفلة نهاية الأسبوع ، وفي صباح يوم الاثنين ، في الردهة ، ذكرت لي مشكلة كان يعاني منها. قام بقياس عدد النبضات في تجربة مشعة في كل مستوى ، على ما أذكر ، 256 مستوى طاقة. وهذا ما يسمى طيف العملية. كانت مشكلته الحصول على مشتق من البيانات.

لذا ، أنت تعلم أن (أ) عدد النبضات لمستوى معين من الطاقة سيشكل منحنى مع انقطاع ، و (ب) إن تمييزه للحصول على معامل الزاوية المحلية ليس مهمة سهلة في حد ذاته. كلما فكرت في مذكرتها العشوائية ، شعرت أكثر بالحاجة إلى مساعد جيد - وهذا هو أنا! لقد وجدته في دليل هاتف مختبرات بيل وأوضحت له اهتمامي وكيف وصلت إليه. أراد على الفور أن يأتي إلى مكتبي ، لكنني كنت عنيدًا وأصرت على الاجتماع في مختبره. حاول عرض مكتبه ، لكنني ما زلت أصر على مختبره. لماذا؟ من أجل تقييم قدراته وتقرير ما إذا كانت مشكلته تستحق وقتي وجهودي ، لأنها وعدت بأن تكون صعبًا للقضاء. اجتاز الاختبار ببراعة من قبل المختبر - أصبح من الواضح أنه كان مجربًا كفؤًا للغاية.

كان تقريبًا على وشك الحد من ما يمكنه فعله - تم جمع البيانات لمدة أسبوع ، وتم إخفاء مصدر الإشعاع بواسطة العديد من الشاشات. لا يبدو أنه يمكنك فعل أي شيء آخر لجمع بيانات أكثر دقة. علاوة على ذلك ، سرعان ما أصبحت مقتنعا ، على الرغم من أنني أعرف القليل من التفاصيل ، أن تجربته كانت مهمة للفيزياء وكذلك لمختبرات بيل. لذا ، توليت هذه المهمة. الأخلاق: إلى حد ما ، يمكنك الاختيار والعمل على تلك المهام التي تعتقد أنها مهمة.

من الواضح أن هذه كانت مشكلة تنعيم ، والواقع أن كايزر دربني للتو ، فما الذي يمكن أن يكون أفضل من إحضار المجرب إلى كايزر ومطالبة كايزر بتصميم مرشح تفاضلي مناسب؟ بدأت المشاكل على الفور. كان كايزر يفكر دائمًا في الإشارة كدالة للوقت ، والمنطقة تحت المنحنى كطاقة ، وفي هذه الحالة كانت الطاقة متغيرًا مستقلاً! عند هذه النقطة ، تكررت مشكلة كايزر حتى أخبرته مباشرة: "حسنًا ، طاقته قد حان الوقت ، وقياساته ، نبضاته ، هذا الجهد". فقط بعد ذلك كان Kaiser قادرًا على حل المشكلة.

تكمن لعنة الخبراء في فهمهم المحدود لما يمكنهم القيام به. ذكرت لك أن كايزر شخص قادر للغاية ، لكن تجربته ، كما يحدث غالبًا مع الخبراء ، حددت رؤيته. هل يمكنك ، بدوره ، أن تقوم بعمل أفضل؟ آمل أن تساعدك هذه القصص على تجنب هذا الفخ.

كما لاحظت سابقًا ، غالبًا ما يكون طيف الإشارة المفيدة في أسفل نطاق Nyquist ، ويتم توزيع طيف الضوضاء في جميع أنحاء نطاق Nyquist ، لذلك كان علينا العثور على تردد القطع بين الإشارة المفيدة للفيزيائي والضوضاء البيضاء المسطحة. كيف تجدها؟ في البداية ، جربت نموذجًا نظريًا للتجربة من رأس الفيزيائي الذي كان في رأسه - كان هناك الكثير من الخطوط الطيفية الضيقة في شكل وظائف غوسية فوق وظيفة غوسية واسعة (شككت في أن هذا كان توزيع كوشي ، لكن لم أجادل فيه ، لأن الاختلاف ستكون صغيرة جدًا ، نظرًا لطبيعة البيانات التي لدينا). لذا ، قمنا بمحاكاة هذا التوزيع ، وأعد كمية معينة من البيانات الاصطناعية المقابلة لهذا النموذج. أظهر التحليل الطيفي السريع للإشارة من خلال تحويل فورييه السريع أن الإشارة تقع في النصف السفلي من نطاق Nyquist. علاوة على ذلك ، قمنا بمعالجة بياناته التجريبية بنفس الطريقة وحصلنا على نفس موقع تردد القطع! يا له من حظ! (ربما يجب أن يعزى الحظ إلى مهارة المجرب). ذات مرة ، اجتمعت النظرية والممارسة! اتضح أننا استطعنا تصفية 95٪ من الضوضاء. أخيرًا ، كتب كايزر برنامجًا قام بتوليف مرشحًا لتردد قطع معين ، تم تعيينه من قبل المجرب.

قام البرنامج (1) بحساب عامل تصفية تفاضلي مناسب ، (2) كتب برنامجًا لحساب المخرجات السلسة ، ثم (3) قام بمعالجة البيانات باستخدام هذا المرشح دون أي تدخل من الفيزيائي.

لاحقًا ، قابلت فيزيائيًا من خلال تعديل تردد القطع لأجزاء مختلفة من بيانات مستوى الطاقة التي تم الحصول عليها في سلسلة واحدة من القياسات واضطررت إلى تذكيره بأن هناك "درجات حرية" معينة وما يفعله ليس معالجة بيانات صادقة. أصبح الأمر أكثر إشكالية عندما كانت الأمور تسير على ما يرام ، لإقناعه بالحصول على أقصى استفادة من بياناته (التي كان الحصول عليها مكلفًا للغاية) - يجب عليه العمل مع الجذور التربيعية لنبضاته ، حيث كان لديهم نفس التباين. أخيرًا ، فهم هذا وفعل ذلك. كتب هو وقيصر عملًا كلاسيكيًا في هذا المجال فتح الباب لأشياء جديدة يمكن القيام بها.

مساهمتي بشكل أساسي ، حدد المشكلة أولاً ، ثم اجمع الأشخاص المناسبين معًا ، ثم شاهد Kaiser لمواجهته بحقيقة أن التصفية ضرورية ليس فقط للإشارات كوظائف للوقت ، وأخيرًا أذكرهم بما عرفوه من الإحصائيات (أو يجب أن يكون لديهم أن يعرفوا ، ولكن ربما لم يعرفوا).

على أساس مني ، يبدو لي أن الحاجة إلى مثل هذا الدور تزداد عندما يصبح الناس خبراء أكثر عمقًا في مجالات المعرفة الضيقة بشكل متزايد. يحتاج شخص ما إلى الحفاظ على آفاق واسعة والتأكد من أن الأمور تتم بصدق. أعتقد أنني جئت إلى هذا الدور بعد تعليم طويل جدًا تحت قيادة جون توكي بالإضافة إلى أساس جيد في شكل أداة عالمية للعلوم تسمى الرياضيات. سأتحدث عن طبيعة الرياضيات في الفصل 23 .

تأتي معظم معالجة الإشارات من الإشارات بمرور الوقت. في الوقت نفسه ، تم تصميم معظم المرشحات الرقمية للدراسات الصغيرة المتخصصة للغاية التي لا ترتبط بالضرورة بالإشارات بمرور الوقت. هنا سأطلب منك أن تكون حذرا في المستقبل. لنفترض أنك تدير نشاطًا تجاريًا في القمة وتهتم بالبيانات التي توضح تكاليف العمالة السابقة للمعدات. ستكون البيانات صاخبة ، لكنك ما زلت تريد أن تفهم ، بالمعنى المعتاد ، ما يحدث في المؤسسة - ما هي العمليات طويلة المدى التي تحدث - تلك التي تكون بطيئة جدًا بحيث يفهمها الناس عندما تحدث بالفعل ، ولكن مع ذلك فهم وهو أمر مهم بشكل أساسي إذا كنت تريد أن تكون مديرًا جيدًا. ستحتاج إلى مرشح رقمي لتنعيم البيانات والاطلاع على تلميحات للاتجاه ، إن وجدت. أنت لا تريد العثور على اتجاه غير موجود ، ولكن إذا كان موجودًا ، فأنت تريد حقًا معرفة ما كان عليه من قبل للتنبؤ بما قد يكون عليه في المستقبل القريب. في الواقع ، سترغب في رؤية التغييرات في منحدر الاتجاه ، إذا كانت البيانات تسمح لك برؤيته. بعض الإشارات ، مثل قوة النيران فيما يتعلق بإزاحة السفينة ، ليست مرتبطة بالوقت ، ولكنها يمكن أن تخبرك كثيرًا عن الوضع الحالي للأسطول. بالطبع ، يمكنك دراسة هذه العلاقة كدالة للوقت.

في الجزء العلوي من حياتك المهنية ، ستكون قادرًا على استخدام مجموعة متنوعة من المرشحات الرقمية منخفضة المستوى للإشارات كدالة للوقت ، وليس فقط لإدارة الأشياء بشكل أفضل. لذلك ، أجادل بأنك ربما تقوم بتركيب المزيد من المرشحات الرقمية لمثل هذه الأشياء غير القياسية من تقليص بيانات الرادار والتطبيقات الكلاسيكية المماثلة. عادة في التطبيقات الجديدة للمعرفة يمكنك الحصول على أكبر عائد.

اسمحوا لي أن أعبر عن بعض المخاوف بشأن الاستخدام غير الصحيح للأدوات الذكية ؛ بمزيد من التفصيل ، سأتحدث عن مواضيع قريبة من الإحصائيات في الفصل 27 . يفترض تحليل توسع فورييه خطية النموذج الأساسي. يمكنك استخدامه للحالات غير الخطية قليلاً ، ولكن في أغلب الأحيان ، يفشل التحليل الذي تم إجراؤه بمهارة من خلال توسيع فورييه ، لأن الظاهرة التي تم التحقيق فيها غير خطية في طبيعتها. رأيت كيف تم إهدار الملايين من الدولارات عندما كان من الواضح جدًا للغرباء أن اللاخطية من شأنها أن تشوه التحليل الخطي الكامل الذي يتم عن طريق تقريب سلسلة فورييه. عندما أشاروا إلى ذلك ، كان جوابهم أنهم لا يعرفون ما هو النهج الآخر الذي يمكن اتخاذه ، لذلك استمروا في فعل الشيء الخطأ! وأنا لا أبالغ هنا.



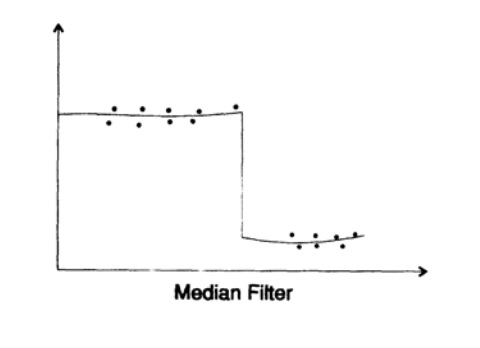الشكل 17.2

ماذا عن المرشحات غير الخطية؟ الاحتمالات هنا لا حصر لها وتعتمد بالطبع على المشكلة التي تتعامل معها. سأتعامل مع واحد منهم فقط ، مرشح متوسط.يمكنك التفكير في إخراج المرشح الوسيط لمجموعة بيانات محددة. دعونا نرى كيف يعمل في الممارسة. بادئ ذي بدء ، نلاحظ أنه يسعى إلى تخفيف أي ضوضاء محلية ، ولكن كيف سيتصرف المرشح عند نقطة الانقطاع (الشكل 17.2)؟

مع وجود عدد فردي من الأعضاء في المرشح الوسيط ، سترى أن إخراج المرشح يبقى في المستوى العلوي حتى أكثر من نصف النقاط عند إدخال المرشح في المستوى الأدنى ، وبعد ذلك "يقفز" إخراج المرشح لأسفل. سيتابع الفواصل جيدًا بما فيه الكفاية ولن يحاول تلطيفها تمامًا! في بعض الحالات ، هذا هو بالضبط نوع المرشح الذي يناسبك - يتم تخفيف الضوضاء المحلية ، بينما لن تضيع التغييرات المفاجئة في حالة النظام قيد الدراسة.

أكرر أن التحليل الذي أجرته سلسلة فورييه خطي ، في حين أن هناك عددًا كبيرًا من المرشحات غير الخطية ، لكن النظرية ليست متطورة جيدًا لأي شيء آخر غير المرشح المتوسط. مرشح كالمان هو مثال آخر على استخدام مرشح غير خطي جزئيًا ؛ الجزء غير الخطي هو "التعديل" المستقل للمرشح للإشارة.

أخيرًا ، إليك ملاحظة أساسية أخرى قمت بها عند دراسة المرشحات الرقمية. ذات يوم ، أثناء دراسة كتاب عن تكاملات فورييه ، وجدت نظرية تدعي أن اختلاف دالة مضروبة في اختلاف تحولها يجب أن يكون أكبر من ثابت معين. سألت نفسي: "ما هو إلا مبدأ عدم اليقين الشهير لميكانيكا الكم"؟ نعم ، يجب أن يكون لكل نظرية خطية مبدأ عدم اليقين يربط المتغيرات المتقاربة. بمجرد اعتماد النهج الخطي ، ويؤكد CM على الإضافة المطلقة لل eigenstates ، يجب عليك اكتشاف مبدأ عدم اليقين. يؤدي الثبات الخطي للوقت تلقائيًا إلى الوظائف الذاتية e ^ iω (t). إنها تؤدي على الفور إلى سلسلة فورييه ، ولديها بدورها مبدأ عدم اليقين.يبدو الأمر كما لو كنت ترتدي نظارات زرقاء اللون. مهما نظرت ، يجب أن يكون لونه مزرقًا!

لذلك ، أنت لست متأكدًا حقًا مما إذا كان المبدأ الشهير المتمثل في عدم اليقين CM موجود أم لا ؛ ربما يكون هذا مجرد تأثير الخطية الضمنية للنظام.

قلة من الناس يريدون أن يصدقوا أن ما نراه يعتمد على الجانب الذي نتعامل فيه مع المشكلة! في كثير من الأحيان نرى ما نريد رؤيته ، ولهذا السبب يجب عليك استخدام نهج علمي في كل مكان ، تشكك في معتقداتك الخاصة.
ولإثبات ذلك بوضوح ، سأكرر قصة إدينجتون عن الصيادين. لقد اصطادوا في الشبكة ، وعندما فحصوا حجم الأسماك التي يتم صيدها في الشبكة ، قرروا أن هناك حدًا أدنى لحجم الأسماك في البحر.

في الختام ، إذا كنت لا تشك في القواعد المعتمدة ، بين الحين والآخر ، فعلى الأرجح أنك لن تصبح قادة في أي مجال ، من ناحية أخرى ، إذا كنت تشك في كل شيء ، فسوف تكون مشلولًا ولن تفعل شيئًا . متى تتشكك ، متى تتعلم الأساسيات نفسها ، متى تفكر بنفسك ، ومتى تستمر في أخذ الأمور كما هي ، هذه مسألة أسلوب تفكير ، ولا يمكنني إعطاء صيغة بسيطة لحل هذه المشكلة. يجب أن تتعلم من تجربتك الخاصة. عادةً ما تأتي المكاسب الكبيرة بعد تغييرات كبيرة في الافتراضات الأساسية التي تستند إليها المنطقة. تحدد حالة معرفتنا التوازن بين مختلف جوانب البحث. يبدو أنه عندما تكون شابًا ، يكون لدى الحدس والبصيرة المزيد من الوقت ليؤتي ثماره ، ولكن عندما تكون كبيرًا في السن ،وقت أقل لهذا ، وربما ينبغي أن تركز على ما هو بالفعل في متناول يدك.

يتبع ...

من يريد المساعدة في ترجمة الكتاب وتخطيطه ونشره - الكتابة في بريد إلكتروني شخصي أو بريد magisterludi2016@yandex.ru

بالمناسبة ، أطلقنا أيضًا ترجمة كتاب رائع آخر - "آلة الأحلام: تاريخ ثورة الكمبيوتر" )