في هذه السلسلة من المقالات ، سوف تصبح على دراية بالمبادئ الأساسية للبرمجة الوظيفية وتفهم ما يعنيه "التفكير الوظيفي" وكيف يختلف هذا النهج عن البرمجة الشيئية أو الحتمية.

الآن بعد أن رأيت بعض الأسباب التي تجعلك تستخدم F # ، في المقالة " الغوص في F #. دليل للمطورين C # ، تراجع خطوة للخلف وناقش أساسيات البرمجة الوظيفية. ماذا تعني "البرمجة الوظيفية" حقًا ، وكيف يختلف هذا النهج عن البرمجة الشيئية أو الحتمية؟
تغيير طريقة التفكير (مقدمة)
من المهم أن نفهم أن البرمجة الوظيفية ليست مجرد نمط برمجة منفصل. هذه طريقة مختلفة تمامًا للتفكير في البرمجة ، والتي تختلف عن النهج "التقليدي" بقدر ما يختلف OOP الحالي (بأسلوب Smalltalk) عن لغة حتمية تقليدية مثل C.
F # يسمح لك باستخدام أنماط البرمجة غير الوظيفية ، وهذا يغري المبرمج للحفاظ على عاداته الحالية. يمكنك البرمجة في F # بالطريقة التي اعتدت عليها ، دون تغيير النظرة العالمية بشكل جذري ، ودون حتى معرفة ما تفتقده. ومع ذلك ، من أجل تحقيق أقصى استفادة من F # ، وأيضًا لتعلم كيفية البرمجة بثقة بأسلوب وظيفي بشكل عام ، من المهم جدًا أن تتعلم التفكير بطريقة وظيفية وليست ضرورية.
الغرض من هذه السلسلة من المقالات هو مساعدة القارئ على فهم خلفية البرمجة الوظيفية وتغيير طريقة تفكيره.
ستكون هذه سلسلة مجردة جدًا ، على الرغم من أنني سأستخدم العديد من أمثلة الرموز القصيرة لتوضيح بعض النقاط. سنتناول الموضوعات التالية:
- الدوال الرياضية . يقدم المقال الأول المفاهيم الرياضية التي تكمن وراء اللغات الوظيفية والفوائد التي يجلبها هذا النهج.
- الوظائف والقيم . يقدم ما يلي الدوال والقيم ، ويشرح كيف تختلف "القيم" عن المتغيرات ، وما هي أوجه التشابه بين الدوال والقيم البسيطة.
- أنواع . ثم ننتقل إلى الأنواع الرئيسية التي تعمل مع الوظائف: الأنواع البدائية مثل السلسلة والعدد ، ونوع الوحدة ، والأنواع الوظيفية ، والأنواع العامة.
- وظائف مع العديد من المعلمات . سأشرح كذلك مفهومي "الكاري" و "التطبيق الجزئي". في هذا المكان ، سيؤذي دماغ شخص ما ، خاصة إذا كان لهذه العقول ماض حتمي فقط.
- تعريف الوظائف . ثم سيتم تخصيص العديد من الوظائف للعديد من الطرق المختلفة لتحديد ودمج الوظائف.
- توقيعات الدوال . ما يلي هو منشور مهم عن القيمة الحرجة لتوقيعات الوظائف ، وما تعنيه ، وكيفية استخدام التوقيعات لفهم محتويات الوظائف.
- تنظيم الوظائف . عندما يصبح من الواضح كيفية إنشاء الوظائف ، يبرز السؤال: كيف يمكنك تنظيمها لجعلها في متناول بقية الشفرة؟
وظائف الرياضيات
البرمجة الوظيفية مستوحاة من الرياضيات. تحتوي الدوال الرياضية على عدد من الميزات الرائعة جدًا التي تحاول اللغات الوظيفية تنفيذها.
لنبدأ بوظيفة الرياضيات التي تضيف 1 إلى رقم.
Add1(x) = x+1
ماذا يعني هذا التعبير حقا؟ يبدو بسيطا جدا. هذا يعني أن هناك مثل هذه العملية التي تأخذ رقمًا وتضيف 1 إليه.
أضف بعض المصطلحات:
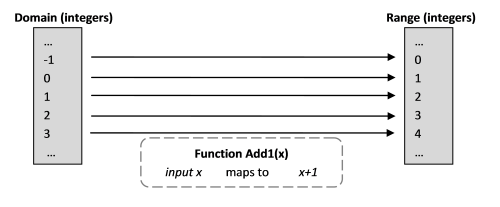
- تسمى مجموعة قيم دالة الإدخال الصالحة المجال (النطاق). في هذا المثال ، يمكن أن يكون هناك الكثير من الأرقام الحقيقية ، لكننا سنجعل الحياة أبسط ونقتصر هنا على الأعداد الصحيحة.
- مجموعة النتائج المحتملة للوظيفة (نطاق القيم) تسمى النطاق (تقنيًا ، صورة كودوم ). في هذه الحالة ، هناك أيضًا العديد من الأعداد الصحيحة.
- تسمى الوظيفة تعيين (في الخريطة الأصلية) من مجال إلى نطاق. (أي من النطاق إلى النطاق.)
هكذا سيبدو هذا التعريف في F #.
let add1 x = x + 1
إذا قمت بإدخالها في F # Interactive (لا تنسى الفواصل المنقوطة المزدوجة) ، فيمكنك رؤية النتيجة ("توقيع" الوظيفة):
val add1 : int -> int
النظر في الاستنتاج بالتفصيل:
- المعنى العام هو أن وظيفة
add1 تقارن الأعداد الصحيحة (من مجال التعريف) بالأعداد الصحيحة (من نطاق القيم). - يتم تعريف "
add1 " على أنه "val" ، وهو اختصار لـ "value". همم؟ ماذا تعني سنناقش المعاني بعد قليل. - يُستخدم رمز السهم "->" لإظهار المجال والنطاق. في هذه الحالة ، يكون المجال من النوع 'int' ، مثل النطاق.
لاحظ أن النوع لم يتم تحديده بشكل صريح ، لكن المترجم F # قرر أن الوظيفة تعمل مع الدرجات. (هل يمكن تغيير هذا؟ نعم ، وقريبا سنراه).
الخصائص الرئيسية للوظائف الرياضية
تحتوي الدوال الرياضية على عدد من الخصائص التي تميزها كثيرًا عن الدوال المستخدمة في البرمجة الإجرائية.
- للوظيفة دائمًا نفس النتيجة لنفس قيمة الإدخال.
- الوظيفة ليس لها آثار جانبية.
توفر هذه الخصائص عددًا من المزايا البارزة التي تحاول لغات البرمجة الوظيفية تحقيقها قدر الإمكان في تصميمها. سننظر في كل واحد منهم بدوره.
ترجع الدوال الرياضية دائمًا نفس النتيجة إلى قيمة معينة
في البرمجة الحتمية ، نعتقد أن الوظائف إما "تفعل" شيئًا أو "تحسب" شيئًا. لا تحسب وظائف الرياضيات أي شيء ، إنها تعيينات خالصة من الإدخال إلى الإخراج. في الواقع ، تعريف آخر للدالة هو مجموعة بسيطة من جميع التعيينات. على سبيل المثال ، يمكنك تحديد الوظيفة "add1" (في C #) بشكل فظ جدًا
int add1(int input) { switch (input) { case 0: return 1; case 1: return 2; case 2: return 3; case 3: return 4; etc ad infinitum } }
من الواضح أنه من المستحيل وجود قضية لكل رقم ممكن ، ولكن المبدأ هو نفسه. باستخدام هذا الإعداد ، لا يتم إجراء أي حسابات ، يتم إجراء بحث فقط.
وظائف الرياضيات خالية من الآثار الجانبية
في دالة رياضية ، تكون قيم المدخلات والمخرجات شيئين مختلفين منطقيًا ، كلاهما محددان مسبقًا. لا تغير الوظيفة بيانات الإدخال أو الإخراج ، وتقوم ببساطة بتعيين قيمة الإدخال المحددة مسبقًا من منطقة التعريف إلى قيمة الإخراج المحددة مسبقًا في منطقة القيمة.
بمعنى آخر ، لا يمكن أن يكون لحساب الوظيفة أي تأثيرات على بيانات الإدخال أو أي شيء آخر من هذا النوع . يجب أن نتذكر أن حساب دالة لا يحسب أو يتلاعب بأي شيء ، إنه مجرد بحث مبالغ فيه.
هذا "الثبات" للقيم خفي للغاية ، ولكن في الوقت نفسه شيء مهم للغاية. عندما أقوم بالرياضيات ، لا أتوقع أن تتغير الأرقام عند إضافتها. على سبيل المثال ، إذا كان لدي:
x = 5 y = x+1
لا أتوقع x تتغير x عندما أضيف 1. أتوقع الحصول على رقم مختلف ( y ) ، ويجب أن يظل x حاله. في عالم الرياضيات ، توجد الأعداد الصحيحة بالفعل في مجموعة ثابتة ، ووظيفة add1 تحدد ببساطة العلاقة بينهما.
قوة الوظيفة النقية
تسمى هذه الأنواع من الوظائف التي لها نتائج قابلة للتكرار وليس لها آثار جانبية "وظائف نقية" ، ويمكنك القيام ببعض الأشياء المثيرة للاهتمام معها:
- من السهل موازنتها. لنفترض أننا يمكن أن نأخذ أعدادًا صحيحة في النطاق من 1 إلى 1000 وتوزيعها على 1000 معالج مختلف ، وبعد ذلك نوجه كل وحدة معالجة مركزية لتنفيذ "
add1 " على الرقم المقابل ، مع التأكد من عدم وجود حاجة لأي تفاعل بينهما. لا أقفال ولا كائنات ولا إشارات ، إلخ. - يمكنك استخدام الوظائف بشكل كسول ، وحسابها عند الضرورة لمنطق البرنامج. يمكنك التأكد من أن الإجابة ستكون هي نفسها تمامًا ، بغض النظر عما إذا كانت الحسابات تتم الآن أو لاحقًا.
- يمكنك فقط إجراء حسابات دالة لمدخل معين ، ثم تخزين النتيجة مؤقتًا ، لأنه من المعروف أن قيم الإدخال هذه ستعطي نفس المخرجات.
- إذا كان هناك العديد من الوظائف النقية ، فيمكن حسابها بأي ترتيب. مرة أخرى ، هذا لا يمكن أن يؤثر على النتيجة النهائية.
وفقًا لذلك ، إذا كان من الممكن إنشاء وظائف نقية بلغة برمجة ، يمكنك على الفور تلقي العديد من الحيل القوية. ولا شك أن كل هذا يمكن القيام به في F #:
- مثال على الحوسبة المتوازية كان في سلسلة "لماذا استخدام F #؟" .
- سيتم مناقشة حساب الدالة البطيئة في سلسلة التحسين .
- تسمى نتائج وظيفة التخزين المؤقت بالمحاكاة وسيتم مناقشتها أيضًا في سلسلة التحسين .
- إن غياب الحاجة إلى تتبع أمر التنفيذ يجعل البرمجة المتوازية أسهل بكثير ويلغي الحاجة إلى الأخطاء الناتجة عن تغيير ترتيب الوظائف أو إعادة البناء.
خصائص "عديمة الفائدة" للوظائف الرياضية
تحتوي الدوال الرياضية أيضًا على بعض الخصائص التي تبدو غير مفيدة جدًا عند البرمجة.
- قيم المدخلات والمخرجات ثابتة
- للوظائف دائمًا إدخال واحد وإخراج واحد.
تنعكس هذه الخصائص في تصميم لغات البرمجة الوظيفية. يجدر النظر فيها بشكل منفصل.
قيم المدخلات والمخرجات ثابتة
تبدو القيم الثابتة من الناحية النظرية فكرة جيدة ، ولكن كيف يمكن القيام بأي عمل حقًا إذا لم تكن هناك طريقة لتعيين متغير بالطريقة التقليدية.
يمكنني أن أؤكد لكم أن هذه ليست مشكلة كبيرة كما تتصورون. في هذه السلسلة من المقالات ، سيكون من الواضح كيف يعمل ذلك عمليًا.
تحتوي الدوال الرياضية دائمًا على إدخال واحد وإخراج واحد.
كما يتبين من الرسوم البيانية ، للدالة الرياضية ، يوجد دائمًا مدخل واحد ومخرج واحد فقط. ينطبق هذا أيضًا على لغات البرمجة الوظيفية ، على الرغم من أنه قد لا يكون واضحًا عند استخدامه لأول مرة.
يبدو هذا إزعاجًا كبيرًا. كيف يمكنني القيام بشيء مفيد بدون وظائف مع معلمتين (أو أكثر)؟
اتضح أن هناك طريقة للقيام بذلك ، والأكثر من ذلك أنها شفافة تمامًا على F #. يطلق عليه "الكاري" ، ويستحق مشاركة منفصلة ، والتي ستظهر في المستقبل القريب.
في الواقع ، سيتضح لاحقًا أن هاتين الخاصيتين "عديمة الفائدة" ستصبح ذات قيمة لا تصدق ، وستكون الجزء الرئيسي الذي يجعل البرمجة الوظيفية قوية جدًا.
موارد إضافية
هناك العديد من البرامج التعليمية لـ F # ، بما في ذلك المواد لأولئك الذين يأتون مع تجربة C # أو Java. قد تكون الروابط التالية مفيدة عندما تتعمق في F #:
كما تم وصف عدة طرق أخرى لبدء تعلم F # .
أخيرًا ، مجتمع F # ودود للغاية للمبتدئين. هناك محادثة نشطة للغاية في Slack ، تدعمها F # Software Foundation ، مع غرف للمبتدئين يمكنك الانضمام إليها بحرية . نوصي بشدة أن تفعل ذلك!
لا تنس زيارة موقع المجتمع الناطق باللغة الروسية F # ! إذا كان لديك أي أسئلة حول تعلم لغة ، يسعدنا مناقشتها في غرف الدردشة:
حول مؤلفي الترجمة
ترجمه kleidemos
 تم إجراء تغييرات الترجمة والتحرير من خلال جهود المجتمع الناطق باللغة الروسية لمطوري F # . نشكر أيضًا schvepsss و shwars لإعداد هذه المقالة للنشر.
تم إجراء تغييرات الترجمة والتحرير من خلال جهود المجتمع الناطق باللغة الروسية لمطوري F # . نشكر أيضًا schvepsss و shwars لإعداد هذه المقالة للنشر.