⏳ 🚪 🕣 ديناميات الطيران العمودي للطائرة أخف من الهواء 👨‍👨‍👧‍👧 🤦 👶🏿

مقدمة

إن تحديد سرعة صعود وهبوط الطائرات أخف من الهواء (LALV) حتى الآن يكاد يكون مهمة مهمة تنشأ في تصميم هذه الأجهزة.

تم تخصيص عدد كبير من المنشورات لـ LALF ، على سبيل المثال ، فقط على مواردنا مقالتان مثيرتان للاهتمام للغاية [1،2] تتعلق بتاريخ التطوير على مثال تصميمات محددة للمناطيد والستراتوستات. ومع ذلك ، هناك عدد قليل جدًا من حسابات ديناميكيات الطيران العمودي لهذه الأجهزة ، مما يسمح على الأقل بتحديد سرعة الصعود والنزول للأسلحة الصغيرة والأسلحة الخفيفة.

يتطلب البيان الأخير شرحًا معينًا ، حيث يتذكر القارئ ذو الخبرة مسار الفيزياء المدرسية ، حيث تم حل المشاكل المتعلقة بارتفاع الارتفاع والمعلمات الأخرى للبالونات المملوءة بغازات أخف من الهواء أو عن طريق الهواء نفسه الذي يتم تسخينه أثناء الرحلة.

استندت جميع هذه المهام على المساواة بين قوتين: قوة الوزن وقوة الطفو. اعتبرت الغازات مثالية وتم حساب معلماتها وفقًا لقانون Mendeleev Clapeyron. ومع ذلك ، حتى الحساب البسيط للقوة الثالثة لمقاومة الهواء يؤدي بالفعل إلى نظام من المعادلات التفاضلية ، والتي لا يمكن حلها بشكل تحليلي. من الضروري أيضًا مراعاة التغير في كثافة الهواء الجوي مع ارتفاع الارتفاع ودرجة الحرارة.

بالإضافة إلى ذلك ، إذا كنت بحاجة إلى النظر ليس فقط في الارتفاع ، ولكن أيضًا في تجميد الكرة وهبوطها على الأرض ، فهي ليست مهمة للأطفال على الإطلاق. آمل ألا يسهم النظر في حل مشكلة مماثلة عن طريق بايثون في توسيع المعرفة في الفيزياء فحسب ، بل أيضًا تعميم لغة البرمجة بيثون نفسها. ما أحاول القيام به في منشوري على هذا المورد.

نموذج رياضي لرحلة LALV مع قذيفة على شكل كرة ، لا يتغير حجمها مع الارتفاع

نحن نقصر أنفسنا على النظر في حركة مركز كتلته تحت تأثير القوى التالية: الجاذبية ( G ) ، قوة Archimedean ( Fa ) وقوة السحب الهوائية ( Fc ). نكتب العلاقات لتحديد القوى من خلال بارامترات الحركة والبيئة الجوية [3]:

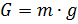
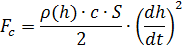
في الصيغ أعلاه ، يتم استخدام الترميز: h هو ارتفاع الكرة ، dh / dt هو السرعة الرأسية ، m هي الكتلة ، g هو تسارع الجاذبية ، W هو حجم الكرة ، c هو معامل السحب ، S هي منطقة المقاومة المميزة (منطقة ميدسيب).
يفترض أن اعتماد كثافة الهواء على الارتفاع سيكون أسيًا:

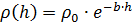
أين

ρ_{0}

$ρ_0$ - كثافة الهواء عند ارتفاع صفر ، ب - معامل. يتم توجيه قوة الجاذبية إلى أسفل ، يتم توجيه قوة Archimedean إلى أعلى ، وقوة السحب الديناميكي الهوائية يتم توجيهها دائمًا "ضد الحركة" ، وبالتالي ، فإن الإدراج الصحيح لهذه القوة في معادلات الحركة يتطلب إدخال عامل

- s i n g (d h / d t)

$-sing (dh / dt)$ .

ومع ذلك ، لأغراضنا ، هذه الحقيقة ليست ذات أهمية أساسية ، ونقتصر على النظر فقط في مرحلة رفع الكرة ، عندما يتم توجيه قوة السحب الهوائية إلى الأسفل ، وبالتالي ، سيتم أخذها في الاعتبار في معادلات الحركة مع علامة ناقص. الآن يمكن كتابة معادلة الحركة على النحو التالي:

، (1)

بالإضافة إلى ذلك ، افترض أن البالون عبارة عن جسم متجانس نصف قطره R بكثافة

ρ_{b}

$ρ_b$ . ثم يتم تحديد حجم المنطقة التي تحدد سحبها الديناميكي الهوائي على أنه

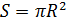
حجم باسم

، والكتلة ، على التوالي ، كما

.

من الواضح الآن أن كل حد من المعادلة (1) يحتوي على S. كعامل ، وبالتالي ، يمكن تقليل كل حد من معادلة الحركة بعامل S. ستأخذ المعادلة نفسها الشكل:

، (2)

نقدم الترميز التالي:

؛

وإعادة كتابة (2) في شكل النظام التالي من المعادلات غير الخطية:

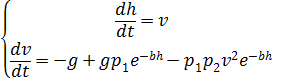
، (3)

التأثير على سرعة وارتفاع ارتفاع درجة حرارة الهواء LALV

للقيام بذلك ، نقوم أولاً بحل النظام (3) باستخدام العلاقة التالية لاعتماد كثافة الهواء الجوي على الارتفاع دون مراعاة درجة الحرارة:

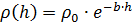
دعونا نكرر حل النظام (3) ، ولكن باستخدام العلاقة لاعتماد كثافة الهواء على الارتفاع ودرجة الحرارة:

حيث: b = 0.000125 هو ثابت مرتبط بكثافة هواء 1 / م ؛
a = 0.0065 هو ثابت متعلق بدرجة حرارة الهواء بـ K / m.

$inline$ - درجة حرارة سطح البحر.

قائمة البرنامج

# -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. R=8#     . b=0.000125# ,      1/ a=6.5*10**-3# ,      / c=0.4#   mo=240#   V=(4/3)*pi*R**3 rs=rg+mo/V#    ,  ,   p1=rv/rs#   p2=3*c/(8*R)#   T0=300 def fun(y, t): y1, y2= y return [y2,-g+g*p1*exp(-b*y1*T0/(T0-a*y1))-p1*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] t =arange(0,1100,0.01) y0 = [0.0,0.0] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.title("   \n : %s 3.  : %s . \n  : %s k. "%(round(V,0),mo,round(0.001*g*rv*V,0))) plt.plot(t/60,y1,label='  : %s . \n  : % s / .\n    '%(round(max(y1)/1000,2),round(max(y2),2))) def fun(y, t): y1, y2= y return [y2,-g+g*p1*exp(-b*y1)-p1*p2*exp(-b*y1)*y2**2] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.plot(t/60,y1,label='  : %s . \n  : % s / \n    '%(round(max(y1)/1000,2),round(max(y2),2))) plt.ylabel('  ') plt.xlabel('   ') plt.legend(loc='best') plt.grid(True) plt.show()

نحصل على:

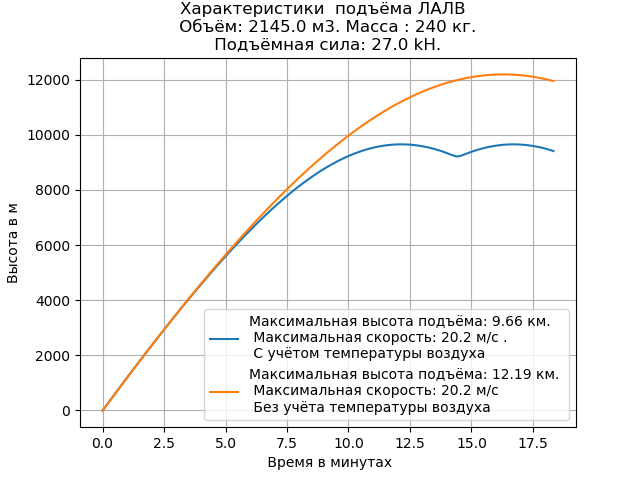
القيمة المحسوبة لارتفاع المصعد LALV ، مع مراعاة درجة الحرارة ، أقل من بدونها. لا تزال سرعة رفع الجهاز دون تغيير.

تحديد خصائص جميع مراحل رحلة SALV من البداية إلى الهبوط

لبناء برنامج الرحلة LALV النظر في شروط الفترات الزمنية التالية:

صعود -

؛
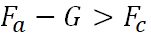
تعليق -

؛
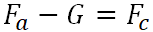
الهبوط -

قائمة البرنامج

 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. R=8#     . b=0.000125# ,      1/ a=6.5*10**-3# ,      / c=0.4#    mo=240#    V=(4/3)*pi*R**3 p2=3*c/(8*R)#   T0=300#     tz=4000#     rgu=1.2#         /3 tz=4000#   def fun(y, t): y1,y2= y if y2<=0: if t<tz: return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] elif t>=tz: return [y2,-g+g*(rv/(rgu+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rgu+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] else: return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))-(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] t =arange(0,tz+555,0.1) y0 = [0.0,0.0] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.title(", ,   \n      \n : %s 3.  : %s .  : %s k. "%(round(V,0),mo,round(0.001*g*rv*V,0))) plt.plot(t,y1,label='  : %s . \n  : % s / .\n   %s .'%(round(max(y1)/1000,2), round(max(y2),2),tz-2*555)) plt.ylabel('  ') plt.xlabel('   .') plt.legend(loc='best') plt.grid(True) plt.show()

نحصل على:

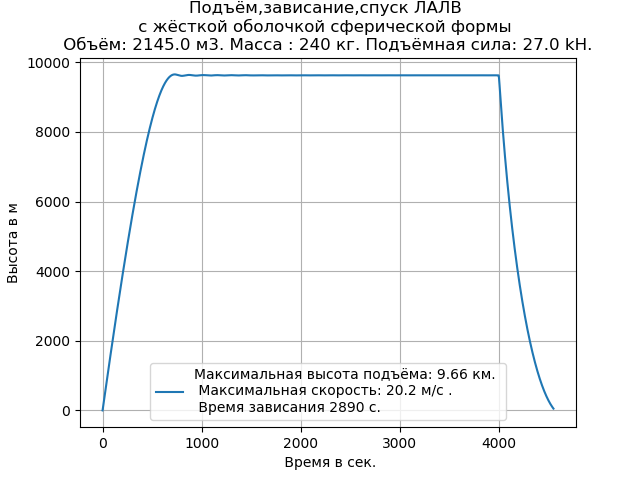
على النحو التالي من الرسم البياني وقائمة البرنامج ، لإجراء تجربة حسابية ، يكفي إدخال البيانات الأولية اللازمة.

نموذج رياضي لرحلة LALV مع قذيفة ، يختلف حجمها مع الارتفاع

مثل LALV تشمل ستراتوستاتس. لا يمكن نفخ بالون الستراتوسفير بشكل كامل بالهيليوم ، مما يمنحه أقصى قوة رفع ، والتي ستحول شكل قشرته إلى كرة. يمكن أن تنفجر مثل هذه الكرة على ارتفاع عالٍ بسبب الاختلاف المتزايد في الضغوط الداخلية والخارجية.

لهذه الأسباب ، لحساب الحد الأقصى لارتفاع الرفع الممكن تحقيقه ، يتم إدخال قيمتين لحجمه: الحد الأدنى Vmin والحد الأقصى Vmax ، على التوالي. مع الأخذ في الاعتبار المتغيرات المقدمة واعتماد كثافة الهواء على الارتفاع ، فإن نسب قوة الطفو Fa وقوة الجاذبية: تأخذ الشكل التالي:

، (4)

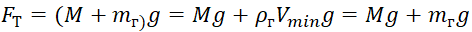
، (5)

حيث: M هي كتلة القشرة والمعدات في الستراتوستات ؛

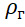
هي كثافة الهيليوم.

العلاقات المتساوية (4) و (5) ، على افتراض أن حجم القشرة V هو دالة لارتفاع LALV ، نحصل على النسبة:

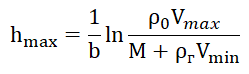
. (6)

يتم إعطاء القيم العددية للمعلمات المدرجة في العلاقة (6) في القائمة لإنشاء رسم بياني ، يتم تقديمه فقط للغرض المشار إليه.

إدراج مخطط بالبيانات

 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. Vmin=400#    /3. b=0.000128# ,      1/. c=0.8#   mo=40#   rs=rg+mo/Vmin#    ,     p1=rv/rs#   h=[(10**-3)*log((rv*w)/(mo+rg*Vmin))*b**-1 for w in arange(1*10**3,1.8*10**5,1000)] v=[(10**-3)*w for w in arange(1*10**3,1.8*10**5,1000)] plt.title("     \n    ") plt.plot(v,h) plt.xlabel('    . 3') plt.ylabel('     .') plt.grid(True) plt.show()

نحصل على:

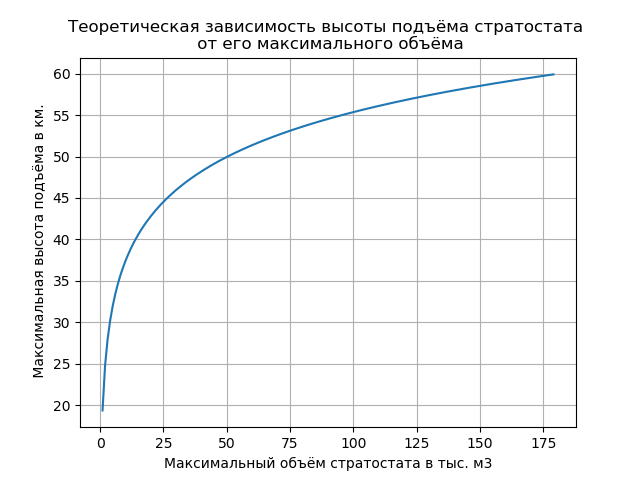
من خلال تغيير معلمات LALV المدرجة في قائمة البرنامج ، يمكنك الحصول على الرسم البياني المحدد وتحديد الحد الأقصى لحجم الغلاف المطلوب أثناء التصميم. يتم تنقيح النتائج باستخدام خبرة واسعة في إنشاء مثل هذه الأجهزة.

الاستنتاجات:

يتم الحصول على نماذج رياضية لنوعين من الطائرات أخف من الهواء ، مما يسمح بالتجارب الحسابية لتقييم معلمات هذه الأجهزة في الظروف المثالية لبيئة الهواء.
يسمح المخطط المقترح متعدد المراحل للحل العددي لنظام المعادلات التفاضلية للمرء بالحصول على المسار العمودي للطائرة أخف من الهواء في مراحل صعود التحليق والنزول.

المراجع

بضع كلمات حول المناطيد
في الطريق الى الفضاء. ستراتوستاتس
ريجيكوف يو. فورتران الحديثة. - سانت بطرسبرغ: طباعة كراون 2004 - 288 ص.

ديناميات الطيران العمودي للطائرة أخف من الهواء

مقدمة

نموذج رياضي لرحلة LALV مع قذيفة على شكل كرة ، لا يتغير حجمها مع الارتفاع

التأثير على سرعة وارتفاع ارتفاع درجة حرارة الهواء LALV

تحديد خصائص جميع مراحل رحلة SALV من البداية إلى الهبوط

نموذج رياضي لرحلة LALV مع قذيفة ، يختلف حجمها مع الارتفاع

المراجع

More articles: