 تستند نظرية الأوتار على فكرة أنه بدلاً من الجسيمات الأولية ذات الأبعاد الصفرية ، يتكون الكون من سلاسل أحادية البعد
تستند نظرية الأوتار على فكرة أنه بدلاً من الجسيمات الأولية ذات الأبعاد الصفرية ، يتكون الكون من سلاسل أحادية البعدنظرية الأوتار هي واحدة من أكثر أفكار الفيزياء اللامعة والمتناقضة وغير المثبتة. إنه يقوم على اتجاه مادي عاش لعدة قرون - على مستوى أساسي ما ، ترتبط جميع القوى المختلفة والجسيمات والتفاعلات ومظاهر الواقع معًا كأجزاء مختلفة من منصة واحدة. بدلاً من أربعة تفاعلات أساسية مستقلة - قوية ، كهرومغناطيسية ، ضعيفة وجاذبية - هناك نظرية واحدة موحدة تحتضنهم جميعًا.
من نواح عديدة ، تعتبر نظرية الأوتار هي أفضل مرشح لنظرية الكم للجاذبية ، حيث تجمع بين التفاعلات على أعلى مستويات الطاقة. على الرغم من عدم وجود دليل تجريبي على ذلك ، هناك أسباب نظرية مقنعة للاعتقاد أن هذا هو الحال. في عام 2015 ، كتب أكبر متخصص في نظرية الأوتار الحية ، إدوارد ويتن ،
ورقة حول ما يجب أن يعرفه كل فيزيائي حول نظرية الأوتار. وهذا ما يعنيه - حتى لو لم تكن فيزيائيًا.
 الفرق بين التفاعلات المعيارية لنظرية المجال الكمي (يسار) للجسيمات النقطية والتفاعلات في نظرية الأوتار (يمين) للسلاسل المغلقة.
الفرق بين التفاعلات المعيارية لنظرية المجال الكمي (يسار) للجسيمات النقطية والتفاعلات في نظرية الأوتار (يمين) للسلاسل المغلقة.من المثير للدهشة أنه في بعض الأحيان توجد الكثير من أوجه التشابه في قوانين الطبيعة المتعلقة بظواهر تبدو غير ذات صلة. غالبًا ما تكون الهياكل الرياضية لمثل هذه الظواهر متشابهة جدًا ، وأحيانًا متطابقة. إن جاذبية جسدين ضخمين وفقًا لقوانين نيوتن مماثل تقريبًا لجذب / تنافر الجسيمات المشحونة كهربائيًا. تتشابه تذبذبات البندول تمامًا مع حركة الكتلة في الربيع أو الكوكب حول النجم. أمواج الجاذبية ، أمواج الماء ، أمواج الضوء - كلها لها خصائص مشابهة بشكل مدهش ، على الرغم من حقيقة أنها تأتي من مصادر مادية مختلفة جوهريًا. وعلى نفس المنوال ، على الرغم من أن الكثيرين لا يدركون ذلك ، فإن النظرية الكمية لجسيم واحد ونهج نظرية الجاذبية الكمومية متشابهتان أيضًا.
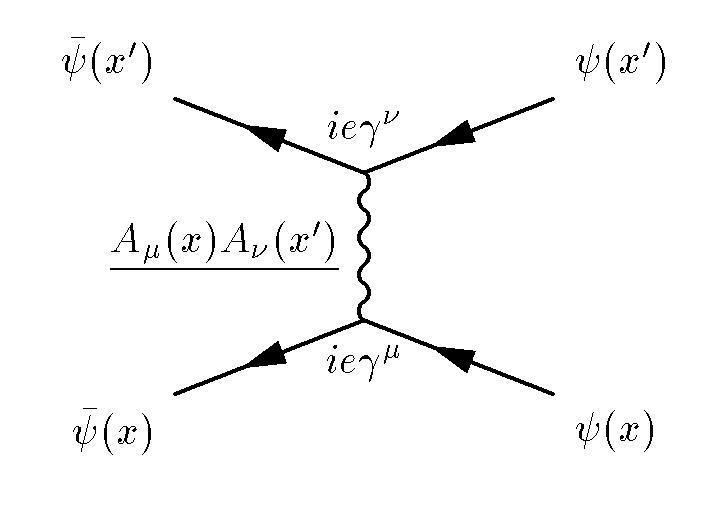 مخطط فاينمان يمثل تشتت إلكترونين - لهذا من الضروري تلخيص جميع التواريخ الممكنة لتفاعلات الجسيمات
مخطط فاينمان يمثل تشتت إلكترونين - لهذا من الضروري تلخيص جميع التواريخ الممكنة لتفاعلات الجسيماتتعمل نظرية المجال الكمي على النحو التالي: خذ جزيئًا وأجري "تجميعًا لجميع قصصه" الرياضية. لا يمكنك فقط حساب مكان الجسيم ، وأين هو الآن ، وكيف وصل إلى هناك - لأنه في الطبيعة يوجد عدم اليقين الكمي الداخلي والأساسي. بدلاً من ذلك ، نلخص كل الطرق الممكنة التي يمكن أن تصل بها إلى الحالة الحالية ("التاريخ الماضي") ، مع الأوزان الاحتمالية المقابلة ، ثم نحسب الحالة الكمية لجسيم واحد.
للعمل مع الجاذبية ، وليس مع الجسيمات الكمية ، تحتاج إلى التغيير قليلاً. بما أن نظرية النسبية العامة لأينشتاين لا ترتبط بالجسيمات ، ولكن مع انحناء الزمكان ، فلن نحسب جميع تواريخ الجسيمات الممكنة. وبدلاً من ذلك ، فإننا نحسب جميع الأشكال الهندسية للمكان.
 الجاذبية وفقًا لقواعد آينشتاين وكل شيء آخر (التفاعلات القوية والضعيفة والكهرومغناطيسية) وفقًا لقواعد فيزياء الكم هي مجموعتان مختلفتان من القوانين التي تحكم كل شيء في الكون.
الجاذبية وفقًا لقواعد آينشتاين وكل شيء آخر (التفاعلات القوية والضعيفة والكهرومغناطيسية) وفقًا لقواعد فيزياء الكم هي مجموعتان مختلفتان من القوانين التي تحكم كل شيء في الكون.من الصعب جدًا العمل في ثلاثة أبعاد مكانية ، وعندما نواجه مشكلة جسدية معقدة ، غالبًا ما نحاول حل نسخة أبسط لها أولاً. إذا ذهبت بعدًا واحدًا ، فسيصبح كل شيء أسهل. الأسطح الوحيدة ذات البعد الواحد هي سلسلة مفتوحة ، مع نهايتين منفصلتين غير متصلتين ببعضهما البعض ، أو سلسلة مغلقة ، ترتبط نهاياتها وتشكل حلقة. بالإضافة إلى ذلك ، يصبح انحناء الفضاء - المعقد للغاية في ثلاثة أبعاد - مسألة تافهة. لذلك ، إذا أردنا إضافة مادة ، فإننا نستخدم مجموعة من الحقول العددية (تمامًا مثل نوع معين من الجسيمات) وثابت كوني (يعمل تمامًا كعضو في المعادلة المسؤولة عن الكتلة): تشبيه كبير.
إن درجات الحرية الإضافية التي يحصل عليها الجسيم في عدة أبعاد لا تلعب دورًا خاصًا ؛ طالما يمكننا تحديد متجه الزخم ، يبقى هذا البعد الرئيسي. لذلك ، في أحد الأبعاد ، تبدو الجاذبية الكمية تمامًا مثل الجسيمات الكمومية الحرة في أي عدد عشوائي من الأبعاد.
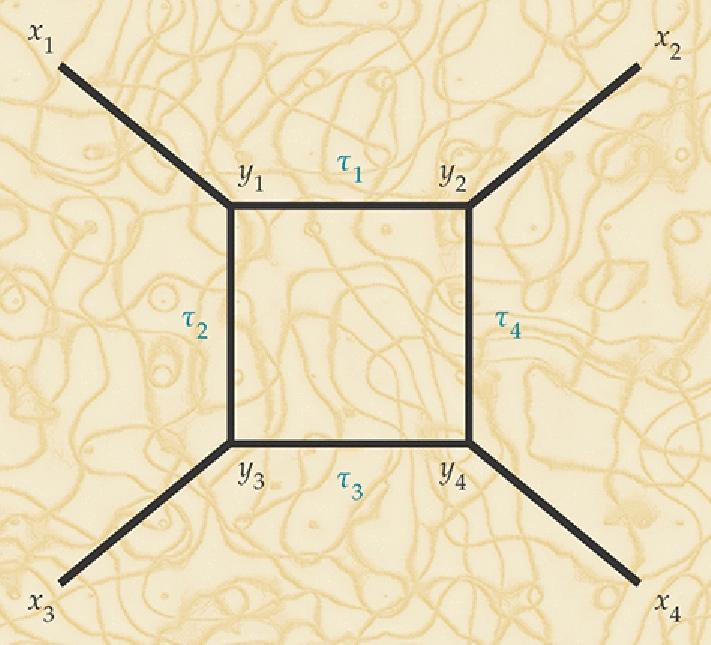 رسم بياني به قمم حيث تتلاقى ثلاث حواف هو مكون رئيسي لبناء المسار المتكامل المتعلق بالجاذبية الكمية أحادية البعد
رسم بياني به قمم حيث تتلاقى ثلاث حواف هو مكون رئيسي لبناء المسار المتكامل المتعلق بالجاذبية الكمية أحادية البعدالخطوة التالية هي تشغيل التفاعلات ، والانتقال من جسيم حر دون
تناثر السعات أو
المقاطع العرضية الفعالة إلى جزء قد يكون له دور مادي مرتبط بالكون. تسمح لنا الرسوم البيانية المشابهة للرسم أعلاه بوصف المفهوم المادي للعمل في الجاذبية الكمية. إذا كتبنا جميع المجموعات الممكنة من هذه الرسوم البيانية وقمنا بتلخيصها - باستخدام نفس القوانين كالمعتاد ، على سبيل المثال ، قانون الحفاظ على الزخم - يمكننا إكمال القياس. الجاذبية الكمومية في بعد واحد تشبه إلى حد كبير تفاعل جسيم واحد في أي عدد من الأبعاد.
 إن احتمال الكشف عن جسيم كمي في مكان معين لا يكون 100 ٪ أبدًا ؛ الاحتمالية موزعة على المكان والزمان.
إن احتمال الكشف عن جسيم كمي في مكان معين لا يكون 100 ٪ أبدًا ؛ الاحتمالية موزعة على المكان والزمان.الخطوة التالية هي الانتقال من بعد مكاني واحد إلى أبعاد 3 + 1: إلى حيث يكون للكون ثلاثة أبعاد مكانية وواحدة زمنية. لكن هذه "الترقية" النظرية للجاذبية يمكن أن تكون صعبة للغاية. يمكن العثور على نهج مختلف إذا قررنا العمل في الاتجاه المعاكس.
بدلاً من حساب سلوك جسيم واحد (كيان بدون أبعاد) في أي عدد من الأبعاد ، ربما يمكننا حساب سلوك سلسلة ، مفتوحة أو مغلقة (كيان أحادي البعد). وعلى هذا الأساس ، ابحث بالفعل عن تشابهات لنظرية أكثر اكتمالاً للجاذبية الكمية في عدد أكثر واقعية من الأبعاد.
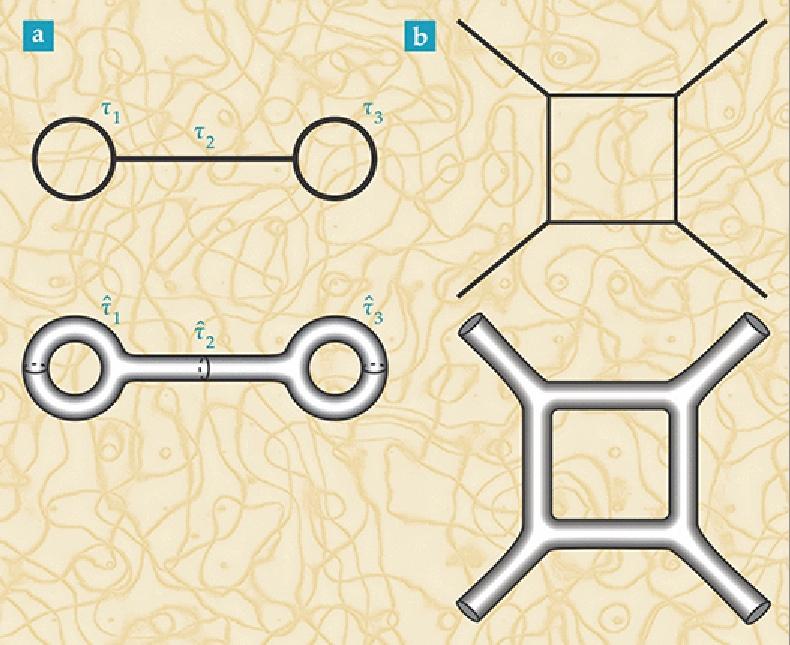 تستند مخططات Feynman (أعلاه) على الجسيمات النقطية وتفاعلاتها. بتحويلها إلى نظائرها لنظرية الأوتار (أدناه) ، نحصل على أسطح يمكن أن يكون لها انحناء غير تافه.
تستند مخططات Feynman (أعلاه) على الجسيمات النقطية وتفاعلاتها. بتحويلها إلى نظائرها لنظرية الأوتار (أدناه) ، نحصل على أسطح يمكن أن يكون لها انحناء غير تافه.بدلاً من النقاط والتفاعلات ، نبدأ فورًا في العمل مع الأسطح والأغشية وما إلى ذلك. بعد الحصول على سطح متعدد الأبعاد حقيقي ، يمكننا ثنيه بطرق غير تافهة. نبدأ في مراقبة سلوكها المثير للاهتمام للغاية. واحدة يمكن أن تكون أساس انحناء الزمكان الملاحظ في الكون في إطار الموارد الوراثية.
ولكن على الرغم من أن الجاذبية الكمية أحادية البعد تعطينا نظرية المجال الكمي للجسيمات في الزمكان المنحني المحتمل ، إلا أنها وحدها لا تصف الجاذبية. ما هو مفقود في هذا اللغز؟ لا يوجد تطابق بين العوامل أو الوظائف التي تمثل التفاعلات والخصائص الميكانيكية الكمومية ، وكذلك الحالات ، أي كيف تتغير الجسيمات وخصائصها بمرور الوقت. كانت مراسلات "مشغلي الدولة" هذه عنصرًا ضروريًا ولكنه مفقود.
ولكن إذا انتقلنا من الجسيمات النقطية إلى الكيانات الوترية ، فإن هذه المراسلات تتجلى.
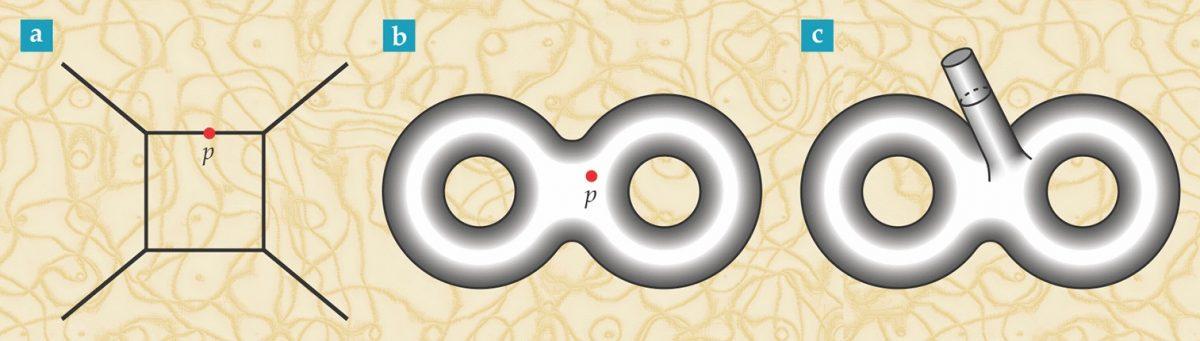 يمكن تمثيل تشوه مقياس الزمكان بتقلب ('p') ، وإذا تم تطبيقه على تشبيه السلسلة ، فسوف يصف تقلب الزمكان ويتوافق مع الحالة الكمية للسلسلة.
يمكن تمثيل تشوه مقياس الزمكان بتقلب ('p') ، وإذا تم تطبيقه على تشبيه السلسلة ، فسوف يصف تقلب الزمكان ويتوافق مع الحالة الكمية للسلسلة.في الانتقال من الجسيمات إلى السلاسل ، تظهر مراسلات حقيقية بين حالات التشغيل. يمثل التقلب في مقياس الزمكان (أي العامل) تلقائيًا الحالة في الوصف الميكانيكي الكمومي لخصائص السلسلة. لذلك ، يمكن إنشاء نظرية الكم للجاذبية في الزمكان على أساس نظرية الأوتار.
لكن هذا ليس كل ما نحصل عليه: نحصل أيضًا على الجاذبية الكمية ، جنبًا إلى جنب مع الجسيمات والتفاعلات الأخرى في الزمكان ، مع تلك التي تتوافق مع عوامل الأوتار الأخرى في نظرية المجال. هناك أيضًا عامل يصف التقلبات في هندسة الزمكان ، وآخر عامل للحالات الكمومية للسلسلة. الشيء الأكثر إثارة للاهتمام حول نظرية الأوتار هو أنها يمكن أن تعطينا نظرية كمية جاذبية عاملة.
 يقدم Brian Green عرضًا حول نظرية الأوتار
يقدم Brian Green عرضًا حول نظرية الأوتاركل هذا لا يعني أن المشكلة قد تم حلها ، وأن نظرية الأوتار هي الطريق إلى الجاذبية الكمية. إن الأمل الكبير لنظرية الأوتار هو أنه يمكن الحفاظ على هذه المقارنات على جميع المستويات ، وأنه سيكون هناك مراسلات لا لبس فيها من شخص لآخر للصورة الوترية للعالم والكون التي نلاحظها حولنا.
حتى الآن ، فإن صورة العالم بأوتار وخيوط متناسقة في مجموعات قليلة فقط من الأبعاد ، وأكثرها واعدة لا تعطينا جاذبية أينشتاين رباعية الأبعاد ، التي تصف كوننا. بدلاً من ذلك ، نكتشف
نظرية الجاذبية 10-الأبعاد
بواسطة Brans - Dicke . من أجل استعادة الجاذبية الموجودة في كوننا ، من الضروري "التخلص" من ستة أبعاد وتوجيه ثابت الاقتران ω إلى ما لا نهاية.
إذا سمعت مصطلح "الدمج" كما هو مطبق على نظرية الأوتار ، فهي مجرد كلمة تعني أنه يجب علينا حل هذه الألغاز. حتى الآن ، اقترح العديد من الأشخاص حلاً كاملاً ومقنعًا مناسبًا للضغط. لكن السؤال عن كيفية الحصول على جاذبية أينشتاين وأبعاد 3 + 1 من نظرية 10 أبعاد لا يزال مفتوحًا.
 إسقاط ثنائي الأبعاد لمشعب Calabi-Yau ، إحدى الطرق الشائعة لضغط القياسات الإضافية غير الضرورية لنظرية الأوتار
إسقاط ثنائي الأبعاد لمشعب Calabi-Yau ، إحدى الطرق الشائعة لضغط القياسات الإضافية غير الضرورية لنظرية الأوتارتقدم نظرية الأوتار مسارًا إلى الجاذبية الكمومية التي يمكن مقارنتها ببعض البدائل. إذا توصلنا إلى استنتاجات معقولة حول كيفية عمل الرياضيات ، فيمكننا الحصول عليها من كل من النسبية العامة والنموذج القياسي. اليوم ، هذه هي الفكرة الوحيدة التي تعطينا ذلك - لذلك يتم متابعتها بشدة. لا يهم ما إذا كنت تدافع عن نجاح نظرية الأوتار أو الفشل ، أو كيف تشعر حيال عدم وجود تنبؤات يمكن التحقق منها ، فهي بلا شك واحدة من أكثر مجالات البحث نشاطًا في الفيزياء النظرية. في الواقع ، تبرز نظرية الأوتار باعتبارها الفكرة الرائدة بين أحلام الفيزيائيين في النظرية النهائية.