"لكننا نصنع الصواريخ!"

في مقال سابق ، تحققت مما إذا كان من الممكن ضبط وحدة تحكم غامضة تلقائيًا باستخدام "الطرق القياسية" للتحسين. اتضح أنه ممكن ونتائج الضبط التلقائي مرضية للغاية. على الأقل للصاروخ الذي تم استخدام نموذجه.

بالنسبة لكائنات التحكم غير الثابتة حيث تختلف معلمات الكائن عبر نطاقات واسعة ، فقد لا توفر وحدة التحكم الغامضة جودة تحكم كافية في جميع نطاقات التشغيل. في هذه الحالة ، من الضروري استخدام وحدة تحكم غامضة مع "توليف متعدد القنوات".

دعونا نتحقق مما إذا كان من الممكن تكوين مثل هذا المنظم باستخدام طرق التحسين القياسية.
ضع في اعتبارك توليف وحدة تحكم غامضة مع ضبط متعدد القنوات لتثبيت صاروخ باليستي في زاوية الملعب. كما هو مطلوب في التعليقات ، سيكون الصاروخ FAU-2. نستخدم مثالاً من نفس الكتاب بقلم ف. جوستيف. "منظمات غامضة في أنظمة التحكم الآلي."

جميع المصطلحات المستخدمة في هذا النص مأخوذة من هذا الكتاب وقد لا تتوافق مع المصطلحات الصارمة لنظرية التحكم الآلي.

بيان المشكلة

إن الصاروخ الباليستي الذي يستخدم عددًا كبيرًا من أنظمة التحكم المحلية هو عنصر تحكم غير ثابت إلى حد كبير. تختلف وظائف النقل ، التي تصف الصاروخ كجسم تحكم ، عن وظائف النقل للطائرات المجنحة من حيث أنها تحتوي على روابط غير مستقرة ، وبالتالي فإن حركة صاروخ غير منضبط على مسار مبرمج سيكون غير مستقر.

أدناه نعتبر نظام تثبيت صاروخ باليستي في زاوية الملعب (قناة الحركة الطولية). يتكون النظام من العناصر الضرورية وظيفيا التالية:
عنصر مقارنة (جيروسكوب مجاني مع مستشعر قياس الجهد يتميز بمعاملات Kp) ؛
مضخم الطاقة كو ، ومعدات التوجيه الهيدروليكية.

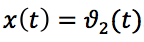
أخذ زاوية الملعب أثناء تنسيق خروج الصاروخ ، لتنسيق الإدخال - زاوية التوجيه نحدد دالة التحويل بالصيغة التالية:


(يتم تضمين ترس التوجيه والصاروخ التماثلي في عنصر التحكم) ستكون معلمات وظيفة النقل متعددة الحدود تعتمد على الوقت. رياضيا ، يمكن تحديدها بواسطة كثيرات الحدود:











تفترض المهمة أن وقت بدء الرحلة هو 6 ثوانٍ. يتم قبول قيم كثيرات الحدود بنوبة 6 ثوان.
يتم وصف النموذج الرياضي للارتباط التذبذب غير الثابت بالمعادلة التفاضلية:



يتم وصف النموذج الرياضي لارتباط التأثير غير المستقر بالمعادلة التفاضلية:



خطأ عدم التطابق عند إدخال وحدة التحكم الغامضة هو الفرق بين المجموعة وزاوية الملعب المطلوبة.

يظهر الرسم التخطيطي للنموذج في الشكل 1. من أجل فهم مبدأ تكوين النموذج ، تشير خطوط الاتصال إلى المتغيرات X1 و X ومشتقاتها ( X1 '' و X1 '' و X ' ) وفقًا لمعادلات الروابط. يشير المستطيل الأخضر إلى جزء من دائرة النموذج المطابق للرابط المتذبذب ، والجزء الأصفر هو رابط التأثير.

يتم تعيين المعلمات a (t) و b (t) و c (t) و r (t) في شكل عوامل تضخيم في كتل من نوع "مكبر للصوت". معلمة يتم تعيين في كسب ارتباط التكامل.


الشكل 1. الشكل التخطيطي للنموذج.

مسار البرنامج ، مع إعطاء زاوية الملعب u (t) = 1 + 0.5sin (πt / 30).
يتم عرض الرسوم البيانية للتغيرات في معلمات الصواريخ خلال الرحلة في الشكل 2.
تؤخذ قيمة t = 6 كبداية الرحلة ؛ في دالة كثير الحدود ، يتم استخدام القيمة (time + 6) لحساب المعلمات ، حيث يكون الوقت هو وقت المحاكاة الحالي.


الشكل 2. الرسوم البيانية للتغيرات في معلمات الصواريخ.

تحكم المنطق الضبابي

كوحدة تحكم قائمة على منطق ضبابي ، نستخدم وحدة التحكم الموضحة في الشكل 3. يتم تطبيق عدم تطابق بين زاوية الملعب المحددة وزاوية درجة الصاروخ الحقيقية على الإدخال.

يوفر تأخير الكتلة لكل خطوة تكمية تقديرًا تقديريًا لتحويل إشارة مستمرة إلى إشارة منفصلة بخطوة أخذ عينات تبلغ 0.01 ثانية.

باستخدام تأخيرين إضافيين ، يتم حساب الانحرافين الأول والثاني عن طريق طرق الاختلاف في خطوة التقسيم.

تحسب الوحدات التدريجية قيم شروط الانحراف ومعدل التغيير والتسارع. (للمزيد عن هذا راجع النص السابق ). عند الخروج من كل كتلة من المراحل ، نحصل على متجه المصطلحات للمتغيرات اللغوية. (انظر الجدول 1)

المتغير اللغوي	الشروط
انحراف	المزيد نورم أقل
معدل التغيير	ينمو لا يتغير يسقط
تغيير أسرع	يتزايد ثابت ينقص

تقوم كتل demultiplexer بتحليل المتجهات إلى مصطلحات منفصلة ، والتي يتم إرسالها إلى كتل المعالجة المنطقية وفقًا لقواعد الاستدلال الغامض.
نتيجة الاستدلال الغامض لها ثلاثة متغيرات لغوية: "اختزال" ، "لا تتغير" ، "زيادة". قواعد الاستدلال التالية مكتوبة على شكل رسم بياني.

• إذا زاد معدل النمو والنمو => النقصان .
• إذا كانت القاعدة ، ولا تتغير وهي ثابتة => فنحن لا نتغير .
• إذا كان أقل وسقوط وزاد معدل الانخفاض => زيادة .

الشكل 3. مخطط منظم على أساس منطق غامض.

في إزالة التحلل ، يتم استخدام الدوال المثلثة ذات القاعدة المشتركة كدالة عضوية (انظر الشكل 4)

الشكل 4 الشكل 4. وظائف مراحل الثلاثي مع قاعدة مشتركة.

من المفترض أن الدالات متماثلة فيما يتعلق ب 0 ، في هذه الحالة ، لوصف ثلاث وظائف مثلثة ، قيمة واحدة كحد أقصى كافية. بالنسبة لتلك الموضحة في الشكل ، الحد الأقصى = 30.

يتم استخدام نفس وظائف العضوية للإخراج.

للحصول على تعريف كامل للمنظم ، من الضروري تعيين القيم القصوى لكتل ​​تغير الطور:

- deltaMax - أقصى انحراف ؛
- divMax - أقصى مشتق للانحراف ؛
- div2Max - المشتق الثاني الأقصى للانحراف ؛
- uMax - إجراء التحكم الأقصى.

تحسين كامل للعملية

يتم اتخاذ إجراء التحكم الأقصى يساوي uMax - 70.
وبالتالي ، يبقى لنا اختيار 3 معلمات لوظيفة تبديل الطور.
في هذه المشكلة ، يتم تغذية عدم التطابق بخطوة في لحظة الصفر من وقت النموذج ، u (t) = 1 + 0.5.sin (πt / 30).

المسار المبرمج ، زاوية الملعب المعطاة u (t) = 1 + 0.5sin (πt / 30) ، يسبب تأثيرًا تدريجيًا في الثانية الأولى من عملية الانتقال ، كما اتضح أثناء التجارب مع المهمة السابقة ، يمكن ضبط وحدات التحكم على عملية تحكم سلسة ، مع إجراء تدريجي ، لا توفر الجودة المطلوبة لعملية الانتقال.

لذلك ، للتحسين ، نشكل 3 معايير:

1. الوقت العابر - يجب أن نصل إلى مسار برنامج معين بأسرع وقت ممكن.
2. الانحراف المعياري.
3. عدد عمليات التحويل - في التجارب على المهمة السابقة ، حصلنا على الخيار عندما كانت هناك تذبذبات عالية التردد لإجراء التحكم عند الإخراج في نظام التحكم.

يظهر المخطط العام لكتلة التحسين في الشكل 5.

الشكل 5 الشكل 5. مخطط كتلة التحسين.

معلمات إدخال كتلة التحسين:

- الانحراف عن زاوية الميل المحددة.
- الأثر التنظيمي.

لحساب الوقت العابر ، يتم استخدام المفتاح الذي يتم تطبيق وقت النموذج الحالي فيه على أحد المدخلات. بعد الفاصل ، هناك تأخير لفترة التكمية ، يتم إرسال القيمة من التأخير إلى الإدخال الثاني.

كمفتاح ، يتم استخدام وحدة الانحراف. إذا كانت وحدة الانحراف أكبر من قيمة التحويل المحددة (0.02) ، فسيتم إخراج الوقت الحالي عند الكتلة ؛ إذا كانت الوحدة أقل من القيمة المحددة ، فإن الوقت المخزن عندما كان الانحراف أكبر ينتقل إلى الإخراج. إذا تجاوز الانحراف الحد مرة أخرى ، نحصل على الوقت مرة أخرى. وبالتالي ، عند المخرج لدينا دائمًا آخر مرة تجاوز فيها الانحراف القيمة المحددة.
كوحدة التبديل ، يتم تغيير علامة إجراء التحكم من + إلى -. لحساب عدد المحولات ، نستخدم كتلة "الدافع على طول المقدمة" ، والتي عندما يتم تغيير المدخلات من 0 إلى 1 ، تعطي نبضة المدة في خطوة التكامل ، يتم حساب النبضات من قبل المكمل. عند الخروج من الكتلة - عدد المفاتيح.

- تختار كتلة التحسين قيم المعلمات التي يتعين تحسينها بطريقة تقلل من جميع المعلمات الثلاث:
- deltaMax - أقصى انحراف ؛
- divMax - أقصى مشتق للانحراف ؛
- div2Max - المشتق الثاني الأقصى للانحراف.

والنتيجة هي تحسين عملية الانتقال الكاملة.

بعد أن بدأنا عملية التحسين ، حصلنا على المعلمات المثلى التالية لوحدة التحكم الغامضة:

- deltaMax = 0.185– أقصى انحراف ؛
- divMax = 0.278 - أقصى مشتق للانحراف ؛
- div2Max = 1.291 - أقصى مشتق ثان للانحراف.

تظهر نتائج العملية المثلى في الشكل 6.

الشكل 6 أ. عملية الانتقال.

الشكل 6 ب. خيارات التحكم.

يمكن ملاحظة أن التحسين ، بشكل عام ، كان ناجحًا ، ولكن الانحرافات عن زاوية الملعب موجودة تقريبًا طوال العملية. يوضح الرسم البياني للانحراف الموسع أن الانحرافات بعد التحسين وإكمال عملية الانتقال تقع في نطاق 0.015 - 0.02. (انظر الشكل 7)

الرقم 7 الشكل. الانحراف في عملية التحكم.

التحسين عن طريق أقسام الرحلة.

دعونا نحاول تحسين العملية من خلال تحديد معلمات وحدة التحكم الغامضة لأقسام مختلفة من رحلة الصواريخ.

القسم الأول هو الوقت من البداية للخروج على مسار معين. استنادًا إلى الرسم البياني للانحراف ، تنتهي عملية الانتقال المرتبطة بالتأثير التدريجي الأولي في مكان ما في 20 ثانية. (انظر الشكل 7). في هذا القسم ، يحدث تحسين الوقت لعملية الانتقال.

اضبط وقت انتهاء الحساب على 20 ثانية. وسنقوم بإجراء التحسين ، وإزالة الانحراف المعياري من المعايير. سنقوم بالتحسين بحلول وقت عملية الانتقال وعدد التبديل. يظهر مخطط كتلة التحسين في الشكل 8.


الشكل 8. مخطط التحسين في المرحلة الأولى من الرحلة.

أنتج التحسين التلقائي للمرحلة الأولى من الرحلة حتى 20 ثانية المعلمات التالية للتنظيم الغامض:

- deltaMax = 0.056– أقصى انحراف ؛
- divMax = 0.0968 - أقصى مشتق للانحراف ؛
- div2Max = 0.987 - المشتق الثاني الأقصى للانحراف.

يظهر الشكل 9 عملية الانتقال بعد التحسين.

ويظهر الشكل 10 انحرافات على نطاق أكبر.

الشكل 9 أ. عملية الانتقال.

الشكل 9 ب. خيارات التحكم.

الشكل 10. انحراف أكبر في المحطة الأولى من الرحلة.

تظهر الرسوم البيانية أن التجاوز قد انخفض وأن الانحراف بعد نهاية العملية الانتقالية أصبح أقل من 0.005.

للتحسين في قسم الطيران التالي ، سنقوم بالمحاكاة مع الحالة المحفوظة التي تم الحصول عليها في القسم الأول.

تتم المحاكاة من 20 إلى 40 ثانية من رحلة الصواريخ البالستية ، يحدث التحسين طوال العملية.

نظرًا لأننا أكملنا عملية الانتقال في بداية القسم الثاني ، فإننا نقوم بالتحسين فقط من خلال الانحراف وعدد المفاتيح. يظهر مخطط كتلة التحسين في الشكل 11.


الشكل 11. مخطط التحسين لقسم الرحلة الثانية.

أنتج التحسين التلقائي للمرحلة الثانية من الرحلة من 20 إلى 40 ثانية المعلمات التالية للتنظيم الغامض:

- deltaMax = 0.056– أقصى انحراف ؛
- divMax = 0.0974 - أقصى مشتق للانحراف ؛
- div2Max = 0.980 - المشتق الثاني الأقصى للانحراف.

مع المعلمات المعطاة ، ينحرف انحراف زاوية الملعب عن معين خلال المقطع الزمني الكامل للرحلة. ولكن إذا استخدمنا المعلمات التي تم الحصول عليها عن طريق التحسين في الجزء الثاني من الرحلة للتحكم حتى 66 ثانية ، فيمكن ملاحظة أن الدقة تبدأ في الانخفاض ويبدأ الانحراف في الزيادة بعد 40 ثانية (انظر الشكل 12).


الشكل 12. عملية التحكم في الصواريخ البالستية مع إعدادات الأمثل ل 20-40 رحلة ثانية.

كرر تحسين المحطة الثالثة من الرحلة. احفظ النتائج لمدة 40 ثانية.

نستخدمها للبدء والتحسين في قسم من 40 إلى 66 ثانية.

أنتج التحسين التلقائي لقسم الرحلة الأخيرة من 40 إلى 66 ثانية المعلمات التالية للتنظيم المشوش:

- deltaMax = 0.0146– أقصى انحراف ؛
- divMax = 0.0157– أقصى مشتق للانحراف ؛
- div2Max = 0.555 - المشتق الثاني الأقصى للانحراف.

يظهر الرسم البياني لعملية التحكم في القسم الأخير من رحلة الصواريخ الباليستية بعد التحسين في الشكل 13.

الشكل 13. عملية السيطرة على الصواريخ البالستية في المحطة الأخيرة من الرحلة.

يوضح الشكل 13 أنه مع الإعدادات الجديدة ، لا يزيد الانحراف في الفاصل الزمني لرحلة الطيران من 40-66 ثانية ، على عكس الإعدادات المحسنة لقطاع الطيران الثاني (انظر الشكل 12).

وبالتالي ، حصلنا على إعدادات وحدة التحكم المشوشة لثلاثة أقسام من الرحلة. لنقم بإنشاء مفتاح تبديل يعمل على تبديل إعدادات وحدة التحكم أثناء الرحلة. يتم عرض دائرة تبديل الوضع في الشكل 14.


الرقم 14 الشكل. وضع التبديل من وحدة تحكم الصواريخ الباليستية غامض.

ستحدث أوضاع التبديل في الوقت المناسب ، في الجزء العلوي تقارن دائرة منطقية بسيطة بين وقت النموذج الحالي ونقاط التبديل. ونتيجة لذلك ، يتم تشكيل ناقل تحكم من ثلاث قيم في معدد الإرسال. في هذا المتجه ، تكون القيمة 1 في موضع الفاصل الزمني الحالي.

يتم تجميع معلمات وحدة التحكم المشوشة المحسوبة سابقًا بواسطة طرق التحسين في ناقلات ذات ثلاث قيم.

بمساعدة كتلة أخذ العينات المكونة من ثلاث قيم ، يتم اختيار واحدة تتوافق مع 1 في ناقل التحكم ، وبالتالي ، عندما يتغير الوقت ، تتغير المعلمات المنقولة إلى وحدة التحكم الغامضة وفقًا لقسم الطيران الحالي.

للتوضيح ، يتم عرض القيم المرسلة عبر خط الاتصال في الرسم التخطيطي. هذا الرقم يتوافق مع القسم الأخير من رحلة صاروخ باليستي. الوقت أكثر من 40 ثانية. متجه التحكم (0،0،1) في وحدة التحكم هو المعلمة الأخيرة من المجموعة.

يتم عرض نتيجة المحاكاة للتحكم في زاوية ميل الصاروخ مع تبديل معلمات المنظم في الشكل 15.

الشكل 15 أ. عملية الانتقال.

الشكل 15 ب. خيارات التحكم.

الاستنتاجات:
يمكن تكوين وحدة تحكم تعتمد على المنطق الضبابي من خلال طريقة التحسين للعمل في وضع تبديل المعلمة.

انخفض الانحراف عند العمل مع المعلمات المتغيرة في المثال المحدد بمقدار 3-5 مرات مقارنة بتشغيل وحدة التحكم مع المعلمات الثابتة.

يمكن تنزيل الأرشيف بمشروعات الدراسة المستقلة هنا ...