الجوهر العام لفرز الإدراج هو كما يلي:
- يكرر العناصر الموجودة في الجزء غير المصنف من الصفيف.
- يتم إدراج كل عنصر في الجزء المصنف من المصفوفة في المكان الذي يجب أن يكون فيه.
هذا ، من حيث المبدأ ، كل ما تحتاج إلى معرفته حول الفرز حسب الإدخالات. أي أن أنواع الإدراج تقسم المصفوفة دائمًا إلى قسمين - مفروزين وغير مفروزين. يتم استرداد أي عنصر من الجزء غير المفرز. نظرًا لأنه يتم فرز الجزء الآخر من الصفيف ، يمكنك العثور بسرعة على مكانك في هذا الصفيف لهذا العنصر المستخرج. يتم إدراج العنصر عند الضرورة ، ونتيجة لذلك يزداد الجزء المصنف من الصفيف ، وينقص الجزء غير المصنف. هذا كل شيء. تعمل جميع أنواع الإدخالات وفقًا لهذا المبدأ.
أضعف نقطة في هذا النهج هو إدراج عنصر في الجزء المصنف من الصفيف. في الواقع ، الأمر ليس سهلاً وما هي الحيل التي لا يتعين عليك اتخاذها لإكمال هذه الخطوة.
فرز بسيط للإدخال

ننتقل عبر الصفيف من اليسار إلى اليمين ونعالج كل عنصر على حدة. على يسار العنصر التالي ، نزيد الجزء المصنف من الصفيف ، إلى اليمين ، مع تقدم العملية ، يتبخر الجزء غير المصنف ببطء. في الجزء المصنف من الصفيف ، يتم البحث عن نقطة الإدراج للعنصر التالي. يتم إرسال العنصر نفسه إلى المخزن المؤقت ، ونتيجة لذلك تظهر خلية فارغة في المصفوفة - وهذا يسمح لك بتغيير العناصر وتحرير نقطة الإدراج.
def insertion(data): for i in range(len(data)): j = i - 1 key = data[i] while data[j] > key and j >= 0: data[j + 1] = data[j] j -= 1 data[j + 1] = key return data
باستخدام إدخالات بسيطة كمثال ، فإن الميزة الرئيسية لمعظم (وليس كل!) الفرز حسب الإدخالات تبدو بشكل واضح ، وهي المعالجة السريعة جدًا للمصفوفات المرتبة تقريبًا:

في هذا السيناريو ، من المرجح أن يتجاوز التطبيق الأكثر بدائية لإدخالات الفرز الخوارزمية فائقة التحسين لبعض الفرز بسرعة ، بما في ذلك في المصفوفات الكبيرة.
يتم تسهيل ذلك من خلال الفكرة الرئيسية لهذه الفئة - نقل العناصر من الجزء غير المصنف من الصفيف إلى الفرز. مع قرب البيانات ذات الحجم المماثل ، عادةً ما تقع نقطة الإدراج بالقرب من حافة الجزء الذي تم فرزه ، مما يسمح لك بإدخاله مع أقل حمل.
لا يوجد شيء أفضل للتعامل مع المصفوفات المرتبة تقريبًا من فرز الإدخال. عندما تقابل معلومات في مكان ما يكون أفضل تعقيد زمني للفرز حسب الإدخالات هو
O ( n ) ، فأنت على الأرجح تشير إلى مواقف ذات صفائف مرتبة تقريبًا.
فرز حسب إدراجات البحث الثنائية البسيطة

نظرًا لأنه يتم البحث عن المكان المطلوب إدراجه في الجزء المصنف من الصفيف ، فإن فكرة استخدام البحث الثنائي توحي بنفسها. شيء آخر هو أن البحث عن موقع الإدراج ليس حاسمًا لتعقيد الوقت للخوارزمية (مصدر الطعام الرئيسي هو مرحلة إدخال العنصر في الموضع الذي تم العثور عليه نفسه) ، وبالتالي فإن هذا التحسين لا يفعل سوى القليل.
وفي حالة وجود مصفوفة تم فرزها تقريبًا ، يمكن أن يعمل البحث الثنائي بشكل أبطأ ، نظرًا لأنه يبدأ من منتصف قسم الفرز ، والذي سيكون على الأرجح بعيدًا جدًا عن نقطة الإدراج (وسيتطلب خطوات أقل لإجراء بحث عادي من موضع العنصر إلى نقطة الإدراج إذا كانت البيانات في الصفيف ككل أمر).
def insertion_binary(data): for i in range(len(data)): key = data[i] lo, hi = 0, i - 1 while lo < hi: mid = lo + (hi - lo) // 2 if key < data[mid]: hi = mid else: lo = mid + 1 for j in range(i, lo + 1, -1): data[j] = data[j - 1] data[lo] = key return data
دفاعًا عن البحث الثنائي ، ألاحظ أنه يمكنه قول الكلمة الأخيرة في فعالية الفرز الآخر عن طريق الإدخالات. بفضله ، على وجه الخصوص ، فإن الخوارزميات مثل الفرز المكتبي والفرز سوليتير تذهب إلى متوسط التعقيد الزمني
O ( n log n ) . ولكن عنهم فيما بعد.
إقران الفرز بإدراج بسيط
تعديل الإدخالات البسيطة التي تم تطويرها في المختبرات السرية التابعة لشركة Oracle Corporation. هذا الفرز هو جزء من JDK ، وهو جزء من Dual-Pivot Quicksort. يتم استخدامه لفرز المصفوفات الصغيرة (حتى 47 عنصرًا) وفرز المساحات الصغيرة من المصفوفات الكبيرة.

لا يتم إرسال عنصر واحد بل عنصرين متجاورين إلى المخزن المؤقت في وقت واحد. أولاً ، يتم إدخال العنصر الأكبر للزوج ، وبعده مباشرة ، يتم تطبيق طريقة الإدراج البسيطة على العنصر الأصغر للزوج.
ماذا يعطي؟ وفورات للتعامل مع عنصر أصغر من زوج. بالنسبة له ، يتم البحث عن نقطة الإدراج والإدراج نفسه فقط على هذا الجزء المصنف من المصفوفة ، والذي لا يتضمن المنطقة المصنفة المستخدمة لمعالجة عنصر أكبر من الزوج. يصبح هذا ممكنًا لأن العناصر الأكبر والأصغر تتم معالجتها على الفور واحدة تلو الأخرى في مرور واحد من الحلقة الخارجية.
هذا لا يؤثر على متوسط التعقيد الزمني (لا يزال يساوي
O ( n 2 )) ، ومع ذلك ، تعمل الإدخالات المقترنة بشكل أسرع قليلاً من الإدخالات المعتادة.
أنا أوضح الخوارزميات في Python ، ولكن هنا أعطي المصدر الأصلي (المعدل للقراءة) في Java:
for (int k = left; ++left <= right; k = ++left) {
فرز شل

تمتلك هذه الخوارزمية نهجًا ذكيًا للغاية في تحديد أي جزء من الصفيف يعتبر مصنفًا. في الإدخالات البسيطة ، كل شيء بسيط: من العنصر الحالي ، يتم فرز كل شيء على اليسار بالفعل ، ولا يتم فرز كل شيء على اليمين بعد. على عكس الإدخالات البسيطة ، لا يحاول فرز Shell أن يقوم فورًا بتشكيل جزء تم فرزه بدقة من المصفوفة على يسار العنصر. يقوم بإنشاء جزء تم
فرزه تقريبًا من الصفيف إلى يسار العنصر ويقوم بذلك بسرعة كافية.
يلقي فرز Shell العنصر الحالي في المخزن المؤقت ويقارنه بالجانب الأيسر من الصفيف. إذا وجد عناصر أكبر على اليسار ، فإنه يحولها إلى اليمين ، مما يفسح المجال للإدخال. ولكن في نفس الوقت ، لا يأخذ الجزء الأيسر بأكمله ، ولكن فقط مجموعة معينة من العناصر منه ، حيث يتم تباعد العناصر عن بعضها البعض بمسافة معينة. يسمح لك هذا النظام بإدراج العناصر بسرعة في مساحة المصفوفة تقريبًا حيث يجب أن تكون موجودة.
مع كل تكرار للحلقة الرئيسية ، تنخفض هذه المسافة تدريجيًا وعندما تصبح مساوية لواحد ، يتحول نوع Shell في هذه اللحظة إلى نوع كلاسيكي مع إدخالات بسيطة ، والتي تم منحها لمعالجة صفيف تم فرزه تقريبًا. يتم إدراج فرز صفيف تم فرزه تقريبًا في فرز تم تحويله بالكامل بسرعة.
def shell(data): inc = len(data) // 2 while inc: for i, el in enumerate(data): while i >= inc and data[i - inc] > el: data[i] = data[i - inc] i -= inc data[i] = el inc = 1 if inc == 2 else int(inc * 5.0 / 11) return data
يحسن ترتيب الفرز باستخدام مبدأ مشابه فرز الفقاقيع ، لذا فإن تعقيد الخوارزمية مع
O ( n 2 ) يقفز حتى
O ( n log n ) . للأسف ، لم تتمكن شل من تكرار هذا الإنجاز - أفضل تعقيد زمني يصل إلى
O ( n log 2 n ) .
تمت كتابة العديد من هابراتاتي حول فرز شل ، لذلك لن نكون مثقلين بالمعلومات وننتقل.
فرز الأشجار
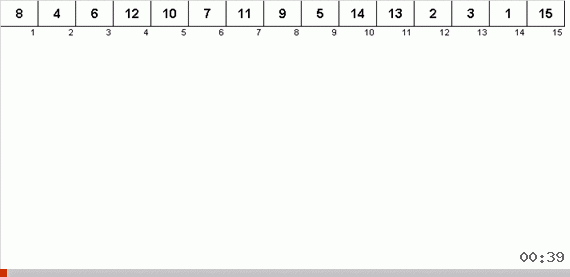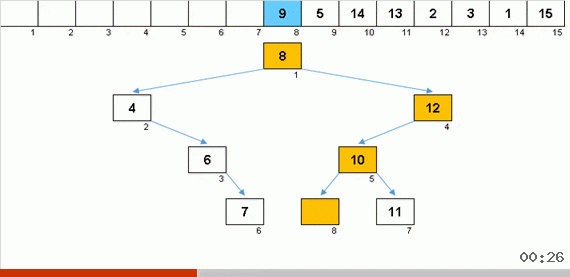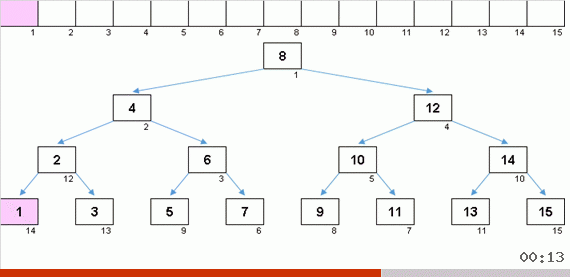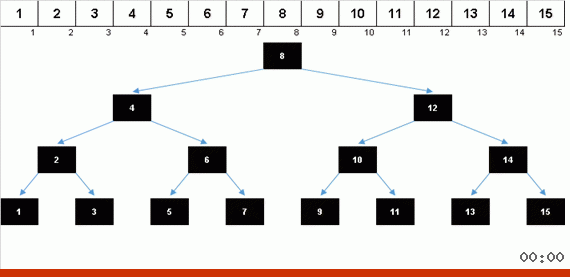
يؤدي الفرز باستخدام شجرة بسبب الذاكرة الإضافية إلى حل مشكلة إضافة عنصر آخر إلى الجزء الذي تم فرزه من المصفوفة بسرعة. علاوة على ذلك ، تعمل الشجرة الثنائية باعتبارها الجزء المصنف من الصفيف. يتم تشكيل شجرة حرفيا على الطاير عند تكرارها على العناصر.
تتم مقارنة العنصر أولاً بالجذر ، ثم بالعقد المتداخلة وفقًا للمبدأ: إذا كان العنصر أصغر من العقدة ، فإننا ننزل أسفل الفرع الأيسر ، إن لم يكن أقل ، ثم الجزء الأيمن. يمكن بعد ذلك التحايل على الشجرة التي تم إنشاؤها بواسطة هذه القاعدة بسهولة للانتقال من العقد ذات القيم الأقل إلى العقد ذات القيم الأكبر (وبالتالي الحصول على جميع العناصر بترتيب متزايد).
يتم حل المشكلة الرئيسية للفرز عن طريق إدراج (تكلفة إدراج عنصر في مكانه في الجزء المصنف من الصفيف) هنا ، يستمر البناء بسرعة كبيرة. على أي حال ، لتحرير نقطة الإدراج ، ليس من الضروري تحريك قوافل العناصر ببطء كما هو الحال في الخوارزميات السابقة. يبدو أنه هنا هو أفضل إدخالات الفرز. لكن هناك مشكلة
عندما تحصل على شجرة عيد الميلاد متناظرة جميلة (ما يسمى شجرة متوازنة تمامًا) كما هو الحال في الرسوم المتحركة ثلاث فقرات أعلاه ، يحدث الإدراج بسرعة ، لأن الشجرة في هذه الحالة لديها أدنى مستويات التعشيش الممكنة. ولكن نادرًا ما يتم الحصول على بنية متوازنة (أو على الأقل قريبة من ذلك) من صفيف عشوائي. والشجرة ، على الأرجح ، ستكون غير كاملة وغير متوازنة - مع تشوهات وأفق مملوء وعدد مفرط من المستويات.
صفيف عشوائي بقيم من 1 إلى 10. تولد العناصر في هذا الترتيب شجرة ثنائية غير متوازنة: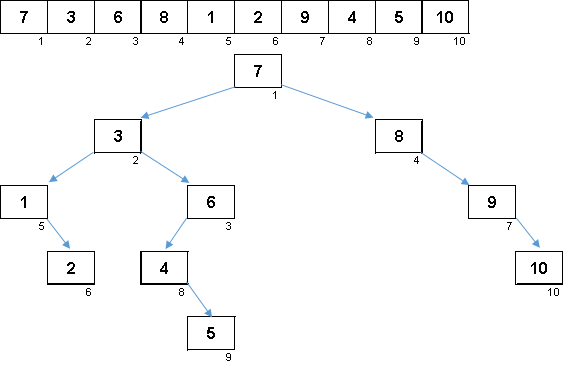
الشجرة لا تكفي للبناء ، لا تزال بحاجة إلى التحايل عليها. كلما زاد اختلال التوازن - كلما كانت خوارزمية اجتياز الشجرة أقوى. هنا ، كما تقول النجوم ، يمكن للصفيف العشوائي أن يولد عقبة قبيحة (على الأرجح) وفراكتل يشبه الشجرة.
قيم العناصر هي نفسها ، ولكن الترتيب مختلف. يتم إنشاء شجرة ثنائية متوازنة: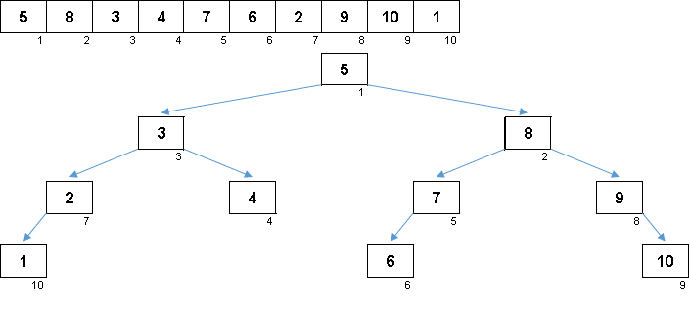
 على ساكورا الجميلة
على ساكورا الجميلة
لا يوجد بتلة كافية:
شجرة ثنائية للعشرات.يتم حل مشكلة الأشجار غير المتوازنة عن طريق الفرز العكسي ، والذي يستخدم نوعًا خاصًا من شجرة البحث الثنائية - شجرة التشتيت. هذه شجرة محولات رائعة ، يتم إعادة بنائها بعد كل عملية في حالة متوازنة. حول ذلك سيكون مقالة منفصلة. وبحلول ذلك الوقت سوف أقوم بإعداد تطبيقات Python لكل من فرز الشجرة وفرز Splay.
حسنًا ، حسنًا ، مررنا لفترة وجيزة عبر إدخالات الفرز الأكثر شيوعًا. إدخالات بسيطة وقشرة وشجرة ثنائية نعرفها جميعًا من المدرسة. الآن فكر في ممثلين آخرين لهذه الفئة ، غير معروفين على نطاق واسع.
ويكي / ويكي -
الإدراج ، شل / شل ، شجرة / شجرةمقالات سلسلة:
من يستخدم AlgoLab - أوصي بتحديث الملف. أضفت إدخالات بحث ثنائية بسيطة وإدخالات مقترنة إلى هذا التطبيق. كما أعاد كتابة التصور الكامل لـ Shell (في الإصدار السابق لم يكن هناك شيء يمكن فهمه) وأضاف تمييزًا إلى الفرع الأصلي عند إدراج عنصر في الشجرة الثنائية.