أحدثت الشبكات العصبية ثورة في مجال التعرف على الأنماط ، ولكن بسبب التفسير غير الواضح لمبدأ التشغيل ، لا يتم استخدامها في مجالات مثل الطب وتقييم المخاطر. إنه يتطلب تمثيلًا مرئيًا للشبكة ، مما يجعلها ليست صندوقًا أسودًا ، ولكن على الأقل "شفافة".
كريستوفر أولاه ، في الشبكات العصبية ، والمشعبات ، والطبولوجيا ، أظهر مبادئ تشغيل الشبكة العصبية وربطها بالنظرية الرياضية للطبولوجيا والتنوع ، والتي كانت بمثابة أساس هذه المقالة. لإثبات عمل شبكة عصبية ، يتم استخدام شبكات عصبية عميقة منخفضة الأبعاد.
بشكل عام ، ليس فهم سلوك الشبكات العصبية العميقة مهمة تافهة. من السهل استكشاف الشبكات العصبية العميقة ذات الأبعاد المنخفضة - الشبكات التي لا يوجد فيها سوى عدد قليل من الخلايا العصبية في كل طبقة. بالنسبة للشبكات منخفضة الأبعاد ، يمكنك إنشاء تصورات لفهم سلوك تلك الشبكات وتدريبها. سيوفر هذا المنظور فهمًا أعمق لسلوك الشبكات العصبية ومراقبة الاتصال الذي يجمع بين الشبكات العصبية مع مجال الرياضيات يسمى الطبولوجيا.
ويتبع ذلك عدد من الأشياء المثيرة للاهتمام ، بما في ذلك الحدود الدنيا الأساسية لتعقيد الشبكة العصبية القادرة على تصنيف مجموعات بيانات معينة.
ضع في اعتبارك مبدأ الشبكة باستخدام مثال
لنبدأ بمجموعة بيانات بسيطة - منحنيين على مستوى. ستتعلم مهمة الشبكة كيفية تصنيف النقاط التي تنتمي إلى المنحنيات.
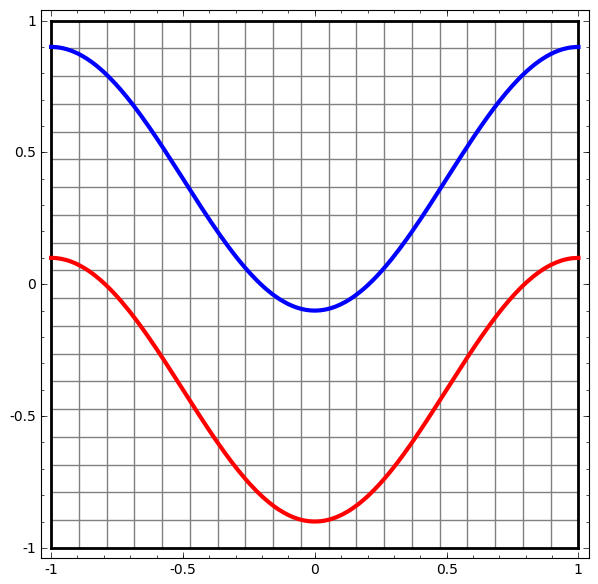
طريقة واضحة لتصور سلوك الشبكة العصبية ، لنرى كيف تصنف الخوارزمية جميع العناصر الممكنة (في مثالنا ، نقاط) من مجموعة بيانات.
لنبدأ بأبسط فئة من الشبكات العصبية ، بطبقة إدخال وإخراج واحدة. تحاول مثل هذه الشبكة فصل فئتين من البيانات بتقسيمها على خط.
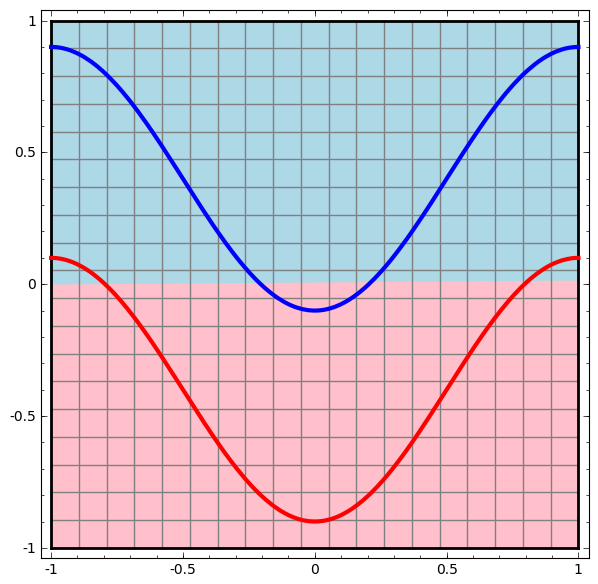
لا يتم استخدام هذه الشبكة في الممارسة. عادةً ما تحتوي الشبكات العصبية الحديثة على عدة طبقات بين مدخلاتها ومخرجاتها ، تسمى الطبقات "المخفية".
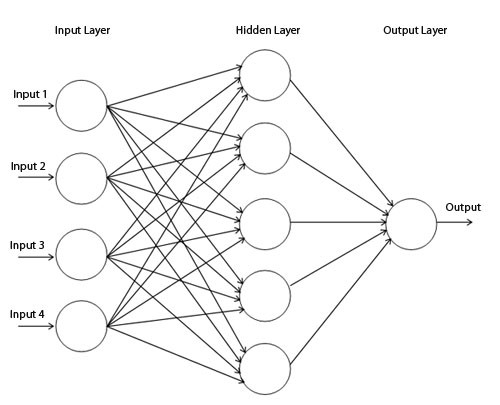
مخطط شبكة بسيط
نحن نتصور سلوك هذه الشبكة ، ونراقب ما تفعله بنقاط مختلفة في مجالها. تفصل شبكة الطبقة المخفية البيانات عن منحنى أكثر تعقيدًا من الخط.
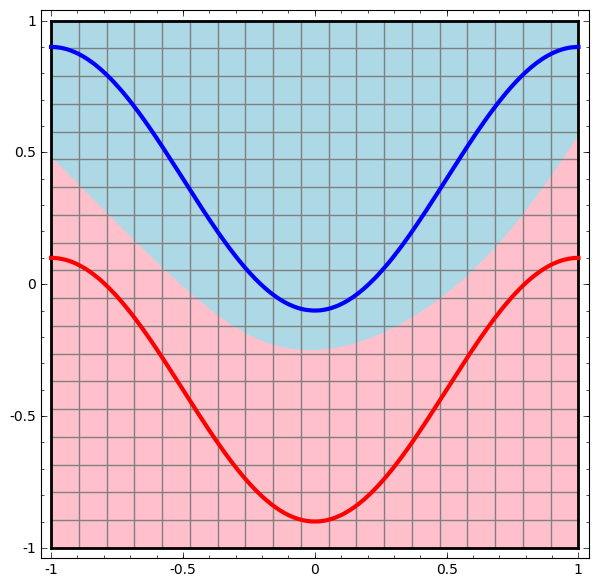
مع كل طبقة ، تقوم الشبكة بتحويل البيانات ، وإنشاء عرض جديد. يمكننا أن نرى البيانات في كل من طرق العرض هذه وكيف تصنفها الشبكة ذات الطبقة المخفية. عندما تصل الخوارزمية إلى العرض التقديمي النهائي ، ستقوم الشبكة العصبية برسم خط من خلال البيانات (أو بأبعاد أعلى - سطح مفرط).
في التصور السابق ، يتم النظر في البيانات في طريقة عرض أولية. يمكنك أن تتخيل ذلك بالنظر إلى طبقة الإدخال. الآن ، فكر في الأمر بعد تحويله إلى الطبقة الأولى. يمكنك أن تتخيل ذلك بالنظر إلى الطبقة المخفية.
يتوافق كل قياس مع تنشيط الخلايا العصبية في الطبقة.
يتم تدريب الطبقة المخفية على العرض بحيث تكون البيانات قابلة للفصل خطيًا.
تقديم الطبقة المستمرةفي النهج الموصوف في القسم السابق ، نتعلم فهم الشبكات من خلال النظر إلى العرض التقديمي المقابل لكل طبقة. هذا يعطينا قائمة منفصلة من المشاهدات.
الجزء غير التافه هو فهم كيف ننتقل من واحد إلى آخر. لحسن الحظ ، تحتوي مستويات الشبكة العصبية على خصائص تجعل ذلك ممكنًا.
هناك العديد من أنواع الطبقات المختلفة المستخدمة في الشبكات العصبية.
ضع في اعتبارك طبقة tanh لمثال محدد. تتكون طبقة Tanh-tanh (Wx + b) من:
- التحول الخطي لمصفوفة "الوزن" W
- الترجمة باستخدام المتجه ب
- تطبيق بقعة tanh.
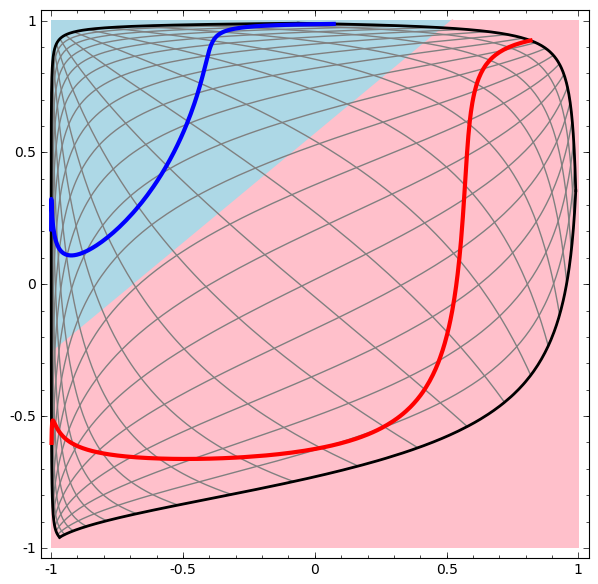
يمكننا تمثيل هذا كتحويل مستمر على النحو التالي:
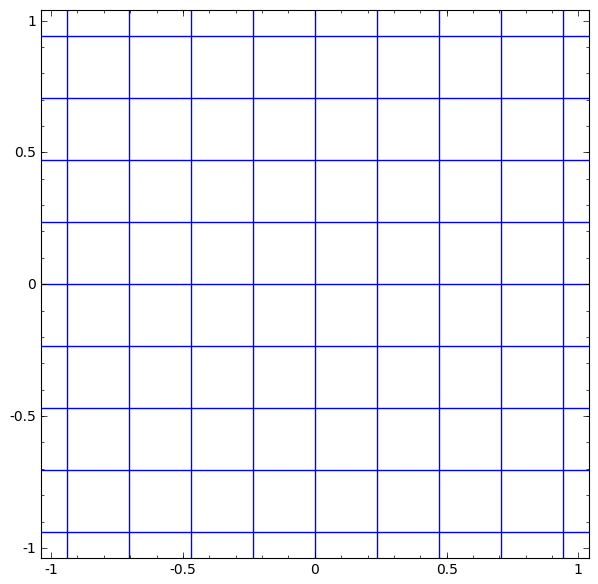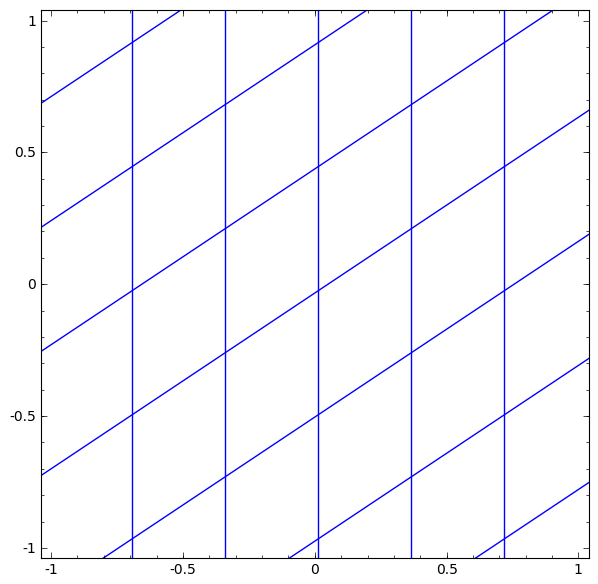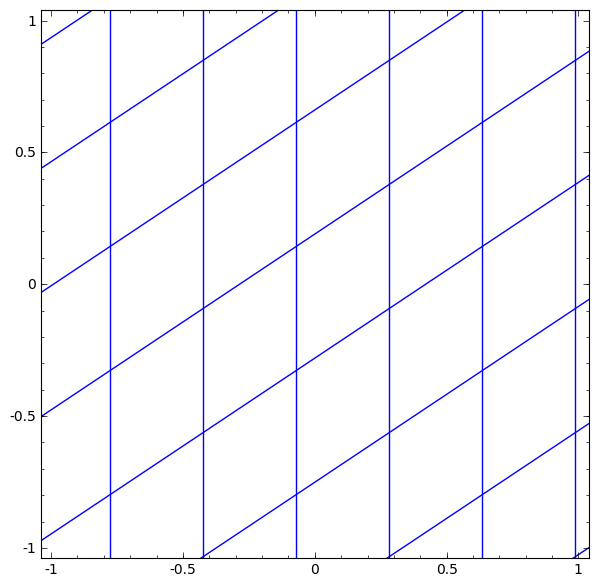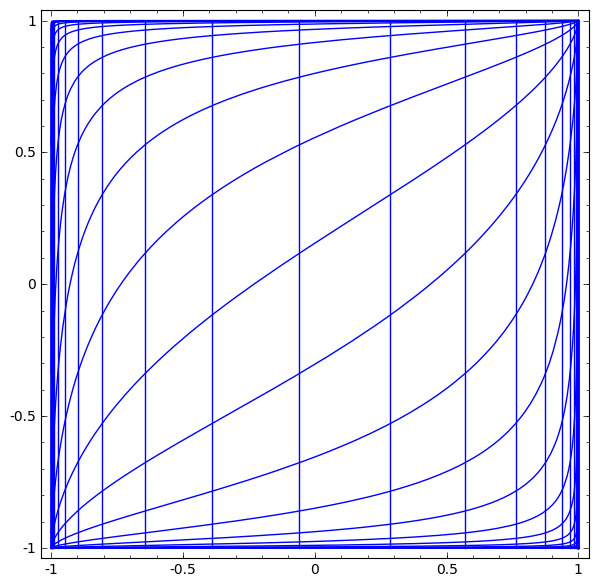
يشبه مبدأ التشغيل هذا إلى حد كبير الطبقات القياسية الأخرى التي تتكون من تحويل أفيني ، يليه التطبيق النشط لوظيفة التنشيط الرتيبة.
يمكن استخدام هذه الطريقة لفهم الشبكات الأكثر تعقيدًا. لذلك ، تصنف الشبكة التالية حلقتين متشابكتين قليلاً باستخدام أربع طبقات مخفية. بمرور الوقت ، يمكن ملاحظة أن الشبكة العصبية تنتقل من عرض خام إلى مستوى أعلى درسته الشبكة لتصنيف البيانات. في حين أن اللوالب متشابكة في البداية ، إلا أنها في النهاية قابلة للانفصال خطيًا.
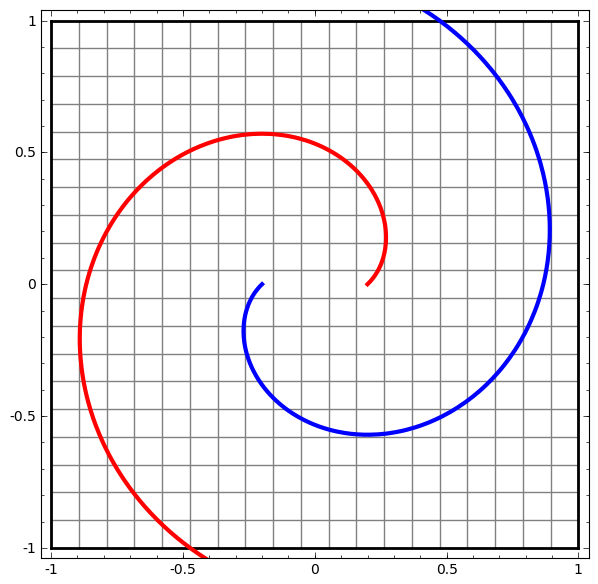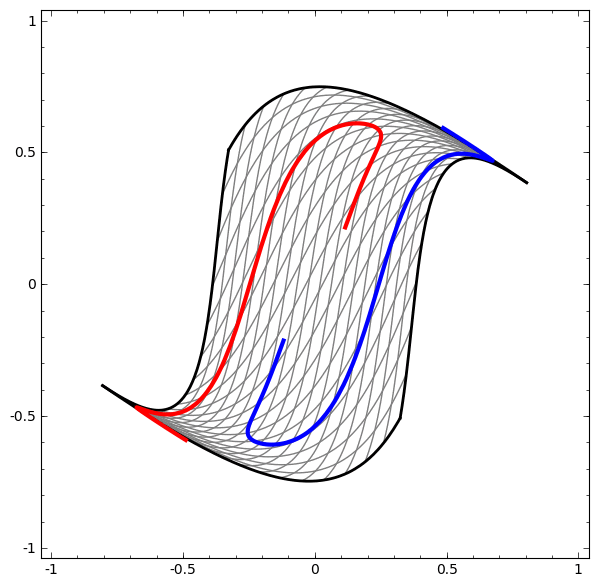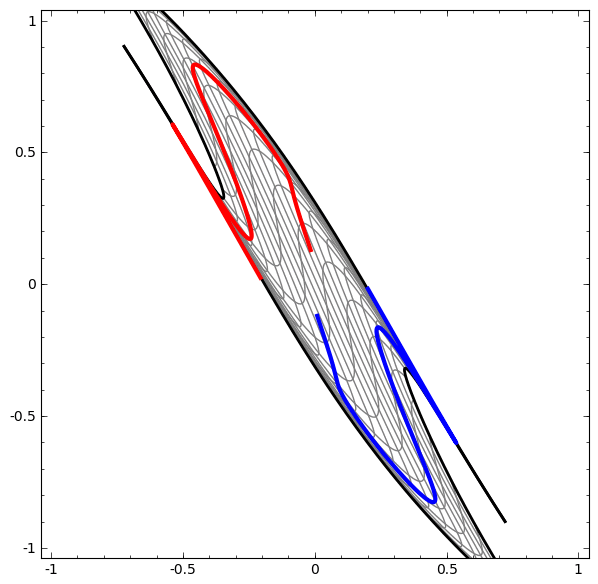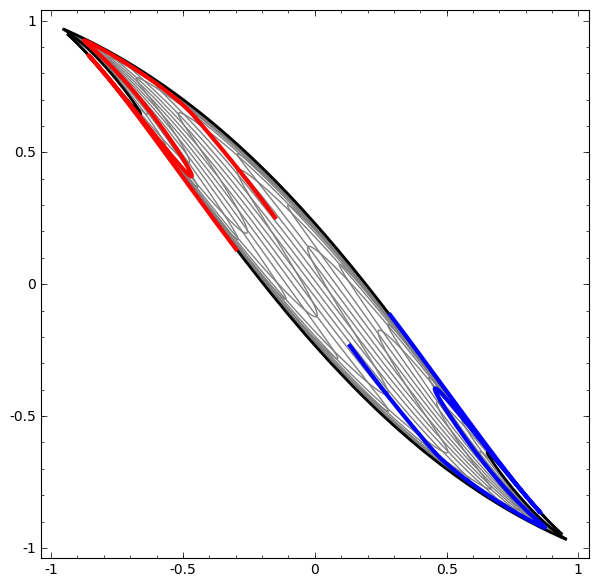
من ناحية أخرى ، الشبكة التالية ، التي تستخدم أيضًا عدة مستويات ، ولكن لا يمكنها تصنيف حلزونيين متشابكين أكثر.
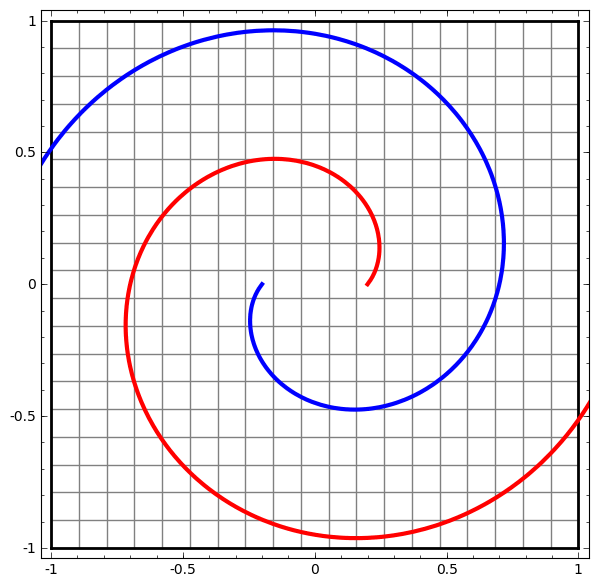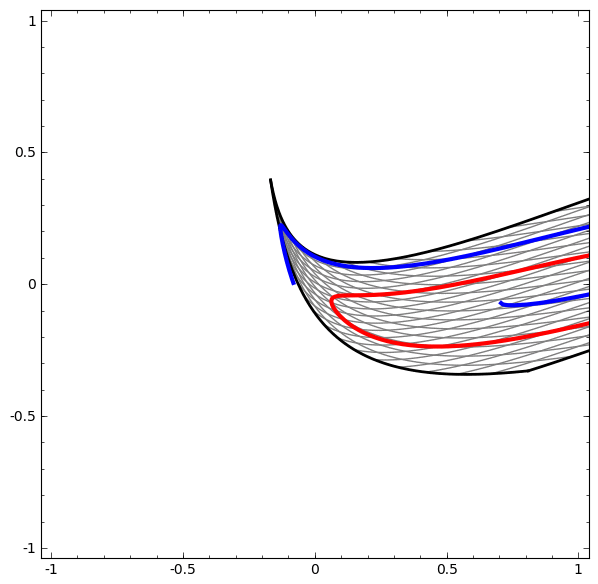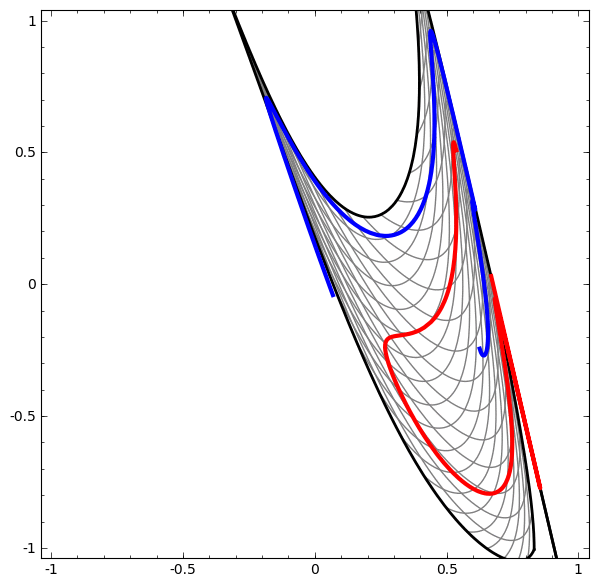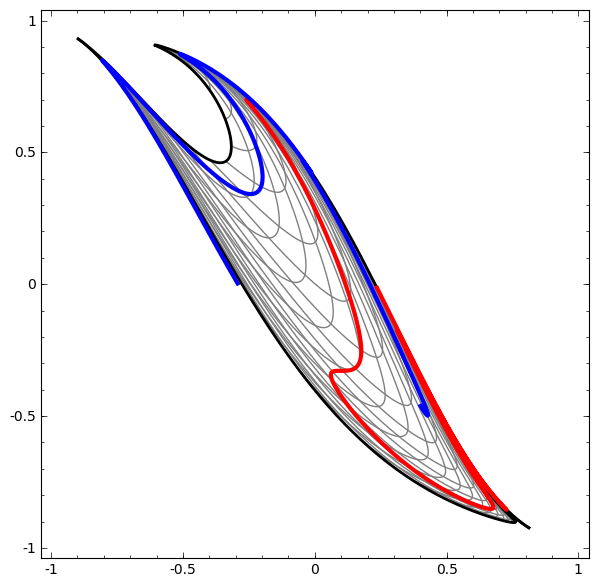
وتجدر الإشارة إلى أن هذه المهام محدودة التعقيد ، نظرًا لاستخدام الشبكات العصبية منخفضة الأبعاد. إذا تم استخدام شبكات أوسع ، فقد تم تبسيط حل المشكلات.
تانغ طبقات
كل طبقة تمدد وتضغط المساحة ، لكنها لا تقطع ، ولا تنكسر ، ولا تطويها. بشكل حدسي ، نرى أن الخصائص الطوبولوجية محفوظة في كل طبقة.
تسمى هذه التحولات التي لا تؤثر على الهيكل بالتشكيلات المتجانسة (Wiki - هذا رسم خرائط للنظام الجبري A الذي يحفظ العمليات الأساسية والعلاقات الأساسية). من الناحية الرسمية ، فإن هذه النقاط هي وظائف مستمرة في كلا الاتجاهين. في التعيين الهدف ، يتطابق كل عنصر في مجموعة واحدة مع عنصر واحد بالضبط من مجموعة أخرى ، ويتم تحديد التعيين العكسي الذي له نفس الخاصية.
النظريةالطبقات ذات المدخلات N والمخرجات N هي أشكال متجانسة إذا كانت مصفوفة الوزن W لا تتدهور. (يجب أن تكون حذرًا بشأن النطاق والنطاق.)
إثبات:1. افترض أن W له محدد غير صفري. ثم هي دالة خطية ذات اتجاه عكسي. الدوال الخطية مستمرة. لذا ، فإن الضرب في W هو تشابه.
2. الخرائط - الأشكال المتجانسة
3. tanh (كل من السيني و softplus ، ولكن ليس ReLU) هي وظائف مستمرة مع انعكاسات مستمرة. إنها مؤشرات حيوية إذا كنا حريصين على المنطقة والنطاق الذي نفكر فيه. استخدامهم نقطة هو تجانس.
وبالتالي ، إذا كان W محددًا غير صفري ، فإن الألياف متجانسة.
الطوبولوجيا والتصنيف
خذ بعين الاعتبار مجموعة بيانات ثنائية الأبعاد مع فئتين A ، B⊂R2:
أ = {س | د (س ، 0) <1/3}
B = {x | 2/3 <د (س ، 0) <1}

أحمر ، أزرق B
المتطلبات: لا يمكن للشبكة العصبية تصنيف مجموعة البيانات هذه بدون 3 طبقات مخفية أو أكثر ، بغض النظر عن العرض.
كما ذكرنا سابقًا ، فإن تصنيفًا بوظيفة سينية أو طبقة softmax يعادل محاولة العثور على طائرة مفرطة (أو خطًا في هذه الحالة) يفصل بين A و B في التمثيل النهائي. مع وجود طبقتين مخفيتين فقط ، فإن الشبكة غير قادرة طبوغرافيًا على مشاركة البيانات بهذه الطريقة ، ومحكوم عليها بالفشل في مجموعة البيانات هذه.
في التصور التالي ، نلاحظ عرضًا كامنًا أثناء تدريب الشبكة جنبًا إلى جنب مع خط التصنيف.
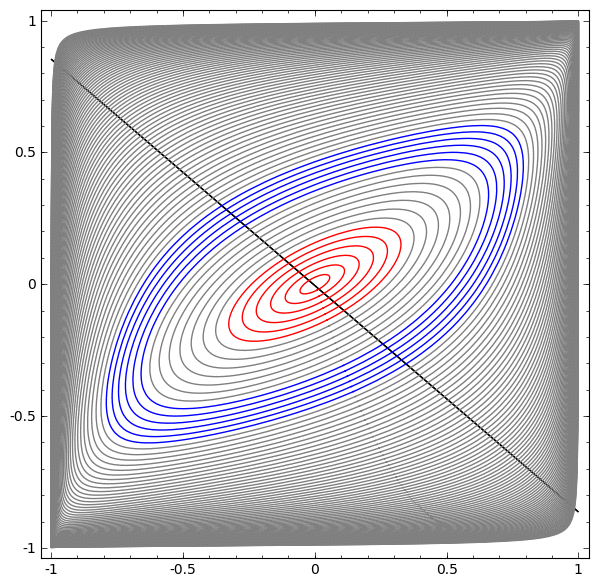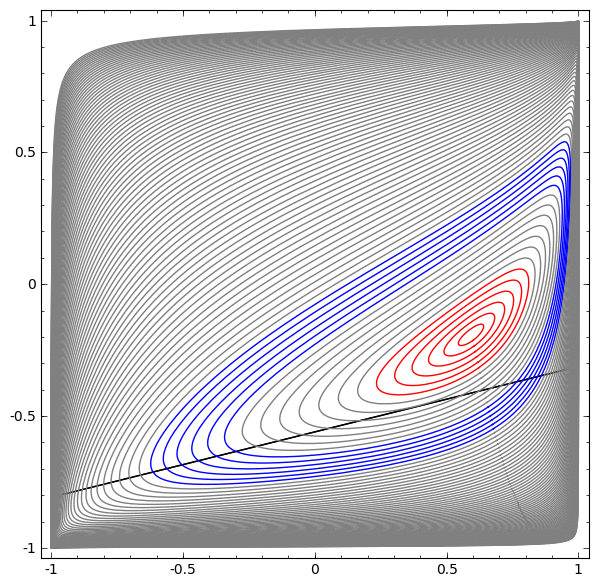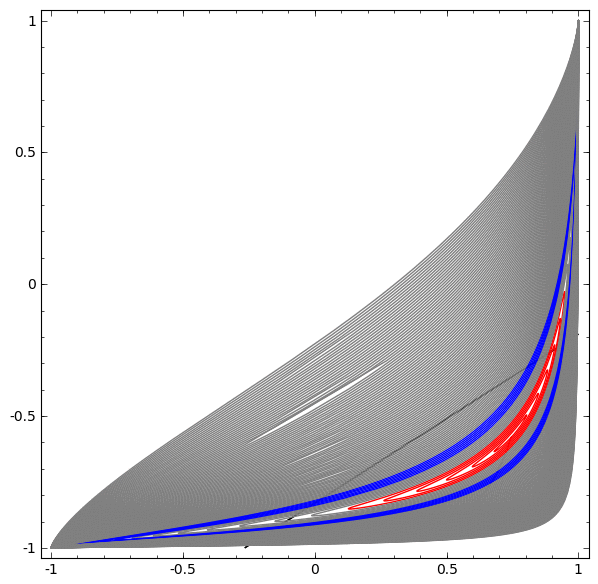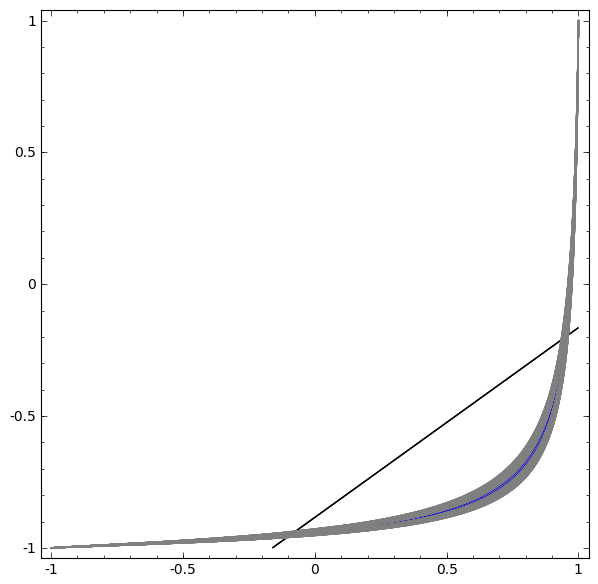
لهذه الشبكة من التدريب ليست كافية لتحقيق نتيجة مئة في المئة.
تقع الخوارزمية في الحد الأدنى المحلي غير المنتج ، ولكنها قادرة على تحقيق دقة تصنيف 80 ٪ تقريبًا.
في هذا المثال ، كانت هناك طبقة مخفية واحدة فقط ، لكنها لم تنجح.
بيان. إما أن تكون كل طبقة متجانسة ، أو أن مصفوفة الوزن للطبقة لها محدد 0.
إثبات:إذا كان هذا عبارة عن تجانس ، فإن A لا يزال محاطًا بـ B ، ولا يمكن للخط أن يفصل بينهما. ولكن لنفترض أنه يحتوي على محدد 0: ثم تنهار مجموعة البيانات على بعض المحاور. نظرًا لأننا نتعامل مع شيء متماثل في مجموعة البيانات الأصلية ، فإن A محاط بـ B ، والانهيار على أي محور يعني أنه سيكون لدينا بعض النقاط من A و B مختلطة ، وهذا يجعل من المستحيل التمييز.
إذا أضفنا عنصرًا مخفيًا ثالثًا ، فستصبح المشكلة تافهة. تعترف الشبكة العصبية بالتمثيل التالي:
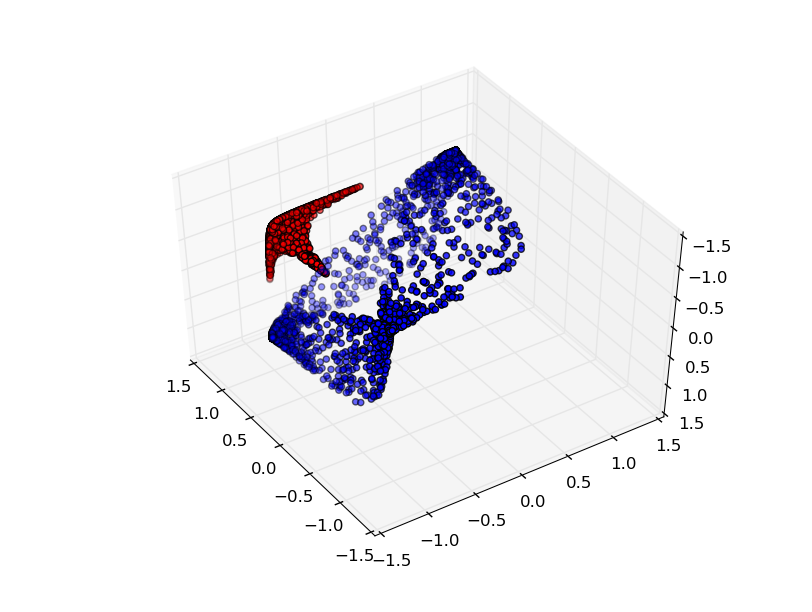
يجعل العرض من الممكن فصل مجموعات البيانات باستخدام طائرة مفرطة.
لفهم ما يجري بشكل أفضل ، دعنا نلقي نظرة على مجموعة بيانات أبسط ، وهي أحادية البعد:

أ = [- 1 / 3،1 / 3]
B = [- 1، −2 / 3] ∪ [2 / 3،1]
بدون استخدام طبقة مكونة من عنصرين مخفيين أو أكثر ، لا يمكننا تصنيف مجموعة البيانات هذه. ولكن ، إذا استخدمنا شبكة ذات عنصرين ، فسوف نتعلم كيفية تمثيل البيانات كمنحنى جيد يسمح لنا بفصل الفئات باستخدام خط:
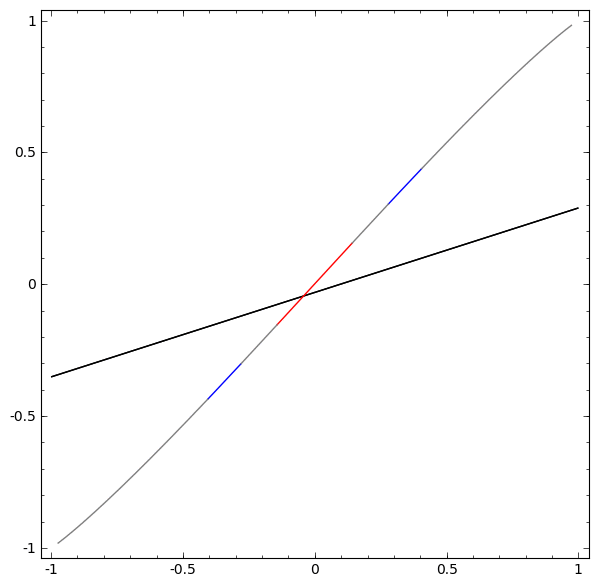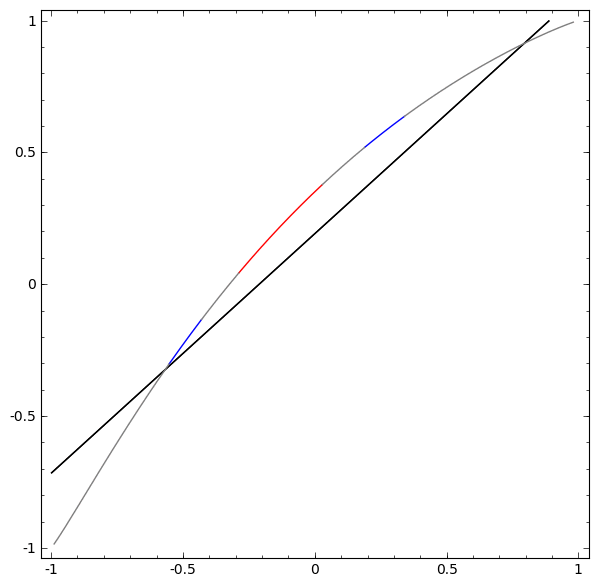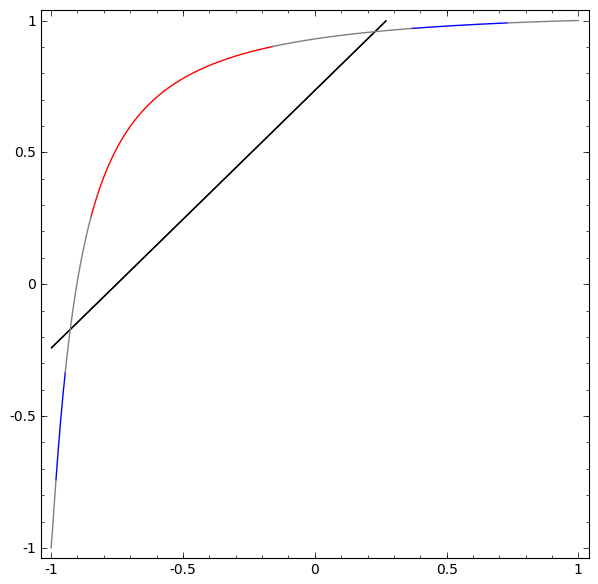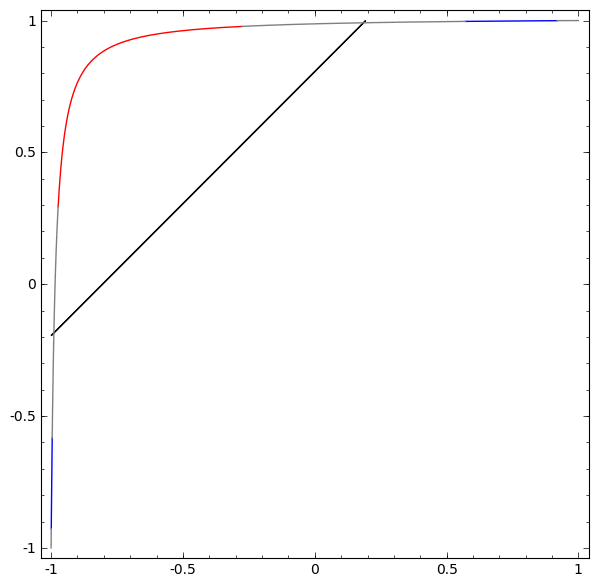
ما الذي يجري؟ يتعلم عنصر واحد مخفي إطلاق النار عند x> -1/2 ، ويتعلم أحدهم إطلاق النار عند x> 1/2. عندما يتم تشغيل الأول ، ولكن ليس الثاني ، نعلم أننا في A.
تخمين متنوعة
هل ينطبق هذا على مجموعات البيانات من العالم الحقيقي ، مثل مجموعات الصور؟ إذا كنت جادًا بشأن فرضية التنوع ، أعتقد أنها مهمة.
الفرضية المتعددة الأبعاد هي أن البيانات الطبيعية تشكل مشعبات منخفضة الأبعاد في مساحة الزرع. هناك أسباب نظرية (1) وتجريبية [2] للاعتقاد بأن هذا صحيح. إذا كان الأمر كذلك ، فإن مهمة خوارزمية التصنيف هي فصل حزمة المشعبات المتشابكة.
في الأمثلة السابقة ، أحاط أحد الصفوف الآخر تمامًا. ومع ذلك ، من غير المحتمل أن تكون مجموعة متنوعة من صور الكلاب محاطة تمامًا بمجموعة من صور القطط. ولكن هناك حالات طوبوغرافية أخرى أكثر معقولية قد لا تزال تنشأ ، كما سنرى في القسم التالي.
اتصالات وهوموتوبيز
هناك مجموعة بيانات أخرى مثيرة للاهتمام ، وهما الاتصالان المترابطان A و B.

مثل مجموعات البيانات السابقة التي فحصناها ، لا يمكن تقسيم مجموعة البيانات هذه بدون استخدام أبعاد n + 1 ، وهي البعد الرابع.
تمت دراسة الروابط في نظرية العقد ، في مجال الطوبولوجيا. في بعض الأحيان ، عندما نرى اتصالًا ، لا يتضح على الفور ما إذا كان عدم الاتساق (الكثير من الأشياء التي تتشابك معًا ولكن يمكن فصلها بالتشوه المستمر) أم لا.
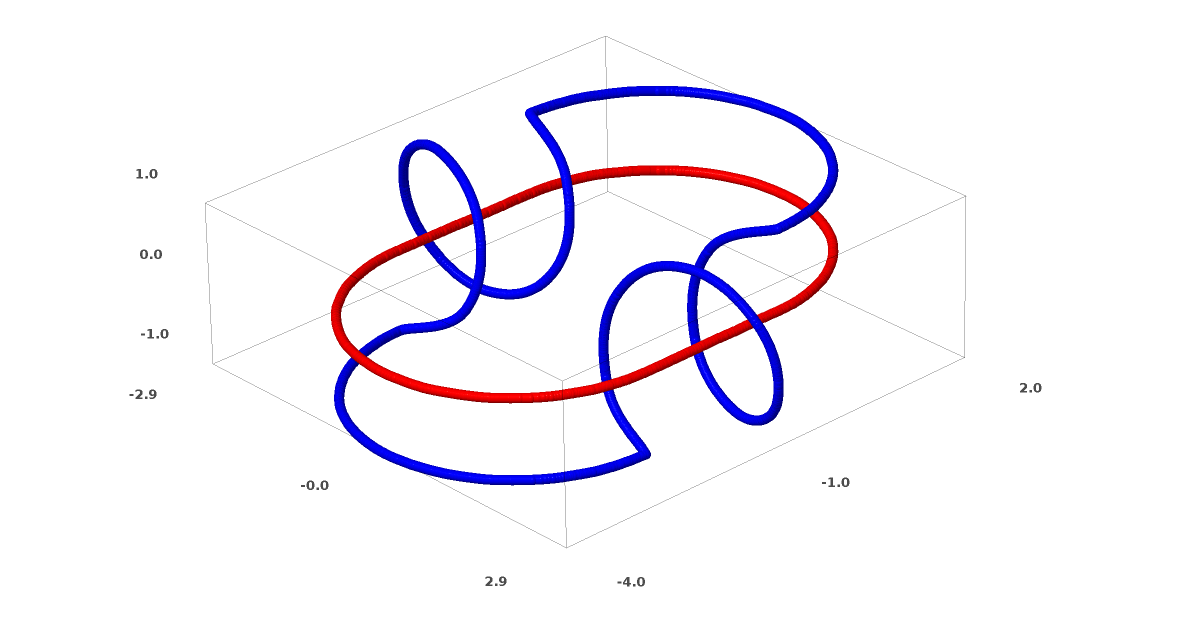
تنافر بسيط نسبيا.
إذا كانت الشبكة العصبية التي تستخدم طبقات بثلاث وحدات فقط يمكن تصنيفها ، فهي غير مترابطة. (سؤال: هل يمكن تصنيف جميع أوجه عدم الاتساق عبر الشبكة بثلاثة أوجه عدم تناسق نظريًا؟)
من وجهة نظر هذه العقدة ، فإن التصور المستمر للتمثيلات التي تم إنشاؤها بواسطة شبكة عصبية هو إجراء لفك الارتباطات. في الطبولوجيا ، سنطلق على هذا النظير المحيط بين الرابط الأصلي والرابط المنفصل.
من الناحية الشكلية ، فإن نظائر الفضاء المحيط بين الأصناف A و B هي وظيفة مستمرة F: [0،1] × X → Y بحيث أن كل قدم هو تشابه من X إلى نطاقه ، و F0 هي دالة هوية ، وخرائط F1 من A إلى B. T .ه. ينتقل Ft باستمرار من الخريطة A إلى نفسها ، إلى الخريطة A إلى B.
النظرية: هناك نظائر في المساحة المحيطة بين المدخل وتمثيل مستوى الشبكة إذا: أ) لم تتحلل ، ب) نحن مستعدون لنقل الخلايا العصبية إلى الطبقة المخفية وج) هناك أكثر من عنصر مخفي.
إثبات:1. الجزء الأصعب هو التحول الخطي. لجعل هذا ممكنًا ، نحتاج إلى W أن يكون له محدد إيجابي. فرضيتنا هي أنه لا يساوي الصفر ، ويمكننا قلب العلامة إذا كانت سلبية عن طريق تبديل خليتين عصبيتين خفيتين ، وبالتالي يمكننا أن نضمن أن المحدد إيجابي. مساحة المصفوفات المحددة الموجبة متصلة ، لذلك يوجد p: [0،1] → GLn ®5 بحيث p (0) = Id و p (1) = W. يمكننا الانتقال باستمرار من وظيفة الهوية إلى تحويل W باستخدام الوظائف x → p (t) x ، وضرب x في كل نقطة زمنية t في مصفوفة تمر باستمرار p (t).
2. يمكننا الانتقال باستمرار من وظيفة الهوية إلى الخريطة b باستخدام الوظيفة x → x + tb.
3. يمكننا الانتقال باستمرار من الوظيفة المتطابقة إلى الاستخدام النقطي لـ σ مع الوظيفة: x → (1-t) x + tσ (x)
حتى الآن ، من غير المرجح أن تظهر العلاقات التي تحدثنا عنها في البيانات الحقيقية ، ولكن هناك تعميمات على مستوى أعلى. من المعقول أن هذه الميزات قد تكون موجودة في بيانات حقيقية.
تعد الوصلات والعقد مشعبات أحادية البعد ، ولكننا نحتاج إلى 4 أبعاد حتى تتمكن الشبكات من كشفها جميعًا. وبالمثل ، قد تكون هناك حاجة إلى مساحة أبعاد أكبر حتى تتمكن من توسيع الفتحات ذات الأبعاد n. يمكن توسيع جميع المشعبات ذات الأبعاد n في أبعاد 2n + 2. [3]
خروج سهل
إن الطريقة السهلة هي محاولة فصل المشعبات عن بعضها وتمديد الأجزاء المتشابكة قدر الإمكان. على الرغم من أن هذا لن يكون قريبًا من حل حقيقي ، إلا أن هذا الحل يمكن أن يحقق دقة تصنيف عالية نسبيًا ويكون الحد الأدنى المحلي المقبول.

هذه الحدود الدنيا المحلية عديمة الفائدة على الإطلاق من حيث محاولة حل المشاكل الطوبوغرافية ، ولكن المشاكل الطوبولوجية يمكن أن توفر دافعًا جيدًا لدراسة هذه المشكلات.
من ناحية أخرى ، إذا كنا مهتمين فقط بتحقيق نتائج تصنيف جيدة ، فإن النهج مقبول. إذا تم التقاط جزء صغير جدًا من مشعب بيانات على مشعب آخر ، فهل هذه مشكلة؟ من المحتمل أنه سيكون من الممكن الحصول على نتائج تصنيف جيدة بشكل تعسفي ، على الرغم من هذه المشكلة.
طبقات محسنة لمعالجة المشعبات؟
من الصعب أن نتخيل أن الطبقات القياسية مع التحولات الأفينية جيدة حقًا للتعامل مع المشعبات.
ربما يكون من المنطقي أن يكون لدينا طبقة مختلفة تمامًا ، والتي يمكننا استخدامها في التكوين مع الطبقات التقليدية؟
إن دراسة مجال المتجه مع الاتجاه الذي نريد تغيير المشعب فيه واعدة:

ثم نقوم بتشويه الفضاء بناءً على حقل المتجه:
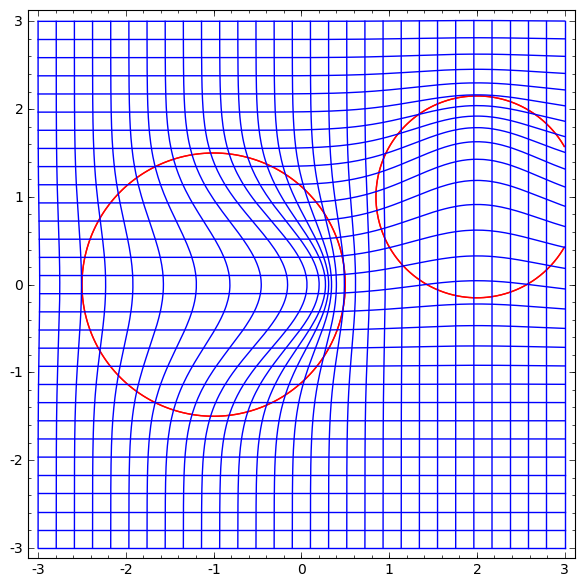
يمكن للمرء أن يدرس مجال المتجه عند نقاط ثابتة (فقط خذ بعض النقاط الثابتة من مجموعة بيانات الاختبار لاستخدامها كمثبتات) واستكمل بطريقة ما.
يحتوي حقل المتجه أعلاه على النموذج:P (x) = (v0f0 (x) + v1f1 (x)) / (1 + 0 (x) + f1 (x))
حيث v0 و v1 متجهان ، و f0 (x) و f1 (x) عبارة عن Gaussians ذات الأبعاد n.
K- أقرب طبقات الجوار
يمكن أن تكون قابلية الفصل الخطية حاجة ضخمة وربما غير معقولة للشبكات العصبية. من الطبيعي استخدام طريقة أقرب الجيران (k-NN). ومع ذلك ، فإن نجاح k-NN يعتمد بشكل كبير على العرض التقديمي الذي يصنفه ، لذا يلزم تقديم عرض جيد قبل أن تتمكن k-NN من العمل بشكل جيد.
يمكن تمييز k-NN فيما يتعلق بالتمثيل الذي تعمل عليه. بهذه الطريقة ، يمكننا تدريب الشبكة مباشرة لتصنيف k-NN. يمكن أن ينظر إلى هذا على أنه نوع من "الطبقة المجاورة" التي تعمل كبديل ل softmax.
لا نريد أن نحذر من مجموعتنا الكاملة من التدريب لكل حزب صغير ، لأنه سيكون إجراء مكلفًا للغاية. يتمثل النهج المتكيف في تصنيف كل عنصر في اللوت المصغر بناءً على فئات العناصر الأخرى في اللوت الصغير ، مع إعطاء كل وحدة وزن مقسومًا على المسافة من هدف التصنيف.
لسوء الحظ ، حتى مع البنى المعقدة ، فإن استخدام k-NN يقلل من احتمالية الخطأ - واستخدام البنى الأبسط يقلل من النتائج.
الخلاصة
يمكن للخصائص الطوبولوجية للبيانات ، مثل العلاقات ، أن تجعل التقسيم الخطي للفئات مستحيلًا باستخدام شبكات منخفضة الأبعاد ، بغض النظر عن العمق. حتى في الحالات التي يكون فيها ذلك ممكنًا من الناحية التقنية. على سبيل المثال ، اللوالب ، والتي قد يكون من الصعب للغاية فصلها.
لتصنيف البيانات الدقيق ، تحتاج الشبكات العصبية إلى طبقات واسعة. بالإضافة إلى ذلك ، فإن الطبقات التقليدية للشبكة العصبية غير مناسبة بشكل جيد لتمثيل التلاعبات المهمة مع المشعبات ؛ حتى لو قمنا بتعيين الأوزان يدويًا ، سيكون من الصعب تمثيل التحويلات التي نريدها بشكل مضغوط.
روابط للمصادر والتفسيرات[١] الكثير من التحولات الطبيعية التي قد ترغب في إجرائها على صورة ، مثل ترجمة أو تغيير حجم كائن بداخلها ، أو تغيير الإضاءة ، ستشكل منحنيات مستمرة في مساحة الصورة إذا كنت تقوم بها باستمرار.
[2] كارلسون وآخرون. وجدت أن البقع المحلية من الصور تشكل زجاجة كلاين.
[3] هذه النتيجة مذكورة في قسم ويكيبيديا الفرعي في إصدارات النظائر المشعة.