🧕🏻 👈🏾 🐣 صيغة Tupper وتنفيذ الخوارزمية في Python 🌆 🚫 👨🏾‍🤝‍👨🏻

بدلا من المقدمة

منذ وقت ليس ببعيد ، على الإنترنت ، تعلمت عن نسخة رائعة ومذهلة من المكتبة البابلية مثل صيغة تابر . بدلا من ذلك ، هو عدم المساواة Tupper أكثر من الصيغة. خصوصية هذا التفاوت هو أنه يخلق صورته الخاصة على الرسم البياني. مجرد إلقاء نظرة على هذه المعجزة!

(مصدر ويكيبيديا)

ما تراه في الصورة هو صيغة جيف تابر نفسه. ربما ذهب نصف القراء بالفعل إلى التنغستن لرسم نتيجة هذا التفاوت ... لكن هذا ليس بهذه البساطة. كما ترى في هذه الصورة ، يمكن رؤية الصيغة على الرسم البياني على مقطع على طول المحور OY [k؛ ك + 15]. ما هذا الرقم الغامض ك؟ من أين تحصل عليه؟ الشيء هو أن هذا التفاوت ، وفقًا لمفهوم المكتبة البابلية ، يمكنه عرض أي صورة بدقة تبلغ 106 × 17! كل صورة لها موقعها الخاص على الرسم البياني ، وبالتالي لديها رقم فريد ك. وهكذا ، لكل صورة ك هناك صورة واحدة على الرسم البياني بأكمله !

بالنسبة لصورة معينة ، يكون الرقم k على النحو التالي:

4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300

من المثير للاهتمام أن ننظر إلى الأشخاص الذين سينتقلون إلى مثل هذا الإحداثيات لرؤية الصيغة

حدث لي أن أكتب برنامجًا في Python3 من شأنه تحويل صورة إلى رقم k والعكس وإخبارك عن طريقة رائعة أخرى لترميز صورة إلى رقم.

النظرية

(مضاف) كيف يعمل؟

دعونا نلقي نظرة على الصيغة نفسها:
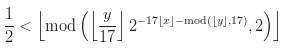
الصورة

دعونا نحدد تركيبها:
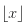
الصورة

- الرقم مقرب لأسفل
mod (x، y) - ما تبقى من قسمة x على y

ثم يبدو أن كل شيء واضح.
لاحظ أنه يتم تقريب كل من x و y. هذا التقريب هو الذي يعطينا في النهاية صورة بكسل
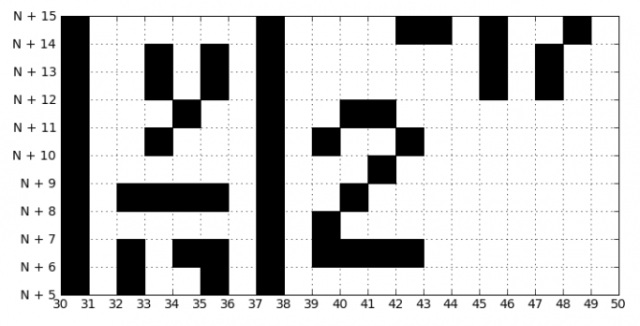
الصورة

تشير إلى كل ما يتم تقريبه على الجانب الأيمن من عدم المساواة

a l p h a

$\ alpha$ .
ثم

1 / 2 < [a l p h a] <=> 1 <= [a l p h a]

$1/2 <[\ alpha] <=> 1 <= [\ alpha]$

وهو أمر واضح ، لأن التعبير كله تقريب تقريبًا.

دع y = 17r + q ، حيث r هو الجزء الصحيح من قسمة y على 17 ، و r هو باقي القسمة. وبالتالي ، يمكننا استبدال الصيغة

[y / 17]

$[y / 17]$ على ص ، و

m o d (y ، 17)

$mod (y، 17)$ على ف.

نحصل

1 <= m o d (q * 2^{- 17 - r} ، 2)

$1 <= mod (q * 2 ^ {- 17-r}، 2)$

وإلا

1 <= m o d (q / 2^{17 x + r} ، 2)

$1 <= mod (q / 2 ^ {17x + r}، 2)$

وزارة الدفاع (

a l p h a

$\ alpha$ ، 2) يأخذ قيمتين - 0 أو 1. وبناءً على ذلك ، سيوضح هذا التفاوت ما إذا كان الرقم

q / 2^{17 x + r}

$q / 2 ^ {17x + r}$ حتى أم لا.

لاحظ أنه يتم عرض الصورة في الفاصل الزمني [N، N + 16] ، على التوالي

q = [y / 17]

$q = [y / 17]$ يبقى ثابتًا طوال ارتفاع الصورة بالكامل ، والذي لا يمكن قوله عن الرقم r (يختلف في الصورة بأكملها من 0 إلى 16).

والآن الكرز على الكعكة. رقم

[q / 2^{17 x + r}]

$[q / {2 ^ {17x + r}}]$ ستكون غريبة إذا وفقط إذا كان رقم البت (17x + r) في التمثيل الثنائي لـ q يساوي 1. وبما أن الرقم q يتغير باستمرار مع ارتفاعه وتمثيله الثنائي أيضًا ، فإننا نحصل على صورة فريدة في كل مرة! هذا هو بالضبط ما تعمل به صيغة تابر.

الآن دعونا نرى كيفية حساب الارتفاع الذي نريد أن نرى صورتنا فيه

مبدأ حساب العدد ك

وصف تابر نفسه حساب الرقم k لأي صورة 106x17 (هذا مهم!) على النحو التالي:

تحويل الصورة إلى أبيض وأسود
اقرأ كل بكسل من الأسفل إلى الأعلى ، من اليسار إلى اليمين وضعه في المخزن المؤقت. إذا كان بكسل الأسود - ثم ضع 1 ، إذا كان أبيض - 0.
تحويل ثنائي إلى عشري وضرب في 17
ربح!

للحصول على صورة من الرقم k ، نقوم بكل شيء عكس ذلك تمامًا. حسنا ، دعنا نذهب الترميز!

Kodim

حدث: في التعليقات ، قام الناس بتحسين الشفرة قليلاً ، وجعلها أبسط وأكثر شفافية. نشرت هذه المقالة بيانات التحديث. إذا كنت تريد أن ترى الإصدارات القديمة من الكود - اذهب إلى مستودع جيثب (حتى تلتزم به ، اربط في نهاية المقال) وفي التعليق

من ك إلى الصورة

UPD

بناء على طلب المعلقين ، تمت إضافة طريقة جديدة لحساب الصورة باستخدام هذا التفاوت و k! الآن لن نقوم بالتلاعب بالرقم ، وننتقل إلى النظام الثنائي ، ولكننا نؤثر بشكل مباشر على الوظيفة نفسها!

باستخدام طريقة المدقق لفك تشفير الرقم ك

نحصل على الرقم k من المستخدم ، ~~وعيناه مغلقتان~~ نقسمه على 17 ونترجمه إلى النظام الثنائي.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:]

نتفهم أن بعض وحدات البكسل الأولية يمكن أن تكون بيضاء (تساوي 0) ، على التوالي ، بالنسبة للرقم الثنائي لدينا ، ستكون البتات الأولى عبارة عن أصفار ، وعند ترجمة رقم إلى نظام عشري ، سيتم فقد هذه الأصفار الأولية. لذلك ، نتحقق من حجم الرقم الثنائي الناتج ، إذا كان أقل من 1802 ، ثم نضيف الأصفار إلى البداية.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] #   RadicalDreamer binary = ("0" * (1802 - len(binary))) + binary

بعد ذلك ، أعلن عن قائمة ثنائية الأبعاد نقوم فيها بتخزين معلومات حول كل سطر من الصورة. ثم نكتب كل تلك البتات التي نقرأها (لا تنس الخوارزمية التي يتم بها إنشاء الرقم k - من الأسفل إلى الأعلى ، من اليسار إلى اليمين)

 lists = [[] for x in range(17)] #C   RadicalDreamer for x in range(1802): lists[-(x % 17)].append(binary[x]) <b> !</b> <source lang="python"> #-----!-----# image = Image.new("1", (106,17), (0)) # -  10617 draw = image.load() for y in range(17): for x in range(106): image.putpixel(xy=(105-x,16-y), value=(int(lists[y][x]),)) #    ,      lists image.save("image.png") #

دعونا نحاول دفع الرقم k ، الذي أشرت إليه في بداية المقالة ، في برنامجنا والحصول على ما يلي:

الصورة

كما ترى ، نجح كل شيء بالنسبة لنا ، ونحن الآن قادرون على فك أي ك!

استخدام اللامساواة لتوليد صورة من ك

أولاً ، اكتب الوظيفة في بايثون:

 def f(x,y): return ((y//17)//(1 << (17*x+(y%17))))%2

بفضل عوامل التشغيل // و << ، تم تبسيط تنفيذ الوظيفة بشكل كبير. من المؤكد أن الأعداد x و y ستكون أعدادا صحيحة !

ننشئ مرة أخرى قائمة ثنائية الأبعاد ، حيث سنقوم بتخزين أجزاء الصورة ونكتب معلومات حول كل سطر فيها باستخدام حلقات

 lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2))

ثم ، كما في المثال السابق ، نرسم صورة باستخدام مكتبة PIL.

تبدو الوظيفة الكاملة كما يلي:

 def from_k_to_bin(k: int) -> list: lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) return lists

صورة في ك

حسنًا ، سنتعلم الآن ترميز أي صورة في الرقم ك.

أولاً نحصل على الصورة نفسها

 def get_image() -> Image: name = input("   (      ):") try: im = Image.open(name) except Exception: print("!") exit(0) return im

تحقق من حجمه

 _SIZE_WIDTH = 106 _SIZE_HEIGHT = 17 image = get_image() width, height = image.size flag_okay = False if width == _SIZE_WIDTH and height == _SIZE_HEIGHT: flag_okay = True if not flag_okay: print("  ") print(width, height) exit(0) print(" !")

نصنع الصورة بالأبيض والأسود ونبدأ في قراءة البكسل بالبكسل:

 image = image.convert('1') byteset = "" for x in range(105,-1,-1): for y in range(0,17): #c m03r   if image.getpixel((x,y)) > 127: byteset += '1' else: byteset += '0'

يبقى فقط للتحويل إلى النظام العشري وضربه في 17.

 k = int(byteset,2)*17 print(" :") print(k)

حسنا ، دعنا نذهب الاختبار!

قررت ترميز شعار الهبر. ها هي صورة المصدر:

نبدأ البرنامج ونحدد اسم الصورة:

حصلنا على ك التالية:

4858487703217654168507377107565676789145697178497253677539145555247620343537955749299116772611982962556356527603203744742682135448820545638134012705381689785851604674225344958377377969928942310236199337805399065932982909660659786056259547094494380793146587709009524498386724160055692719747815828234655968636671461350354316223620304956111171025410498514602810746287134775641383930152393933036921599511277388743068766568352667661462097979110006690900253037600818522726237351439443865433159187625289316917268254866954663750093103703327097252478959

دعونا نتحقق من ذلك في برنامجنا الخاص.

هذه هي الصورة التي تلقيناها:

كانت مشوهة قليلاً بسبب ترجمة ملتوية قليلاً للصورة بالأبيض والأسود.

الملخص

كود المصدر: جيثب

المصادر: مقالة ويكي

صيغة Tupper وتنفيذ الخوارزمية في Python