تحية للجميع ، وخاصة أولئك الذين يرغبون في الرياضيات المنفصلة ونظرية الرسم البياني.
الخلفية
حدث ذلك أنني ، مدفوعة بالاهتمام ، كنت أقوم بتطوير خدمة بناء جولة. الطرق. كانت المهمة هي تخطيط أفضل الطرق استنادًا إلى المدينة التي تهم المستخدم وفئات المؤسسات والإطار الزمني. حسنًا ، كانت إحدى المهام الفرعية حساب وقت السفر من مؤسسة إلى أخرى. منذ أن كنت شابًا وغبيًا ، قمت بحل هذه المشكلة مباشرةً ، باستخدام خوارزمية ديكسترا ، ولكن من العدل أن نلاحظ أنه فقط من خلاله كان من الممكن بدء التكرار من عقدة لآلاف آخرين ، لم يكن التخزين المؤقت لهذه المسافات خيارًا ، المؤسسات أكثر من 10 آلاف فقط موسكو وحدها ، وقرارات مثل المسافة مانهاتن في مدننا لا تعمل من الكلمة على الإطلاق.
وهكذا اتضح أنه كان من الممكن حل مشكلة الأداء في مشكلة التوافقية ، ولكن معظم الوقت لمعالجة الطلب تم إنفاقه على البحث عن المسارات غير المخزنة مؤقتًا. كانت المشكلة معقدة بسبب حقيقة أن الرسم البياني للطريق Osm في موسكو كبير جدًا (نصف مليون عقد و 1.1 مليون قوس).
لن أتحدث عن كل المحاولات وأنه في الواقع يمكن حل المشكلة عن طريق قطع الأقواس الإضافية للرسم البياني ، سأخبرك فقط أنه في مرحلة ما فجر علي وأدركت أنه إذا اقتربت من خوارزمية ديكسترا من حيث النهج الاحتمالي ، يمكن أن تكون خطية.
Dijkstra لوقت لوغاريتمي
يعلم الجميع ، ولكن من يدري ، أن خوارزمية Dijkstra باستخدام قائمة انتظار مع التعقيد اللوغاريتمي للإدراج والحذف يمكن أن يؤدي إلى تعقيد النموذج O (n log (n) + m log (n)). عند استخدام كومة فيبوناتشي ، يمكن تقليل التعقيد إلى O (n * log (n) + m) ، ولكن لا يزال غير خطي ، لكني أرغب في ذلك.
في الحالة العامة ، يتم وصف خوارزمية قائمة الانتظار على النحو التالي:
دع:
- V هي مجموعة رؤوس الرسم البياني
- E هي مجموعة حواف الرسم البياني
- w [i، j] هو وزن الحافة من العقدة i إلى العقدة j
- أ - بدء قمة البحث
- قائمة انتظار q-vertex
- d [i] - المسافة إلى العقدة i
- d [a] = 0 ، لجميع d [i] = + inf الأخرى
في حين أن q ليست فارغة:
- v هي قمة الحد الأدنى d [v] من q
- بالنسبة لجميع القمم التي يوجد بها انتقال إلى E من القمة v
- إذا d [u]> w [vu] + d [v]
- احذف u من q بمسافة d [u]
- d [u] = w [vu] + d [v]
- أضف u إلى q بالمسافة d [u]
- إزالة الخامس من ف
إذا استخدمنا شجرة حمراء سوداء كقائمة انتظار ، حيث يحدث الإدراج والحذف في السجل (n) ، ويكون البحث عن العنصر الأدنى مشابهًا في السجل (ن) ، فإن تعقيد الخوارزمية هو O (n log (n) + m log (n)) .
وهنا تجدر الإشارة إلى ميزة واحدة مهمة: لا شيء يمنع ، من الناحية النظرية ، النظر في القمة عدة مرات. إذا تم فحص قمة الرأس وتم تحديث المسافة إليه إلى قيمة غير صحيحة ، أكبر من القيمة الحقيقية ، ثم ، بشرط أن يتقارب النظام عاجلاً أم آجلاً ويتم تحديث المسافة إلى u إلى القيمة الصحيحة ، يجوز إجراء مثل هذه الحيل. ولكن من الجدير بالذكر - يجب اعتبار رأس واحد أكثر من مرة واحدة مع احتمال ضعيف.
فرز جدول التجزئة
لتقليل وقت تشغيل خوارزمية Dijkstra إلى خطية ، يتم اقتراح بنية بيانات ، وهي عبارة عن جدول تجزئة مع أرقام عقدة (node_id) كقيم. ألاحظ أن الحاجة إلى الصفيف d لا تختفي ، لا تزال هناك حاجة للحصول على المسافة إلى العقدة ith في وقت ثابت.
يوضح الشكل أدناه مثالاً على الهيكل المقترح.
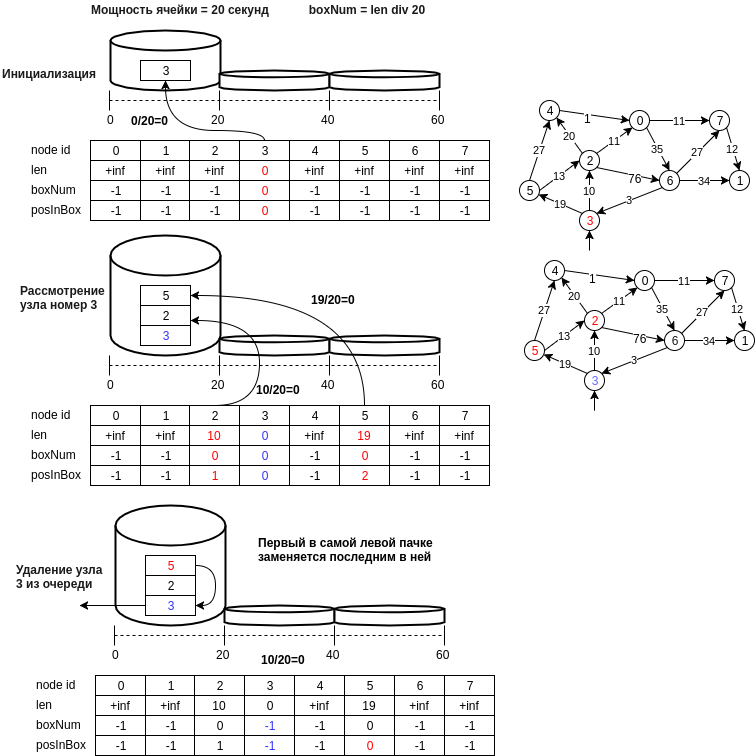
دعنا نصف خطوات هيكل البيانات المقترح:
- العقدة u مكتوبة في الخلية برقم يساوي d [u] // bucket_size ، حيث bucket_size هي قوة الخلية (على سبيل المثال ، 20 مترًا ، أي أن الخلية في الرقم 0 ستحتوي على عقد المسافة التي تقع في النطاق [0 ، 20) متر )
- العقدة الأخيرة للخلية الأولى غير الفارغة ، أي سيتم تنفيذ عملية استخراج الحد الأدنى من العنصر في O (1). من الضروري الحفاظ على الحالة الحالية لمعرف رقم الخلية الأولى غير الفارغة (min_el).
- تتم عملية الإدراج عن طريق إضافة رقم عقدة جديد إلى نهاية الخلية وتنفيذ O (1) أيضًا ، لأن يحدث حساب رقم الخلية في وقت ثابت.
- عملية الحذف ، كما هو الحال في جدول التجزئة ، من الممكن العد الطبيعي ، ويمكن للمرء أن يفترض ويقول أن حجم الخلية الصغير هو أيضًا O (1). إذا كنت لا تمانع في الذاكرة (من حيث المبدأ ، وليس هناك حاجة كبيرة ، صفيف آخر من قبل ن) ، ثم يمكنك إنشاء مجموعة من المواضع في الخلية. في هذه الحالة ، إذا تم حذف العنصر في منتصف الخلية ، فمن الضروري نقل القيمة الأخيرة في الخلية إلى الموقع المحذوف.
- نقطة مهمة عند اختيار الحد الأدنى للعنصر: هو الحد الأدنى فقط مع بعض الاحتمالية ، ولكن ، ستنظر الخوارزمية في الخلية min_el حتى تصبح فارغة ، وسيتم النظر في الحد الأدنى الحقيقي للعنصر ، عاجلاً أم آجلاً ، وإذا قمنا عن طريق الخطأ بتحديث قيمة المسافة إلى العقدة التي يمكن الوصول إليها من الحد الأدنى ، ثم يمكن أن تكون العقد المجاورة للحد الأدنى مرة أخرى في قائمة الانتظار وستكون المسافة بينها صحيحة ، وما إلى ذلك.
- يمكنك أيضًا حذف الخلايا الفارغة حتى min_el ، مما يوفر الذاكرة. في هذه الحالة ، يجب إزالة العقدة v من قائمة الانتظار q فقط بعد النظر في جميع العقد المجاورة.
- ويمكنك أيضًا تغيير طاقة الخلية والمعلمات لزيادة حجم الخلية وعدد الخلايا عندما تحتاج إلى زيادة حجم جدول التجزئة.
نتائج القياس
تم إجراء الشيكات على خريطة osm لموسكو ، وتفريغها عبر osm2po في postgres ، ثم تحميلها في الذاكرة. تمت كتابة الاختبارات بلغة جافا. كان هناك 3 إصدارات من الرسم البياني:
- الرسم البياني المصدر - 0.43 مليون عقدة ، 1.14 مليون عقد
- نسخة مضغوطة من الرسم البياني مع عقد 173k وأقواس 750k
- نسخة المشاة من النسخة المضغوطة من الرسم البياني ، أقواس 450k ، عقد 100k.
فيما يلي صورة بقياسات على إصدارات مختلفة من الرسم البياني:

خذ بعين الاعتبار اعتماد احتمال إعادة عرض قمة وحجم الرسم البياني:
| عدد مشاهدات العقدة | عد القمم | احتمالية إعادة عرض العقدة |
|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0.9 |
| 431490 | 419594 | 2.8 |
قد تلاحظ أن الاحتمالية لا تعتمد على حجم الرسم البياني وهي محددة إلى حد ما للطلب ، ولكنها صغيرة ويتم تكوين نطاقها عن طريق تغيير قوة الخلية. سأكون ممتنًا جدًا للمساعدة في إنشاء تعديل احتمالي للخوارزمية مع معلمات تضمن فترة ثقة ضمن النطاق الذي لن يتجاوز احتمال المشاهدة المتكررة نسبة معينة.
كما تم إجراء قياسات نوعية للتأكيد عمليًا على مقارنة صحة نتيجة الخوارزميات مع بنية البيانات الجديدة ، والتي أظهرت مصادفة كاملة لأقصر طول للمسار من 1000 عقد عشوائية إلى 1000 عقد عشوائية أخرى على الرسم البياني. (وهكذا 250 تكرارًا) عند العمل مع جدول تجزئة الفرز وشجرة حمراء-سوداء.
يوجد الكود المصدر لهيكل البيانات المقترح على الرابط
ملاحظة: أعرف عن خوارزمية Torup وحقيقة أنها تحل نفس المشكلة في الوقت الخطي ، لكنني لم أستطع إتقان هذا العمل الأساسي في إحدى الليالي ، على الرغم من أنني فهمت الفكرة بعبارات عامة. على الأقل ، كما أفهمها ، يتم اقتراح نهج آخر هناك ، بناءً على بناء شجرة ممتدة دنيا.
PSS في غضون أسبوع سأحاول العثور على الوقت وإجراء مقارنة مع مجموعة فيبوناتشي وبعد ذلك بقليل أضف اللفت جيثب مع أمثلة ورموز اختبار.