في مجال التعرف على الانفعالات ، يعد الصوت ثاني أهم مصدر للبيانات العاطفية بعد الوجه. يمكن تمييز الصوت بعدة معايير. يعد الصوت الصوتي أحد الخصائص الرئيسية من هذا القبيل ، ومع ذلك ، في مجال التكنولوجيا الصوتية ، من الأصح استدعاء هذه المعلمة التردد الأساسي.
يرتبط تكرار النغمة الأساسية مباشرة بما نسميه التجويد. ويرتبط التجويد ، على سبيل المثال ، بالخصائص العاطفية للتعبير عن الصوت.
ومع ذلك ، فإن تحديد وتيرة النغمة الأساسية ليست مهمة تافهة تمامًا مع فروق دقيقة مثيرة للاهتمام. في هذه المقالة ، سنناقش ميزات الخوارزميات لتحديدها ومقارنة الحلول الحالية مع أمثلة من تسجيلات صوتية محددة.
مقدمةبادئ ذي بدء ، دعونا نتذكر ما هو في جوهره تردد النغمة الأساسية والمهام التي قد تكون مطلوبة.
التردد الأساسي ، الذي يشار إليه أيضًا باسم CHOT أو التردد الأساسي أو F0 ، هو تردد الحبال الصوتية عند نطق الأصوات الصوتية. عند نطق الأصوات غير النغمة (التي لم يتم التحقق منها) ، على سبيل المثال ، التحدث بصوت همس أو نطق أصوات الصفير والصفير ، لا تتردد الأربطة ، مما يعني أن هذه الخاصية ليست ذات صلة بها.
* يرجى ملاحظة أن التقسيم إلى أصوات نغمية وغير نغمية لا يعادل الانقسام إلى حروف العلة والحروف الساكنة.
إن تنوع تردد النغمة الأساسية كبير جدًا ، ويمكن أن يختلف اختلافًا كبيرًا ليس فقط بين الأشخاص (بالنسبة لأصوات الذكور الأقل متوسطًا ، يكون التردد 70-200 هرتز ، وللأصوات الإناث يمكن أن يصل إلى 400 هرتز) ، ولكن أيضًا لشخص واحد ، خاصة في الكلام العاطفي .
يتم استخدام تحديد تواتر النغمة الأساسية لحل مجموعة واسعة من المشاكل:
- الاعتراف بالعواطف ، كما قلنا أعلاه ؛
- تحديد الجنس ؛
- عند حل مشكلة تقسيم الصوت بأصوات متعددة أو تقسيم الكلام إلى عبارات ؛
- في الطب ، لتحديد الخصائص المرضية للصوت (على سبيل المثال ، باستخدام المعلمات الصوتية Jitter and Shimmer). على سبيل المثال ، تحديد علامات مرض باركنسون [ 1 ]. يمكن أيضًا استخدام Jitter و Shimmer للتعرف على العواطف [ 2 ].
ومع ذلك ، هناك عدد من الصعوبات في تحديد F0. على سبيل المثال ، غالبًا ما يكون من الممكن الخلط بين F0 والتوافقيات ، والتي يمكن أن تؤدي إلى ما يسمى بتأثيرات مضاعفة الملعب / تقليل الملعب إلى النصف [
3 ]. وفي التسجيلات الصوتية ذات الجودة الرديئة ، من الصعب جدًا حساب F0 ، نظرًا لأن الذروة المطلوبة عند الترددات المنخفضة تختفي تقريبًا.
بالمناسبة ، تذكر قصة
لوريل وياني ؟ نشأت الاختلافات في الكلمات التي يسمعها الناس عند الاستماع إلى نفس التسجيل الصوتي ، على وجه التحديد بسبب الاختلاف في الإدراك F0 ، والذي يتأثر بعدة عوامل: عمر المستمع ، ودرجة التعب ، وجهاز التشغيل. لذلك ، عند الاستماع إلى التسجيلات في مكبرات الصوت مع إعادة إنتاج عالية الجودة للترددات المنخفضة ، ستسمع لوريل ، وفي الأنظمة الصوتية حيث يتم إنتاج الترددات المنخفضة بشكل سيئ ، ياني. يمكن رؤية تأثير الانتقال على جهاز واحد ، على سبيل المثال
هنا . وفي هذه
المقالة ، تعمل الشبكة العصبية كمستمع. في
مقال آخر
، يمكنك قراءة كيفية شرح ظاهرة Yanny / Laurel من حيث تكوين الكلام.
نظرًا لأن التحليل التفصيلي لجميع طرق تحديد F0 سيكون ضخمًا جدًا ، فإن المقالة ذات طبيعة عامة ويمكن أن تساعد في التنقل في الموضوع.
طرق تحديد F0يمكن تقسيم طرق تحديد F0 إلى ثلاث فئات: استنادًا إلى ديناميكيات الوقت للإشارة أو المجال الزمني ؛ بناءً على بنية التردد ، أو مجال التردد ، بالإضافة إلى الطرق المجمعة. نقترح أن تتعرف على
مقالة المراجعة حول الموضوع ، حيث يتم تحليل الطرق المشار إليها لاستخراج F0 بالتفصيل.
لاحظ أن أي من الخوارزميات التي تمت مناقشتها تتكون من 3 خطوات رئيسية:
المعالجة المسبقة (تصفية الإشارة وتقسيمها إلى إطارات)
البحث عن القيم المحتملة لـ F0 (المرشحين)
التتبع هو اختيار المسار الأكثر احتمالا F0 (لأنه في كل لحظة من الزمن لدينا العديد من المرشحين المتنافسين ، نحتاج إلى العثور على المسار الأكثر احتمالا بينهم)
المجال الزمنينوجز بعض النقاط العامة. قبل تطبيق أساليب المجال الزمني ، يتم تصفية الإشارة مسبقًا ، تاركة الترددات المنخفضة فقط. يتم تعيين العتبات - الحد الأدنى والحد الأقصى للترددات ، على سبيل المثال من 75 إلى 500 هرتز. يتم تحديد F0 فقط للمناطق ذات الكلام التوافقي ، نظرًا لأن التوقف المؤقت أو أصوات الضجيج لا يعني ذلك فقط ، بل يمكن أيضًا تقديم أخطاء في الإطارات المجاورة عند تطبيق الاستيفاء و / أو التنعيم. يتم تحديد طول الإطار بحيث يحتوي على ثلاث فترات على الأقل.
الطريقة الرئيسية ، التي ظهرت على أساسها عائلة كاملة من الخوارزميات في وقت لاحق ، هي الترابط الذاتي. النهج بسيط للغاية - من الضروري حساب وظيفة الترابط الذاتي وأخذ الحد الأقصى الأول. سيعرض مكون التردد الأكثر وضوحًا في الإشارة. ماذا يمكن أن تكون الصعوبة في حالة استخدام الترابط الذاتي ولماذا هو أبعد ما يكون عن أن الحد الأقصى الأول سوف يتوافق مع التردد المطلوب؟ حتى بالقرب من الظروف المثالية للتسجيلات عالية الجودة ، قد تكون الطريقة خاطئة بسبب البنية المعقدة للإشارة. في الظروف القريبة من الواقع ، حيث قد نواجه ، من بين أمور أخرى ، اختفاء الذروة المطلوبة في التسجيلات الصاخبة أو التسجيلات ذات الجودة المنخفضة في البداية ، يزداد عدد الأخطاء بشكل حاد.
على الرغم من الأخطاء ، فإن طريقة الارتباط الذاتي مريحة وجذابة تمامًا نظرًا لبساطتها ومنطقها الأساسي ، ولهذا السبب يتم اعتبارها أساسًا في العديد من الخوارزميات ، بما في ذلك YIN. يشير حتى اسم الخوارزمية إلى التوازن بين الراحة وعدم الدقة في طريقة الارتباط الذاتي: "يشير اسم YIN من" yin "و" yang "للفلسفة الشرقية إلى التفاعل بين الترابط الذاتي والإلغاء الذي تنطوي عليه." [
4 ]
حاول مبدعو YIN إصلاح نقاط الضعف في نهج الارتباط الذاتي. التغيير الأول هو استخدام الدالة التراكمية لمتوسط الاختلاف الطبيعي ، والتي يجب أن تقلل من حساسية تعديلات السعة ، تجعل القمم أكثر وضوحًا:
\ تبدأ {المعادلة}
d'_t (\ tau) =
\ تبدأ {الحالات}
1 ، & \ tau = 0 \\
d_t (\ tau) \ bigg / \ bigg [\ frac {1} {\ tau} \ sum \ limits_ {j = 1} ^ {\ tau} d_t (j) \ bigg] و \ text {خلاف ذلك}
\ تنتهي {الحالات}
\ إنهاء {المعادلة}
تحاول YIN أيضًا تجنب الأخطاء التي تحدث في الحالات التي لا يكون فيها طول وظيفة النافذة مقسومًا بالكامل على فترة التذبذب. لهذا ، يتم استخدام الحد الأدنى من الاستيفاء المكافئ. في الخطوة الأخيرة من معالجة الإشارات الصوتية ، يتم تنفيذ أفضل وظيفة تقدير محلية لمنع القفزات الحادة في القيم (سواء كانت جيدة أو سيئة - هذه نقطة خلافية).
مجال الترددإذا تحدثنا عن مجال التردد ، فإن البنية التوافقية للإشارة تبرز في المقدمة ، أي وجود قمم طيفية عند ترددات مضاعفات F0. يمكنك "طي" هذا النمط الدوري إلى ذروة واضحة باستخدام تحليل cepstral. Cepstrum - تحويل فورييه لوغاريتم طيف الطاقة ؛ تتوافق ذروة cepstral مع أكثر المكونات الدورية للطيف (يمكن للمرء أن يقرأ عنها
هنا وهنا ).
طرق هجينة لتحديد F0الخوارزمية التالية ، التي تستحق استكشافها بمزيد من التفصيل ، تحمل اسم التحدث YAAPT - ومع ذلك خوارزمية أخرى لتتبع الانحدار - وهي في الواقع مختلطة ، لأنها تستخدم معلومات التردد والوقت. يوجد وصف كامل في
المقالة ، هنا نصف المراحل الرئيسية فقط.
الشكل 1. الرسم البياني خوارزمية YAAPTalgo ( حلقة الوصل ) .
يتكون YAAPT من عدة خطوات رئيسية ، أولها المعالجة المسبقة. في هذه المرحلة ، يتم تربيع قيم الإشارة الأصلية ، ويتم الحصول على نسخة ثانية من الإشارة. تسعى هذه الخطوة إلى تحقيق نفس الهدف مثل دالة التفاضل المتوسط الطبيعي التراكمي في YIN - تضخيم واستعادة القمم "المحشورة" من الارتباط الذاتي. يتم ترشيح كلا الإصدارين من الإشارة - عادة ما يأخذون نطاق 50-1500 هرتز ، وأحيانًا 50-900 هرتز.
ثم يحسب المسار الأساسي F0 من طيف الإشارة المحولة. يتم تحديد المرشحين لـ F0 باستخدام ميزة الارتباط التوافقي الطيفي (SHC).
\ تبدأ {المعادلة}
SHC (t، f) = \ sum \ limits_ {f '= - WL / 2} ^ {WL / 2} \ prod \ limits_ {r = 1} ^ {NH + 1} S (t، rf + f')
\ إنهاء {المعادلة}
حيث S (t، f) هو طيف الحجم للإطار t والتردد f ، WL هو طول النافذة في Hz ، NH هو عدد التوافقيات (يوصي المؤلفون باستخدام التوافقيات الثلاثة الأولى). تُستخدم القوة الطيفية أيضًا لتحديد الإطارات التي لم يتم تحرير فواتير بها ، وبعد ذلك يتم البحث عن المسار الأمثل ، ويؤخذ في الاعتبار إمكانية مضاعفة الملعب / النصف إلى الملعب [
3 ، القسم الثاني ، ج].
علاوة على ذلك ، يتم تحديد المرشحين لـ F0 لكل من الإشارة الأولية والإشارة المحولة ، وبدلاً من وظيفة الارتباط الذاتي ، يتم استخدام الارتباط المتبادل العادي (NCCF) هنا.
\ تبدأ {المعادلة}
NCCF (m) = \ frac {\ sum \ limits_ {n = 0} ^ {Nm-1} x (n) * x (n + m)} {\ sqrt {\ sum \ limits_ {n = 0} ^ { Nm-1} x ^ 2 (n) * \ sum \ limits_ {n = 0} ^ {Nm-1} x ^ 2 (n + m)}} \ text {،} \ hspace {0.3cm} 0 <m <M_ {0}
\ إنهاء {المعادلة}
الخطوة التالية هي تقييم جميع المرشحين المحتملين وحساب أهميتهم أو وزنهم (الجدارة). لا يعتمد وزن المرشحين المتحصل عليهم من الإشارة الصوتية على اتساع ذروة NCCF فحسب ، بل يعتمد أيضًا على قربهم من المسار F0 المحدد من الطيف. أي أن مجال التردد يعتبر خشنًا من حيث الدقة ، ولكنه مستقر [
3 ، القسم الثاني ، د].
ثم ، بالنسبة لجميع أزواج المرشحين المتبقين ، يتم حساب مصفوفة تكلفة الانتقال - سعر الانتقال ، حيث يجدون في النهاية المسار الأمثل [
3 ، القسم الثاني ، هـ].
أمثلةالآن نطبق جميع الخوارزميات المذكورة أعلاه على تسجيلات صوتية محددة. كنقطة انطلاق ، سوف نستخدم
Praat ، وهي أداة أساسية لكثير من علماء الكلام. ثم في Python سننظر في تنفيذ YIN و YAAPT وسنقوم بمقارنة النتائج المستلمة.
كمواد صوتية ، يمكنك استخدام أي صوت متاح. أخذنا عدة مقتطفات من قاعدة بيانات
RAMAS الخاصة بنا -
مجموعة بيانات متعددة الوسائط تم إنشاؤها بمشاركة ممثلي VGIK. يمكنك أيضًا استخدام مواد من قواعد بيانات مفتوحة أخرى ، مثل
LibriSpeech أو
RAVDESS .
كمثال توضيحي ، أخذنا مقتطفات من عدة تسجيلات بأصوات من الذكور والإناث ، محايدة وملونة عاطفية ، وللتوضيح ، قمنا بدمجها في
تسجيل واحد. دعونا نلقي نظرة على إشارتنا ، مطيافها ، شدتها (اللون البرتقالي) ، و F0 (اللون الأزرق). في Praat ، يمكن القيام بذلك باستخدام Ctrl + O (فتح - قراءة من الملف) ثم الزر عرض وتحرير.
الشكل 2. الشكل الطيفي ، كثافة (اللون البرتقالي) ، F0 (اللون الأزرق) في برات.يظهر الصوت بوضوح تام أنه في الكلام العاطفي ، تزداد حدة الصوت لدى كل من الرجال والنساء. في الوقت نفسه ، يمكن مقارنة F0 للكلام العاطفي للذكور مع F0 لصوت الأنثى.
تتبعحدد علامة التبويب تحليل دورية - إلى خطوة (ac) في قائمة Praat ، أي تعريف F0 باستخدام الارتباط التلقائي. ستظهر نافذة لتعيين المعلمات حيث يمكن تعيين 3 معلمات لتحديد المرشحين لـ F0 و 6 معلمات أخرى لخوارزمية مكتشف المسار ، والتي تبني المسار الأكثر احتمالا F0 بين جميع المرشحين.
العديد من المعلمات (في Praat ، يوجد وصفها أيضًا على زر المساعدة)- عتبة الصمت - عتبة السعة النسبية للإشارة لتحديد الصمت ، القيمة القياسية هي 0.03.
- حد الصوت - وزن المرشح الذي لم يتم تحرير فاتورة به ، القيمة القصوى هي 1. كلما زادت هذه المعلمة ، سيتم تعريف المزيد من الإطارات على أنها لم يتم التحقق منها ، أي أنها لا تحتوي على أصوات نغمات. في هذه الإطارات ، لن يتم تحديد F0. قيمة هذه المعلمة هي عتبة قمم وظيفة الارتباط الذاتي. القيمة الافتراضية هي 0.45.
- تكلفة Octave - تحدد مقدار الوزن الذي يتمتع به المرشحون ذوو التردد العالي بالنسبة إلى الترددات المنخفضة. كلما زادت القيمة ، زاد التفضيل للمرشح عالي التردد. القيمة الافتراضية هي 0.01 لكل أوكتاف.
- تكلفة قفزة الأوكتاف - مع زيادة هذا المعامل ، ينخفض عدد التحولات الشبيهة بالقفزة الحادة بين القيم المتتالية لـ F0. القيمة الافتراضية هي 0.35.
- التكلفة المعبر عنها / غير المحررة - زيادة هذا المعامل يقلل عدد التحولات المعبر عنها / غير المحررة. القيمة الافتراضية هي 0.14.
- سقف الملعب (هرتز) - لا تعتبر المرشحين فوق هذا التردد. القيمة الافتراضية هي 600 هرتز.
يمكن العثور على وصف تفصيلي للخوارزمية في
مقالة عام 1993.
يمكن رؤية ما تبدو عليه نتيجة أداة التتبع (أداة البحث عن المسار) بالنقر فوق موافق ثم عرض ملف العرض الناتج (عرض وتحرير). يمكن ملاحظة أنه بالإضافة إلى المسار المحدد ، كان لا يزال هناك مرشحين مهمين جدًا مع تردد أقل.
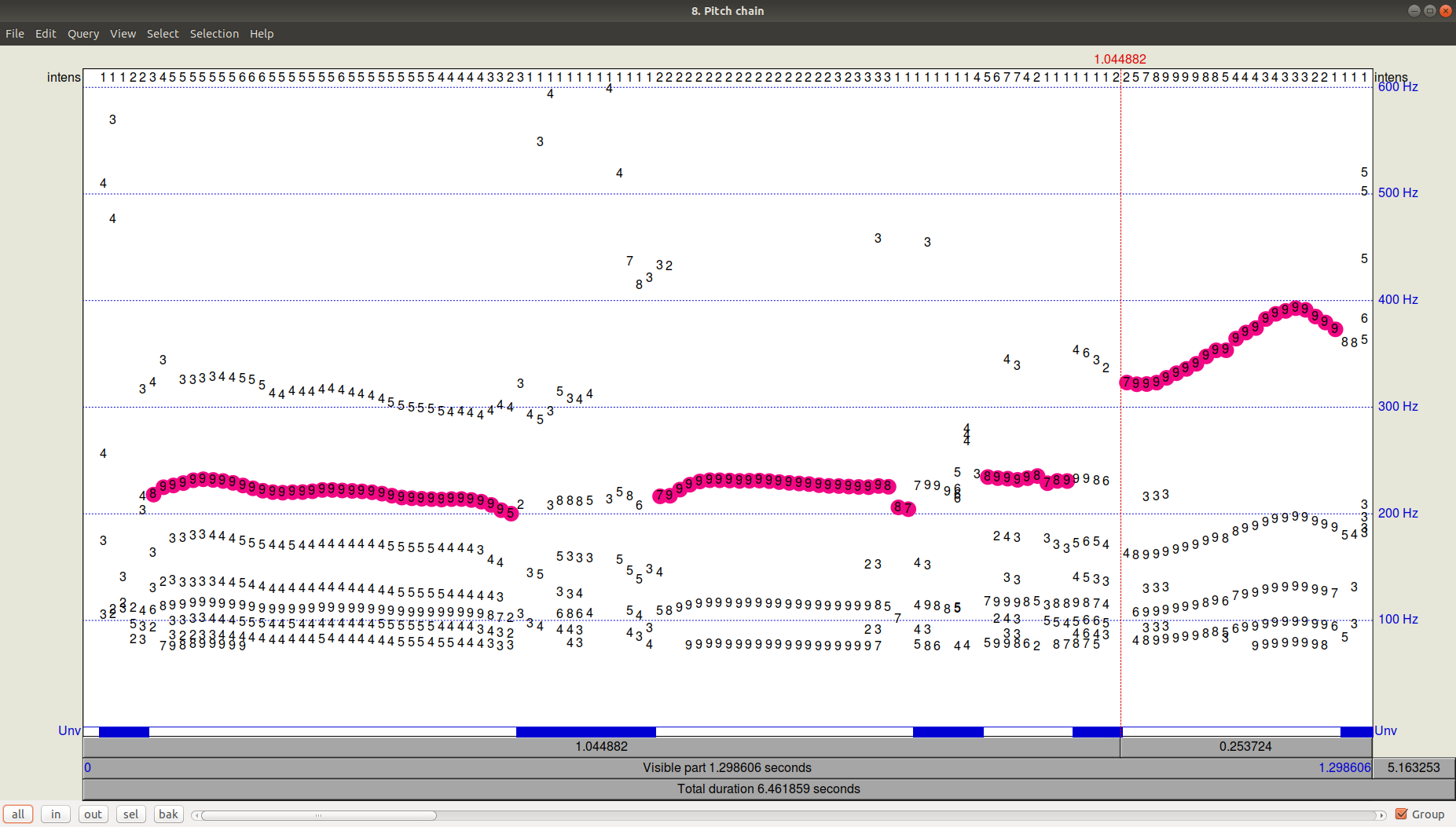الشكل 3. PitchPath لأول 1.3 ثانية من التسجيل الصوتي.لكن ماذا عن بايثون؟لنأخذ مكتبتين تقدمان تتبع
المسار -
aubio ، حيث تكون الخوارزمية الافتراضية هي YIN ، ومكتبة
AMFM_decompsition ، التي لديها تطبيق خوارزمية YAAPT. في الملف المنفصل (ملف
PraatPitch.txt ) ،
قم بإدراج قيم F0 من Praat (يمكن القيام بذلك يدويًا: حدد ملف الصوت ، وانقر فوق عرض وتحرير ، وحدد الملف بأكمله وحدد قائمة خطوة الملعب في القائمة العلوية).
قارن الآن نتائج الخوارزميات الثلاثة (YIN ، YAAPT ، Praat).
الكثير من التعليمات البرمجيةimport amfm_decompy.basic_tools as basic import amfm_decompy.pYAAPT as pYAAPT import matplotlib.pyplot as plt import numpy as np import sys from aubio import source, pitch
الشكل 4. مقارنة بين تشغيل خوارزميات YIN و YAAPT و Praat.نرى أنه مع المعلمات الافتراضية ، تم إيقاف YIN تمامًا ، وحصل على مسار مسطح للغاية بقيم أقل من Praat وفقد تمامًا التحولات بين أصوات الذكور والإناث ، وكذلك بين الكلام العاطفي وغير العاطفي.
خفضت YAAPT نغمة عالية جدًا في الكلام الأنثوي العاطفي ، لكن بشكل عام تمكنت بشكل أفضل. نظرًا لميزاته الخاصة ، يعمل YAAPT بشكل أفضل - من المستحيل الإجابة على الفور ، بالطبع ، ولكن يمكن افتراض أن الدور يتم لعبه من خلال الحصول على مرشحين من ثلاثة مصادر وحساب أكثر دقة لوزنهم مما هو عليه في YIN.
الخلاصةنظرًا لأن مسألة تحديد وتيرة النغمة الأساسية (F0) بشكل أو بآخر تنشأ قبل أن يعمل كل شخص تقريبًا مع الصوت ، فهناك العديد من الطرق لحلها. يحدد سؤال الدقة والميزات اللازمة للمادة الصوتية في كل حالة مدى الدقة في تحديد المعلمات ، أو في حالة أخرى ، يمكنك تقييد نفسك بحل أساسي مثل YAAPT. مع الأخذ في الاعتبار Praat كمعيار للخوارزمية لمعالجة الكلام (ومع ذلك ، يستخدمه عدد كبير من الباحثين) ، يمكننا أن نستنتج أن YAAPT ، إلى أول تقدير ، أكثر موثوقية ودقة من YIN ، على الرغم من أن مثالنا تبين أنه معقد لذلك.
نشرتها:
إيفا كازيميروفا ، باحثة في مختبر البيانات العصبية ، اختصاصي معالجة الكلام.
Offtop : هل تحب المقالة؟ في الواقع ، لدينا مجموعة من هذه المهام المثيرة للاهتمام في ML ، والرياضيات والبرمجة ، ونحن بحاجة إلى العقول. هل أنت فضولي؟ تعال إلينا! البريد الإلكتروني: hr@neurodatalab.com
المراجع- Rusz ، J. ، Cmejla ، R. ، Ruzickova ، H. ، Ruzicka ، E. القياسات الصوتية الكمية لتوصيف اضطرابات الكلام والصوت في مرض باركنسون المبكر غير المعالج. مجلة الجمعية الصوتية الأمريكية ، المجلد. 129 ، العدد 1 (2011) ، ص. 350-367. الوصول
- Farrús ، M. ، Hernando ، J. ، Ejarque ، P. Jitter and Shimmer قياسات للتعرف على المتحدث. وقائع المؤتمر السنوي للرابطة الدولية للاتصالات الكلام ، INTERSPEECH ، المجلد. 2 (2007) ، ص. 1153-1156. الوصول
- Zahorian ، S. ، Hu ، HA. الطريقة الطيفية / الزمنية لتتبع التردد الأساسي القوي. مجلة الجمعية الصوتية الأمريكية ، المجلد. 123 ، العدد 6 (2008) ، ص. 4559-4571. الوصول
- De Cheveigné، A.، Kawahara، H. YIN ، مقدر التردد الأساسي للكلام والموسيقى. مجلة الجمعية الصوتية الأمريكية ، المجلد. 111 ، العدد 4 (2002) ، ص. 1917-1930. الوصول