👩🏼‍🚒 🛀🏻 🤗 مثال لحساب تفاعل الإشارة باستخدام تحويل فورييه في MATLAB 🐓 🏬 🐨

عند حل مشاكل نقل البيانات من خلال خطوط ممثلة بخصائص التردد ، يتم تطبيق تحويلات فورييه - نقل الإشارات من المجال الزمني إلى مجال التردد والعكس بالعكس. بيئة MATLAB لديها مجموعة كاملة من الوظائف لحل مثل هذه المشاكل. في هذا العمل ، يتم تحليل مثال لحساب MATLAB رد فعل إشارة مرسلة عبر خط يتم قياس خصائصه عند الترددات التي لا تتزامن مع تردد نقل البيانات. آمل أن يسهّل هذا المثال فهم ميزات تقنية تحويل الإشارة في بيئة MATLAB.

شرط المهمة

من الضروري تحديد التغيير في شكل الإشارة الرقمية الثنائية التي تمر عبر المرشح وخط الإشارة. يتم ضبط الإشارة من خلال السعة ومعدل الإرسال. يتم تعيين عامل التصفية من الدرجة الثانية ، المقيس لتردد نقل البيانات ، من خلال الثوابت الزمنية. تتمثل وظيفة النقل لخط الإشارة باستجابة التردد المقيسة في شكل معقد.

البيئة المستخدمة لحساب البيانات وعرضها هي MATLAB R2015a.
تم أخذ العلاقات التالية المنشورة على موقع الويب www.StatEye.org لإصدار طريقة StatEye 3.0 GUI [1 ، 2 ، 3] كمثال للبيانات الأولية.

معدل البيانات في الثانية = 10.3125 جيجابت / ثانية. الثوابت الزمنية لمرشح الدرجة الثانية المعيارية هي نفسها ؛ وتبادلتهم ¾ من تردد إرسال البيانات. يتم تمثيل خط الإشارة باستجابة التردد. تم قياس الخاصية عند القناة. f = 0.006495: 0.0012475: 20 جيجا هرتز. العدد المحدد لنقاط أخذ العينات لتحويل فورييه: النقاط = 2 ^ 13.

يوضح الشكل 1 نتائج نقل البيانات وتسلسلها ومعالجة البيانات التي تمت مناقشتها في هذه الورقة. يتم تنفيذ الانتقال من المجال الزمني إلى نطاق التردد والعكس بالعكس باستخدام خوارزمية تحويل فورييه السريع (FFT).
الصورة

الشكل 1. قناة البيانات. إشارة الإدخال iSignal.Tx ، إشارة خرج المرشح iSignal.Filter_out ، خط إشارة الإخراج iSignal.Rx. الخصائص الموضحة في الرسم التخطيطي تناقش أدناه.

تسلسل الحساب

في هذا العمل ، يتم إجراء الحسابات الرئيسية في مجال التردد. لهذا ، يتم نقل الإشارة الأصلية من المجال الزمني إلى مجال التردد باستخدام تحويل فورييه ، وضرب الخصائص الطيفية للإشارة والمرشح وخط الإشارة ، تم العثور على إشارة خرج المسار ، والتي يتم نقلها من مجال التردد إلى المجال الزمني بواسطة تحويل فورييه العكسي.

معدل نقل البيانات أعلى مرتين من التردد الذي يتم فيه إرسال البيانات. أقصى تردد لخط الإشارة المقيس الأقصى (channel.f) = 20 جيجا هرتز. عند هذا التردد ، يمكن إرسال البيانات بسرعة 40 جيجابت / ثانية (كحد أقصى 2 * (channel.f)).

الحد الأقصى لمعدل نقل البيانات ، الذي لا يتجاوز الحد الأقصى لمعدل الإرسال على خط الإشارة 40 جيجابت / ثانية ومعدل الإرسال المتعدد bps = 10.3125 جيجابت / ثانية ، هو fmax = 30.9375 جيجابت / ثانية ، التعددية N = 3 (N = fmax / bps). علاوة على ذلك ، يتم استخدام fmax كتردد محدد لحساب استجابة الإشارة باستخدام تحويل Fourier.

ترجمة إشارة الإدخال إلى مجال التردد

تقدير الوقت لبناء إشارة الإدخال (بت البيانات) في المجال الزمني Ts = 1 / fmax ؛ Ts = 3.232e-11 ثانية. بعد تطبيعه فيما يتعلق بمدة الإشارة ، يتكون الخط الزمني من 2 ^ 13 نقطة (نقاط) ، يشمل المقياس المصفوفة التالية من نقاط الوقت = bps / Ts. * (1: نقاط). وتتكون الإشارة المنفصلة المنفصلة بمعدل إرسال قدره bps = 10.3125 جيجابت / ثانية ، وتتكون التكمية مع فترة Ts = 1 / fmax من ثلاث نقاط في المدى من 10 إلى 11 وحدة من الوقت المقيس. يمكن بناء إشارة اتساع الوحدة في أي مكان آخر على المخطط الزمني ، ولكن من الأفضل التراجع عن الحواف لرؤية الخلفية والحالة العابرة لإشارة الإخراج بشكل كامل. يظهر في الشكل 2 إشارة نبض (بت البيانات) تم إنشاؤها باستخدام أوامر MATLAB التالية.

iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0;

الشكل 2 الشكل 2. إشارة نبض الإدخال iSignal.Tx ، بت البيانات.

تتم ترجمة إشارة iSignal.Tx إلى مجال التردد بواسطة وظائف FFT التالية.

 iSignal.shiftedPSD = fft(iSignal.Tx); iSignal.PSD = fftshift(iSignal.shiftedPSD);

تقوم وظيفة تحويل فورييه fft ببناء طيف متناظر للإشارة في مناطق الترددات الموجبة والسالبة ، التي يكون أقصى تردد لها في وسط الطيف (انظر الشكل 3). تستعيد وظيفة fftshift الطيف بتحويل التردد الصفري للإشارة إلى المركز كما هو موضح في الشكل 4.

استبانة تردد الطيف fs = fmax / points ؛ تتراوح ترددات الطيف من -fmax / 2 إلى fmax / 2-fs وتساوي f = -fmax / 2: fs: fmax / 2-fs؛

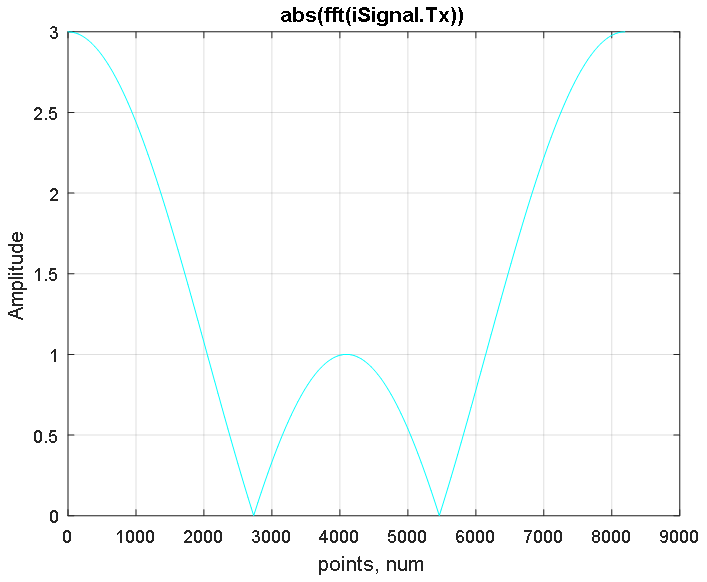الصورة

الشكل 3. استجابة السعة للطيف المتحول لإشارة iSignal.Tx التي تم الحصول عليها باستخدام FFT.

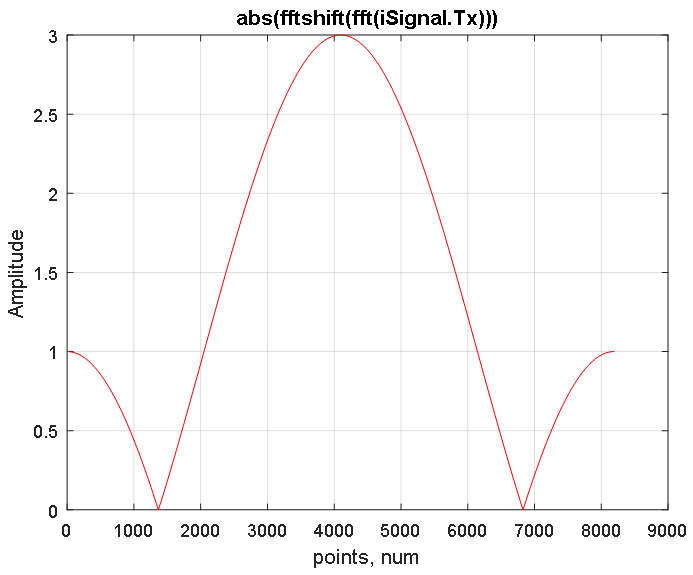الصورة

الشكل 4. استجابة السعة للطيف المعاد بناؤه لإشارة iSignal.Tx الموضحة في الشكل 3. 2 ^ 13 عينات. متوسط العد عند 4097 يقابل التردد الصفري. تقع الترددات السلبية على الجانب الأيسر (من 1 إلى 4096 نقطة) ، ومنطقة الترددات الإيجابية على الجانب الأيمن (من 4098 إلى 8192 نقطة).

وظيفة التحويل لمرشح التمرير المنخفض المقيس

في هذا المثال ، تحتوي دالة التحويل لمرشح الدرجة الثانية على النموذج

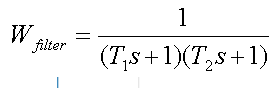
الصورة

حيث T1 و T2 عبارة عن ثوابت وقت التصفية. الترددات 1 / T1 متساوية وتم ضبط 1 / T2 بالنسبة للتردد الذي يتم إرسال البيانات عنده: 1 / T1 = 1 / T2 = 0.75 * بت في الثانية (bps = 10.3125 جيجابت / ثانية).

عرض النطاق الترددي للمرشح

 f_nrm =fmax/bps/points.*(-points/2:points/2-1).

عامل

 s = f_nrm .* j;

ويبين الشكل 6 خاصية طور الاتساع للمرشح المقيس للترددات الموجبة والسالبة المقيسة فيما يتعلق بتردد إرسال الإشارة. ويبين الشكل 6 خاصية تردد الاتساع اللوغاريتمي للمرشح.

الصورة

الرقم 5 الشكل 5. سمة مرحلة السعة لمرشح تطبيع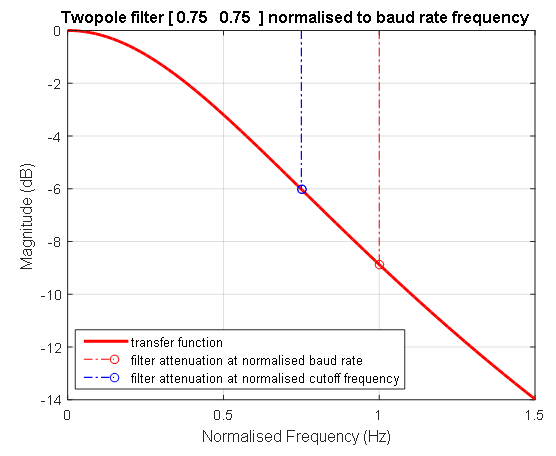

الصورة

الشكل 6 الشكل 6. استجابة تردد طور السعة اللوغاريتمية لمرشح مقيّس. يوضح الخط المتقطع الأزرق موضع تردد المرشح بقيمة 0.75 من التردد الذي يتم إرسال البيانات عنده. عند هذا التردد (1 / T1 = 1 / T2) ، يكون معامل إرسال مرشح الدرجة الثانية -6 ديسيبل. يشير الخط الأحمر المتقطع إلى تردد الوحدة التي يتم عندها إرسال البيانات.

ترجمة نتائج قياس خط الإشارة إلى نوع دالة التحويل

تتضمن خصائص مرحلة السعة المقاسة لخط الإشارة 1599 عينة في النطاق حتى GHz 20 بخطوة ثابتة تبلغ 12.475 ميجاهرتز. ويحتوي على قيم التردد التالية: channel.f = 0.006495: 0.0012475: 20 جيجا هرتز. في البداية ، تم تمثيل خط الإشارة بواسطة خاصية أربعة أطراف. تم تحويل هذه الخاصية واستخدامها في المثال كدالة معقدة ذات بعد واحد.

لا تتزامن الترددات المميزة لخط الإشارة التي تم الحصول عليها نتيجة القياس مع ترددات طيف إشارة الإدخال التي هي مضاعفات تردد إرسال البيانات. بالإضافة إلى ذلك ، يحتوي طيف خط الإشارة على ترددات موجبة فقط ولا يحتوي على ترددات في منطقة الصفر. يحتوي طيف إشارة الدخل على ترددات موجبة وصفرية وسالبة.
لتحويل خصائص خط الإشارة إلى دالة تحويل - خاصية تتزامن تردداتها مع ترددات طيف إشارة الإدخال ، يتم اتخاذ الخطوات التالية.

1. حساب اتساع خصائص الخط بتردد صفري باستنتاجه. لهذا ، من عشر نقاط من خاصية السعة الأقرب إلى التردد الصفري ، تم العثور على معاملات كثيرات الحدود الخطية التي تقارب خاصية السعة:

 [a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);

المعامل متعدد الحدود الثاني الموجود يساوي اتساع الخاصية عند التردد الصفري:

 channel.dc = a(2);

2. تؤخذ استجابة الطور عند تردد صفر مساوية للصفر.

 channel.dcPhase = 0.00;

3. يتم إعادة حساب خصائص السعة channel.abs وطور channel.phase لخط الإشارة بقيم بتردد صفري على تردد طيف إشارة الإدخال (f = -fmax / 2: fmax / points: fmax / 2-fmax / points) مع استقراء الخصائص إلى منطقة الترددات السالبة والصفر:

 ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);

دالة التحويل التي تم الحصول عليها - ترد استجابة تردد طور السعة للقناة في منطقة التردد المنخفض في الشكل 7. وتظهر خصائص تردد الاتساع لخط الإشارة المقيس ووظيفة التحويل المحسوبة في نطاقات التردد الكاملة في الشكل 8. وتظهر الخصائص نفسها في مساحة الطور في الشكل 9.

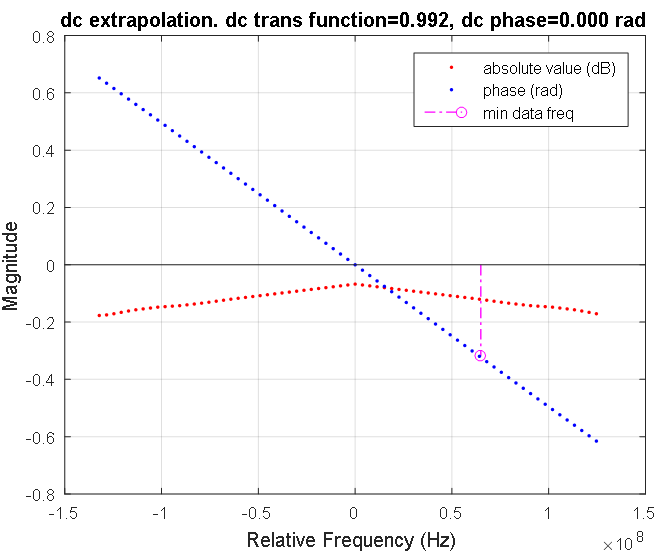الصورة

الشكل 7. وظيفة نقل خط الإشارة في منطقة التردد المنخفض. تشير النقاط الحمراء والزرقاء إلى السعة المنفصلة وخصائص الطور ، على التوالي. يتم عرض استجابة السعة بالديسيبل ، المرحلة بالراديان. يشير الخط الوردي إلى أدنى تردد للخاصية المقاسة لخط الإشارة. معامل الإرسال عند تردد صفر هو 0.992.

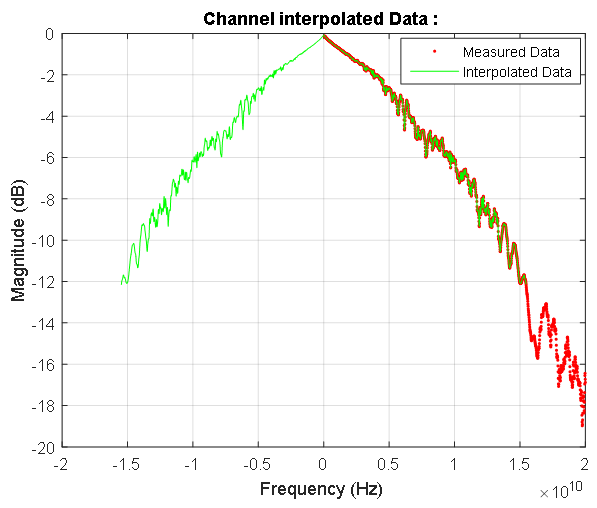الصورة

الشكل 8. استجابة التردد لخط الإشارة. تشير النقاط الزرقاء إلى البيانات المعقدة للخط المقاس. يتم تمييز الاعتماد المتماثل المحسوب لكسب خط الإشارة عند ترددات طيف إشارة الإدخال باللون الأحمر. في منطقة التردد الصفري ، تظهر هذه الخاصية في الشكل 7.

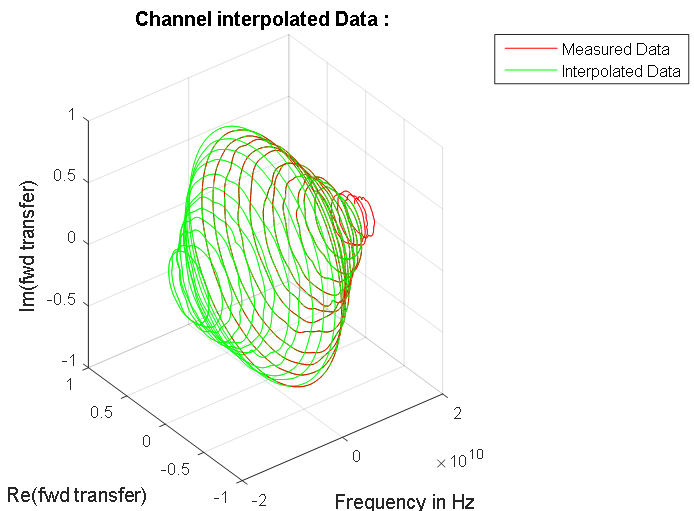الصورة

الشكل 9. خصائص تردد طور السعة لخط البيانات المقيس وطيفه المقيس.

حساب استجابة الإشارة

يتم الحصول على الاستجابة (الاستجابة لتأثير الإدخال) في مجال التردد عن طريق ضرب طيف الإشارة في منتج وظائف نقل العناصر التي تربط التفاعل بإشارة الإدخال. في حالتنا ، تمر الإشارة عبر المرشح وخط الإشارة.
يتم استخدام ifft تحويل معكوس فورييه لنقل الإشارة من مجال التردد إلى المجال الزمني.

يتم احتساب إخراج المرشح في مجال الوقت iSignal.Filter_out على أنه

 TransFunction.PSD = iSignal.PSD .* Filter.PSD_Tx; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));

تساوي إشارة خرج خط iSignal.Rx منتج طيف إشارة الإدخال ووظائف النقل للمرشح وخط الإشارة مع النقل اللاحق للإشارة المستقبلة من مجال التردد إلى المجال الزمني.

 TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD));

ويبين الشكل 10 استجابة المرشح لنبض الإدخال المثالي واستجابة القناة.

الصورة

الشكل 10. مرشح الإخراج (الرسم البياني الأحمر) وإخراج خط البيانات (الرسم البياني الأخضر). إشارة إدخال المرشح - يظهر نبض واحد في الشكل 2. إدخال خط الإشارة هو إشارة خرج المرشح.

التطبيق. تستخدم رمز m MATLAB

قائمة

 clear all %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Ini data %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% bps = 1.03125e+10; FilterParam = [0.75 0.75]; points = 2^13; load('channel'); N = floor(max(channel.f)*2/bps); fmax = N*bps; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Signal %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % normalise all the scales for the bit rate time = bps/fmax .* (1:points); iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0; figure plot(time(1:t1+10), iSignal.Tx(1:t1+10),'b'); hold on plot(time(1:t1+10), iSignal.Tx(1:t1+10),'xb'); grid on xlabel('Normalised Time, tick Ts = 1/fmax'); ylabel('Normalised Amplitude'); title(['Pulse, data bit']); iSignal.shiftedPSD = fft(iSignal.Tx); figure plot(abs(iSignal.shiftedPSD),'c'); grid on xlabel('points, num'); ylabel('Amplitude'); title(['abs(fft(iSignal.Tx))']); iSignal.PSD = fftshift(iSignal.shiftedPSD); figure plot(abs(iSignal.PSD),'r'); grid on xlabel('points, num'); ylabel('Amplitude'); title(['abs(fftshift(fft(iSignal.Tx)))']); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Filter %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% f_nrm =fmax/bps/points.*(-points/2:points/2-1); s = f_nrm .* j; Filter_PSD = 1 ./(1 + s/FilterParam(1)) ./ (1 + s/FilterParam(2)); figure [AX,H1,H2] = plotyy (f_nrm, abs(Filter_PSD), f_nrm, phase(Filter_PSD)); hold(AX(1)); hold(AX(2)); set(H1,'LineWidth',2); grid(AX(2),'on'); xlabel('Normalised Frequency (Hz)'); set(get(AX(1),'Ylabel'),'String','Gain'); set(get(AX(2),'Ylabel'),'String','Phase, rad'); title(['Twopole filter [' sprintf(' %3.2f ', FilterParam) '] normalised to baud rate frequency']); figure plot_handles_Filter = plot(f_nrm(points/2 + 1:points), 20*log10(abs(Filter_PSD(points/2 + 1:points))), 'r', 'linewidth', 2); hold on stem_handles_br = stem(1, 20*log10(abs(Filter_PSD(max(find(f_nrm < 1))))), '-.ro'); hold on stem_handles_c = stem(FilterParam, [20*log10(abs(Filter_PSD(max(find(f_nrm < FilterParam(1)))))) 20*log10(abs(Filter_PSD(max(find(f_nrm < FilterParam(2))))))], '-.bo'); grid legend_handles = [plot_handles_Filter, stem_handles_br(1), stem_handles_c(1)]; legend(legend_handles, 'transfer function', 'filter attenuation at normalised baud rate', 'filter attenuation at normalised cutoff frequency', 3); xlabel('Normalised Frequency (Hz)'); ylabel('Magnitude (dB)'); title(['Twopole filter [' sprintf(' %3.2f ', FilterParam) '] normalised to baud rate frequency']); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Channel %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % create negative frequencies, convert data to complex value, taking care about negative frequency channel.abs = abs(channel.s); channel.phase = angle(channel.s); %channel.s = channel.abs .* exp(+j.*channel.phase); [a] = polyfit(channel.f(1:10), channel.abs(1:10), 1); channel.dc = a(2); channel.dcPhase = 0.00; fs = fmax/points; % frequency step f = -fmax/2:fs:fmax/2-fs; % frequency matrix % create new data structure with linearly interpolated data ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); % correct for negative frequencies ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f); figure disp_points = 2*round(channel.f(1)/fs); stem_handles_br = stem(channel.f(1), angle(ichannel.tf(max(find(f < channel.f(1))))), '-.mo'); hold on plot_abs = plot(f(points/2-disp_points:points/2+disp_points), 20*log10(abs(ichannel.tf(points/2-disp_points:points/2+disp_points))), '.r', 'linewidth', 3); hold on plot_phase = plot(f(points/2-disp_points:points/2+disp_points), angle(ichannel.tf(points/2-disp_points:points/2+disp_points)), '.b', 'linewidth', 3); grid legend_handles = [plot_abs, plot_phase, stem_handles_br(1)]; legend(legend_handles, 'absolute value (dB)', 'phase (rad)', 'min data freq', 3); xlabel('Relative Frequency (Hz)'); ylabel('Magnitude'); title(sprintf('dc extrapolation. dc trans function=%4.3f, dc phase=%4.3f rad', abs(ichannel.tf(points/2+1)), angle(ichannel.tf(points/2+1)))); figure plot(channel.f, 20*log10(channel.abs), '.r', 'linewidth', 3); hold on plot(f, 20*log10(ichannel.abs), 'g'); grid on legend('Measured Data', 'Interpolated Data', 3); xlabel('Frequency (Hz)'); ylabel('Magnitude (dB)'); title(['Chnnel interpolated Data : ']); figure plot3(channel.f, real(channel.s), imag(channel.s),'r'); hold on plot3(f, real(ichannel.tf), imag(ichannel.tf),'g'); grid on legend('Measured Data', 'Interpolated Data'); xlabel('Frequency in Hz'); ylabel('Re(fwd transfer)'); zlabel('Im(fwd transfer)'); title(['Chnnel interpolated Data : ']); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Response %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % filter Output TransFunction.PSD = iSignal.PSD .* Filter_PSD; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD)); % pass through channel TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD)); figure plot(time, iSignal.Filter_out,'r'); hold on [max_Tx, time_maxTx] = max(iSignal.Filter_out); [min_Tx, time_minTx] = min(iSignal.Filter_out); [max_Rx, time_maxRx] = max(iSignal.Rx); dtime_p5= round((time_maxRx - time_maxTx)*time(1) -1); plot(time - dtime_p5, iSignal.Rx,'g'); hold on plot(time, iSignal.Filter_out,'rx'); axis([(time_maxTx*time(1) - 3) (time_maxTx*time(1) + 5) (min_Tx-0.15) (max_Tx+0.1)]) grid on legend('Filter out','Rx', 2); xlabel('Normalised Time'); ylabel('Normalised Amplitude'); title(sprintf('Transmit pulse (Tx) max= %4.3f; Response (Rx) max (h0)= %4.3f', max(iSignal.Filter_out), max(iSignal.Rx)));

قائمة ببليوغرافية

1. IEEE802.3ap. نتائج محاكاة NRZ بسرعة 10.3125 جيجابت في الثانية باستخدام "StatEye" و "إشارة إلى نموذج التداخل" على مكونات القناة المتتالية. شانون سوير وتشارلز مور / اجيلنت تكنولوجيز. 24 يناير 2005 www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf

2. ما هي StatEye. IEEE 803.3ap Task Force. 16 سبتمبر 2004 www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf

3. اتفاقية Stat Eye / IBM. ستيف أندرسون. Xilinx، Inc. www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf

مثال لحساب تفاعل الإشارة باستخدام تحويل فورييه في MATLAB