التدريب GAN الاستدامة

تم نشر فكرة GAN لأول مرة بواسطة Jan Goodfellow Generative Adversarial Nets، Goodfellow et al 2014 ، وبعد ذلك أصبحت GANs واحدة من أفضل النماذج التوليدية.

كما هو الحال مع أي نموذج تولد آخر ، فإن مهمة GAN هي إنشاء نموذج بيانات ، وبشكل أكثر تحديدًا ، معرفة كيفية إنشاء عينات من توزيع في أقرب وقت ممكن لتوزيع البيانات (عادة ما تكون هناك مجموعة بيانات محدودة الحجم نريد أن نمثل فيها توزيع البيانات).

تتمتع GANs بعدد كبير من المزايا ، ولكن لها عيب واحد كبير - فهي صعبة التدريب.

في الآونة الأخيرة ، تم إصدار عدد من الأعمال حول استدامة GAN:

• تحسين GAN لأصل التدرج مستقر محليًا ، Vaishnavh Nagarajan ، J. Zico Kolter ، 2017
• الأعداد الرقمية لـ GANs ، Lars Mescheder et al ، 2017

مستوحاة من أفكارهم ، قمت ببعض البحث.

حاولت أن أجعل النص بسيطًا قدر الإمكان ، وإذا أمكن ، استخدم أبسط الرياضيات فقط. لسوء الحظ ، من أجل تبرير لماذا يمكننا النظر في خصائص حقول المتجه ثنائية الأبعاد ، علينا أن نحفر قليلاً في اتجاه حساب التباينات. ولكن إذا كان شخص ما ليس على دراية بهذه المصطلحات ، فيمكنك المتابعة بأمان على الفور للنظر في حقول المتجهات ثنائية الأبعاد لأنواع مختلفة من GAN.

سنحاول الآن النظر تحت غطاء إجراء التدريب وفهم ما يحدث هناك.

GAN ، المشكلة الرئيسية

تتكون GANs من شبكتين عصبيتين: تمييز ومولد. مولد - يسمح لك بأخذ عينات من بعض التوزيع (عادة ما يسمى توزيع المولد). يتلقى المتميز عينات إدخال من مجموعة البيانات الأصلية والمولد ويتعلم توقع مصدر هذه العينة (مجموعة البيانات أو المولد).

مخطط GAN:



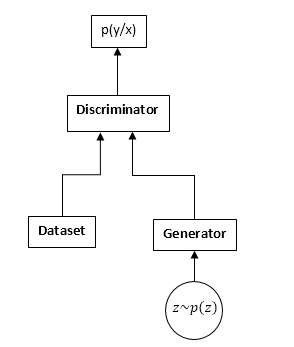
عملية التدريب GAN على النحو التالي:

1. نأخذ عينات n من مجموعة البيانات وعينات من المولد.
2. نقوم بإصلاح أوزان المولد وتحديث معلمات التمييز. هذه مهمة تصنيف شائعة. نحن فقط لا نحتاج إلى تدريب المميِّز حتى التقارب. وكثيرا ما يتدخل أيضا.
3. نقوم بإصلاح أوزان التمايز ونقوم بتحديث أوزان المولد ، حتى يبدأ التمايز في التفكير في أن عيناتنا من مجموعة البيانات وليس من المولد.
4. نكرر 1-3 ، حتى يأتي المتميز والمولد في حالة توازن (أي أنه لا يمكن لأي من الآخرين "خداع" الآخر).

لن نفحص بالتفصيل عملية التعلم GAN. هناك العديد من المقالات التي تشرح هذه العملية بالتفصيل على الإنترنت ، وعلى المحور بشكل خاص.

سنكون مهتمين بشيء مختلف تمامًا. على وجه التحديد ، نظرًا لأننا نتنافس مع شبكتين عصبيتين ، تتوقف المهمة عن البحث عن الحد الأدنى (الحد الأقصى) ، ولكنها تتحول في حالات معينة إلى بحث عن نقطة السرج (أي ، في الخطوتين 2 و 3 ، نحاول نفس الوظيفة تكبير بواسطة معلمات التمييز وتقليلها بواسطة معلمات المولد) ، وفي الخطوتين الأكثر عمومية 2 و 3 يمكننا تحسين الوظائف المختلفة تمامًا. من الواضح أن مشكلة الحد الأدنى هي حالة خاصة لتحسين الوظائف المختلفة - يتم أخذ وظيفة واحدة بعلامات مختلفة.

دعونا نلقي نظرة على هذا في الصيغ. نفترض أن pd (x) هو التوزيع الذي يتم من خلاله أخذ عينات مجموعة البيانات ، ص (x) هو توزيع المولد ، D (x) هو الناتج من التمييز.

عند تدريب أحد المتميزين ، غالبًا ما نزيد من هذه الوظائف:

$$

ناقلات التدرجات:

$$

$$v = \ \ nabla_ \ theta J \ = \ int {\ frac {p_d (x)} {D (x)} \ nabla_ \ theta D (x) \ dx \ + \ \ int {\ frac {p_g (x )} {1 \ - \ D (x)} \ nabla_ \ theta D (x) dx}}$$

عند تدريب المولد ، نقوم بزيادة:

$$

$$I \ = \ - \ int {p_g (x) سجل (1 \ - \ D (x)) dx}$$

ناقل التدرجات في هذه الحالة:

$$

$$u \ = \ \ nabla_ \ varphi I \ = \ - \ int {{\ nabla_ \ varphi p} _g (x) سجل (1 \ - \ D (x)) dx}$$

في المستقبل ، سنرى أنه يمكن استبدال الوظائف على التوالي بما يلي:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

أين $$$f_1 ، f_2 ، f_3$ يتم تحديدها وفقًا لقواعد معينة. بالمناسبة ، يستخدم إيان غودفيلو في مقالته الأصلية $$$f_1 و f_2$ كما هو الحال عند تدريب تمييز منتظم ، و $$$f_3$ يختار ذلك لتحسين التدرجات في المرحلة الأولية من التدريب:

$$

$$f_1 \ left (x \ right) = تسجيل \ اليسار (x \ right) ، \ f_2 \ left (x \ right) = تسجيل \ اليسار (1 \ - \ x \ right) ، f_3 \ left (x \ right) = تسجيل \ اليسار (x \ right)$$

للوهلة الأولى ، تبدو المهمة مشابهة جدًا للمهمة المعتادة للتعلم مع نزول التدرج (الصعود). لماذا ، إذن ، اتفق كل من جاء عبر تدريب GAN على أنه كان صعبًا للغاية؟

الجواب يكمن في بنية حقل المتجه ، الذي نستخدمه لتحديث معلمات الشبكات العصبية. في حالة مشكلة التصنيف المعتادة ، نستخدم فقط متجه التدرج ، أي أن المجال محتمل (الوظيفة المحسنة نفسها هي إمكانات هذا المجال المتجه). ولحقول المتجهات المحتملة بعض الخصائص الرائعة ، أحدها هو عدم وجود منحنيات مغلقة. أي أنه من المستحيل السير في دوائر في هذا المجال. ولكن عند تدريب GAN ، على الرغم من حقيقة أن حقول المتجه للمولد والمميز محتملة بشكل منفصل (نفس التدرج) ، فلن يكون مجال المتجه الإجمالي محتملًا. وهذا يعني أنه في هذا المجال يمكن أن تكون هناك منحنيات مغلقة ، أي يمكننا المشي في دوائر. وهذا أمر سيئ للغاية.

السؤال الذي يطرح نفسه: لماذا ، على الرغم من كل ذلك ، نجحنا في تدريب GAN بنجاح كبير ، ربما لا يزال المجال غير منطقي (محتمل)؟ وإذا كان الأمر كذلك ، فلماذا هو معقد للغاية؟
سوف أسير قدما ، للأسف ، الحقل غير محتمل ، ولكن به عدد من الخصائص الجيدة. لسوء الحظ ، فإن المجال حساس جدًا أيضًا لتحديد معلمات الشبكات العصبية (اختيار وظائف التنشيط واستخدام DropOut و BatchNormalization وما إلى ذلك). لكن أول الأشياء أولاً.

حقل GAN "التدرج"

سننظر في وظائف التعلم GAN في الشكل الأكثر عمومية:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

نحن بحاجة إلى تحسين كلتا الوظيفتين في نفس الوقت. بافتراض أن D (x) و pg (x) هي وظائف مرنة تمامًا ، أي يمكننا أخذ أي رقم في أي وقت ، بغض النظر عن النقاط الأخرى. هذه حقيقة معروفة جيدًا من حساب الاختلافات - تحتاج إلى تغيير الوظيفة في اتجاه المشتق المتغير لهذه الوظيفة (بشكل عام ، تناظرية كاملة لارتفاع التدرج).

نكتب المشتقة المتنوعة:

$$

$$\ frac {\ جزئي J} {\ جزئي D (x)} = p_d (x) f_1 '(D (x)) \ + \ p_g (x) f_2' (D (x))$$

$$

$$\ frac {\ جزئي I} {\ جزئي p_g (x)} = f_3 (D (x))$$

سننظر فقط في الوظيفة الأولى (بالنسبة للتمييز) ، وللثاني سيكون كل شيء هو نفسه.

ولكن بالنظر إلى أنه في الواقع لا يمكننا تغيير الوظيفة إلا في مجموعة الوظائف التي يمكن أن تمثلها شبكتنا العصبية ، سنكتب:

$$$$ display $$ ∆D (x) = \ frac {\ جزئي D (x)} {\ جزئي θ_j} Δθ_j $$ display $$

التغييرات في معلمات الشبكة ، بشكل عام ، نزول التدرج المعتاد (الارتفاع):

$$$$ display $$ ∆θj = \ frac {\ جزئي J} {\ جزئي θ_j} μ $$ display $$

µ هو معدل التعلم. حسنًا ، المشتق فيما يتعلق بمعلمات الشبكة:

$$

$$\ frac {\ جزئي J} {\ جزئي \ theta_j} = \ int {\ frac {\ جزئي J} {\ جزئي D (y)} \ frac {\ جزئي D (y)} {\ جزئي \ theta_j} dy }$$

والآن نضع كل ذلك معًا:

$$

$$∆D (x) = \ sum_ {j} {\ frac {\ جزئي D (x)} {\ جزئي \ theta_j} \ int {\ frac {\ جزئي J} {\ جزئي D (y)} \ frac { \ D جزئي (y)} {\ جزئي \ theta_j} dy} \ mu \ = \ mu \ int \ frac {\ جزئي J} {\ جزئي D (y)}} \ sum_ {j} {\ frac {\ جزئي D (x)} {\ جزئي \ theta_j} \ frac {\ جزئي د (خ)} {\ جزئي \ theta_j} dy \ = \} \ mu \ int {\ frac {\ جزئي J} {\ جزئي D (y )} K_ \ theta (x، y) dy}$$

أين: $$$K_ \ theta (x، y) \ = \ sum_ {j} {\ frac {\ جزئي D (x)} {\ جزئي \ theta_j} \ frac {\ جزئي D (x)} {\ جزئي \ theta_j} \ }$

لم يسبق لي أن رأيت هذه الميزة في الأدبيات المتعلقة بتعلم الآلة ، لذلك سأطلق عليها النواة البارامترية للنظام.

حسنًا ، أو إذا انتقلنا إلى خطوات مستمرة في الوقت المناسب (من معادلات الفروق إلى المعادلات التفاضلية) ، نحصل على:

$$

$$\ frac {d} {dt} D (x) \ = \ \ int {\ frac {\ جزئي J} {\ جزئي D (y)} K_ \ theta (x، y) dy}$$

تظهر هذه المعادلة العلاقة الداخلية للحقل الأصلي (نقطة التمييز بالنسبة للمميز) وتقييس الشبكة العصبية. نحصل على معادلة مماثلة تمامًا للمولد.

بالنظر إلى أن K (x، y) (النواة المعلمية) هي وظيفة محددة موجبة (حسنًا ، كيف يمكن تمثيلها كمنتج عددي للتدرجات في النقاط المقابلة) ، يمكننا أن نستنتج أن أي تغييرات في الوظائف المدربة (تمييز ومولد) تنتمي إلى مساحة هيلبرت التي تم إنشاؤها بواسطة النواة ، أي ك (س ، ص). أتساءل عما إذا كان من الممكن الحصول على أي نتائج ذات معنى هنا. لكننا لن ننظر في هذا الاتجاه بعد ، ولكننا سننظر في الاتجاه الآخر.

كما ترون ، يتم تحديد استقرار GAN من خلال مكونين: المشتقات المتنوعة للوظائف وتحديد معلمات الشبكة العصبية. مهمتنا هي أن نرى كيف يتصرف هذا المجال بشكل نقطي ، أي إذا كانت شبكتنا يمكن أن تمثل أي وظيفة على الإطلاق. تتحول المهمة إلى تحليل لمجال متجه ثنائي الأبعاد. وهذا ، في اعتقادي ، في قوتنا.

الاستدامة

لذا ، فإننا نعتبر حقل المتجه التالي:

$$

$$\ frac {d} {dt} D (x) = \ \ frac {\ جزئي J} {\ جزئي D (x)}$$

$$

$$\ frac {d} {dt} p_g (x) = \ \ frac {\ جزئي I} {\ جزئي p_g (x)}$$

من الواضح أن هذه المعادلات يمكن اعتبارها لنقطة واحدة فقط x ، مع مراعاة كيف تبدو مشتقاتنا المتغيرة:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D)$$

الشرط الأول لنظام المعادلات هذا هو أن الأطراف اليمنى يجب أن تصل إلى 0 عندما:
$$$p_d = p_g$

خلاف ذلك ، سنحاول تدريب النموذج ، والذي من الواضح أنه لن يتقارب مع الحل الصحيح. على سبيل المثال د يجب أن يكون حلاً للمعادلة التالية:

$$

$$f_1 ^ \ prime (D) \ + \ f_2 ^ \ prime (D) \ = \ 0$$

نشير إلى هذا الحل على أنه $$$D0$ .

بالنظر إلى حقيقة أن pg (x) هي كثافة الاحتمال إلى الجانب الأيمن ، يمكننا إضافة أي رقم دون انتهاك المشتقات. من أجل توفير 0 من الجانب الأيمن عند النقطة المطلوبة ، اطرح القيمة في t. $$$D0$ (يجب أن يتم ذلك إذا أردنا أن ننظر في pg نقطة - الانتقال من حقل معلمات بكثافات الاحتمالية إلى الحقول الحرة).

ونتيجة لذلك ، نحصل على الحقل التالي:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D) \ - \ f (D0)$$

من الآن فصاعدا ، سوف ندرس النقاط الساكنة واستقرار الحقول من هذا النوع.
يمكننا دراسة نوعين من الاستقرار: محلي (على مقربة من نقطة السكون) وعالمي (باستخدام طريقة دالة ليابونوف).

لدراسة الاستقرار المحلي ، من الضروري حساب مصفوفة Jacobi للحقل.
لكي يكون الحقل "مستقرًا" محليًا ، من الضروري أن يكون للقيم الذاتية جزء حقيقي سلبي.

أنواع مختلفة من GAN

1. GAN الكلاسيكي

   
   
   في GAN الكلاسيكي ، نستخدم logloss المنتظم:
   

   $$

   
   لتدريب المتميز ، من الضروري تعظيمه ؛ للمولد ، لتقليله. في هذه الحالة ، سيبدو الحقل كما يلي:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ -log (1-D) \ + \ log (\ frac {1} {2})$$
   
   دعنا نرى كيف ستتطور المعلمات (pg و D) في هذا المجال. للقيام بذلك ، استخدم نص بايثون البسيط هذا:
   
   
   البرنامج النصي

   def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = -np.log(1.-d) + np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   لنقطة البداية $$$p_g = 0.9، D = 0.25$ سيبدو هكذا:
   
   
   
   ستكون نقطة الاستراحة لمثل هذا الحقل: pg = pd و D = 0.5
   
   يمكن للمرء بسهولة التحقق من أن الأجزاء الحقيقية من القيم الذاتية لمصفوفة جاكوبي سلبية ، أي أن المجال مستقر محليًا.
   لن نتعامل مع دليل الاستدامة العالمية. ولكن إذا كان الأمر مثيرًا للاهتمام ، يمكنك اللعب باستخدام نص Python النصي والتأكد من أن الحقل مستقر لأي قيم أولية صالحة.

2. تعديل جان Goodfellow

   
   ناقشنا بالفعل أعلاه أن Ian Goodfellow في المقالة الأصلية استخدم نسخة معدلة قليلاً من GAN. بالنسبة لنسخته ، كانت الوظائف كما يلي:
   

   $$

   $$f_1 \ left (x \ right) = تسجيل \ اليسار (x \ right) ، \ f_2 \ left (x \ right) = تسجيل \ اليسار (1 \ - \ x \ right) ، f_3 \ left (x \ right) = تسجيل \ اليسار (x \ right)$$
   
   سيبدو الحقل كما يلي:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ log (D) \ - \ log (\ frac {1} {2})$$
   
   سيكون نص بايثون هو نفسه ، فقط تختلف الوظيفة الميدانية:
   
   
   البرنامج النصي

    def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = np.log(d) - np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   وبنفس البيانات الأولية ، تبدو الصورة كما يلي:
   
   
   
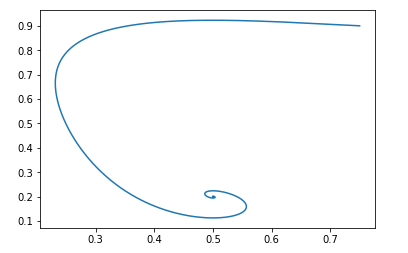
   ومرة أخرى ، من السهل التحقق من أن الحقل سيكون مستقرًا محليًا.
   هذا ، من وجهة نظر التقارب ، مثل هذا التعديل لا يضر بخصائص GAN ، ولكن له مزاياه الخاصة من حيث تدريب الشبكات العصبية.

3. واسرشتاين غان

   
   دعونا نلقي نظرة على وجهة نظر شعبية أخرى لـ GAN. تبدو الوظيفة المحسنة كما يلي:
   

   $$

   $$J \ = \ \ int {p_d (x) D (x) dx \ - \} \ int {p_g (x) D (x) dx}$$
   
   حيث ينتمي D إلى فئة وظائف 1-Lipschitz فيما يتعلق بـ x.
   نريد تكبيره بمقدار D وتقليله بواسطة pg.
   
   من الواضح في هذه الحالة: $$$f_1 \ left (x \ right) = x ، \ f_2 \ left (x \ right) = - x ، \ f_3 \ left (x \ right) = x$
   
   وسيبدو الحقل كما يلي:
   

   $$

   $$\ frac {d} {dt} D = \ p_d \ - {\ p} _g \ $$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ D$$
   
   في هذا المجال ، يمكن تخمين دائرة ذات مركز في نقطة ما بسهولة. $$$p_g = p_d، D = 0$ .
   أي ، إذا ذهبنا في هذا المجال ، فسوف نتجول دائمًا في دوائر.
   
   فيما يلي مثال لمسار في مثل هذا المجال:
   
   
   
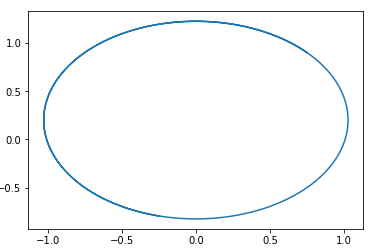
   السؤال هو ، لماذا اتضح بعد ذلك تدريب هذا النوع من GAN؟ الجواب بسيط للغاية - هذا التحليل لا يأخذ في الاعتبار حقيقة خاصية 1-Lipschitz لـ D. أي أننا لا نستطيع اتخاذ وظائف تعسفية. بالمناسبة ، هذا يتفق بشكل جيد مع نتائج مؤلفي المقالة ... لتجنب المشي في دائرة ، يوصون بتدريب المميّز على الالتقاء: Wasserstein GAN

4. خيارات GAN الجديدة

   
   اختيار الميزة $$$f_1 و f_2 و f_3$ يمكنك إنشاء خيارات GAN مختلفة. الشرط الرئيسي لهذه الوظائف هو ضمان وجود نقطة استراحة "صحيحة" واستقرار هذه النقطة (يفضل عالميًا ، ولكن على الأقل محليًا). أعطي القارئ الفرصة لاشتقاق القيود على الوظائف f1 و f2 و f3 اللازمة للاستقرار المحلي. الأمر سهل - ما عليك سوى التفكير في المعادلة التربيعية للقيم الذاتية لمصفوفة جاكوبي.
   
   سأعطي مثالاً لمثل GAN:
   

   $$

   $$f_1 (x) \ = \ -0.5x ^ 2 ، \ f_2 (x) \ = \ x ، \ f_3 (x) \ = \ -x$$
   
   مرة أخرى ، أقترح أن القارئ نفسه يبني مجال هذا GAN ويثبت استقراره. (بالمناسبة ، هذا واحد من المجالات القليلة التي يعتبر فيها دليل الاستقرار العالمي أمرًا أساسيًا - ما عليك سوى تحديد وظيفة Lyapunov ، والمسافة إلى نقطة الراحة). ضع في اعتبارك أن نقطة الراحة هي D = 1.

الخلاصة والمزيد من البحث

يمكن أن نرى من التحليل أعلاه أن جميع شبكات GAN الكلاسيكية (باستثناء Wassertein GAN ، التي لديها طرقها الخاصة لتحسين الاستقرار) لها حقول "جيدة". على سبيل المثال يتبع هذه الحقول نقطة راحة واحدة يكون فيها توزيع المولد مساوياً لتوزيع البيانات.

لماذا يعد تدريب GAN مهمة صعبة. الجواب بسيط - تحديد معايير الشبكات العصبية. باستخدام المعلمة "السيئة" ، يمكننا أيضًا الذهاب للتنزه في دوائر. على سبيل المثال ، تُظهر تجاربي أنه على سبيل المثال ، يؤدي استخدام BatchNormalization في أي شبكة إلى تحويل الحقل على الفور إلى حقل مغلق. وتنشيط Relu يعمل بشكل أفضل.

لسوء الحظ ، في الوقت الحالي لا توجد طريقة واحدة للتحقق نظريًا من عناصر الشبكة العصبية حول كيفية تغيير المجال. سوف يثبت لي من المحتمل أن تحقق في خصائص النواة المعلمية للنظام - $$$K_ \ theta (x، y)$ .

أردت أيضًا أن أتحدث عن طرق لتنظيم حقول GAN وإلقاء نظرة على ذلك من منظور الحقول ثنائية الأبعاد. النظر في خوارزميات التعلم التعزيز من هذا المنظور. وغير ذلك الكثير. ولكن للأسف ، تبين أن المقالة كبيرة جدًا على أي حال ، لذلك المزيد حول ذلك في وقت آخر.