مبدأ تشغيل الشبكة العصبية التلافيفية. فقط معقدة

لقد أدت الشبكات العصبية العميقة إلى اختراق في العديد من مهام التعرف على الصور ، مثل رؤية الكمبيوتر والتعرف على الصوت. الشبكة العصبية التلافيفية هي أحد الأنواع الشائعة للشبكات العصبية.

في الأساس ، يمكن اعتبار الشبكة العصبية التلافيفية شبكة عصبية تستخدم العديد من النسخ المتطابقة من نفس العصبون. هذا يسمح للشبكة أن يكون لديها عدد محدود من المعلمات عند حساب النماذج الكبيرة.


2D الشبكة العصبية التلافيفية

هذه التقنية مع عدة نسخ من نفس العصبون لها تشابه وثيق مع تجريد الوظائف في الرياضيات وعلوم الكمبيوتر. أثناء البرمجة ، تتم كتابة الوظيفة مرة واحدة ثم إعادة استخدامها ، دون أن تطلب منك كتابة نفس الرمز عدة مرات في أماكن مختلفة ، مما يسرع من تنفيذ البرنامج ويقلل من عدد الأخطاء. وبالمثل ، فإن الشبكة العصبية التلافيفية ، بمجرد تدريبها على الخلايا العصبية ، تستخدمها في العديد من الأماكن ، مما يسهل تدريب النموذج ويقلل الأخطاء.

هيكل الشبكات العصبية التلافيفية

لنفترض أنه تم إعطاء مهمة تتطلب التنبؤ من الصوت بما إذا كان هناك صوت شخص في الملف الصوتي.

عند الإدخال ، نحصل على عينات صوتية في نقاط زمنية مختلفة. يتم توزيع العينات بالتساوي.



أسهل طريقة لتصنيفها باستخدام شبكة عصبية هي توصيل جميع العينات بطبقة متصلة بالكامل. في هذه الحالة ، يتم توصيل كل إدخال بكل خلية عصبية.



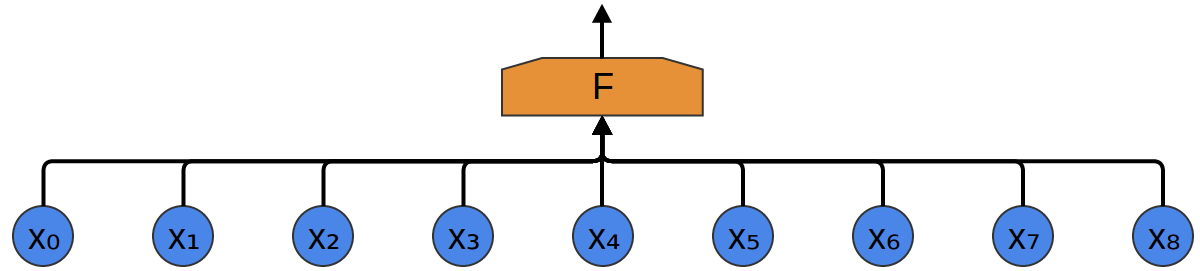
يأخذ نهج أكثر تعقيدًا في الاعتبار بعض التناظر في الخصائص الموجودة في البيانات. نولي الكثير من الاهتمام للخصائص المحلية للبيانات: ما هو تردد الصوت لفترة معينة؟ زيادة أم نقصان؟ وهكذا دواليك.

نحن نأخذ بعين الاعتبار نفس الخصائص في جميع الأوقات. من المفيد معرفة الترددات في البداية والوسط والنهاية. لاحظ أن هذه خصائص محلية ، لأنك تحتاج فقط إلى نافذة تسلسل صوتي صغيرة لتعريفها.

وبالتالي ، من الممكن إنشاء مجموعة من الخلايا العصبية A ، والتي تأخذ في الاعتبار أجزاء صغيرة من الوقت في بياناتنا. نظرة على جميع هذه القطاعات ، وحساب وظائف معينة. ثم ، يتم تغذية ناتج هذه الطبقة التلافيفية إلى طبقة متصلة بالكامل F.



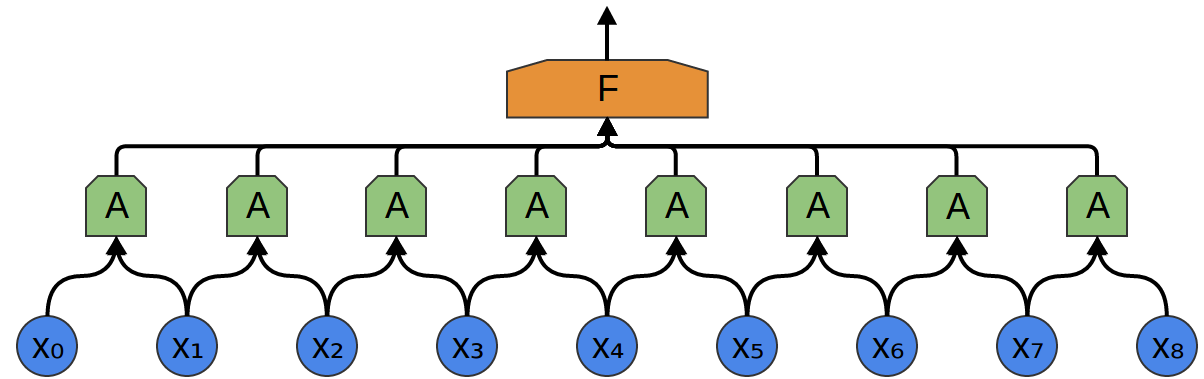
في المثال أعلاه ، قامت A بمعالجة مقاطع من نقطتين فقط. هذا نادر في الممارسة. عادة ، تكون نافذة طبقة الالتفاف أكبر بكثير.

في المثال التالي ، يتلقى A 3 أجزاء عند الإدخال. هذا أيضًا غير مرجح لمهام العالم الحقيقي ، ولكن ، لسوء الحظ ، من الصعب تصور A توصيل مدخلات متعددة.



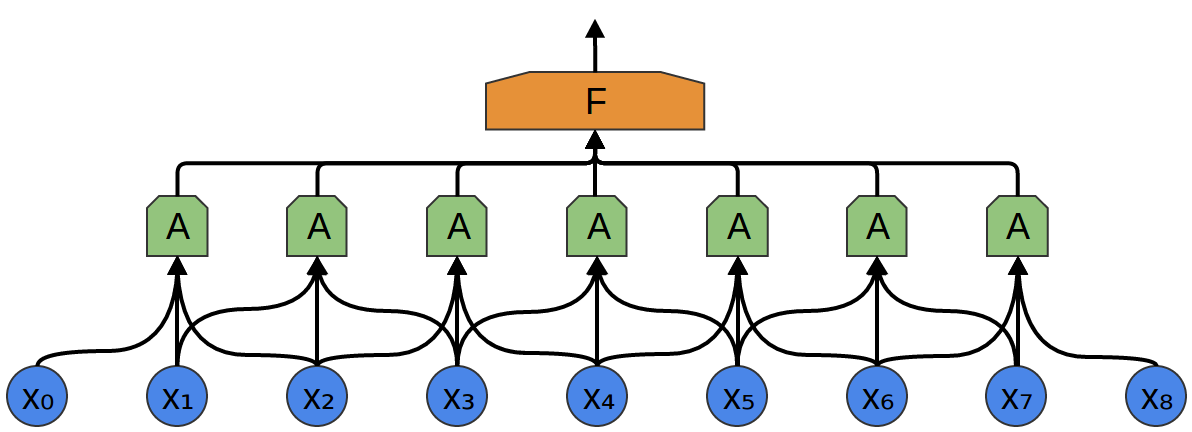
إحدى الخصائص اللطيفة للطبقات التلافيفية هي أنها مركبة. يمكنك تغذية ناتج طبقة تلافيفية إلى أخرى. تكتشف الشبكة مع كل طبقة وظائف أعلى وأكثر تجريدية.

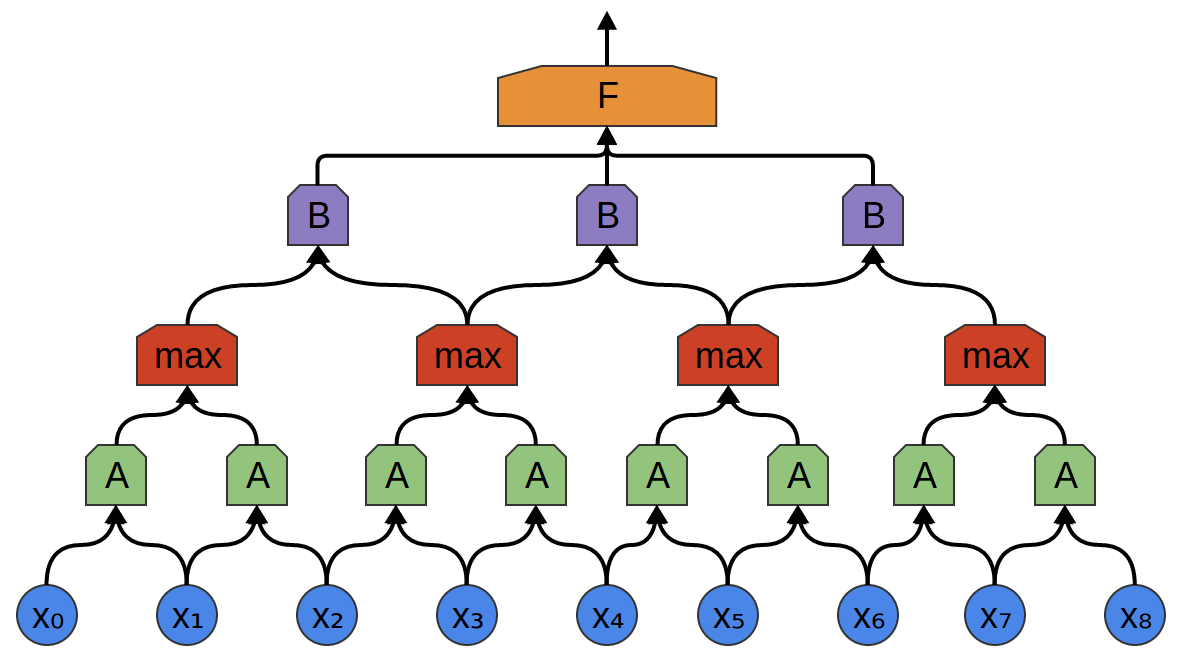
في المثال التالي ، هناك مجموعة جديدة من الخلايا العصبية B. B تستخدم لإنشاء طبقة تلافيفية أخرى وضعت فوق الطبقة السابقة.



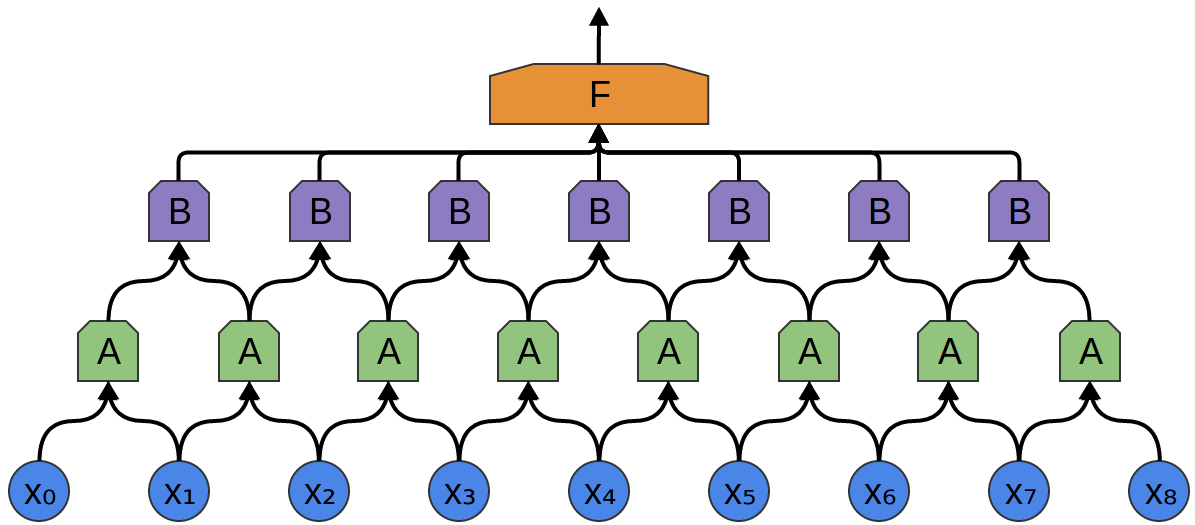
غالبًا ما تتشابك الطبقات التلافيفية عن طريق تجميع (دمج) الطبقات. على وجه الخصوص ، هناك نوع من الطبقات يسمى التجميع الأقصى ، والذي يحظى بشعبية كبيرة.

في كثير من الأحيان ، لا نهتم باللحظة الدقيقة التي تظهر فيها إشارة مفيدة في البيانات. إذا حدث تغيير في تردد الإشارة عاجلاً أم آجلاً ، فهل يهم؟

يمتص Max-pooling الميزات القصوى من الكتل الصغيرة من المستوى السابق. يقول الاستنتاج ما إذا كانت إشارة الوظيفة المطلوبة موجودة في الطبقة السابقة ، ولكن ليس بالضبط أين.

طبقات التجميع القصوى - هذا "انخفاض". يسمح للطبقات التلافيفية اللاحقة بالعمل على أجزاء كبيرة من البيانات ، لأن البقع الصغيرة بعد طبقة الدمج تتوافق مع الرقعة الأكبر أمامها. كما أنها تجعلنا ثابتًا في بعض تحويلات البيانات الصغيرة جدًا.



في أمثلةنا السابقة ، تم استخدام طبقات تلافيفية أحادية البعد. ومع ذلك ، يمكن أن تعمل الطبقات التلافيفية مع بيانات أكثر ضخامة. في الواقع ، تستخدم أشهر الحلول المستندة إلى الشبكات العصبية التلافيفية الشبكات العصبية التلافيفية ثنائية الأبعاد للتعرف على الأنماط.



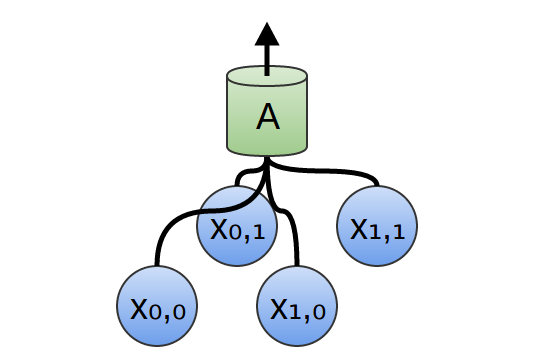
في طبقة تلافيفية ثنائية الأبعاد ، بدلاً من النظر إلى المقاطع ، سينظر A في البقع.

لكل رقعة ، تحسب A الوظيفة. على سبيل المثال ، يمكنها تعلم اكتشاف وجود حافة أو ملمس أو التباين بين لونين.



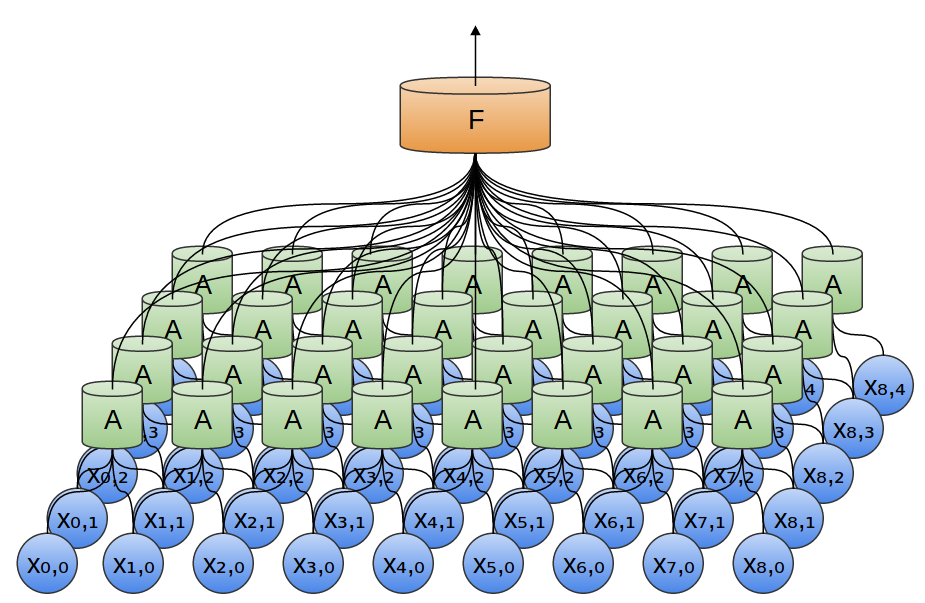
في المثال السابق ، تم إدخال ناتج الطبقة التلافيفية في طبقة متصلة بالكامل. ولكن ، من الممكن تكوين طبقتين تلافيفيتين ، كما كان الحال في الحالة ذات البعد الواحد.



يمكننا أيضًا إجراء التجميع الأقصى في بعدين. هنا نأخذ الحد الأقصى من الميزات من رقعة صغيرة.

هذا يتلخص في حقيقة أنه عند النظر في الصورة بأكملها ، فإن الوضع الدقيق للحافة ، حتى البكسل ، ليس مهمًا. يكفي أن تعرف مكانها في غضون بضع وحدات بكسل.



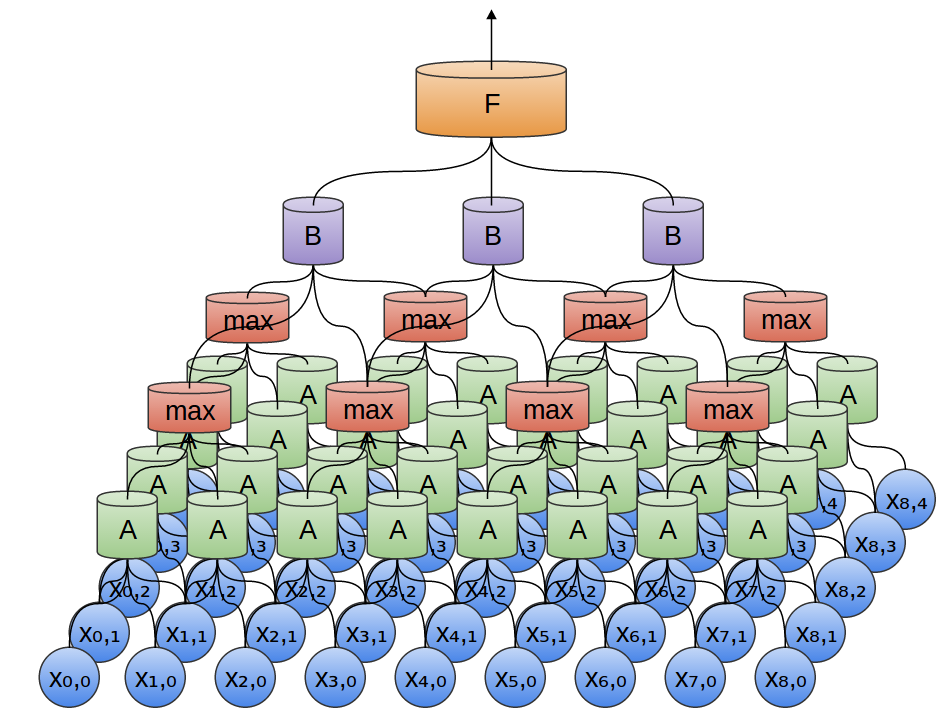
أيضًا ، تُستخدم شبكات الالتفاف ثلاثية الأبعاد أحيانًا لبيانات مثل الفيديو أو البيانات المجمعة (على سبيل المثال ، المسح ثلاثي الأبعاد في الطب). ومع ذلك ، لا يتم استخدام هذه الشبكات على نطاق واسع ، وأكثر صعوبة في التصور.

قلنا سابقًا أن A هي مجموعة من الخلايا العصبية. سنكون أكثر دقة في ذلك: ما هو A؟
في الطبقات التلافيفية التقليدية ، A هي مجموعة متوازية من الخلايا العصبية ، تتلقى جميع الخلايا العصبية نفس إشارات الإدخال وتحسب وظائف مختلفة.

على سبيل المثال ، في طبقة تلافيفية ثنائية الأبعاد ، يمكن لخلايا عصبية واحدة أن تكتشف الحواف الأفقية ، وأخرى ، والحواف الرأسية ، والتباين بين اللونين الأخضر والأحمر.



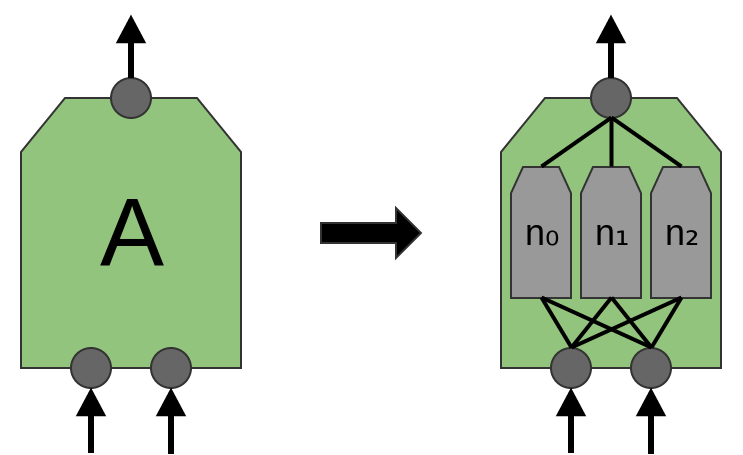
يقترح مقال "Network in Network" (لين وآخرون (2013)) طبقة جديدة ، "Mlpconv". في هذا النموذج ، تحتوي A على عدة مستويات من الخلايا العصبية ، حيث تستمد الطبقة الأخيرة وظائف مستوى أعلى للمنطقة التي يتم علاجها. في المقالة ، يحقق النموذج نتائج مبهرة ، ويحدد مستوى جديدًا من التكنولوجيا في عدد من مجموعات البيانات المرجعية.



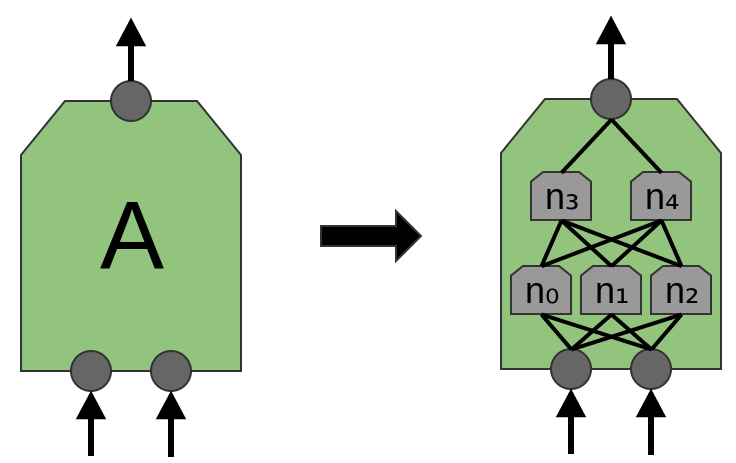
لأغراض هذا المنشور ، سنركز على طبقات تلافيفية قياسية.

نتائج الشبكة العصبية التلافيفية

في عام 2012 ، حقق Alex Krizhevsky و Ilya Sutskever و Geoff Hinton تحسنًا كبيرًا في جودة الاعتراف مقارنة بالحلول المعروفة في ذلك الوقت (Krizehvsky et al. (2012)).

كان التقدم نتيجة الجمع بين عدة مناهج. تم استخدام معالجات الرسوم لتدريب شبكة عصبية عميقة كبيرة (وفقًا لمعايير عام 2012). تم استخدام نوع جديد من الخلايا العصبية (ReLU) وتقنية جديدة لتقليل المشكلة تسمى "overfitting" (DropOut). استخدمنا مجموعة بيانات كبيرة مع عدد كبير من فئات الصور (ImageNet). وبالطبع كانت شبكة عصبية تلافيفية.
العمارة المبينة أدناه كانت عميقة. يحتوي على 5 طبقات تلافيفية ، 3 تجميع متناوب وثلاث طبقات متصلة بالكامل.



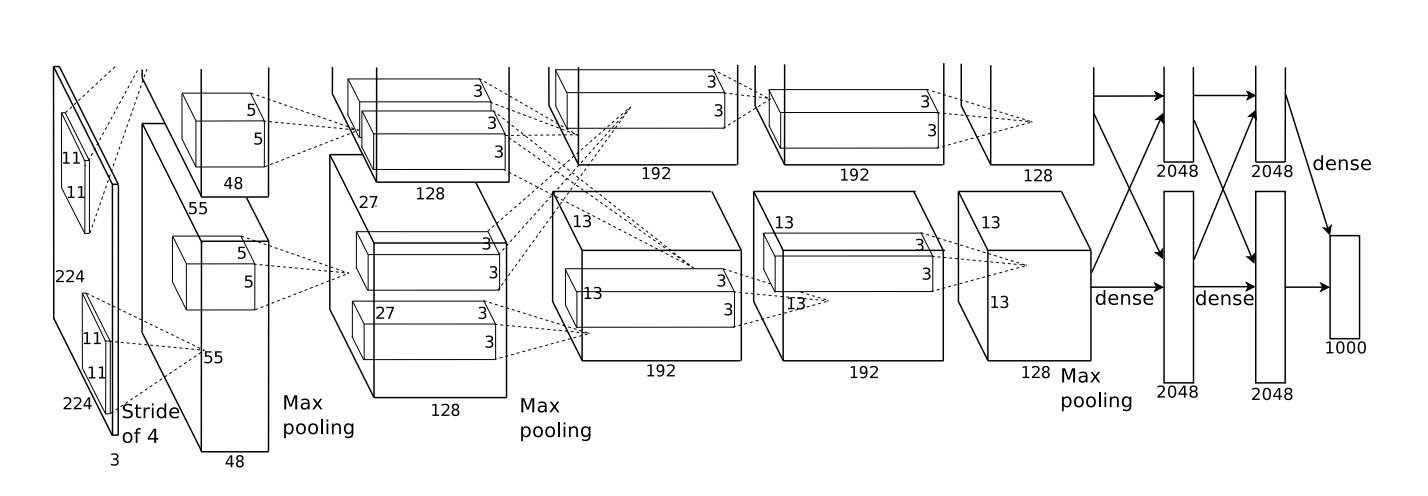
من كريزيفسكي وآخرون. (2012)
تم تدريب الشبكة على تصنيف الصور إلى آلاف الفئات المختلفة.

استطاع نموذج Krizhevsky وآخرون إعطاء الإجابة الصحيحة في 63٪ من الحالات. بالإضافة إلى ذلك ، الجواب الصحيح من أفضل 5 إجابات ، هناك 85 ٪ من التوقعات!



دعونا نوضح ما يعترف به المستوى الأول من الشبكة.

تذكر أنه تم تقسيم الطبقات التلافيفية بين وحدتي GPU. لا تنتقل المعلومات ذهابًا وإيابًا عبر كل طبقة. اتضح أنه في كل مرة يبدأ النموذج ، يتخصص كلا الجانبين.



المرشحات التي تم الحصول عليها من الطبقة التلافيفية الأولى. يتوافق النصف العلوي مع طبقة على وحدة معالجة رسومات واحدة ، والنصف السفلي على الآخر. من كريزيفسكي وآخرون. (2012)
تركز الخلايا العصبية على جانب واحد على الأسود والأبيض ، وتتعلم كيفية اكتشاف حواف الاتجاهات والأحجام المختلفة. من ناحية أخرى ، تتخصص الخلايا العصبية في اللون والملمس ، وتكتشف تباينات وأنماط الألوان. تذكر أن الخلايا العصبية تتم تهيئتها بشكل عشوائي. لم يذهب أي شخص لتعيينهم ككاشفات للحدود أو تقسيمهم بهذه الطريقة. حدث هذا أثناء تدريب شبكة تصنيف الصور.

كانت هذه النتائج الرائعة (وغيرها من النتائج المثيرة حول الوقت) مجرد البداية. وقد تبعهم بسرعة العديد من الأعمال الأخرى التي اختبرت النهج المعدلة وحسنت النتائج تدريجياً أو طبقتها في مجالات أخرى.
الشبكات العصبية التلافيفية أداة مهمة في رؤية الكمبيوتر والتعرف على الأنماط الحديثة.

إضفاء الطابع الرسمي على الشبكات العصبية التلافيفية

خذ بعين الاعتبار طبقة تلافيفية أحادية البعد مع المدخلات {xn} والمخرجات {yn}:



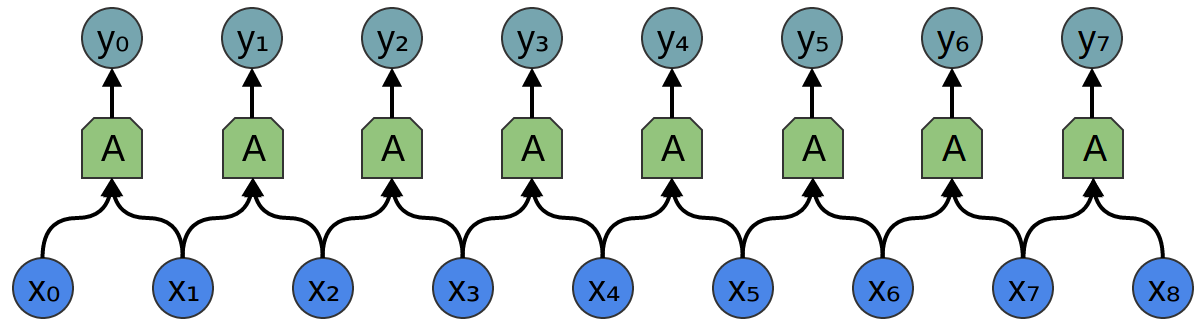
من السهل نسبيًا وصف النتائج من حيث المدخلات:

yn = A (x، x + 1، ...)

على سبيل المثال ، في المثال أعلاه:

y0 = A (x0، x1)
y1 = A (x1، x2)

وبالمثل ، إذا أخذنا في الاعتبار طبقة تلافيفية ثنائية الأبعاد ذات مدخلات {xn، m} ومخرجات {yn، m}:



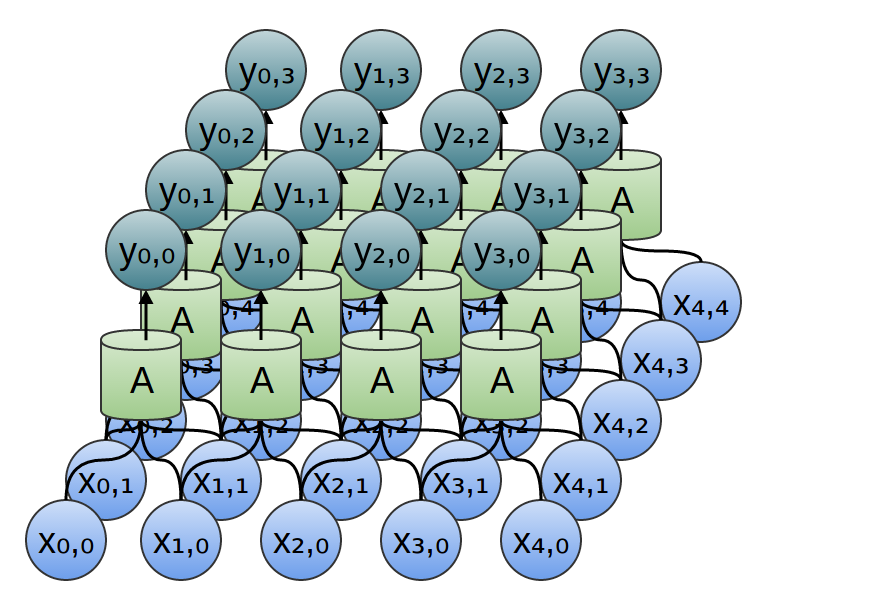
يمكن تمثيل الشبكة بمصفوفة ثنائية الأبعاد من القيم.

الخلاصة

عملية الالتفاف أداة قوية. في الرياضيات ، تنشأ عملية الالتفاف في سياقات مختلفة ، من دراسة المعادلات التفاضلية الجزئية إلى نظرية الاحتمالات. يرجع جزء من دوره في PDE إلى أن الالتفاف مهم في العلوم الفيزيائية. يلعب الالتفاف أيضًا دورًا مهمًا في العديد من مجالات التطبيق ، مثل رسومات الكمبيوتر ومعالجة الإشارات.