لسنوات عديدة كنت أشاهد السنوكر كرياضة. لديها كل شيء: الجمال الفاتن للعبة الفكرية ، وأناقة ضربات كيم والتوتر النفسي للمنافسة. ولكن هناك شيء واحد لا يعجبني - نظام التصنيف الخاص به .
عيبه الرئيسي هو أنه يأخذ في الاعتبار فقط حقيقة إنجاز البطولة دون مراعاة "تعقيد" المباريات. إن نموذج Elo محروم من هذا العيب ، الذي يراقب "قوة" اللاعبين ويحدثها اعتمادًا على نتائج المباريات و "قوة" الخصم. ومع ذلك ، فإنه لا يتناسب تمامًا: من المعتقد أن جميع المباريات تقام في ظروف متساوية ، وفي السنوكر يتم لعبها إلى عدد معين من الإطارات (الأطراف) الفائزة. ولأخذ هذه الحقيقة بعين الاعتبار ، فكرت في نموذج آخر ، أطلقت عليه اسم EloBeta .
تدرس هذه المقالة جودة طرز Elo و EloBet استنادًا إلى نتائج مباريات السنوكر. من المهم أن نلاحظ أن الأهداف الرئيسية هي تقييم "قوة" اللاعبين وإنشاء تصنيف "عادل" ، بدلاً من بناء نماذج تنبؤية لتحقيق الربح.

يعتمد تصنيف السنوكر الحالي على إنجازات اللاعب في البطولات مع "وزنه" المختلف. ذات مرة ، تم أخذ بطولات العالم فقط في الاعتبار. بعد ظهور العديد من المسابقات الأخرى ، تم تطوير جدول نقاط يمكن للاعب أن يكسبه عندما وصل إلى مرحلة معينة من البطولة. أصبح التقييم الآن على شكل مبلغ "متحرك" من أموال الجائزة التي كسبها اللاعب خلال العامين التقويميين (تقريبًا).
يحتوي هذا النظام على ميزتين رئيسيتين: إنه بسيط (اربح الكثير من المال - صعد في الترتيب) وقابل للتنبؤ (إذا كنت تريد الصعود إلى مكان معين - اربح مبلغًا معينًا من المال ، وكل الأشياء الأخرى متساوية). المشكلة هي أنه بهذه الطريقة لا تؤخذ في الاعتبار قوة (مهارة ، شكل) الخصوم . الحجة المضادة المعتادة هي: "إذا وصل اللاعب إلى المرحلة المتأخرة من البطولة ، فهو / ها هو اللاعب القوي الحالي" ("اللاعبون الضعفاء لا يفوزون بالبطولات"). تبدو مقنعة للغاية. ومع ذلك ، في لعبة السنوكر ، كما هو الحال في أي رياضة ، يجب أن يؤخذ دور القضية في الاعتبار: إذا كان اللاعب "أضعف" ، فهذا لا يعني أنه لن يتمكن أبدًا من الفوز "أقوى" في مباراة ضد لاعب. يحدث ذلك في كثير من الأحيان أقل من السيناريو العكسي. هذا هو المكان الذي يأتي فيه نموذج Elo إلى المشهد.
فكرة نموذج Elo هي أن كل لاعب مرتبط بتصنيف رقمي. تم تقديم افتراض بأن نتيجة لعبة بين لاعبين يمكن توقعها بناءً على الاختلاف في تقييماتهم: القيم الأعلى تعني احتمال أعلى للفوز بلاعب "قوي" (مع تصنيف أعلى). يعتمد تصنيف Elo على "القوة" الحالية ، المحسوبة على أساس نتائج المباريات مع لاعبين آخرين. هذا يتجنب وجود خلل كبير في نظام التصنيف الرسمي الحالي. يسمح لك هذا النهج أيضًا بتحديث تقييم اللاعب أثناء البطولة من أجل الاستجابة عدديًا لأدائه الجيد.
لديه خبرة عملية في تصنيف Elo ، يبدو لي أنه يجب أن يظهر نفسه جيدًا في لعبة السنوكر. ومع ذلك ، هناك عقبة واحدة: وهي مصممة للمسابقات بنوع واحد من المباريات . بالطبع ، هناك اختلافات لتأخذ في الاعتبار مزايا الملعب المحلي في كرة القدم والحركة الأولى في الشطرنج (سواء في شكل إضافة عدد ثابت من نقاط التصنيف للاعب مع ميزة). في لعبة السنوكر ، يتم لعب المباريات بصيغة "الأفضل من N": اللاعب الذي يفوز في أول فوز n = f r a c N + 1 2 إطارات (الأطراف). وسنسمي هذا التنسيق أيضًا "حتى ن الانتصارات ".
بشكل حدسي ، يجب أن يكون الفوز بمباراة تصل إلى 10 انتصارات (نهائي بطولة خطيرة) أكثر صعوبة بالنسبة للاعب "الضعيف" من الفوز في مباراة 4 انتصارات (الجولة الأولى من بطولات الأمم المحلية الحالية). يؤخذ هذا في الاعتبار في نموذج EloBet الخاص بي.
إن فكرة استخدام تصنيف Elo في لعبة السنوكر ليست جديدة بأي حال من الأحوال. على سبيل المثال ، هناك الأعمال التالية:
- يستخدم محلل Snooker نظام تصنيف "Elo like" (يشبه إلى حد كبير نموذج Bradley - Terry ). الفكرة هي تحديث التصنيف بناءً على الفرق بين عدد الإطارات "الحقيقية" و "المتوقعة" التي تم ربحها. هذا النهج يثير تساؤلات. بالطبع ، فإن الاختلاف الأكبر في عدد الإطارات يرجح على الأرجح الفرق الأكبر في القوة ، ولكن في البداية لم يكن لدى اللاعب مثل هذه المهمة. في لعبة السنوكر ، الهدف هو "فقط" للفوز بالمباراة ، أي اربح عددًا معينًا من الإطارات قبل الخصم.
- هذه المناقشة في المنتدى مع تنفيذ نموذج Elo الأساسي.
- هذا وهذه هي الاستخدامات الحقيقية في لعبة السنوكر للهواة.
- ربما هناك أعمال أخرى فاتني. سأكون ممتنا للغاية لأية معلومات حول هذا الموضوع.
مراجعة
هذه المقالة مخصصة لمستخدمي لغة R المهتمين بدراسة تصنيف Elo ، ولعشاق لعبة السنوكر. تتم كتابة جميع التجارب بفكرة أن تكون قابلة للتكرار. الرمز مخفي تحت المفسدين ، ولديه تعليقات ويستخدم حزم tidyverse ، لذلك يمكن أن يكون من المثير للاهتمام للمستخدمين أن يقرؤوا وحدهم R. من المفترض أن يتم تنفيذ جميع التعليمات البرمجية بالتسلسل. يمكن العثور على ملف واحد هنا .
تم تنظيم المقال على النحو التالي:
- يصف قسم النموذج نهج Elo و EloBet مع التنفيذ في R.
- يصف قسم التجربة تفاصيل ودوافع الحساب: ما هي البيانات والمنهجية المستخدمة (ولماذا) ، وما هي النتائج التي يتم الحصول عليها.
- يحتوي قسم دراسة ترتيب EloBet على نتائج تطبيق نموذج EloBet على بيانات السنوكر الحقيقية. سيكون أكثر اهتماما بعشاق السنوكر.
سنحتاج إلى التهيئة التالية.
كود التهيئة# suppressPackageStartupMessages(library(dplyr)) library(tidyr) library(purrr) # library(ggplot2) # suppressPackageStartupMessages(library(comperank)) theme_set(theme_bw()) # . . set.seed(20180703)
النماذج
يعتمد كلا النموذجين على الافتراضات التالية:
- هناك مجموعة ثابتة من اللاعبين الذين يجب تصنيفهم من "الأقوى" (المركز الأول) إلى "الأضعف" (المركز الأخير).
- الترتيب حسب اتحاد اللاعبين ط مع التصنيف العددي ص ط : رقم يمثل "قوة" اللاعب (القيمة الأعلى تعني لاعب أقوى).
- كلما زاد الاختلاف في التقييمات قبل المباراة ، قل احتمال فوز اللاعب "الضعيف" (مع تصنيف أقل).
- يتم تحديث التقييمات بعد كل مباراة بناءً على نتيجتها وتصنيفاتها قبلها.
- الانتصار على "أقوى" للخصم يجب أن يقترن بزيادة أكبر في التصنيف من الانتصار على "أضعف" الخصم. مع الهزيمة ، العكس هو الصحيح.
Elo
كود Elo النموذجي #' @details . #' `...` . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). #' . elo_win_prob <- function(rating1, rating2, ksi = 400, ...) { norm_rating_diff <- (rating2 - rating1) / ksi 1 / (1 + 10^norm_rating_diff) } #' @return , #' `comperank::add_iterative_ratings()`. elo_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { comperank::elo(rating1, score1, rating2, score2, K = K, ksi = ksi)[1, ] } }
يقوم Elo Model بتحديث التصنيفات من خلال الإجراء التالي:
حساب احتمالية فوز لاعب معين في المباراة (قبل أن تبدأ). احتمالية فوز لاعب واحد (سنطلق عليه "الأول") مع المعرف ط وقيم ص ط على لاعب آخر ("الثاني") بمعرف ي وقيم ص ي يساوي
P r ( r i ، r j ) = f r a c 1 1 + 10 ( r j - r i ) / 400
مع هذا النهج ، يحسب حساب الاحتمالية الافتراض الثالث.
إن تسوية الفرق إلى 400 طريقة رياضية لقول أي اختلاف يعتبر "كبيرًا". يمكن استبدال هذا الرقم بمعلمة نموذج. س ط ومع ذلك ، فإن هذا يؤثر فقط على انتشار التصنيفات المستقبلية وعادة ما تكون زائدة عن الحاجة. قيمة 400 قياسية إلى حد ما.
مع نهج عام ، فإن احتمال النصر يساوي L ( ص ي - ص ط ) أين L ( خ ) بعض الوظائف المتزايدة بشكل صارم مع القيم من 0 إلى 1. سوف نستخدم المنحنى اللوجستي. يمكن العثور على دراسة أكثر اكتمالا في هذه المقالة .
حساب نتيجة المباراة ق . في النموذج الأساسي ، يساوي 1 في حالة فوز اللاعب الأول (هزيمة اللاعب الثاني) ، 0.5 في حالة التعادل و 0 في حالة هزيمة اللاعب الأول (انتصار اللاعب الثاني).
تحديث التصنيف :
- delta=K cdot(S−Pr(ri،rj)) . هذا هو المبلغ الذي ستتغير به التصنيفات. تستخدم معامل K (المعلمة الوحيدة للنموذج). أقل K (مع احتمالات متساوية) يعني تغييرًا أصغر في التصنيفات - النموذج أكثر تحفظًا ، أي هناك حاجة لمزيد من الانتصارات من أجل "إثبات" تغيير في القوة. من ناحية أخرى ، أكثر K يعني المزيد من المصداقية مع النتائج الأخيرة من التصنيفات الحالية. اختيار "الأمثل" K هي طريقة لإنشاء نظام تصنيف "جيد" .
- r(جديد)i=ri+ delta ، r(جديد)j=rj− delta .
ملاحظات :
- كما يتضح من صيغ التحديث ، لا يتغير مجموع تقييمات جميع اللاعبين المعتبرين بمرور الوقت: يزيد التصنيف بسبب انخفاض في تصنيف الخصم
- ويرتبط اللاعبون الذين لم يلعبوا مباريات بتصنيف مبدئي قدره 0. وعادة ما يتم استخدام قيم 1500 أو 1000 ، لكني لا أرى أي سبب آخر غير نفسي. مع الأخذ في الاعتبار الملاحظة السابقة ، فإن استخدام الصفر يعني أن مجموع جميع التقييمات هو صفر دائمًا ، وهو جميل بطريقته الخاصة.
- من الضروري لعب عدد معين من المباريات لكي يعكس التصنيف "قوة" اللاعب. هذا يمثل مشكلة: يبدأ اللاعبون المضافون حديثًا بتصنيف 0 ، وهو على الأرجح ليس الأصغر بين اللاعبين الحاليين. وبعبارة أخرى ، يعتبر "الوافدون الجدد" "أقوى" من بعض اللاعبين الآخرين. يمكنك محاولة محاربة هذا بإجراءات تحديث التصنيف الخارجية عند دخول لاعب جديد.
لماذا هذه الخوارزمية منطقية؟ في حالة تساوي الدرجات delta يساوي دائما 0.5 cdotK . لنفترض ، على سبيل المثال ، أن ri=0 و rj=400 . هذا يعني أن احتمال فوز اللاعب الأول هو frac11+10 حوالي0.0909 ، أي سيفوز في مباراة واحدة من أصل 11.
- في حالة الانتصار ، سيحصل على زيادة تقريبية
 وهو أكثر مما في حالة تساوي التصنيفات.
وهو أكثر مما في حالة تساوي التصنيفات. - في حالة الهزيمة ، سيحصل على تخفيض قدره تقريبًا
 وهو أقل مما في حالة المساواة في التصنيفات.
وهو أقل مما في حالة المساواة في التصنيفات.
هذا يدل على أن نموذج Elo يطيع الافتراض الخامس: الانتصار على الخصم "أقوى" مصحوبًا بزيادة أكبر في التصنيف من الانتصار على الخصم هو "أضعف" ، والعكس صحيح.
بالطبع ، يتميز نموذج Elo بميزاته العملية (عالية المستوى). ومع ذلك ، فإن الأهم بالنسبة لدراستنا هو ما يلي: من المفترض أن جميع المباريات تقام على قدم المساواة. هذا يعني أن مسافة المباراة لا تؤخذ بعين الاعتبار: الفوز في مباراة تصل إلى 4 انتصارات يكافأ بنفس الطريقة التي يفوز بها الفوز في مباراة تصل إلى 10 انتصارات. هنا يأتي نموذج المرحلة EloBeta.
EloBeta
رمز EloBet النموذجي #' @details . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). `frames_to_win` #' . #' . elobeta_win_prob <- function(rating1, rating2, frames_to_win, ksi = 400, ...) { prob_frame <- elo_win_prob(rating1 = rating1, rating2 = rating2, ksi = ksi) # , `frames_to_win` # # (`prob_frame`). . pbeta(prob_frame, frames_to_win, frames_to_win) } #' @return : 1 / #' (), 0.5 0 / (). get_match_result <- function(score1, score2) { # () , . near_score <- dplyr::near(score1, score2) dplyr::if_else(near_score, 0.5, as.numeric(score1 > score2)) } #' @return , #' `add_iterative_ratings()`. elobeta_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { prob_win <- elobeta_win_prob( rating1 = rating1, rating2 = rating2, frames_to_win = pmax(score1, score2), ksi = ksi ) match_result <- get_match_result(score1, score2) delta <- K * (match_result - prob_win) c(rating1 + delta, rating2 - delta) } }
في نموذج Elo ، يؤثر الفرق في التصنيفات بشكل مباشر على احتمالية الفوز في المباراة بأكملها. الفكرة الرئيسية لنموذج EloBet هي التأثير المباشر للاختلاف في التصنيفات على احتمالية الفوز في إطار واحد والحساب الصريح لاحتمال فوز اللاعب n الإطارات قبل الخصم .
يبقى السؤال: كيف نحسب مثل هذا الاحتمال؟ اتضح أن هذه واحدة من أقدم المشاكل في تاريخ نظرية الاحتمالات ولها اسمها الخاص - مشكلة تقسيم الرهانات (مشكلة النقاط). يمكن العثور على عرض جيد للغاية في هذه المقالة . باستخدام ترميزها ، فإن الاحتمال المطلوب هو:
P(n،n)= sum limits2n−1j=n2n−1 اختيارjpj(1−p)2n−1−j
هنا P(n،n) - احتمالية فوز اللاعب الأول بالمباراة من قبل n انتصارات p - احتمالية انتصاره في إطار واحد (احتمال الخصم 1−p ) مع هذا النهج ، يفترض أن نتائج الإطار داخل المباراة مستقلة عن بعضها البعض . قد يكون هذا موضع شك ، ولكنه افتراض ضروري لهذا النموذج.
هل هناك طريقة أسرع للحساب؟ اتضح أن الإجابة هي نعم. بعد عدة ساعات من تحويل الصيغة والتجارب العملية وعمليات البحث على الإنترنت ، وجدت الخاصية التالية في وظيفة بيتا غير مكتملة ومنتظمة Ix(a،b) . الاستبدال m=k، n=2k−1 في هذه الخاصية واستبدالها k على n اتضح P(n،n)=Ip(n،n) .
هذه أيضا أخبار جيدة لمستخدمي R ، مثل Ip(n،n) يمكن حسابها على أنها pbeta(p, n, n) . ملحوظة : الحالة العامة لاحتمال النصر في n الإطارات قبل فوز الخصم م يمكن أيضا حسابها Ip(n،m) pbeta(p, n, m) على التوالي. هذا يفتح فرصًا كبيرة لتحديث احتمالية الفوز خلال المباراة .
يحتوي إجراء تحديث التصنيف في إطار نموذج EloBet على النموذج التالي (مع تقييمات معروفة ri و rj عدد الإطارات المطلوبة للفوز n ونتيجة المباراة S ، كما في نموذج Elo):
- حساب احتمالية فوز اللاعب الأول في إطار واحد : p=Pr(ri،rj)= frac11+10(rj−ri)/400 .
- حساب احتمالية فوز هذا اللاعب في المباراة : PrBeta(ri،rj)=Ip(n،n) . على سبيل المثال ، إذا p يساوي 0.4 ، ثم ينخفض احتمال الفوز في المباراة قبل 4 انتصارات إلى 0.29 ، وفي "إلى 18 انتصارا" - إلى 0.11.
- تحديث التصنيف :
- delta=K cdot(S−PrBeta(ri،rj)) .
- r(جديد)i=ri+ delta ، r(جديد)j=rj− delta .
ملاحظة : لأن يؤثر الفرق في التصنيفات بشكل مباشر على احتمالية الفوز في إطار واحد ، وليس في المباراة بأكملها ، يجب توقع قيمة معامل أفضل K : جزء من القيمة delta يأتي من تأثير التعزيز PrBeta(ri،rj) .
إن فكرة حساب نتيجة المباراة بناءً على احتمال الفوز في إطار واحد ليست جديدة للغاية. في هذا الموقع الخاص بتأليف François Labelle ، يمكنك العثور على حساب عبر الإنترنت لاحتمال الفوز "بأفضل N "المباراة ، جنبًا إلى جنب مع الوظائف الأخرى. لقد أسعدني أن أرى أن نتائج الحساب لدينا تتطابق. ومع ذلك ، لم أتمكن من العثور على أي مصادر لإدخال مثل هذا النهج في إجراء التحديث لتصنيفات Elo. كما كان من قبل ، سأكون ممتنًا جدًا لأية معلومات حول هذا الموضوع.
لم أجد سوى هذه المقالة ووصف نظام Elo على خادم لعبة الطاولة (FIBS). هناك أيضا نظير باللغة الروسية . هنا ، يتم أخذ فترات المطابقة المختلفة في الاعتبار عن طريق ضرب الفرق في التصنيفات بالجذر التربيعي لمسافة المطابقة. ومع ذلك ، لا يبدو أن لديها أي مبرر نظري.
تجربة
للتجربة عدة أهداف. بناء على نتائج مباريات السنوكر:
- حدد أفضل قيم المعامل K لكلا النموذجين.
- دراسة استقرار النماذج من حيث دقة الاحتمالية التنبؤية.
- دراسة أثر استخدام بطولات "الدعوة" على التصنيفات.
- قم بإنشاء سجل تقييم عادل لموسم 2017/18 لجميع اللاعبين المحترفين.
البيانات
رمز إنشاء بيانات التجربة # "train", "validation" "test" split_cases <- function(n, props = c(0.5, 0.25, 0.25)) { breaks <- n * cumsum(head(props, -1)) / sum(props) id_vec <- findInterval(seq_len(n), breaks, left.open = TRUE) + 1 c("train", "validation", "test")[id_vec] } pro_players <- snooker_players %>% filter(status == "pro") # pro_matches_all <- snooker_matches %>% # filter(!walkover1, !walkover2) %>% # semi_join(y = pro_players, by = c(player1Id = "id")) %>% semi_join(y = pro_players, by = c(player2Id = "id")) %>% # 'season' left_join( y = snooker_events %>% select(id, season), by = c(eventId = "id") ) %>% # arrange(endDate) %>% # widecr transmute( game = seq_len(n()), player1 = player1Id, score1, player2 = player2Id, score2, matchId = id, endDate, eventId, season, # ("train", "validation" "test") # 50/25/25 matchType = split_cases(n()) ) %>% # widecr as_widecr() # (, # , Championship League). pro_matches_off <- pro_matches_all %>% anti_join( y = snooker_events %>% filter(type == "Invitational"), by = c(eventId = "id") ) # get_split <- . %>% count(matchType) %>% mutate(share = n / sum(n)) # 50/25/25 (train/validation/test) pro_matches_all %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 1030 0.250 ## 2 train 2059 0.5 ## 3 validation 1029 0.250 # , # . , # __ __, `pro_matches_all`. # , __ # __. pro_matches_off %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 820 0.225 ## 2 train 1810 0.497 ## 3 validation 1014 0.278 # K k_grid <- 1:100
سنستخدم بيانات السنوكر من حزمة الشركة. المصدر الأصلي هو snooker.org . النتائج مأخوذة من المباريات التالية:
- تم لعب المباراة في موسم 2016/2017 أو 2017/18 .
- المباراة هي جزء من بطولة سنوكر "محترفة" وهي:
- وهي من النوع "Invitational" أو "Qualification" أو "Ranking". سنميز أيضًا مجموعتين من المباريات: "جميع المباريات" (من جميع بيانات البطولة) و "المباريات الرسمية" (باستثناء بطولات الدعوة). هناك سببان لذلك:
- في بطولات الدعوة ، لا تتاح الفرصة لجميع اللاعبين لتغيير تصنيفهم. هذا ليس سيئًا بالضرورة في إطار نموذجي Elo و EloBet ، ولكن له "مسحة من الظلم".
- هناك اعتقاد بأن اللاعبين "يأخذون على محمل الجد" فقط لمباريات التصنيف الرسمي. ملحوظة : معظم البطولات الدعوية هي جزء من دوري البطولة ، والتي أعتقد أنها مقبولة من قبل معظم اللاعبين.
ليس على محمل الجد في شكل ممارسة مع القدرة على كسب المال. قد يؤثر وجود هذه البطولات على الترتيب. بالإضافة إلى "بطولة البطولة" ، هناك بطولات دعوة أخرى: "بطولة الصين 2016" ، كلاهما "بطل الأبطال" ، كلاهما "ماسترز" ، "هونغ كونغ ماسترز 2017" ، "2017 World Games" ، "2017 Roman Masters".
- يصف سنوكر تقليدي (ليس 6 ريدز أو باور سنوكر) بين لاعبين فرديين (وليس فرق).
- يمكن أن يكون كلا الجنسين متورطين (ليس فقط الرجال أو النساء).
- يمكن للاعبين من جميع الأعمار المشاركة (ليس فقط كبار السن أو "أقل من 21").
- هذا ليس "Shoot-Out" لأنه هذه البطولات مخزنة في قاعدة بيانات snooker.org.
- جرت المباراة حقًا : النتيجة هي نتيجة مباراة حقيقية يشارك فيها كلا اللاعبين.
- تقام المباراة بين اثنين من المحترفين . يتم أخذ قائمة المحترفين لموسم 2017/18 (131 لاعبًا). يبدو أن هذا القرار هو الأكثر إثارة للجدل ، كما إزالة المباريات التي تنطوي على "الستائر" الهواة لهزيمة المهنيين من الهواة. هذا يؤدي إلى ميزة غير عادلة لهؤلاء اللاعبين. يبدو لي أن مثل هذا القرار ضروري للحد من تضخم التصنيف الذي سيحدث عند مراعاة المطابقات مع الهواة. نهج آخر هو دراسة المهنيين والهواة معًا ، ولكن هذا يبدو غير معقول في إطار هذه الدراسة. تعتبر هزيمة الهواة المحترفين خسارة فرصة لزيادة التصنيف.
العدد النهائي للمباريات المستخدمة هو 4118 لكل المباريات و 3644 للمباريات الرسمية (62.9 و 55.6 لكل لاعب على التوالي).
المنهجية
رمز وظيفة التجربة #' @param matches `longcr` `widecr` `matchType` #' ( : "train", "validation" "test"). #' @param test_type . #' #' ("") . , #' `game`. #' @param k_vec K . #' @param rate_fun_gen , K #' `add_iterative_ratings()`. #' @param get_win_prob #' (`rating1`, `rating2`) , #' (`frames_to_win`). ____: #' . #' @param initial_ratings #' `add_iterative_ratings()`. #' #' @details : #' - `matches` #' `game`. #' - `test_type`: #' - 1. #' - : 1 / #' (), 0.5 0 / (). #' - RMSE: , #' "" - . #' #' @return Tibble 'k' K 'goodness' #' RMSE. compute_goodness <- function(matches, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings = 0) { cat("\n") map_dfr(k_vec, function(cur_k) { # cat(cur_k, " ") matches %>% arrange(game) %>% add_iterative_ratings( rate_fun = rate_fun_gen(cur_k), initial_ratings = initial_ratings ) %>% left_join(y = matches %>% select(game, matchType), by = "game") %>% filter(matchType %in% test_type) %>% mutate( # framesToWin = pmax(score1, score2), # 1 `framesToWin` winProb = get_win_prob( rating1 = rating1Before, rating2 = rating2Before, frames_to_win = framesToWin ), result = get_match_result(score1, score2), squareError = (result - winProb)^2 ) %>% summarise(goodness = sqrt(mean(squareError))) }) %>% mutate(k = k_vec) %>% select(k, goodness) } #' `compute_goodness()` compute_goodness_wrap <- function(matches_name, test_type, k_vec, rate_fun_gen_name, win_prob_fun_name, initial_ratings = 0) { matches_tbl <- get(matches_name) rate_fun_gen <- get(rate_fun_gen_name) get_win_prob <- get(win_prob_fun_name) compute_goodness( matches_tbl, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings ) } #' #' #' @param test_type `test_type` ( ) #' `compute_goodness()`. #' @param rating_type ( ). #' @param data_type . #' @param k_vec,initial_ratings `compute_goodness()`. #' #' @details #' . #' , , #' : #' - "pro_matches_" + `< >` + `< >` . #' - `< >` + "_fun_gen" . #' - `< >` + "_win_prob" , #' . #' #' @return Tibble : #' - __testType__ <chr> : . #' - __ratingType__ <chr> : . #' - __dataType__ <chr> : . #' - __k__ <dbl/int> : K. #' - __goodness__ <dbl> : . do_experiment <- function(test_type = c("validation", "test"), rating_type = c("elo", "elobeta"), data_type = c("all", "off"), k_vec = k_grid, initial_ratings = 0) { crossing( testType = test_type, ratingType = rating_type, dataType = data_type ) %>% mutate( dataName = paste0("pro_matches_", testType, "_", dataType), kVec = rep(list(k_vec), n()), rateFunGenName = paste0(ratingType, "_fun_gen"), winProbFunName = paste0(ratingType, "_win_prob"), initialRatings = rep(list(initial_ratings), n()), experimentData = pmap( list(dataName, testType, kVec, rateFunGenName, winProbFunName, initialRatings), compute_goodness_wrap ) ) %>% unnest(experimentData) %>% select(testType, ratingType, dataType, k, goodness) }
"" K K=1,2,...,100 . , . :
- K :
- . , .
add_iterative_ratings() comperank . " ", .. . - , ( ) , . RMSE ( ) ( ). , RMSE=√1|T|∑t∈T(St−Pt)2 أين T — , |T| — , St — , Pt — ( ). , " " .
- K RMSE . "" , RMSE K ( ). 0.5 ( "" 0.5) .
, : "train" (), "validation" () "test" (). , .. "train"/"validation" , "validation"/"test". 50/25/25 " ". " " " " . : 49.7/27.8/22.5. , , .
:
- : .
- : " " " " ( ". ").
- : "" ( "validation" RMSE "" "train" ) "" ( "test" RMSE "" "train" "validation" ).
النتائج
pro_matches_validation_all <- pro_matches_all %>% filter(matchType != "test") pro_matches_validation_off <- pro_matches_off %>% filter(matchType != "test") pro_matches_test_all <- pro_matches_all pro_matches_test_off <- pro_matches_off
# experiment_tbl <- do_experiment()
plot_data <- experiment_tbl %>% unite(group, ratingType, dataType) %>% mutate( testType = recode( testType, validation = "", test = "" ), groupName = recode( group, elo_all = ", ", elo_off = ", . ", elobeta_all = ", ", elobeta_off = ", . " ), # groupName = factor(groupName, levels = unique(groupName)) ) compute_optimal_k <- . %>% group_by(testType, groupName) %>% slice(which.min(goodness)) %>% ungroup() compute_k_labels <- . %>% compute_optimal_k() %>% mutate(label = paste0("K = ", k)) %>% group_by(groupName) %>% # K , # . - # . mutate(hjust = - (k == max(k)) * 1.1 + 1.05) %>% ungroup() plot_experiment_results <- function(results_tbl) { ggplot(results_tbl) + geom_hline( yintercept = 0.5, colour = "#AA5555", size = 0.5, linetype = "dotted" ) + geom_line(aes(k, goodness, colour = testType)) + geom_vline( data = compute_optimal_k, mapping = aes(xintercept = k, colour = testType), linetype = "dashed", show.legend = FALSE ) + geom_text( data = compute_k_labels, mapping = aes(k, Inf, label = label, hjust = hjust), vjust = 1.2 ) + facet_wrap(~ groupName) + scale_colour_manual( values = c(`` = "#377EB8", `` = "#FF7F00"), guide = guide_legend(title = "", override.aes = list(size = 4)) ) + labs( x = " K", y = " (RMSE)", title = " ", subtitle = paste0( ' ( ) ', ' .\n', ' K ( ', '"") , .' ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_experiment_results(plot_data)
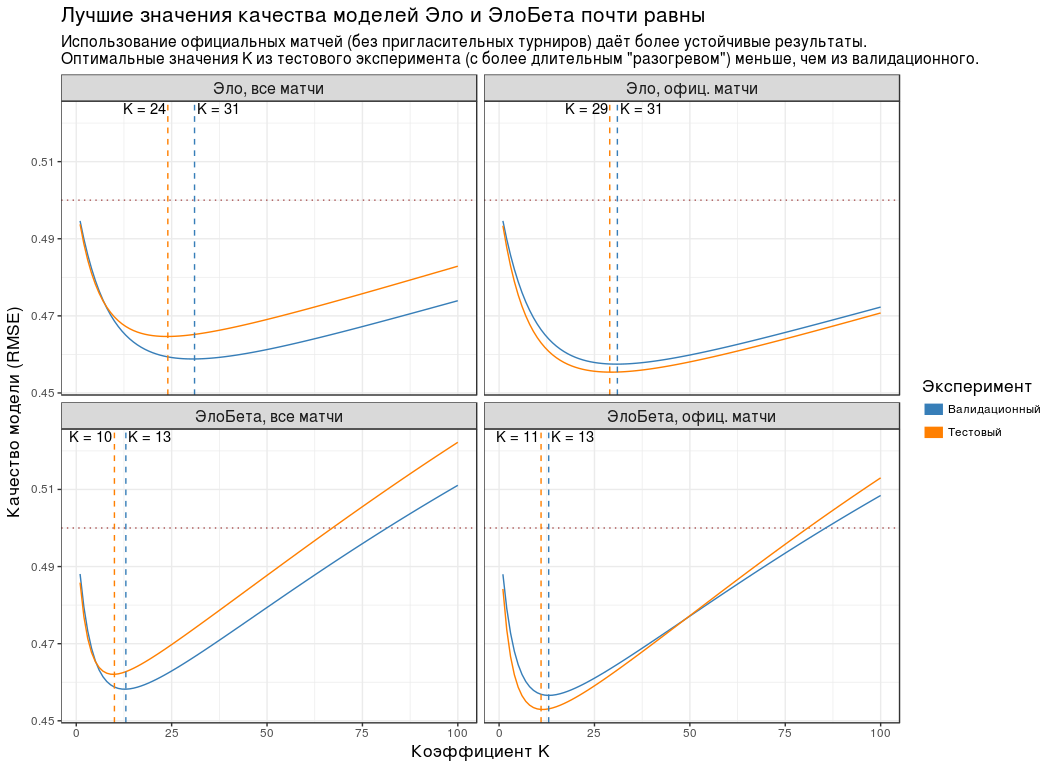
:
- , K , .
- ( "" "" ). , . - "Championship League": 3 .
- RMSE K . , RMSE K "" "". , " " .
- K ( "") , . "", .
- RMSE . 0.5. .
| K | RMSE |
|---|
| , | 24 | 0.465 |
| , . | التاسع والعشرون | 0.455 |
| , | 10 | 0.462 |
| , . | 11 | 0.453 |
لأن , K " " ( ) 5: 30, — 10.
, K=30 K=10 . , n , .
" " ( K=10 ) - .
-16 2017/18
-16 2017/18 # gather_to_longcr <- function(tbl) { bind_rows( tbl %>% select(-matches("2")) %>% rename_all(funs(gsub("1", "", .))), tbl %>% select(-matches("1")) %>% rename_all(funs(gsub("2", "", .))) ) %>% arrange(game) } # K best_k <- experiment_tbl %>% filter(testType == "test", ratingType == "elobeta", dataType == "off") %>% slice(which.min(goodness)) %>% pull(k) #!!! "" , .. !!! best_k <- round(best_k / 5) * 5 # elobeta_ratings <- rate_iterative( pro_matches_test_off, elobeta_fun_gen(best_k), initial_ratings = 0 ) %>% rename(ratingEloBeta = rating_iterative) %>% arrange(desc(ratingEloBeta)) %>% left_join( y = snooker_players %>% select(id, playerName = name), by = c(player = "id") ) %>% mutate(rankEloBeta = order(ratingEloBeta, decreasing = TRUE)) %>% select(player, playerName, ratingEloBeta, rankEloBeta) elobeta_top16 <- elobeta_ratings %>% filter(rankEloBeta <= 16) %>% mutate( rankChr = formatC(rankEloBeta, width = 2, format = "d", flag = "0"), ratingEloBeta = round(ratingEloBeta, 1) ) official_ratings <- tibble( player = c( 5, 1, 237, 17, 12, 16, 224, 30, 68, 154, 97, 39, 85, 2, 202, 1260 ), rankOff = c( 2, 3, 4, 1, 5, 7, 6, 13, 16, 10, 8, 9, 26, 17, 12, 23 ), ratingOff = c( 905750, 878750, 751525, 1315275, 660250, 543225, 590525, 324587, 303862, 356125, 453875, 416250, 180862, 291025, 332450, 215125 ) )
-16 2017/18 ( snooker.org):
| | | . | . | |
|---|
| Ronnie O'Sullivan | 1 | 128.8 | 2 | 905 750 | 1 |
| Mark J Williams | 2 | 123.4 | 3 | 878 750 | 1 |
| John Higgins | 3 | 112.5 | 4 | 751 525 | 1 |
| Mark Selby | 4 | 102.4 | 1 | 1 315 275 | -3 |
| Judd Trump | 5 | 92.2 | 5 | 660 250 | 0 |
| Barry Hawkins | 6 | 83.1 | 7 | 543 225 | 1 |
| Ding Junhui | 7 | 82.8 | 6 | 590 525 | -1 |
| Stuart Bingham | 8 | 74.3 | 13 | 324 587 | 5 |
| Ryan Day | 9 | 71.9 | 16 | 303 862 | 7 |
| Neil Robertson | 10 | 70.6 | 10 | 356 125 | 0 |
| Shaun Murphy | 11 | 70.1 | 8 | 453 875 | -3 |
| Kyren Wilson | 12 | 70.1 | 9 | 416 250 | -3 |
| Jack Lisowski | 13 | 68.8 | 26 | 180 862 | 13 |
| Stephen Maguire | 14 | 63.7 | 17 | 291 025 | 3 |
| Mark Allen | 15 | 63.7 | 12 | 332 450 | -3 |
| Yan Bingtao | 16 | 61.6 | 23 | 215 125 | 7 |
:
- №1 3 . , , ( ).
- "" ( 13 ), ( 7 ).
- 5 . , 6 - WPBSA. , - "" . : , — .
- .
- ( №11), (№14) (№15) -16. "" (№26), (№23) (№17).
. , №16 (Yan Bingtao) №1 (Ronnie O'Sullivan) 0.404. 4 0.299, " 10 " — 0.197 18 — 0.125. , .
# seasons_break <- ISOdatetime(2017, 5, 2, 0, 0, 0, tz = "UTC") # elobeta_history <- pro_matches_test_off %>% add_iterative_ratings(elobeta_fun_gen(best_k), initial_ratings = 0) %>% gather_to_longcr() %>% left_join(y = pro_matches_test_off %>% select(game, endDate), by = "game") # plot_all_elobeta_history <- function(history_tbl) { history_tbl %>% mutate(isTop16 = player %in% elobeta_top16$player) %>% ggplot(aes(endDate, ratingAfter, group = player)) + geom_step(data = . %>% filter(!isTop16), colour = "#C2DF9A") + geom_step(data = . %>% filter(isTop16), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_vline( xintercept = seasons_break, linetype = "dotted", colour = "#E41A1C", size = 1 ) + geom_text( x = seasons_break, y = Inf, label = " 2016/17", colour = "#E41A1C", hjust = 1.05, vjust = 1.2 ) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = paste0( " -16 2016/17" ), subtitle = paste0( " ", " ." ) ) + theme(title = element_text(size = 13)) } plot_all_elobeta_history(elobeta_history)
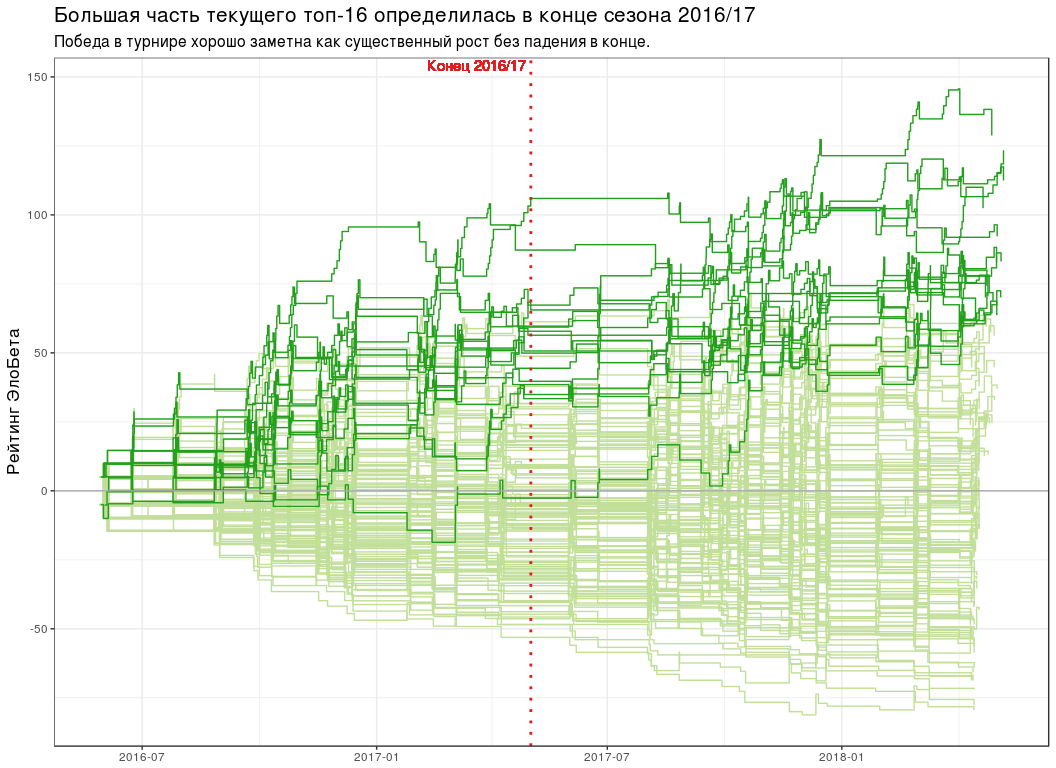
-16
-16 # top16_rating_evolution <- elobeta_history %>% # `inner_join` `elobeta_top16` inner_join(y = elobeta_top16 %>% select(-ratingEloBeta), by = "player") %>% # 2017/18 semi_join( y = pro_matches_test_off %>% filter(season == 2017), by = "game" ) %>% mutate(playerLabel = paste(rankChr, playerName)) # plot_top16_elobeta_history <- function(elobeta_history) { ggplot(elobeta_history) + geom_step(aes(endDate, ratingAfter, group = player), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_rug( data = elobeta_top16, mapping = aes(y = ratingEloBeta), sides = "r" ) + facet_wrap(~ playerLabel, nrow = 4, ncol = 4) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = " -16 ( 2017/18)", subtitle = paste0( " ' 2017/18.\n", " : 13- ." ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_top16_elobeta_history(top16_rating_evolution)
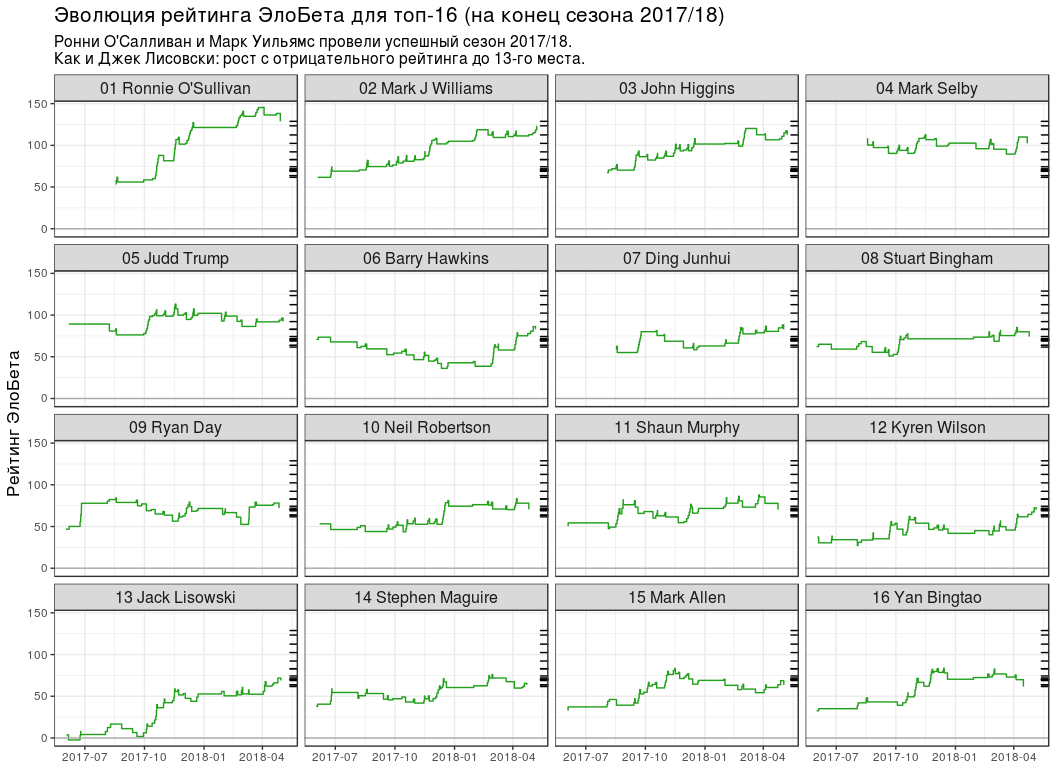
الاستنتاجات
- " " R :
pbeta(p, n, m) . - — "best of N " ( n ). .
- K=30 K=10 .
- :
sessionInfo() ## R version 3.4.4 (2018-03-15) ## Platform: x86_64-pc-linux-gnu (64-bit) ## Running under: Ubuntu 16.04.4 LTS ## ## Matrix products: default ## BLAS: /usr/lib/openblas-base/libblas.so.3 ## LAPACK: /usr/lib/libopenblasp-r0.2.18.so ## ## locale: ## [1] LC_CTYPE=ru_UA.UTF-8 LC_NUMERIC=C ## [3] LC_TIME=ru_UA.UTF-8 LC_COLLATE=ru_UA.UTF-8 ## [5] LC_MONETARY=ru_UA.UTF-8 LC_MESSAGES=ru_UA.UTF-8 ## [7] LC_PAPER=ru_UA.UTF-8 LC_NAME=C ## [9] LC_ADDRESS=C LC_TELEPHONE=C ## [11] LC_MEASUREMENT=ru_UA.UTF-8 LC_IDENTIFICATION=C ## ## attached base packages: ## [1] stats graphics grDevices utils datasets methods base ## ## other attached packages: ## [1] bindrcpp_0.2.2 comperank_0.1.0 comperes_0.2.0 ggplot2_2.2.1 ## [5] purrr_0.2.5 tidyr_0.8.1 dplyr_0.7.6 ## ## loaded via a namespace (and not attached): ## [1] Rcpp_0.12.17 knitr_1.20 bindr_0.1.1 magrittr_1.5 ## [5] munsell_0.5.0 tidyselect_0.2.4 colorspace_1.3-2 R6_2.2.2 ## [9] rlang_0.2.1 highr_0.7 plyr_1.8.4 stringr_1.3.1 ## [13] tools_3.4.4 grid_3.4.4 gtable_0.2.0 utf8_1.1.4 ## [17] cli_1.0.0 htmltools_0.3.6 lazyeval_0.2.1 yaml_2.1.19 ## [21] assertthat_0.2.0 rprojroot_1.3-2 digest_0.6.15 tibble_1.4.2 ## [25] crayon_1.3.4 glue_1.2.0 evaluate_0.10.1 rmarkdown_1.10 ## [29] labeling_0.3 stringi_1.2.3 compiler_3.4.4 pillar_1.2.3 ## [33] scales_0.5.0 backports_1.1.2 pkgconfig_2.0.1