"إن الهدف من هذه الدورة هو إعدادك لمستقبلك الفني."
مرحباً هابر. هل تتذكر المقالة الرائعة
"أنت وعملك
" (+219 ، 2442 إشارة مرجعية ، 394 ألف قراءة)؟
لذا فإن هامينغ (نعم ، نعم ، التدقيق الذاتي وتصحيح الذات
رموز الشفرات ) لديه
كتاب كامل مكتوب على أساس محاضراته. نحن نترجمها ، لأن الرجل يتحدث عن الأعمال.
هذا الكتاب لا يتعلق فقط بتكنولوجيا المعلومات ، إنه كتاب عن أسلوب التفكير لدى الأشخاص الرائعين بشكل لا يصدق.
"هذه ليست مجرد تهمة للتفكير الإيجابي ، يصف الظروف التي تزيد من فرص القيام بعمل عظيم ".لقد قمنا بالفعل بترجمة 28 فصلاً (من أصل 30).
ونحن نعمل على إصدار ورقي.
نظرية الترميز - أنا
بعد النظر في أجهزة الكمبيوتر ومبدأ عملها ، سننظر الآن في مسألة المعلومات: كيف تمثل أجهزة الكمبيوتر المعلومات التي نريد معالجتها. قد يعتمد معنى أي حرف على كيفية معالجته ، وليس للجهاز معنى محدد للبت المستخدم. عند مناقشة تاريخ البرنامج ، الفصل 4 ، أخذنا في الاعتبار بعض لغة البرمجة الاصطناعية ، حيث تزامن رمز تعليمات الفاصل مع رمز التعليمات الأخرى. هذا الوضع هو الحال بالنسبة لمعظم اللغات ، يتم تحديد معنى التعليمات من قبل البرنامج المقابل.
لتبسيط مشكلة تقديم المعلومات ، نعتبر مشكلة نقل المعلومات من نقطة إلى أخرى. يتعلق هذا السؤال بمسألة معلومات الحفظ. مشاكل نقل المعلومات في الزمان والمكان متطابقة. يوضح الشكل 10.1 نموذجًا قياسيًا لإرسال المعلومات.
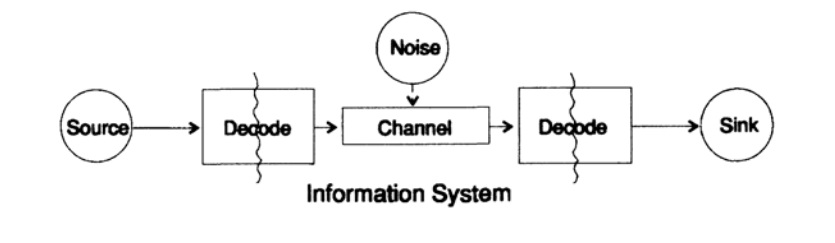الشكل 10.1على اليسار في الشكل 10.1 هو مصدر المعلومات. عند التفكير في النموذج ، لا نهتم بطبيعة المصدر. يمكن أن تكون مجموعة من رموز الأبجدية والأرقام والصيغ الرياضية والملاحظات الموسيقية والرموز التي يمكننا من خلالها تمثيل حركات الرقص - طبيعة المصدر ومعنى الرموز المخزنة فيه ليست جزءًا من نموذج الإرسال. نحن نعتبر مصدر المعلومات فقط ، مع هذا التقييد نحصل على نظرية عامة قوية يمكن توسيعها إلى العديد من المجالات. إنه تجريد من العديد من التطبيقات.
عندما أنشأ شانون نظرية المعلومات في نهاية الأربعينيات ، كان يعتقد أنه يجب أن يطلق عليها نظرية الاتصال ، لكنه أصر على مصطلح المعلومات. أصبح هذا المصطلح سببًا دائمًا لكل من الاهتمام المتزايد وخيبة الأمل المستمرة من الناحية النظرية. أراد المحققون بناء "نظريات معلومات" كاملة ، تحولوا إلى نظرية لمجموعة من الشخصيات. بالعودة إلى نموذج الإرسال ، لدينا مصدر بيانات يحتاج إلى ترميز للإرسال.
يتكون التشفير من جزأين ، الجزء الأول يسمى ترميز المصدر ، ويعتمد الاسم الدقيق على نوع المصدر. تتوافق مصادر أنواع البيانات المختلفة مع أنواع مختلفة من برامج التشفير.
الجزء الثاني من عملية التشفير يسمى ترميز القناة ويعتمد على نوع القناة لإرسال البيانات. وبالتالي ، فإن الجزء الثاني من عملية التشفير يتوافق مع نوع قناة الإرسال. وبالتالي ، عند استخدام الواجهات القياسية ، يتم ترميز البيانات من المصدر في البداية وفقًا لمتطلبات الواجهة ، ثم وفقًا لمتطلبات قناة البيانات المستخدمة.
وفقًا للنموذج ، في الشكل 10.1 ، تتعرض قناة البيانات إلى "ضوضاء عشوائية إضافية". يتم دمج كل الضوضاء في النظام عند هذه النقطة. يفترض أن المشفر يقبل جميع الأحرف دون تشويه ، ويقوم مفكك التشفير بوظيفته دون أخطاء. هذا هو بعض المثالية ، ولكن للعديد من الأغراض العملية فهو قريب من الواقع.
كما تتكون مرحلة فك التشفير من مرحلتين: قناة - قياسية - قياسية - مستقبل البيانات. في نهاية نقل البيانات إلى المستهلك. ومرة أخرى ، نحن لا نفكر في كيفية تفسير المستهلك لهذه البيانات.
كما ذكرنا سابقًا ، يقدم نظام إرسال البيانات ، على سبيل المثال ، الرسائل الهاتفية ، والإذاعة ، والبرامج التلفزيونية ، البيانات في شكل مجموعة من الأرقام في سجلات الكمبيوتر. أكرر مرة أخرى ، الإرسال في الفضاء لا يختلف عن الإرسال في الوقت أو تخزين المعلومات. هل لديك معلومات مطلوبة بعد فترة ، ثم يجب ترميزها وتخزينها على مصدر تخزين البيانات. إذا لزم الأمر ، يتم فك المعلومات. إذا كان نظام التشفير وفك التشفير هو نفسه ، فإننا ننقل البيانات عبر قناة الإرسال دون تغييرات.
الفرق الأساسي بين النظرية المقدمة والنظرية المعتادة في الفيزياء هو افتراض أنه لا يوجد ضوضاء في المصدر والمستقبل. في الواقع ، تحدث أخطاء في أي جهاز. في ميكانيكا الكم ، تحدث الضوضاء في أي مرحلة وفقًا لمبدأ عدم اليقين ، وليس كشرط أولي ؛ على أي حال ، فإن مفهوم الضجيج في نظرية المعلومات ليس معادلاً لمفهوم مماثل في ميكانيكا الكم.
من أجل التحديد ، سننظر أيضًا في الشكل الثنائي لتمثيل البيانات في النظام. تتم معالجة النماذج الأخرى بطريقة مماثلة ، من أجل البساطة لن نعتبرها.
نبدأ النظر في الأنظمة ذات الأحرف المشفرة ذات الطول المتغير ، كما هو الحال في شفرة مورس الكلاسيكية للنقاط والشرطات ، حيث تكون الأحرف التي تحدث بشكل متكرر قصيرة ونادرة طويلة. يتيح لك هذا النهج تحقيق كفاءة عالية في الشفرة ، ولكن تجدر الإشارة إلى أن شفرة مورس ثلاثية ، وليست ثنائية ، لأنها تحتوي على مسافة بين النقاط والشرطات. إذا كانت جميع الأحرف في الرمز بنفس الطول ، فإن هذا الرمز يسمى كود الكود.
أول خاصية ضرورية واضحة للشفرة هي القدرة على فك شفرة الرسالة بشكل فريد في حالة عدم وجود ضوضاء ، على الأقل يبدو أن هذه هي الخاصية المطلوبة ، على الرغم من أنه في بعض الحالات يمكن تجاهل هذا الشرط. تبدو البيانات من قناة الإرسال لجهاز الاستقبال بمثابة دفق من الأحرف من الأصفار والأرقام.
سوف نطلق على حرفين متجاورين امتدادًا مزدوجًا ، وثلاثة أحرف متجاورة امتدادًا ثلاثيًا ، وفي الحالة العامة ، إذا قمنا بإعادة توجيه أحرف N ، يرى المتلقي إضافات إلى الرمز الأساسي للحروف N. يجب على جهاز الاستقبال ، الذي لا يعرف قيمة N ، تقسيم التدفق إلى كتل البث. أو بعبارة أخرى ، يجب أن يكون جهاز الاستقبال قادرًا على تحليل الدفق بشكل فريد من أجل استعادة الرسالة الأصلية.
ضع في اعتبارك أبجدية لعدد صغير من الأحرف ، وعادة ما تكون الأبجدية أكبر بكثير. تبدأ أبجدية اللغات من 16 إلى 36 حرفًا ، بما في ذلك الأحرف الكبيرة والصغيرة ، وعلامات الأرقام ، وعلامات الترقيم. على سبيل المثال ، في جدول ASCII 128 = 2 ^ 7 أحرف.
ضع في اعتبارك رمزًا خاصًا يتكون من 4 أحرف s1 و s2 و s3 و s4
ق 1 = 0 ؛ ق 2 = 00 ؛ ق 3 = 01 ؛ ق 4 = 11.كيف يجب على المتلقي تفسير التعبير المستلم التالي
0011 ؟
كيف
s1s1s4 أو كيف
s2s4 ؟
لا يمكنك إعطاء إجابة لا لبس فيها على هذا السؤال ، فمن المؤكد أنه لم يتم فك شفرة هذا الرمز ، وبالتالي فهو غير مرضٍ. كود ، من ناحية أخرى
ق 1 = 0 ؛ ق 2 = 10 ؛ ق 3 = 110 ؛ ق 4 = 111فك شفرة الرسالة بطريقة فريدة. خذ سلسلة عشوائية وفكر في كيفية فك المتلقي لها. تحتاج إلى بناء شجرة فك شفرة وفقًا للشكل في الشكل 10.II. سلسلة
1101000010011011100010100110 ...
يمكن تقسيمها إلى كتل من الأحرف
110 ، 10 ، 0 ، 10 ، 0 ، 110 ، 111 ، 0 ، 0 ، 0 ، 10 ، 10 ، 0 ، 110 ، ...
وفقًا للقاعدة التالية لبناء شجرة فك التشفير:
إذا كنت في أعلى الشجرة ، فاقرأ الحرف التالي. عندما تصل إلى ورقة شجرة ، تقوم بتحويل التسلسل إلى حرف والعودة إلى البداية.
سبب وجود مثل هذه الشجرة هو أنه لا يوجد حرف هو بادئة للآخر ، لذا فأنت تعرف دائمًا متى تحتاج إلى العودة إلى بداية شجرة فك التشفير.
من الضروري الانتباه إلى ما يلي. أولاً ، يعد فك التشفير عملية دفق صارمة ، حيث يتم فحص كل بتة مرة واحدة فقط. ثانيًا ، تتضمن البروتوكولات عادةً أحرفًا تمثل علامة على نهاية عملية فك التشفير وهي ضرورية للإشارة إلى نهاية الرسالة.
يعد الفشل في استخدام حرف زائدة خطأ شائعًا في تصميم التعليمات البرمجية. بالطبع ، يمكنك توفير وضع فك تشفير ثابت ، وفي هذه الحالة لا تكون هناك حاجة إلى الحرف اللاحق.
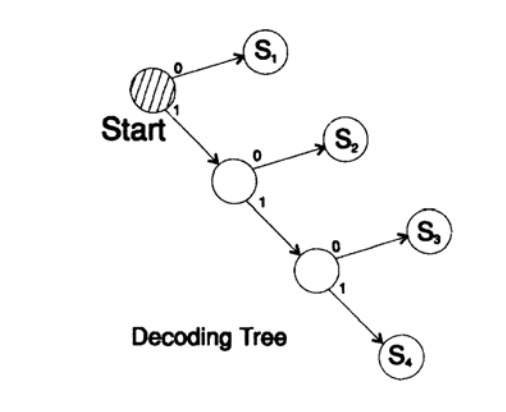الشكل 10.IIالسؤال التالي هو رموز لفك تشفير الدفق (الفوري). ضع في اعتبارك الرمز الذي تم الحصول عليه من الرمز السابق عن طريق عرض الأحرف
ق 1 = 0 ؛ ق 2 = 01 ؛ ق 3 = 011 ؛ ق 4 = 111.لنفترض أننا حصلنا على التسلسل
011111 ... 111 . الطريقة الوحيدة لفك نص الرسالة هي تجميع البتات من نهاية 3 إلى مجموعة وتحديد مجموعات بصفر بادئ أمامها ، وبعد ذلك يمكنك فك تشفيرها. يتم فك هذا الرمز بطريقة فريدة ، ولكن ليس على الفور! لفك الشفرة ، يجب أن تنتظر حتى نهاية التحويل! في الممارسة العملية ، يلغي هذا النهج معدل فك التشفير (نظرية ماكميلان) ، لذلك ، من الضروري البحث عن طرق فك التشفير الفوري.
فكر في طريقتين لترميز نفس الحرف Si:
ق 1 = 0 ؛ ق 2 = 10 ؛ ق 3 = 110 ؛ ق 4 = 1110 ، ق 5 = 1111 ،يوضح الشكل 10.III شجرة فك التشفير لهذه الطريقة.
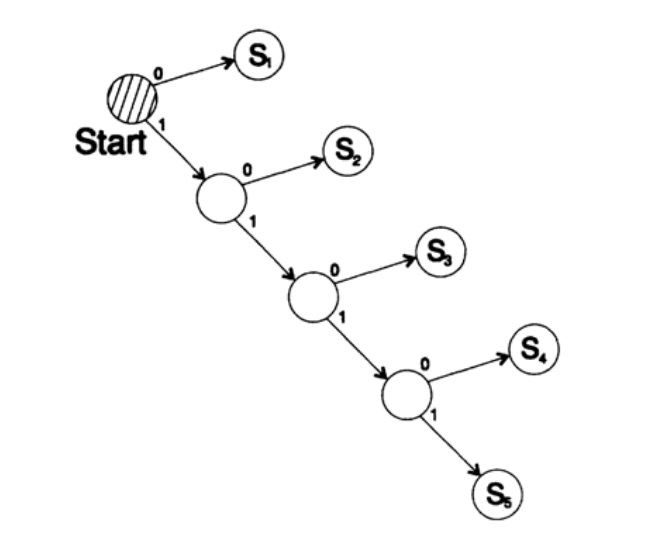الشكل 10.IIIالطريقة الثانية
ق 1 = 00 ؛ ق 2 = 01 ؛ ق 3 = 100 ؛ ق 4 = 110 ، ق 5 = 111 ،
يوضح الشكل 10.IV شجرة فك التشفير لهذه الرعاية.
الطريقة الأكثر وضوحًا لقياس جودة الشفرة هي متوسط طول مجموعة من الرسائل. لهذا ، من الضروري حساب طول الرمز لكل حرف مضروبًا في الاحتمال المقابل لحدوث pi. وبالتالي ، يتم الحصول على طول الرمز بأكمله. صيغة متوسط طول الرمز L لأحرف الأبجدية هي كالتالي
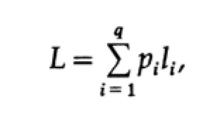
حيث pi هو احتمال حدوث الرمز si ، li هو الطول المقابل للرمز المشفر. للحصول على تعليمات برمجية فعالة ، يجب أن تكون قيمة L صغيرة قدر الإمكان. إذا كانت P1 = 1/2 و p2 = 1/4 و p3 = 1/8 و p4 = 1/16 و p5 = 1/16 ، فإننا نحصل على قيمة طول الكود في الكود # 1
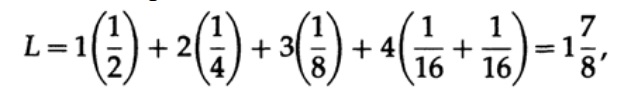
وللرمز # 2
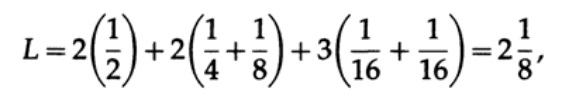
تشير القيم التي تم الحصول عليها إلى تفضيل الكود الأول.
إذا كانت جميع الكلمات في الأبجدية لها نفس احتمالية حدوثها ، فسيكون الرمز الثاني أكثر تفضيلاً. على سبيل المثال ، مع pi = 1/5 ، طول الرمز # 1
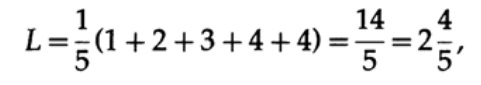
وطول الرمز # 2
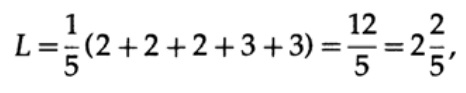
تظهر هذه النتيجة تفضيل لرمزين. وبالتالي ، عند تطوير كود "جيد" ، من الضروري النظر في احتمالية ظهور الأحرف.
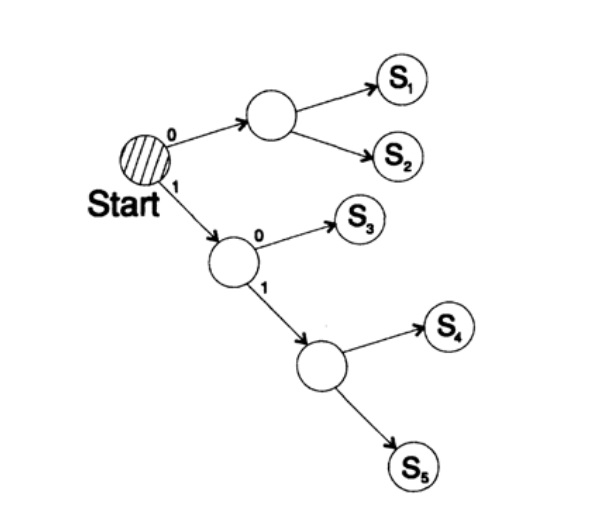الشكل 10.IV
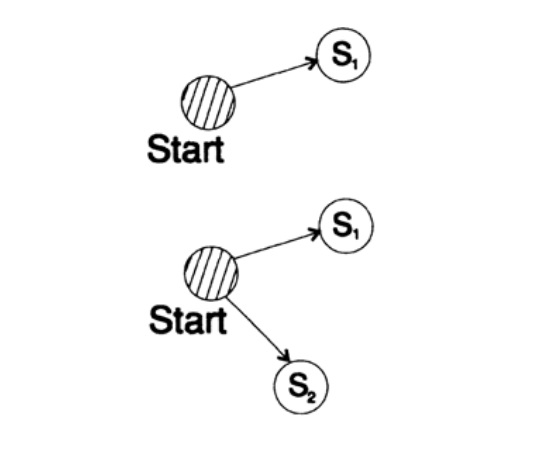الشكل 10.Vالنظر في عدم المساواة كرافت ، والتي تحدد القيمة الحدية لطول رمز الرمز li. في الأساس 2 ، يتم تمثيل عدم المساواة كما
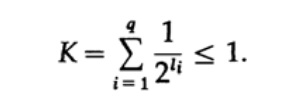
يشير عدم المساواة هذا إلى أن الأبجدية لا يمكن أن تحتوي على عدد كبير جدًا من الأحرف القصيرة ، وإلا سيكون المجموع كبيرًا جدًا.
لإثبات عدم المساواة في Kraft لأي كود فريد يتم فك شفرته ، نقوم ببناء شجرة فك التشفير ونطبق طريقة الاستقراء الرياضي. إذا كانت الشجرة تحتوي على ورقة أو ورقتين ، كما هو موضح في الشكل 10.V ، فلا شك في أن التفاوت صحيح. علاوة على ذلك ، إذا كانت الشجرة تحتوي على أكثر من ورقتين ، فإننا نقسم الشجرة الطويلة m إلى شجرتين فرعيتين. وفقًا لمبدأ الاستقراء ، نفترض أن التفاوت صحيح لكل فرع من ارتفاع m -1 أو أقل. وفقًا لمبدأ الاستقراء ، تطبيق اللامساواة على كل فرع. تشير إلى أطوال رموز الفرعين K 'و K'. عند الجمع بين فرعين لشجرة ، يزداد طول كل منهما بمقدار 1 ، وبالتالي ، يتكون طول الكود من مجموع K '/ 2 و K' '/ 2 ،
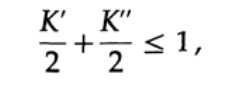
تم إثبات النظرية.
تأمل في إثبات نظرية ماكميلان. نحن نطبق عدم المساواة كرافت على رموز فك التشفير. يعتمد الدليل على حقيقة أنه بالنسبة لأي رقم K> 1 ، من الواضح أن القوة n للرقم هي أكثر من دالة خطية لـ n ، حيث n عدد كبير إلى حد ما. نرفع عدم المساواة كرافت إلى القوة nth وتقديم التعبير كمجموع
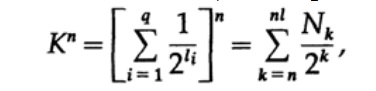
حيث Nk هو عدد أحرف الطول k ، يبدأ التلخيص بالحد الأدنى لطول التمثيل n للحرف وينتهي بالحد الأقصى للطول nl ، حيث l هو الحد الأقصى لطول الحرف المشفر. من شرط فك التشفير الفريد يتبع ذلك. يتم تقديم المبلغ على النحو
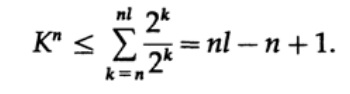
إذا كانت K> 1 ، فمن الضروري إنشاء n كبيرة بما يكفي لتصبح التفاوت كاذبة. لذلك ، ك <= 1 ؛ ثبتت نظرية ماكميلان.
تأمل بعض الأمثلة على تطبيق عدم المساواة كرافت. هل يمكن أن يوجد رمز فريد مشفر بأطوال 1 ، 3 ، 3 ، 3؟ نعم منذ ذلك الحين
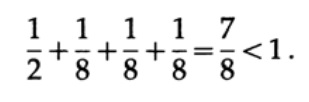
ماذا عن أطوال 1 ، 2 ، 2 ، 3؟ احسب وفقا للصيغة
انتهكت عدم المساواة! هناك عدد كبير جدًا من الأحرف القصيرة في هذا الرمز.
رموز الفاصلة هي رموز تتكون من أحرف 1 ، وتنتهي بحرف 0 ، باستثناء الحرف الأخير الذي يتكون من جميع الرموز. واحدة من الحالات الخاصة هي الرمز.
ق 1 = 0 ؛ ق 2 = 10 ؛ ق 3 = 110 ؛ ق 4 = 1110 ؛ ق 5 = 11111.للحصول على هذا الرمز ، نحصل على التعبير عن عدم المساواة Kraft
في هذه الحالة ، نحقق المساواة. من السهل أن نرى أنه بالنسبة لرموز النقاط ، يتحول عدم المساواة في كرافت إلى المساواة.
عند بناء رمز ، تحتاج إلى الانتباه إلى كمية كرافت. إذا بدأ مبلغ كرافت في تجاوز 1 ، فهذه إشارة حول الحاجة إلى تضمين حرف بطول مختلف لتقليل متوسط طول الرمز.
وتجدر الإشارة إلى أن عدم المساواة في Kraft لا يعني أن هذا الرمز غير قابل للفك بشكل فريد ، ولكن هناك رمز بأحرف من هذا الطول يتم فك تشفيره بشكل فريد. لإنشاء رمز فريد تم فك ترميزه ، يمكنك تعيين الطول المقابل بالبتات مع رقم ثنائي. على سبيل المثال ، للأطوال 2 ، 2 ، 3 ، 3 ، 4 ، 4 ، 4 ، 4 ، نحصل على عدم المساواة في كرافت
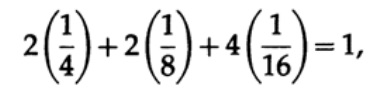
لذلك ، قد يوجد رمز دفق مشفر فريد.
ق 1 = 00 ؛ ق 2 = 01 ؛ ق 3 = 100 ؛ ق 4 = 101 ؛
ق 5 = 1100 ؛ ق 6 = 1101 ؛ ق 7 = 1110 ؛ ق 8 = 1111 ؛أريد الانتباه لما يحدث بالفعل عندما نتبادل الأفكار. على سبيل المثال ، في هذا الوقت أريد نقل الفكرة من رأسي إلى رأسك. أنطق بعض الكلمات التي من خلالها ، كما أعتقد ، يمكنك فهم (فهم) هذه الفكرة.
ولكن عندما تريد نقل هذه الفكرة إلى صديقك بعد قليل ، فمن شبه المؤكد أنك ستلفظ كلمات مختلفة تمامًا. في الواقع ، لا يتم تضمين المعنى أو المعنى ضمن أي كلمات محددة. لقد استخدمت بعض الكلمات ، ويمكنك استخدام كلمات مختلفة تمامًا لنقل نفس الفكرة. وبالتالي ، يمكن أن تنقل الكلمات المختلفة نفس المعلومات. ولكن بمجرد أن تخبر المحاور أنك لا تفهم الرسالة ، كقاعدة ، سيختار المحاور مجموعة مختلفة من الكلمات ، الثانية أو حتى الثالثة ، لنقل المعنى. وبالتالي ، لا يتم تضمين المعلومات في مجموعة من الكلمات المحددة. بمجرد تلقي هذه الكلمات أو تلك الكلمات ، فإنك تقوم بعمل كثير عند ترجمة الكلمات إلى فكرة يريد المحاور أن ينقلها إليك.
نتعلم اختيار الكلمات من أجل التكيف مع المحاور. بمعنى ما ، نختار كلمات تطابق أفكارنا ومستوى الضوضاء في القناة ، على الرغم من أن هذه المقارنة لا تعكس بدقة النموذج الذي أستخدمه لتمثيل الضوضاء في عملية فك التشفير. في المؤسسات الكبيرة ، تتمثل المشكلة الخطيرة في عدم قدرة المحاور على سماع ما قاله شخص آخر. في المناصب العليا ، يسمع الموظفون ما "يريدون سماعه". في بعض الحالات ، عليك أن تتذكر هذا عندما تصعد السلم الوظيفي. إن تقديم المعلومات في شكل رسمي هو انعكاس جزئي للعمليات من حياتنا وقد وجد تطبيقًا واسعًا يتجاوز حدود القواعد الرسمية في تطبيقات الكمبيوتر.
يتبع ...من يريد المساعدة في ترجمة الكتاب وتخطيطه ونشره - الكتابة في بريد إلكتروني شخصي أو بريد magisterludi2016@yandex.ruبالمناسبة ، أطلقنا أيضًا ترجمة كتاب رائع آخر -
"آلة الأحلام: تاريخ ثورة الكمبيوتر" )