ضغط صفائف كبيرة من الأعداد الأولية

نادرًا ما تسمح لك خصائص الأعداد الأولية بالعمل معها بشكل مختلف عن شكل مصفوفة محسوبة مسبقًا - ويفضل أن تكون ضخمة قدر الإمكان. يعاني تنسيق التخزين الطبيعي في شكل أعداد صحيحة من سعة رقم أو آخر في نفس الوقت من بعض العيوب التي تصبح مهمة مع نمو حجم البيانات.

لذا ، فإن تنسيق الأعداد الصحيحة غير الموقعة ذات 16 بت بحجم مثل هذا الجدول يبلغ حوالي 13 كيلوبايت ، فهو يحتوي على 6542 وحدة فقط أساسية: متبوعًا بالرقم 65531 هي قيم عمق البتات الأعلى. هذه الطاولة مناسبة فقط كلعبة.

يبدو الشكل الصحيح الأكثر شيوعًا 32 بت في البرمجة أكثر صلابة - فهو يسمح لك بتخزين حوالي 203 مليون تنسيق بسيط. لكن مثل هذا الجدول يشغل بالفعل حوالي 775 ميغابايت.

تنسيق 64 بت له آفاق أكثر. ومع ذلك ، مع القوة النظرية لترتيب قيم 1e + 19 ، سيكون للجدول حجم 64 إكسابايت.

لا يعتقد حقًا أن إنسانيتنا التقدمية ستحسب في المستقبل المنظور جدولًا للأعداد الأولية لمثل هذا الحجم. والنقطة هنا ليست كثيرة في الأحجام حتى في وقت العد من الخوارزميات المتاحة. لنفترض أنه إذا كان لا يزال من الممكن حساب جدول كل 32 بت البسيطة بشكل مستقل في غضون ساعات قليلة (الشكل 1) ، فعندئذٍ بالنسبة للجدول على الأقل ، فإن الأمر بحجم أكبر سيستغرق عدة أيام. لكن مثل هذه الأحجام اليوم - هذا هو المستوى الأولي فقط.

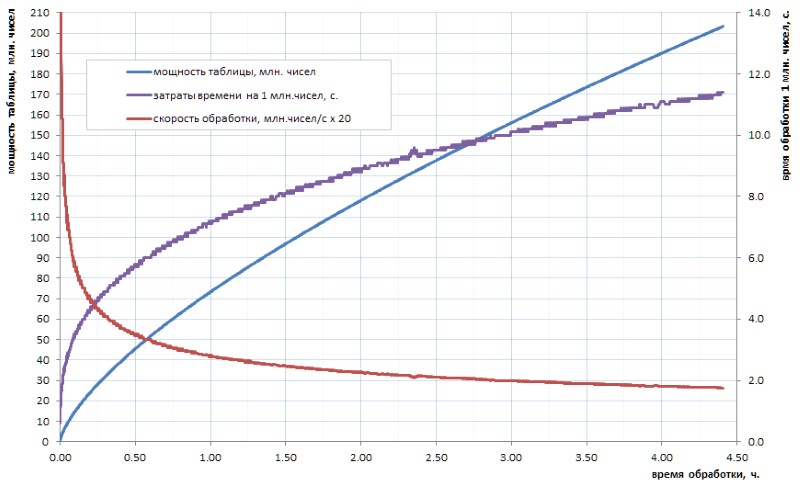
كما يمكن رؤيته من الرسم البياني ، فإن وقت الحساب المحدد بعد رعشة البداية يمر بسلاسة في النمو المقارب. إنه بطيء إلى حد ما. لكن هذا هو النمو ، مما يعني أن استخراج كل قطعة من البيانات التالية بمرور الوقت سيكون أكثر صعوبة. إذا كنت ترغب في تحقيق بعض الاختراق الهام ، فسيتعين عليك موازنة العمل عبر النوى (وهي موازية بشكل جيد) وتعليقها على أجهزة الكمبيوتر العملاقة. مع احتمال الحصول على أول 10 مليارات بسيط في الأسبوع ، و 100 مليار - فقط في السنة. بالطبع ، هناك خوارزميات أسرع لحساب بسيط من التمثال التافه المستخدم في واجبي المنزلي ، ولكن ، في جوهره ، هذا لا يغير الأمر: بعد أمرين أو ثلاثة من الحجم ، يصبح الوضع مشابهًا.

لذلك ، سيكون من الجميل أن تقوم بعمل العد مرة واحدة ، لتخزين نتائجه في شكل جدولي جاهز ، واستخدامها حسب الحاجة.

بسبب وضوح الفكرة ، تأتي الشبكة عبر العديد من الروابط إلى قوائم جاهزة من الأعداد الأولية التي تم حسابها بالفعل من قبل شخص ما. للأسف ، في معظم الحالات ، تكون مناسبة فقط للحرف اليدوية الطلابية: واحدة منها ، على سبيل المثال ، تتجول من موقع إلى آخر وتتضمن 50 مليون حرف بسيط. يمكن لهذا المبلغ فقط أن يذهل غير المبتدئين: فقد سبق ذكره أعلاه أنه على جهاز كمبيوتر منزلي في غضون ساعات قليلة يمكنك حساب جدول كل 32 بت البسيطة بشكل مستقل ، وهو أكبر بأربع مرات. ربما قبل حوالي 15 إلى 20 عامًا ، كانت هذه القائمة بالفعل إنجازًا بطوليًا للمجتمع العادي. اليوم ، في عصر الأجهزة متعددة النواة متعددة الجيجاهرتز وجيجابايت ، لم يعد هذا مثيرًا للإعجاب.

لقد كنت محظوظًا للتعرف على الوصول إلى جدول أكثر تمثيلًا من الجداول البسيطة ، والذي سأستخدمه أيضًا كتوضيح وتضحية لتجاربي الميدانية. لغرض التآمر ، سأتصل بها 1TPrimo . أنه يحتوي على جميع الأعداد الأولية أقل من تريليون.

باستخدام 1TPrimo كمثال ، من السهل معرفة الأحجام التي عليك التعامل معها. بسعة تبلغ حوالي 37.6 مليار قيمة بتنسيق صحيح 64 بت ، تبلغ هذه القائمة 280 غيغابايت. بالمناسبة - ذلك الجزء الذي يمكن أن يتسع لـ 32 رقمًا يمثل 0.5 ٪ فقط من عدد الأرقام الممثلة فيه. هذا يجعل من الواضح تمامًا أن أي عمل جاد مع الأعداد الأولية يميل حتمًا إلى إجمالي عمق البت 64 بت (أو أكثر).

وبالتالي ، فإن الاتجاه الكئيب واضح: إن جدول الأعداد الأولية الجاد بطريقة ما لديه حتما حجم ضخم. ويجب علينا محاربة هذا بطريقة أو بأخرى.

أول ما يتبادر إلى الذهن عند النظر إلى جدول (الشكل 2) هو أنه يتكون من قيم متتالية متطابقة تقريبًا تختلف فقط في واحد أو اثنين من الخانات العشرية الأخيرة:

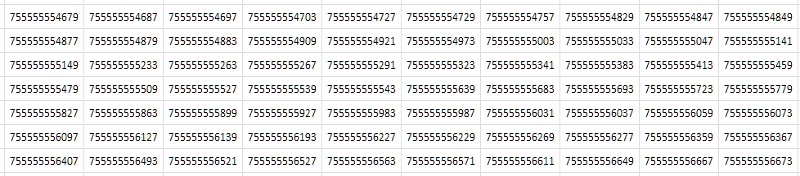
ببساطة ، من أكثر الاعتبارات العامة شيوعًا: إذا كان الملف يحتوي على الكثير من البيانات المكررة ، فيجب ضغطه جيدًا من قبل الأرشيف. في الواقع ، ضغط الجدول 1TPrimo باستخدام الأداة المساعدة 7-zip الشائعة في الإعدادات القياسية أعطى نسبة ضغط عالية إلى حد ما: 8.5. صحيح أن وقت المعالجة - مع الحجم الضخم للجدول المصدر - على خادم 8 نواة ، بمتوسط ​​تحميل لجميع النوى من حوالي 80-90٪ ، كان 14 ساعة و 12 دقيقة. تم تصميم خوارزميات الضغط العامة لبعض الأفكار المجردة والمعممة حول البيانات. في بعض الحالات الخاصة ، يمكن لخوارزميات الضغط المتخصصة المبنية على الميزات المعروفة جيدًا لمجموعة البيانات الواردة أن توضح مؤشرات أكثر فعالية ، والتي تم تخصيص هذا العمل لها. ومدى فعاليتها سوف تصبح واضحة أدناه.

تطلب القيم العددية القريبة من الأعداد الأولية المجاورة قرارًا بعدم تخزين هذه القيم نفسها ، ولكن الفواصل (الاختلافات) بينها. في هذه الحالة ، يمكن تحقيق وفورات كبيرة بسبب حقيقة أن عمق البتات للفترات الزمنية أقل بكثير من عمق البتات للبيانات الأولية (الشكل 3).

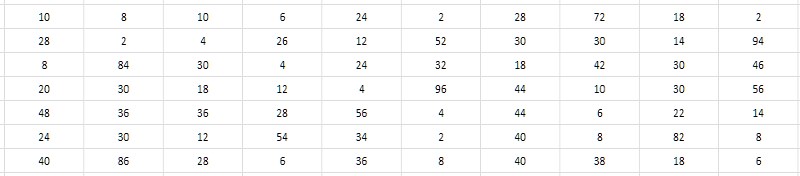
ويبدو أنه لا يعتمد على عمق البتات البسيطة التي تولد الفاصل الزمني. يُظهر البحث الشامل أن القيم النموذجية للفواصل الزمنية للأعداد الأولية المأخوذة من أماكن مختلفة في جدول 1TPrimo تقع داخل الوحدات ، والعشرات ، وأحيانًا المئات ، وربما - باعتبارها أول جملة عمل - يمكن أن تتناسب مع نطاق 8 بت الأعداد الصحيحة غير الموقعة ، أي وحدات البايت. سيكون الأمر مناسبًا للغاية ، وبالمقارنة مع تنسيق 64 بت ، سيؤدي هذا على الفور إلى ضغط البيانات 8 أضعاف - فقط في مكان ما على المستوى الذي يوضحه أرشيف 7-zip. علاوة على ذلك ، يجب أن يكون لبساطة خوارزميات الضغط وإلغاء الضغط من حيث المبدأ تأثير كبير على سرعة الضغط والوصول إلى البيانات مقارنة بـ 7-zip. يبدو مغريا.

من الواضح تمامًا أن البيانات التي تم تحويلها من قيمها المطلقة إلى الفواصل الزمنية النسبية بينها مناسبة فقط لاستعادة سلسلة من القيم الواردة في صف من بداية الجدول الأساسي. ولكن إذا أضفنا الحد الأدنى من بنية فهرس الكتلة إلى مثل هذا الجدول من الفواصل الزمنية ، فإن التكاليف الإضافية الإضافية غير المهمة ستسمح لنا باستعادة - ولكن بالفعل الكتلة حسب الكتلة - كل من عنصر الجدول برقمه وأقرب عنصر بقيمة محددة بشكل تعسفي ، وهذه العمليات ، جنبًا إلى جنب مع العملية الرئيسية عينات التسلسل - بشكل عام ، تستنفد حصة الأسد من الاستفسارات المحتملة لهذه البيانات. بالطبع ، ستصبح المعالجة الإحصائية أكثر تعقيدًا ، ولكنها ستظل شفافة تمامًا ، كما هو لا توجد حيلة معينة في استعادتها "بسرعة" من الفترات الزمنية المتاحة عند الوصول إلى كتلة البيانات المطلوبة.

لكن للأسف. تُظهر تجربة رقمية بسيطة على بيانات 1TPrimo أنه بالفعل في نهاية العشرات الثالثة من ملايين (هذا أقل من مائة بالمائة من حجم 1TPrimo) - ثم في كل مكان آخر - تقع الفترات الفاصلة بين الأعداد الأولية المجاورة بانتظام خارج نطاق 0.255.

ومع ذلك ، تكشف تجربة عددية معقدة قليلاً أن نمو الحد الأقصى للفاصل الزمني بين الأعدادات المجاورة مع نمو الجدول نفسه بطيء جدًا جدًا - مما يعني أن الفكرة لا تزال جيدة بطريقة ما.

تشير النظرة الثانية الأكثر قربًا إلى جدول الفواصل الزمنية إلى أنه من الممكن تخزين ليس الفرق نفسه ، بل النصف. نظرًا لأن جميع الأعداد الأولية الأكبر من 2 تبدو غريبة على التوالي ، فمن الواضح أن اختلافاتها حتى. وبناءً على ذلك ، يمكن تقليل الفروق بمقدار 2 دون خسارة القيمة ؛ وللاكتمال ، يمكن للمرء أيضًا طرح واحد من الحاصل الذي تم الحصول عليه من أجل استخدام قيمة الصفر التي لم تتم المطالبة بها بخلاف ذلك (الشكل 4). سيطلق على هذا الحد من الفواصل في وقت لاحق متجانسة ، على عكس الشكل الأولي المفكك ، الذي يسهل اختراقه ، حيث تحولت جميع القيم الفردية والصفر إلى عدم المطالبة بها.

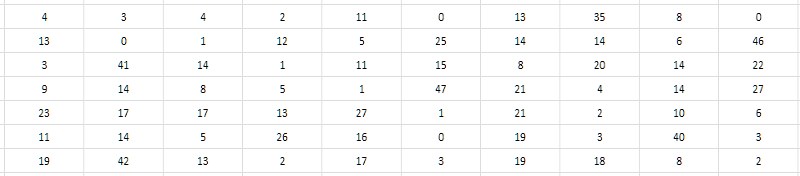
وتجدر الإشارة إلى أنه نظرًا لأن الفاصل الزمني بين الأولين البسيطين (2 و 3) لا يتناسب مع هذا المخطط ، فيجب استبعاد 2 من جدول الفترات الزمنية ووضع هذه الحقيقة في الاعتبار طوال الوقت.

تتيح لك هذه التقنية البسيطة ترميز الفواصل الزمنية من 2 إلى 512 في نطاق القيمة 0.255. ومرة ​​أخرى ، يأتي الأمل في أن طريقة الاختلاف ستسمح لنا بحزم تسلسل أكثر قوة من الأعدادات الأولية. وهو محق في ذلك: كشفت سلسلة قيمها 37.6 مليار المقدمة في قائمة 1TPrimo عن 6 فواصل زمنية (ستة!) ليست في النطاق 2..512.

لكن هذه كانت أخبار جيدة. الشيء السيئ هو أن هذه الفترات الستة متناثرة على القائمة بحرية تامة ، وأولها يحدث بالفعل في نهاية الثلث الأول من القائمة ، مما يجعل الثلثين المتبقيين على الصابورة غير مناسبين لطريقة الضغط هذه (الشكل 5):

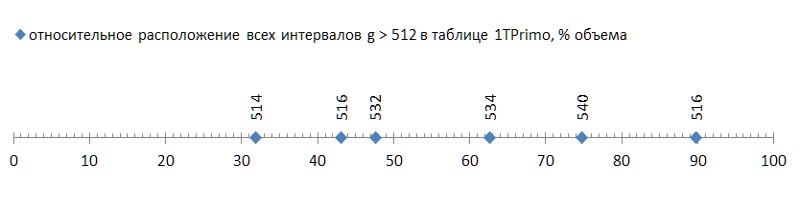
مثل هذا التدفق (بعض ست قطع مؤسفة لما يقرب من أربعين مليار! - وعليك ...) حتى مع ذبابة في المرهم للمقارنة - لإظهار شرف القطران. لكن للأسف ، هذا نمط وليس حادثًا. إذا قمنا بتتبع أول ظهور للفترات الفاصلة بين الأعداد الأولية اعتمادًا على طول البيانات ، يصبح من الواضح أن هذه الظاهرة تكمن في جينات الأعداد الأولية ، على الرغم من أنها تتقدم ببطء شديد (الشكل 6 *).

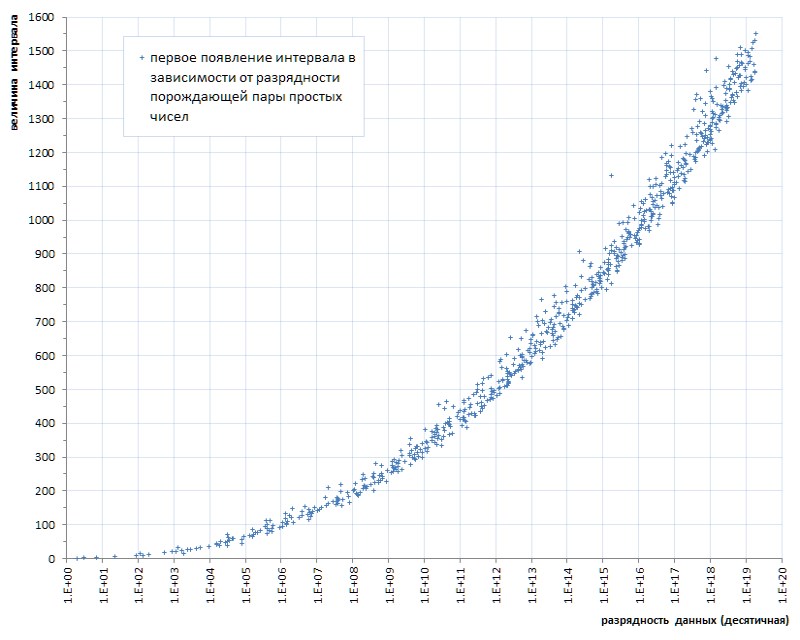
* جدول تم تجميعه وفقًا للموقع المواضيعي لتوماس ر. نيسلي ،
وهي عدة أوامر من حيث الحجم تفوق قوة قائمة 1TPrimo

ولكن حتى هذا التقدم البطيء جدًا يشير بشكل لا لبس فيه إلى أنه يمكن للمرء أن يقتصر على عمق بت معين محدد مسبقًا للفاصل الزمنية عند قوة معينة محددة مسبقًا من القائمة. أي أنها ليست مناسبة كحل عالمي.

ومع ذلك ، فإن حقيقة أن الطريقة المقترحة لضغط تسلسل من الأعداد الأولية تسمح لك بتنفيذ جدول مضغوط بسيط بسعة 12 مليار قيمة تقريبًا هي بالفعل نتيجة. يشغل هذا الجدول حجمًا قدره 11.1 غيغابايت - مقابل 89.4 غيغابايت بتنسيق 64 بت عادي. بالتأكيد بالنسبة لعدد من التطبيقات قد يكون هذا الحل كافياً.

وما هو مثير للاهتمام: إجراء ترجمة جدول 64 بت 1TPrimo إلى تنسيق فواصل 8 بت مع بنية كتلة ، باستخدام معالج واحد فقط (للتوازي ، سيكون عليك اللجوء إلى تعقيدات كبيرة في البرنامج ، ولم يكن الأمر يستحق ذلك على الإطلاق) ولا يزيد عن 5 ٪ من حمل المعالج (معظم الوقت الذي يقضيه في عمليات الملفات) استغرق 19 دقيقة فقط مقابل - أذكر - 14 ساعة على ثمانية نوى بنسبة 80-90٪ من الحمل الذي يقضيه أرشيف 7-zip.

بالطبع ، فقط الثلث الأول من الجدول تعرض لهذه الترجمة ، حيث لا يتجاوز نطاق الفواصل الزمنية 512. لذلك ، إذا جلبنا 14 ساعة كاملة إلى الثلث نفسه ، فيجب مقارنة 19 دقيقة مقابل 5 ساعات تقريبًا من 7-zip archiver. مع مقدار مماثل من الضغط (8 و 8.5) ، يكون الفرق حوالي 15 مرة. وبالنظر إلى أن نصيب الأسد من وقت عمل البرنامج الإذاعي كان مشغولاً بعمليات الملف ، فإن الفرق سيكون أكثر حدة على نظام قرص أسرع. وفكريًا ، يجب أن يحسب وقت تشغيل 7-zip على ثمانية نوى على خيط واحد ، وبعد ذلك ستصبح المقارنة كافية حقًا.

يختلف التحديد من قاعدة البيانات هذه قليلًا جدًا في الوقت عن التحديد من جدول البيانات غير المعبأة ويتم تحديده بالكامل تقريبًا حسب وقت عمليات الملف. تعتمد الأرقام المحددة بشدة على الأجهزة المحددة ، على الخادم الخاص بي ، في المتوسط ​​، استغرق الوصول إلى كتلة بيانات عشوائية 37.8 ميكرون ، بينما قراءة كتل متسلسلة - 4.2 ميكرون لكل كتلة ، لتفريغ الكتلة بالكامل - أقل من 1 ميكرون. أي أنه لا معنى لمقارنة ضغط البيانات مع عمل أرشيفي قياسي. وهذه إضافة كبيرة.

وأخيرًا ، تقدم الملاحظات حلًا ثالثًا آخر يزيل أي قيود على قوة البيانات: فترات التشفير بقيم ذات طول متغير. لطالما استخدمت هذه التقنية على نطاق واسع في التطبيقات المتعلقة بالضغط. معناه أنه إذا وجد في الإدخال أن بعض القيم يتم العثور عليها غالبًا ، وبعضها أقل شيوعًا ، وبعضها نادر جدًا ، فيمكننا ترميز الأول برموز قصيرة ، والثاني برموز أكثر أصالة ، والثالث - طويل جدًا (ربما طويل جدًا ، لأنه لا يهم: كل نفس ، هذه البيانات نادرة جدًا). ونتيجة لذلك ، يمكن أن يكون الطول الإجمالي للرموز المستلمة أقصر بكثير من بيانات الإدخال.

بالنظر بالفعل إلى الرسم البياني لمظهر الفترات في الشكل 7 ، يمكننا أن نفترض أنه إذا كانت الفترات هي 2 ، 4 ، 6 ، إلخ. تظهر في وقت أبكر من الفواصل الزمنية ، على سبيل المثال ، 100 ، 102 ، 104 ، وما إلى ذلك ، فيجب أن تستمر الأولى في الحدوث في كثير من الأحيان. والعكس بالعكس - إذا كانت الفواصل الزمنية 514 تأتي فقط بدءًا من 11.99 مليارًا ، و 516 - بدءًا من 16.2 مليارًا ، و 518 - بشكل عام بدءًا من 87.7 مليارًا فقط ، فستصادفهم نادرًا جدًا. بمعنى ، يمكننا أن نفترض مسبقًا العلاقة العكسية بين حجم الفاصل الزمني وتردده في سلسلة من الأعداد الأولية. وهذا يعني - يمكنك إنشاء بنية بسيطة تطبق رموزًا متغيرة الطول لهم.

بالطبع ، يجب أن تصبح الإحصائيات حول تواتر الفواصل الزمنية حاسمة لاختيار طريقة تشفير معينة. لحسن الحظ ، على عكس البيانات التعسفية ، فإن تواتر الفواصل بين الأعداد الأولية - التي هي في حد ذاتها تسلسل محدد بدقة ، مرة وإلى الأبد - هو أيضًا محدد بدقة ، مرة واحدة وإلى الأبد ، سمة محددة.

يوضح الشكل 7 استجابة التردد للفواصل الزمنية لقائمة 1TPrimo بأكملها:

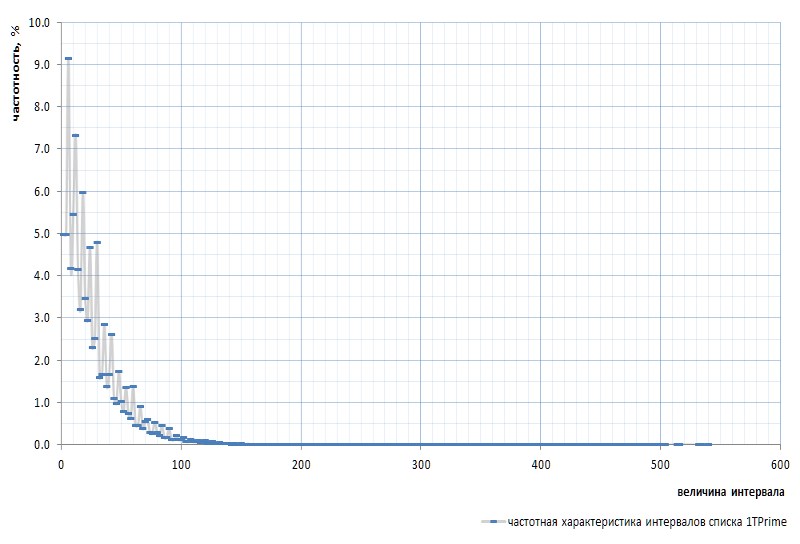
هنا من الضروري أن نذكر مرة أخرى أن الفترة الفاصلة بين الأعداد الأولية الأولى 2 و 3 مستثناة من الرسم البياني: هذا الفاصل الزمني 1 ويحدث مرة واحدة بالضبط في تسلسل الأعداد الأولية ، بغض النظر عن قوة القائمة. هذا الفاصل الزمني غريب للغاية بحيث أنه من الأسهل إزالة 2 من قائمة البسطاء بدلاً من الضلال باستمرار إلى التحفظات. تم التصريح عن أن الرقم 2 هو رقم افتراضي افتراضي : فهو غير مرئي في القوائم ، ولكنه موجود. مثل هذا غوفر.

للوهلة الأولى ، يؤكد الرسم البياني للتردد بشكل كامل الافتراض المسبق المقدم من فقرتين أعلاه. ويبين بوضوح عدم التجانس الإحصائي للفترات الزمنية وتكرار القيم الصغيرة مقارنةً بالقيم الكبيرة. ومع ذلك ، في العرض الثاني الأكثر تحديدًا ، يتبين أن الرسم البياني أكثر إثارة للاهتمام (الشكل 8):

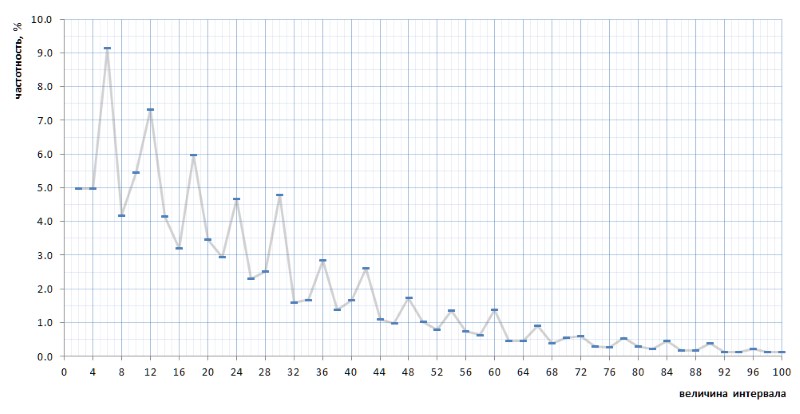
بشكل غير متوقع ، اتضح أن الفترات الأكثر تكرارًا ليست 2 و 4 ، كما يبدو أنها من اعتبارات عامة ، ولكن 6 و 12 و 18 ، تليها 10 - ثم 2 و 4 فقط بتردد متساوٍ تقريبًا (الفرق في 7 أرقام) بعد الفاصلة العشرية). علاوة على ذلك ، يتم تتبع تعدد قيم الذروة للرقم 6 عبر الرسم البياني بأكمله.

والأكثر إثارة للاهتمام أن هذه الطبيعة التي تم الكشف عنها عن غير قصد من الرسم البياني عالمية - وفي جميع التفاصيل ، مع جميع أوجه الخلل - عبر التسلسل الكامل للفواصل الزمنية البسيطة التي تمثلها قائمة 1TPrimo ، فمن المحتمل أنها عالمية لأي تسلسل من الفواصل الزمنية البسيطة (بالطبع ، مثل هذا البيان الجريء يحتاج إلى إثبات ، والذي يسرني جدًا نقله إلى أكتاف المتخصصين في نظرية الأعداد). يوضح الشكل 10 مقارنة إحصائيات الفاصل الكامل (الخط القرمزي) مع عينات فاصلة محدودة مأخوذة في عدة أماكن عشوائية في قائمة 1TPrimo (خطوط ألوان أخرى):

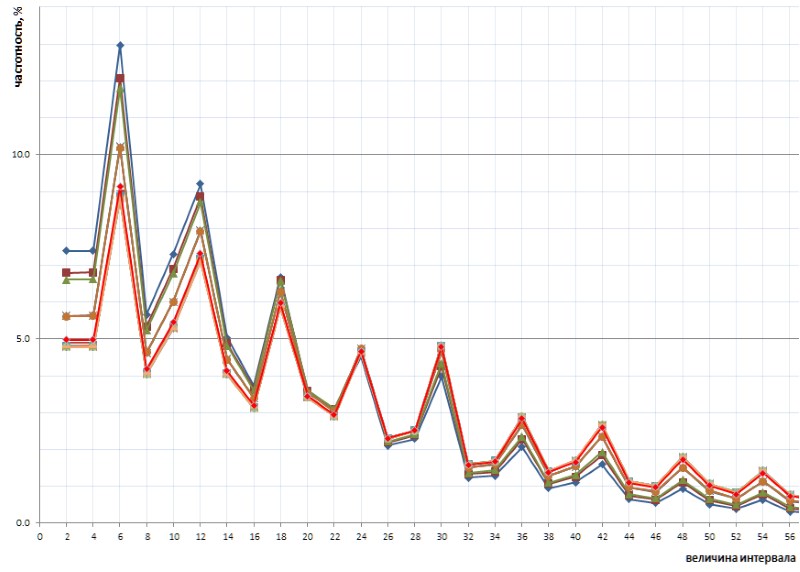
يمكن أن نرى من هذا الرسم البياني أن جميع هذه العينات تكرر بعضها البعض تمامًا ، مع وجود اختلاف طفيف فقط في الجزأين الأيسر والأيمن من الشكل: يبدو أنهما تم تدويرهما قليلاً عكس اتجاه عقارب الساعة حول نقطة الفاصل بقيمة 24. أجزاء من الرسومات مبنية على عينات ذات أعماق بت أقل. في مثل هذه العينات ، لا يوجد حتى الآن على الإطلاق ، أو الفترات الكبيرة نادرة ، والتي أصبحت متكررة في العينات ذات أعماق بت أعلى. وبناءً على ذلك ، فإن غيابهم لصالح تردد الفترات ذات القيم الدنيا. في العينات ذات أعماق بت أعلى ، تظهر العديد من الفواصل الزمنية الجديدة ذات القيم الكبيرة ؛ وبالتالي ، يقل تكرار الفترات الأصغر قليلاً. على الأرجح ، فإن النقطة المحورية ، مع زيادة قوة القائمة ، ستتحول نحو قيم أكبر. في مكان ما ، بجواره ، توجد نقطة التوازن للرسم البياني ، حيث يكون مجموع جميع القيم الموجودة على اليمين يساوي تقريبًا مجموع جميع القيم الموجودة على اليسار.

تقترح هذه الطبيعة المثيرة للاهتمام لتواتر الفواصل التخلي عن البنية التافهة لرموز ذات طول متغير. عادة ، يتكون هذا الهيكل من حزمة من القطع بأطوال وأغراض مختلفة. على سبيل المثال ، يأتي أولاً عدد معين من بتات البادئة التي تم تعيينها على قيمة معينة ، على سبيل المثال ، 0. هناك بت توقف خلفها ، والذي يجب أن يشير إلى اكتمال البادئة ، وبالتالي ، يجب أن يختلف عن البادئة: 1 في هذه الحالة. قد لا يكون للبادئة أي طول ، أي مرارًا وتكرارًا ، يمكن أن يبدأ أخذ العينات على الفور ببت توقف ، وبالتالي تحديد أقصر تسلسل. عادة ما يتبع بت الإيقاف لاحقة ، يتم تحديد طولها بطريقة محددة مسبقًا بطول البادئة. , , — . , - . - (, , - ) , .

, .

وهنا يجب ذكر شيء آخر مهم. للوهلة الأولى ، تشير الدورية التي تمت ملاحظتها إلى تقسيم الفترات إلى ثلاثيات: {2,4, 6 } ، {8,10, 12 } ، {14,16, 18 } وما إلى ذلك (يتم تمييز القيم ذات الحد الأقصى للتردد في كل ثلاثية بالخط العريض) . ومع ذلك ، في الواقع ، تختلف الدورة هنا قليلاً.

لن أذكر خط المنطق بأكمله ، الذي ، في الواقع ، غير موجود: كان تخمينًا بديهيًا ، مكملًا بطريقة تعداد صريح للخيارات والحسابات والعينات التي استغرقت عدة أيام متقطعة. النتيجة الدورية التي تم الكشف عنها تتكون من ستة فواصل زمنية {2,4, 6 ,8,10, 12 } و {14,16, 18 ,20,22, 24 } و {26,28, 30 ,32,34, 36 } و وما إلى ذلك (يتم تمييز فواصل التردد القصوى بالخط العريض مرة أخرى).

باختصار ، خوارزمية التعبئة المقترحة هي كما يلي.

يسمح لنا تقسيم الفواصل الزمنية إلى ستة أرقام زوجية بتمثيل أي فاصل زمني g بالصيغة g = i * 12 + t ، حيث i هو فهرس الستة التي ينتمي إليها هذا الفاصل ( i = {0,1,2,3, ...} ) و t هو ذيل يمثل إحدى القيم من مجموعة محددة ومحددة ومتطابقة بشكل صارم لأي ستة من المجموعة {2,4,6,8,10,12} . تتناسب استجابة التردد للمؤشر الموضح أعلاه بشكل عكسي تقريبًا مع قيمته ، لذلك فمن المنطقي تحويل الفهرس الستة إلى بنية تافهة لرمز متغير الطول ، ويرد مثال على ذلك أعلاه. تسمح لك خصائص تردد الكماشة بتقسيمه إلى مجموعتين يمكن ترميزهما بسلاسل بت ذات أطوال مختلفة: القيمتان 6 و 12 ، التي يتم العثور عليها في أغلب الأحيان ، يتم ترميزها بتة واحدة ، والقيم 2 و 4 و 8 و 10 ، التي يتم مواجهتها بشكل أقل تكرارًا ، يتم تشفيرها بتتين. بالطبع ، هناك حاجة إلى بت واحد آخر للتمييز بين هذين الخيارين.

يتم استكمال مصفوفة تحتوي على حزم بت بحقول ثابتة تحدد قيم البدء للبيانات المقدمة في الكتلة ، والكميات الأخرى المطلوبة لاستعادة بسيطة أو تسلسلية بسيطة عشوائية من الفترات المخزنة في الكتلة.

بالإضافة إلى هيكل مؤشر الكتلة هذا ، فإن استخدام الرموز ذات الطول المتغير معقد بسبب التكاليف الإضافية مقارنة بفترات البتات الثابتة.

عند استخدام فواصل زمنية ذات حجم ثابت ، يعد تحديد الكتلة التي يتم فيها البحث عن رقم أولي برقمه التسلسلي مهمة بسيطة إلى حد ما ، لأن عدد الفواصل الزمنية لكل كتلة معروف مسبقًا. لكن البحث عن حل بسيط لأقرب قيمة ليس له حل مباشر. بدلاً من ذلك ، يمكنك استخدام بعض الصيغة التجريبية التي تسمح لك بالعثور على رقم الكتلة التقريبي مع الفاصل الزمني المطلوب ، وبعد ذلك سيكون عليك البحث عن الكتلة المطلوبة عن طريق البحث الشامل.

بالنسبة للجدول الذي يحتوي على أكواد متغيرة الطول ، يلزم اتباع نفس النهج لكلا المهمتين: سواء لجلب قيمة حسب الرقم أو للبحث حسب القيمة. نظرًا لأن طول الرموز يختلف ، فلا يُعرف أبدًا مسبقًا عدد الاختلافات المخزنة في أي كتلة معينة ، وفي أي كتلة تكمن القيمة المطلوبة. تم تحديده تجريبيًا أنه مع حجم كتلة يبلغ 512 بايت (والذي يتضمن بعض وحدات بايت الرأس) ، يمكن أن تصل سعة الكتلة إلى 10-12 في المائة من متوسط ​​القيمة. تعطي الكتل الأصغر مبعثرًا نسبيًا أكبر. في الوقت نفسه ، يميل متوسط ​​قيمة سعة الكتلة نفسها إلى الانخفاض ببطء مع نمو الجدول. إن اختيار الصيغ التجريبية لتحديد غير دقيق للكتلة الأولية للبحث عن القيمة المطلوبة من حيث العدد والقيمة هي مهمة غير تافهة. بدلاً من ذلك ، يمكنك استخدام فهرسة أكثر تعقيدًا وتعقيدًا.

هذا ، في الواقع ، كل شيء.

أدناه ، يتم وصف التفاصيل الدقيقة لضغط جدول أولي باستخدام رموز متغيرة الطول والهياكل المرتبطة به بطرق أكثر رسمية وتفصيلًا ، ويتم إعطاء رمز وظائف فترات التعبئة والتفريغ في C.

النتيجة.

كمية البيانات المترجمة من الجدول 1TPrimo إلى أكواد متغيرة الطول ، تكملها بنية مؤشر كتلة ، كما هو موضح أدناه ، بلغت 26309،295،104 بايت (24.5 جيجابايت) ، أي أن نسبة الضغط تصل إلى 11.4. من الواضح أنه مع زيادة عمق البت ، ستزداد نسبة الضغط.

كان وقت البث 280 جيجا بايت من جدول 1TPrimo بالتنسيق الجديد 1 ساعة. هذه هي النتيجة المتوقعة بعد التجارب مع فترات التعبئة في أعداد صحيحة أحادية البايت. في كلتا الحالتين ، تتكون ترجمة الجدول المصدر بشكل رئيسي من عمليات الملف ولا تكاد تحمّل المعالج (في الحالة الثانية ، لا يزال الحمل أعلى بسبب التعقيد الحسابي العالي للخوارزمية). لا يختلف أيضًا وقت الوصول إلى البيانات كثيرًا عن الفواصل الزمنية البايتة الواحدة ، ولكن الوقت الذي يستغرقه فك كتلة كاملة من نفس الحجم استغرق 1.5 ميكرومتر ، بسبب التعقيد العالي للخوارزمية لاستخراج رموز متغيرة الطول.

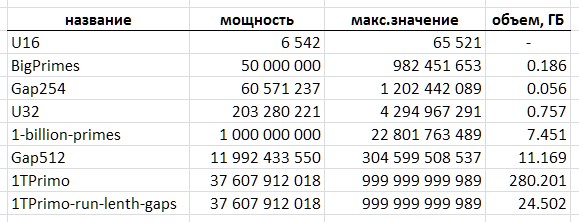
يلخص الجدول (الشكل 10) الخصائص الحجمية لجداول الأعداد الأولية المذكورة في هذا النص.

وصف خوارزمية الضغط

الشروط والتدوين

P (prime): P1=3, P2=5, P3=7 ... Pn, Pn1 هي الأعداد الأولية وفقًا P (prime): P1=3, P2=5, P3=7 ... Pn, Pn1 التسلسلية. مرة أخرى (وللمرة الأخيرة) أؤكد أن P0=2 هو رقم أولي افتراضي ؛ من أجل التوحيد الرسمي ، يتم استبعاد هذا الرقم ماديًا من قائمة الأعداد الأولية.

G (gap) - الفاصل الزمني بين جهتين متتاليتين Gn = Pn1 - Pn; G={2,4,6,8 ...} Gn = Pn1 - Pn; G={2,4,6,8 ...} .

D (dense) - يتم تقليله إلى فاصل زمني متآلف: D = G/2 -1; D={0,1,2,3 ...} D = G/2 -1; D={0,1,2,3 ...} . تبدو الفترات الستة في الشكل {0,1,2,3,4,5}, {6,7,8,9,10,11}, {12,13,14,15,16,17} مثل {0,1,2,3,4,5}, {6,7,8,9,10,11}, {12,13,14,15,16,17} الخ.

Q (quotient) - اختزال مؤشر الستة إلى شكل أحادي ، Q = D div 6; Q={0,1,2,3 ...} Q = D div 6; Q={0,1,2,3 ...}

R (remainder) - ما تبقى من ستة متجانسة R = D mod 6. R لها دائمًا قيمة في النطاق {0,1,2,3,4,5} .

تخضع قيم Q و R التي يتم الحصول عليها بواسطة الطريقة المذكورة أعلاه من أي فاصل تعسفي G ، نظرًا لخصائص ترددها المستقرة ، للضغط والتخزين في شكل حزم بتات متغيرة الطول ، موصوفة أدناه. يتم إنشاء سلاسل البتات التي ترميز قيم Q و R في حزمة بطرق مختلفة: لتشفير مؤشر Q ، يتم استخدام سلسلة البتات للبادئة H والتدفق F والبتة المساعدة S مجموعة البتات من infix X والبتة المساعدة A لترميز الباقي R

A (arbiter) - بت يحدد حجم infix X : 0 - بت واحد بت ، 1 - بتان.

X (infix) - 1 أو 2-bit infix ، مع البت الحكمي ، يحددان قيمة R بشكل تبادلي (يوضح الجدول أيضًا تكرار الستة الأولى بمثل هذه الدلائل كمرجع):

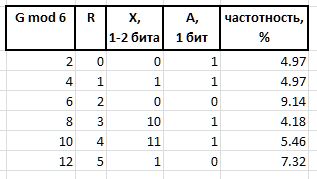
F (fluxion) هو تدفق ، مشتق من المؤشر Q بطول متغير L={0,1,2...} ، مصمم للتمييز بين دلالات سلاسل البت (), 0, 00, 000, أو 1, 01, 001 ، إلخ. د.

يتم التعبير عن سلسلة بت من وحدات الطول L كـ 2^L - 1 (العلامة ^ تعني الأسي). في تدوين C ، يمكن الحصول على نفس القيمة من خلال التعبير 1<<L - 1 . ثم يمكن الحصول على قيمة fluxia ذات الطول L من Q التعبير

 F = Q - (1 << L - 1) ،

واستعادة Q من فلوكسيا عن طريق التعبير

 س = (1 << L - 1) + F.

كمثال ، للكميات Q = {0..15} ، سيتم الحصول على سلاسل بتات التدفق:

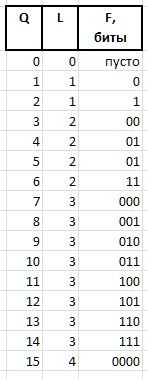
آخر حقلين بتين ضروريين لقيم التعبئة / الاستعادة هي:

H (header) - البادئة ، سلسلة من البتات مضبوطة على 0.

S (stop) - بت الإيقاف مضبوط على 1 ، منتهيًا البادئة.

في الواقع ، تتم معالجة هذه البتات أولاً في سلاسل بت ، فهي تسمح لك بتحديد أثناء التفريغ أو تعيين أثناء التعبئة حجم التدفق وبداية الحكم وحقول التدفق - مباشرة بعد بت التوقف.

W (width) - عرض الكود بالكامل بالبتات.

ويبين الشكل 11 البنية الكاملة لرزمة البتات:

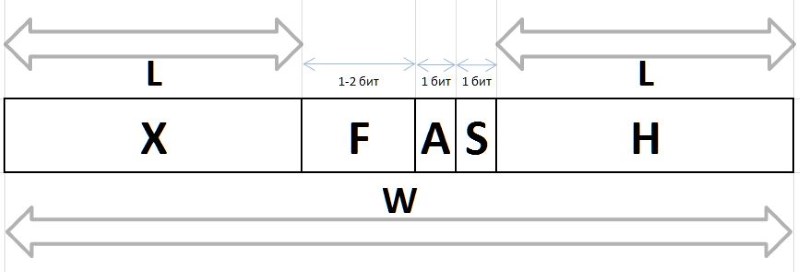
تسمح لنا قيم Q و R المستردة من هذه السلاسل باستعادة القيمة الأولية للفاصل الزمني:

 D = Q * 6 + R ،
 G = (D + 1) * 2 ،

ويسمح لك تسلسل الفواصل الزمنية المستعادة باستعادة الأعداد الأولية الأصلية من قيمة أساسية معينة للكتلة (كتلة بذور الفواصل الزمنية) عن طريق إضافة جميع الفواصل الزمنية لهذه الكتلة بالتسلسل.

للعمل مع سلاسل البت ، يتم استخدام متغير صحيح 32 بت ، حيث تتم معالجة البتات الأقل أهمية وبعد استخدامها ، يتم تحويل البتات إلى اليسار عند التعبئة أو إلى اليمين عند التفريغ.

هيكل الكتلة

بالإضافة إلى سلاسل البت ، تحتوي الكتلة على المعلومات اللازمة لجلب أو إضافة البتات ، وكذلك لتحديد محتويات الكتلة.

 //      //    typedef unsigned char BYTE; typedef unsigned short WORD; typedef unsigned int LONG; typedef unsigned long long HUGE; typedef int BOOL; #define TRUE 1 #define FALSE 0 #define BLOCKSIZE (256) // :   , #define HEADSIZE (8+8+2+2+2) //   , #define BODYSIZE (BLOCKSIZE-HEADSIZE) //   . //           typedef struct { HUGE base; //  ,      HUGE card; //        WORD count; //      WORD delta; // base+delta =      WORD offset; //        BYTE body[BODYSIZE]; //    } crunch_block; //    ,   put()  get() crunch_block block; //       . // NB:  len/val  rev/rel     //  ,    ,   //    . static struct tail_t { BYTE len; //      S  A BYTE val; //  ,   A  - S BYTE rev; //    BYTE rel; //    } tails[6] = { { 4, 3, 2, 3 }, { 4, 7, 5, 3 }, { 3, 1, 0, 4 }, { 4,11, 1, 4 }, { 4,15, 3, 4 }, { 3, 5, 4, 4 } }; //             BOOL put(int gap) { // 1.      int Q, R, L; //   (),  (),   int val = gap / 2 - 1; Q = val / 6; R = val % 6; L = -1; // .., 0 - 1 val = Q + 1; while (val) { val >>= 1; L++; } //    L val = Q - (1 << L) + 1; //  val <<= tails[R].len; val += tails[R].val; //      val <<= L; //   L += L + tails[R].len; //    // 2.   val  L   buffer   put_index if (block.offset + L > BODYSIZE * 8) // !      return FALSE; Q = (block.offset / 8); //  ,      R = block.offset % 8; //     block.offset += L; //      block.count++; //     block.delta += gap; if (R > 0) //        { val <<= R; val |= block.body[Q]; L += R; } //     L = L / 8 + ((L % 8) > 0 ? 1 : 0); //     while (L-- > 0) { block.body[Q++] = (char)val; val >>= 8; } return TRUE; } //          int get_index; //         //      int get() { if (get_index >= BODYSIZE * 8) return 0; //      int val = *((int*)&block.body[get_index / 8]) >> get_index % 8; //  4   if (val == 0) return -1; // !       int Q, R, L, F, M, len; // , , , ,     L = 0; while (!(val & 1)) { val >>= 1; L++; } //  -     if ((val & 3) == 1) //       R = (val >> 2) & 1; //   else R = ((val >> 2) & 3) + 2; //   len = tails[R].rel; get_index += 2 * L + len; val >>= len; M = ((1 << L) - 1); //   F = val & M; //    Q = F + M; //   return 2 * (1 + (6 * Q + tails[R].rev)); //         } 

التحسينات

إذا قمنا بتغذية قاعدة الفواصل التي تم الحصول عليها لنفس أرشيف 7-zip ، ففي ساعة ونصف من العمل المكثف على خادم 8 نواة ، فإنه يتمكن من ضغط ملف الإدخال بنسبة 5٪ تقريبًا. أي أنه في قاعدة بيانات الفترات ذات الطول المتغير من وجهة نظر الأرشيف ، لا يزال هناك بعض التكرار. لذلك هناك سبب للتكهن قليلاً (بالمعنى الجيد للكلمة) حول موضوع تقليل تكرار البيانات بشكل أكبر.

الحتمية الأساسية لتسلسل الفواصل بين الأعداد الأولية تجعل من الممكن إجراء حسابات دقيقة لكفاءة التشفير بطريقة أو بأخرى. على وجه الخصوص ، جعلت الرسومات الصغيرة (والفوضوية إلى حد ما) من الممكن استخلاص استنتاج أساسي حول مزايا ترميز الستات على ثلاث مرات ، وحول مزايا الطريقة المقترحة على الرموز التافهة ذات الطول المتغير (الشكل 12):

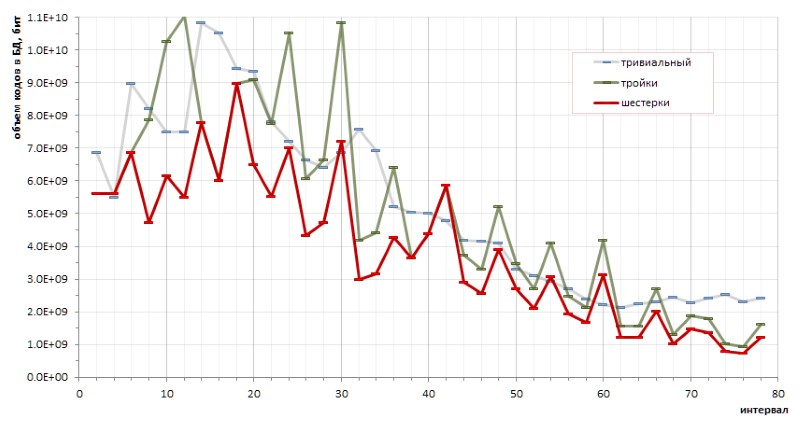
ومع ذلك ، تشير الارتفاعات المزعجة للرسم البياني الأحمر بشفافية إلى أنه قد تكون هناك طرق تشفير أخرى من شأنها أن تجعل الرسم البياني أكثر لطفًا.

يشير اتجاه آخر إلى التحقق من تكرار الفترات الزمنية المتتالية. من الاعتبارات العامة: نظرًا لأن الفواصل الزمنية 6 و 12 و 18 هي الأكثر شيوعًا في مجموعة من الأعداد الأولية ، فمن المرجح أن يتم العثور عليها في أزواج (أزواج) وثلاثية (ثلاثية) وما شابه ذلك من مجموعات الفواصل. إذا كانت إمكانية تكرار الدوبلكس (وربما حتى ثلاثة توائم ... حسنا ، فجأة!) تبين أنها ذات دلالة إحصائية في الكتلة الإجمالية للفواصل الزمنية ، فمن المنطقي أن تترجمها إلى بعض التعليمات البرمجية المنفصلة.

تكشف التجربة واسعة النطاق عن هيمنة معينة على الزوجي الفردي على الآخرين. ومع ذلك ، إذا كانت القيادة المطلقة متوقعة للزوج (6,6) - 1.37٪ من جميع الزوجي - فإن الفائزين الآخرين في هذا التصنيف أقل وضوحًا بكثير:

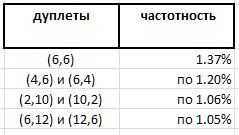
وبما أن الزوجي (6,6) متماثل ، وجميع الأزواج الأخرى المذكورة غير متماثلة ويتم العثور عليها في الترتيب بواسطة الزوجي المرآة بنفس التردد ، فيبدو أن السجل القياسي للمزدوج (6,6) في هذه السلسلة يجب تقسيمه إلى نصف بين الزوجي الذي لا يمكن تمييزه (6,6) و (6,6) ، مما يأخذهم 0.68٪ نزولاً إلى حد قائمة الجوائز. وهذا يؤكد مرة أخرى الملاحظة التي مفادها أنه لا يمكن إجراء التخمينات الحقيقية حول الأعداد الأولية دون مفاجآت.

كما توضح إحصائيات الثلاثيات قيادة مثل هذه الفترات الثلاثية ، والتي لا تتناسب تمامًا مع الافتراض المضاربي الناتج عن أعلى تردد للفترات 6 ، 12 ، 18. في تناقص ترتيب الشعبية ، يبدو قادة التردد بين الثلاثة توائم على النحو التالي:

الخ.

أخشى ، مع ذلك ، أن نتائج تكهناتي ستكون أقل أهمية للمبرمجين من اهتمام علماء الرياضيات ، ربما بسبب التصحيحات غير المتوقعة التي أجراها الممارسة في التخمينات البديهية. من غير المحتمل أن يكون من الممكن التخلص من أي أرباح كبيرة من النسبة المئوية المذكورة من التردد لصالح زيادة أخرى في نسبة الضغط ، في حين أن تعقيد الخوارزمية يهدد بالنمو بشكل كبير.

القيود

وقد لوحظ بالفعل أعلاه أن الزيادة في القيمة القصوى للفواصل فيما يتعلق بسعة الأعداد الأولية بطيئة جدًا جدًا. على وجه الخصوص ، يمكن أن نرى من الشكل 6 أن الفترة الفاصلة بين الأعداد الأولية التي يمكن تمثيلها بتنسيق عدد صحيح بدون إشارة 64 بت سيكون أقل من 1600.

يسمح لك التطبيق الموصوف بحزم وفك أي قيم فاصلة ذات 18 بت بشكل صحيح (في الواقع ، يحدث أول خطأ في التعبئة والتغليف بفاصل إدخال 442358). ليس لدي ما يكفي من الخيال لافتراض أن قاعدة بيانات الفواصل الزمنية يمكن أن تنمو إلى مثل هذه القيم: مرتدة في مكان ما حول عدد صحيح من 100 بت ، ولحساب الكسل بشكل أكثر دقة. في حالة الحريق ، لن يكون توسيع نطاق الفواصل الزمنية في بعض الأحيان صعبًا.

شكرا لقراءتك هذا المكان :)