مقدمة:
في النمذجة الرياضية لعدد من الأجهزة التقنية ، يتم استخدام أنظمة المعادلات التفاضلية غير الخطية. لا يتم استخدام هذه النماذج في التكنولوجيا فحسب ، بل يتم استخدامها في الاقتصاد والكيمياء والبيولوجيا والطب والإدارة.
تتطلب دراسة عمل هذه الأجهزة حل أنظمة المعادلات هذه. نظرًا لأن معظم هذه المعادلات غير خطية وغير ثابتة ، فمن المستحيل غالبًا الحصول على حلها التحليلي.
هناك حاجة لاستخدام الطرق العددية ، وأشهرها طريقة رونج - كوتا [1]. بالنسبة لـ Python ، في المنشورات حول الأساليب العددية ، على سبيل المثال [2،3] ، هناك القليل جدًا من البيانات حول استخدام Runge - Kutta ، ولا توجد بيانات حول تعديلها على طريقة Runge - Kutta - Felberg.
في الوقت الحالي ، وبفضل واجهته البسيطة ، فإن وظيفة odeint من وحدة scipy. Integrate لها أكبر توزيع في Python. تطبق الوظيفة الثانية من هذه الوحدة العديد من الطرق ، بما في ذلك طريقة رانج-كوتا-فيلبيرج الخمسة ذات الرتبة المذكورة ، ولكن ، بسبب عالميتها ، لديها أداء محدود.
الغرض من هذا المنشور هو تحليل مقارن للوسائل المذكورة لحل أنظمة المعادلات التفاضلية عدديًا مع مؤلف معدل تحت Python باستخدام طريقة Runge-Kutta-Felberg. يوفر المنشور أيضًا حلولًا لمشكلات القيمة الحدية لأنظمة المعادلات التفاضلية (SDEs).
موجز البيانات النظرية والفعلية حول الأساليب والبرامج المدروسة للحل العددي لل CDS
مشكلة كوشيبالنسبة لمعادلة تفاضلية واحدة من الترتيب التاسع ، تتكون مشكلة كوشي من إيجاد وظيفة تفي بالمساواة:
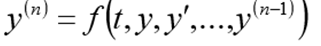
والظروف الأولية
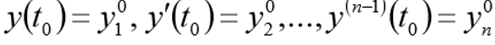
قبل حل هذه المشكلة يجب إعادة كتابتها في شكل CDS التالي
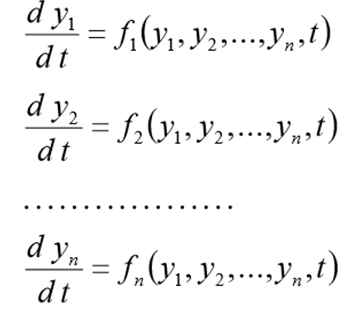
(1)
بشروط أولية
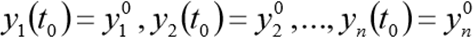 وحدة Scipy. دمج
وحدة Scipy. دمجتحتوي الوحدة على وظيفتين ode () و odeint () ، مصممة لحل أنظمة المعادلات التفاضلية العادية (ODEs) من الدرجة الأولى مع الشروط الأولية عند نقطة واحدة (مشكلة كوشي). تعد وظيفة ode () أكثر عمومية ، ووظيفة odeint () (مدمج ODE) لها واجهة أبسط وتحل معظم المشاكل بشكل جيد.
دالة Odeint ()تحتوي الدالة odeint () على ثلاث وسائط مطلوبة والعديد من الخيارات. يحتوي على التنسيق التالي odeint (func، y0، t [، args = ()، ...]) الوسيطة func هي اسم Python لوظيفة متغيرين ، أولهما قائمة y = [y1، y2، ...، yn ] ، والثاني هو اسم المتغير المستقل.
يجب أن تُرجع الدالة Func قائمة بقيم الدالة n
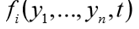
لقيمة معينة من حجة مستقلة ر. في الواقع ، تطبق الدالة func (y، t) حساب الجوانب اليمنى للنظام (1).
الوسيطة الثانية y0 لـ odeint () هي صفيف (أو قائمة) من القيم الأولية
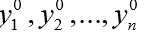
عند t = t0.
الوسيطة الثالثة هي مجموعة من النقاط الزمنية التي تريد فيها الحصول على حل للمشكلة. في هذه الحالة ، يعتبر العنصر الأول من هذا المصفوفة t0.
تعرض الدالة odeint () صفيفًا من الحجم len (t) x len (y0). تحتوي وظيفة odeint () على العديد من الخيارات التي تتحكم في تشغيلها. الخياران rtol (خطأ نسبي) و atol (خطأ مطلق) يحددان خطأ الحساب ei لكل قيمة من yi وفقًا للصيغة
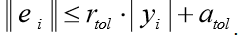
يمكن أن تكون ناقلات أو عددي. افتراضيًا
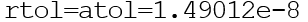 دالة Ode ()
دالة Ode ()الوظيفة الثانية للوحدة scipy.كامل ، المصممة لحل المعادلات والأنظمة التفاضلية ، تسمى ode (). يقوم بإنشاء كائن ODE (اكتب scipy. Integrate._ode.ode). وجود ارتباط لمثل هذا الشيء ، يجب على المرء استخدام أساليبه لحل المعادلات التفاضلية. على غرار وظيفة odeint () ، تتضمن وظيفة ode (func) اختزال المشكلة إلى نظام المعادلات التفاضلية للنموذج (1) واستخدام وظيفتها في الجوانب اليمنى.
الاختلاف الوحيد هو أن وظيفة الجانب الأيمن func (t، y) تقبل متغيرًا مستقلًا كوسيطة أولى ، وقائمة قيم الوظائف المطلوبة كالثانية. على سبيل المثال ، يؤدي التسلسل التالي من التعليمات إلى إنشاء ODE يمثل مهمة Cauchy.
طريقة رونج - كوتاعند إنشاء الخوارزميات العددية ، نفترض وجود حل لهذه المشكلة التفاضلية ، وهو فريد وله خصائص النعومة اللازمة.
في الحل العددي لمشكلة كوشي
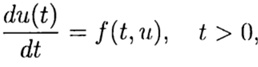
(2)
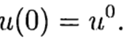
(3)
وفقًا للحل المعروف عند النقطة t = 0 ، من الضروري إيجاد حل من المعادلة (3) لـ t الأخرى. في الحل العددي للمشكلة (2) ، (3) ، سنستخدم شبكة موحدة ، من أجل البساطة ، في المتغير t بخطوة t> 0.
حل تقريبي للمشكلة (2) ، (3) عند النقطة
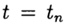
يدل
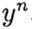
. تتقارب الطريقة عند نقطة
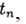
إذا
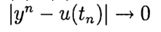
في

. هذه الطريقة لها دقة pth إذا
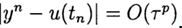
، p> 0 لـ

. إن أبسط مخطط فرق لحل تقريبي للمشكلة (2) ، (3) هو
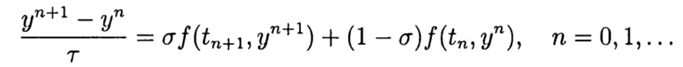
(4)
في
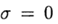
لدينا طريقة صريحة وفي هذه الحالة يقارب مخطط الفرق المعادلة (2) بالترتيب الأول. تصميم متماثل
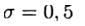
في (4) لديه ترتيب تقريبي ثان. ينتمي هذا المخطط إلى فئة ضمنية - لتحديد الحل التقريبي على طبقة جديدة ، من الضروري حل المشكلة غير الخطية.
من الملائم إنشاء مخططات تقريبية صريحة من الدرجة الثانية والأعلى استنادًا إلى طريقة مصحح التنبؤ. في مرحلة التوقع (التنبؤ) ، يتم استخدام مخطط صريح.
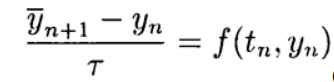
(5)
وفي مرحلة المصحح (التحسين) ، رسم تخطيطي
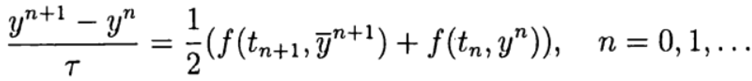
في طريقة Runge - Kutta ذات الخطوة الواحدة ، يتم تحقيق أفكار مصحح التوقع بشكل كامل. هذه الطريقة مكتوبة بشكل عام:
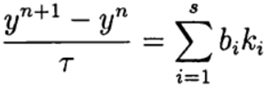
(6)
أين
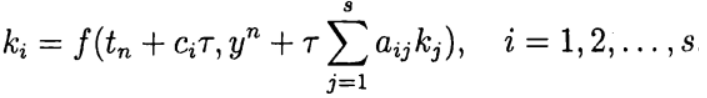
تعتمد الصيغة (6) على حسابات s للدالة f وتسمى s-stage. إذا
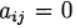
في
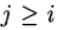
لدينا طريقة رونج - كوتا الصريحة. إذا
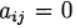
ل j> 1 و
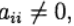
ثم
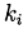
محدد ضمنيا من المعادلة:
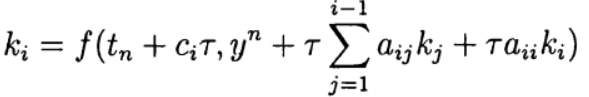
(7)
يتم الحديث عن طريقة Runge - Kutta على أنها ضمنية قطريًا. معلمات
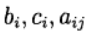
تحديد متغير لطريقة رونج - كوتا. تم استخدام التمثيل التالي للطريقة (جدول الجزار)
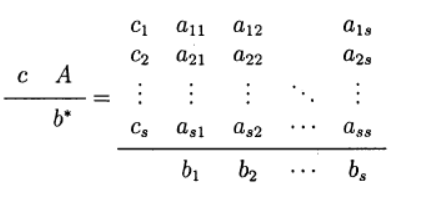
واحدة من أكثرها شيوعًا هي طريقة Runge - Kutta الصريحة من الدرجة الرابعة.
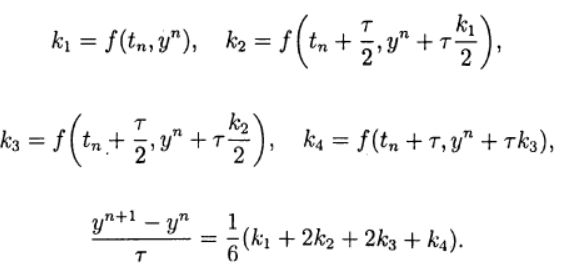
(8)
طريقة رونج - كوتا - فيلبيرجأعطي قيمة المعاملات المحسوبة
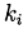
الطريقة

(9)
في ضوء الرقم (9) يكون الحل العام بالصيغة التالية:
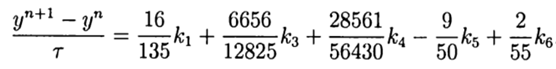
(10)
يوفر هذا الحل الترتيب الخامس من الدقة ، ويبقى لتكييفه مع Python.
تجربة حسابية لتحديد الخطأ المطلق للحل العددي لمعادلة تفاضلية غير خطية 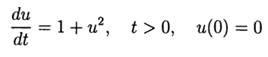 باستخدام كل من وظائف def odein () و def oden () للوحدة النمطية scipy.integrate وطرق Runge - Kutta و Runge - Kutta - Felberg المكيفة مع Python
باستخدام كل من وظائف def odein () و def oden () للوحدة النمطية scipy.integrate وطرق Runge - Kutta و Runge - Kutta - Felberg المكيفة مع Python
قائمة البرنامجfrom numpy import* import matplotlib.pyplot as plt from scipy.integrate import * def odein():
نحصل على:
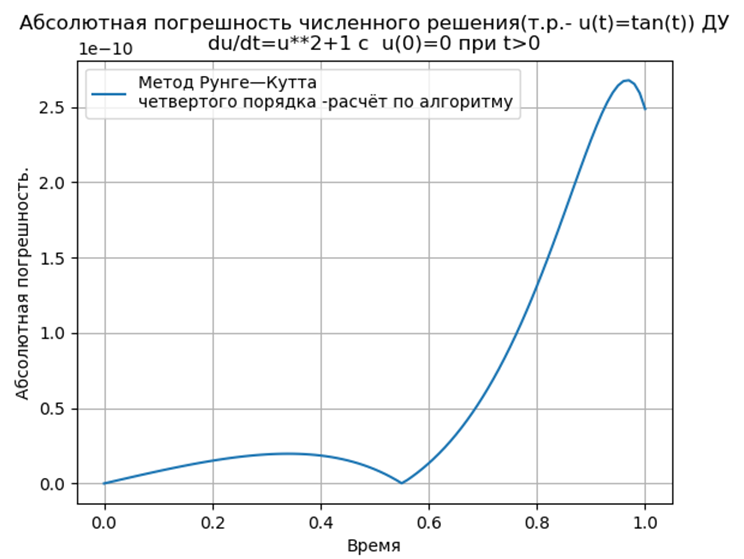
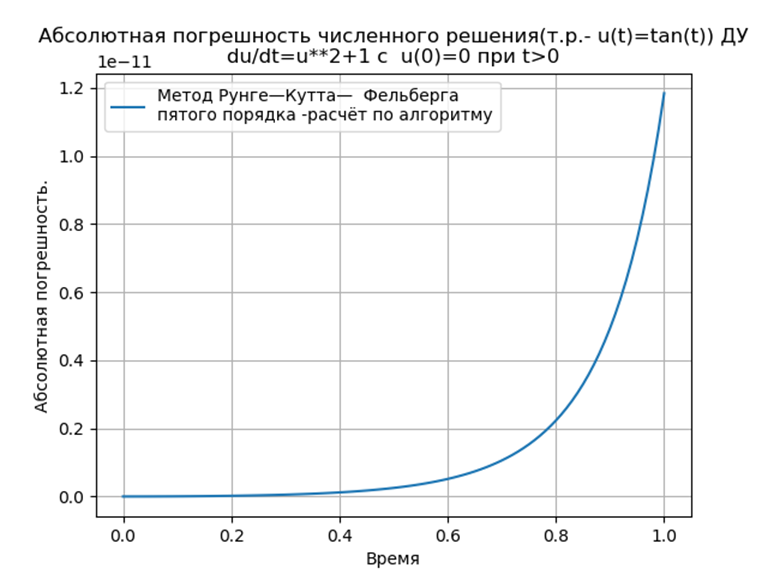
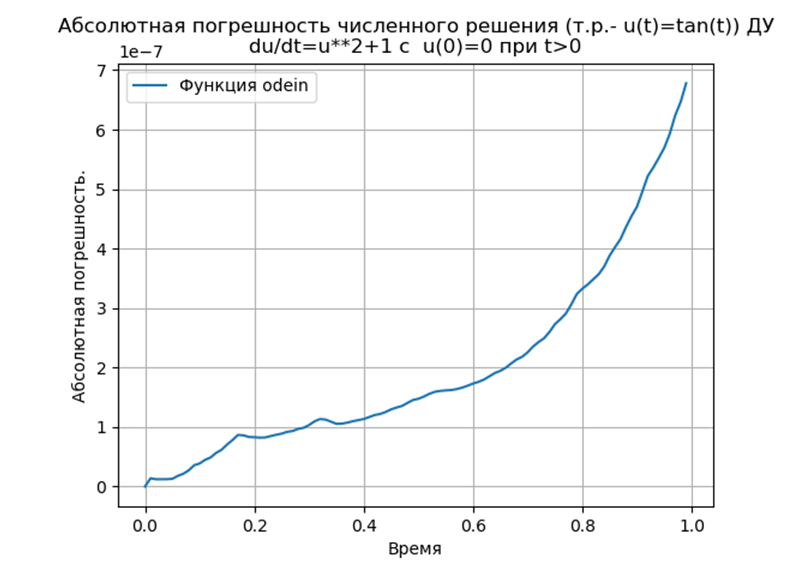
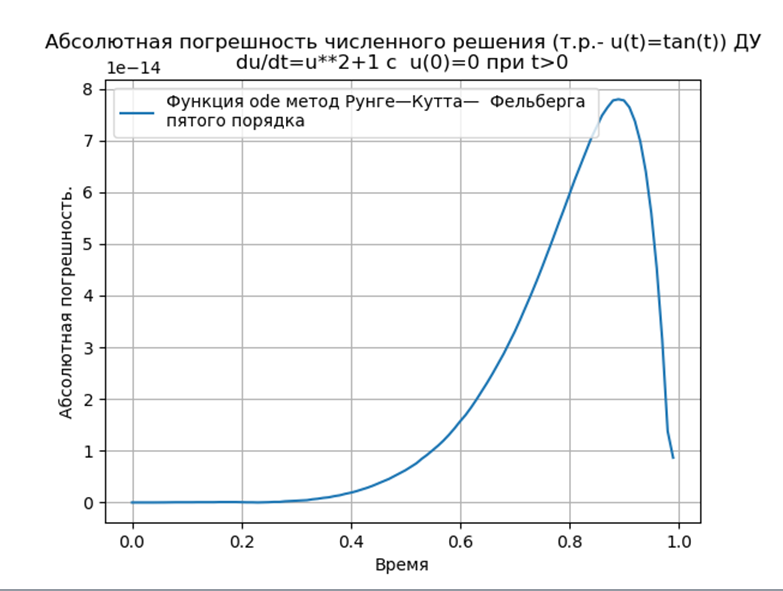 الخلاصة:
الخلاصة:إن طرق Runge المتكيفة مع Python - Kutta و Runge - Kutta - Felberg لها مطلق مطلق أقل من حل باستخدام وظيفة odeint ، ولكن أكثر من حل باستخدام وظيفة edu. من الضروري إجراء دراسة الأداء.
تجربة عددية تقارن سرعة الحل العددي لـ SDE عند استخدام وظيفة ode مع خاصية dopri5 (طريقة Runge - Kutta من الترتيب الخامس) وباستخدام طريقة Runge - Kutta - Felberg المكيفة مع Python
يتم إجراء تحليل مقارن باستخدام مشكلة النموذج الواردة في [2] كمثال. لكي لا أكرر المصدر ، سأقدم صياغة وحل مشكلة النموذج من [2].
دعونا نحل مشكلة كوشي ، التي تصف حركة الجسم الملقي بسرعة أولية v0 بزاوية α إلى الأفق على افتراض أن مقاومة الهواء تتناسب مع مربع السرعة. في شكل متجه ، فإن معادلة الحركة لها الشكل
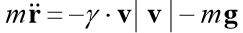
أين
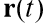
هو نصف قطر متجه الجسم المتحرك ،
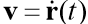
هو ناقل سرعة الجسم ،
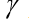
- معامل السحب ، المتجه
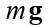
قوى وزن الجسم m، g - تسارع الجاذبية.
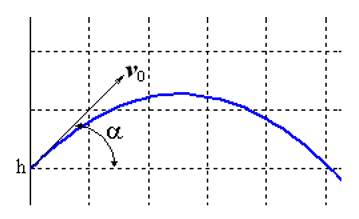
تكمن خصوصية هذه المهمة في أن الحركة تنتهي عند نقطة غير معروفة سابقًا في الوقت الذي يسقط فيه الجسم على الأرض. إذا تم تعيينه
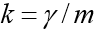
ثم في شكل إحداثيات لدينا نظام من المعادلات:
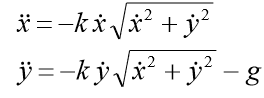
يجب إضافة الشروط الأولية إلى النظام:
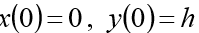
(الارتفاع الأولي)
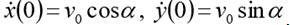
. ضع
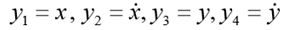
. ثم يأخذ نظام ODE من الدرجة الأولى المقابل الشكل التالي:
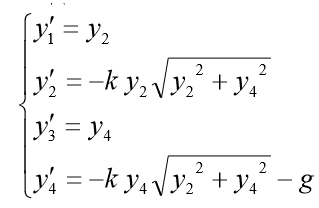
لمشكلة النموذج وضعنا
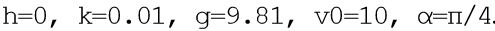
. مع حذف وصف موسع إلى حد ما للبرنامج ، سأقدم فقط قائمة من التعليقات التي أعتقد أن مبدأ تشغيلها سيكون واضحًا. أضاف البرنامج عد تنازلي للتحليل المقارن.
قائمة البرنامج import numpy as np import matplotlib.pyplot as plt import time start = time.time() from scipy.integrate import ode ts = [ ] ys = [ ] FlightTime, Distance, Height =0,0,0 y4old=0 def fout(t, y):
نحصل على:
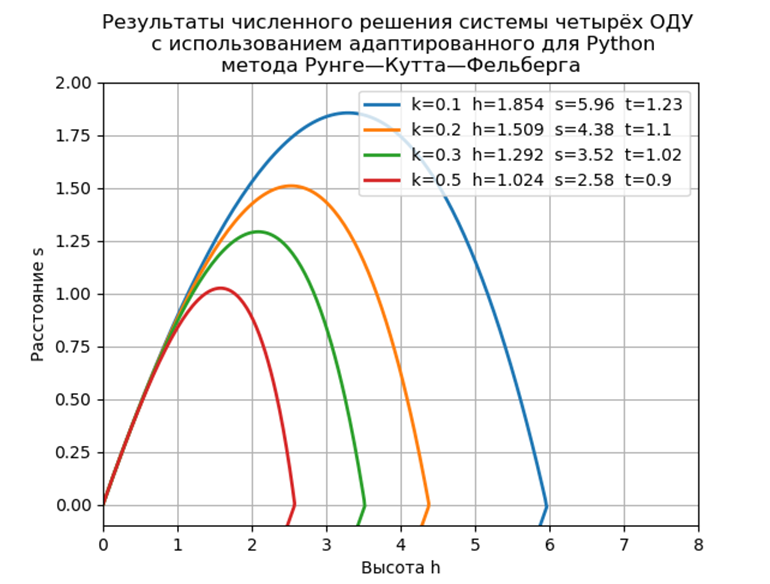
زمن الرحلة = 1.2316 المسافة = 5.9829 الارتفاع = 1.8542
زمن الرحلة = 1.1016 المسافة = 4.3830 الارتفاع = 1.5088
زمن الرحلة = 1.0197 المسافة = 3.5265 الارتفاع = 1.2912
زمن الرحلة = 0.9068 المسافة = 2.5842 الارتفاع = 1.0240
الوقت لمشكلة النموذج: 0.454787
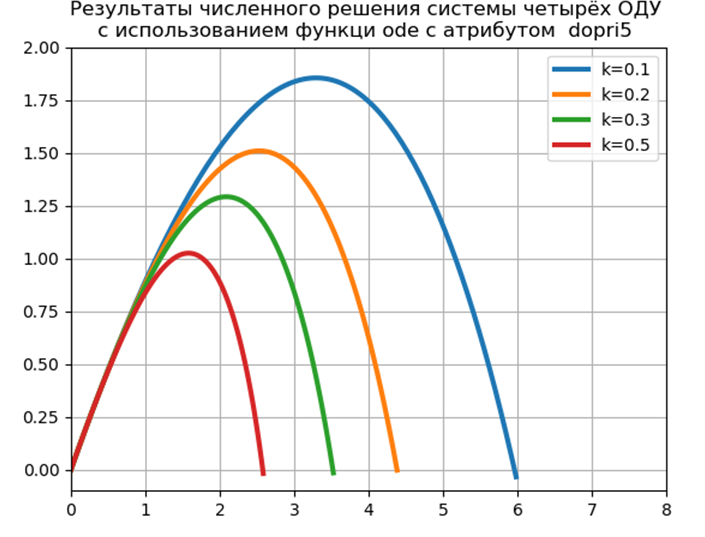
لتنفيذ حل رقمي لـ CDS باستخدام أدوات Python دون استخدام وحدات خاصة ، اقترحت وتحققت من الوظيفة التالية:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6توفر دالة الزيادة (f ، t ، y ، tau) الترتيب الخامس لطريقة الحل العددي. يمكن العثور على ميزات أخرى للبرنامج في القائمة التالية:
قائمة البرنامج from numpy import* import matplotlib.pyplot as plt import time start = time.time() def rungeKutta(f, to, yo, tEnd, tau): def increment(f, t, y, tau):
نحصل على:
الوقت لمشكلة النموذج: 0.259927
 الخلاصة
الخلاصةإن تنفيذ البرنامج المقترح لمشكلة النموذج دون استخدام وحدات خاصة لديه أداء أسرع مرتين تقريبًا من وظيفة ode ، ولكن يجب ألا ننسى أن ode لديه دقة أعلى للحل العددي وإمكانية اختيار طريقة الحل.
حل مشكلة قيمة الحدود مع شروط الحدود المفصولة بالخيوط
نعطي مثالاً لمشكلة قيمة حدود معينة مع شروط الحدود المفصولة بالخيوط:
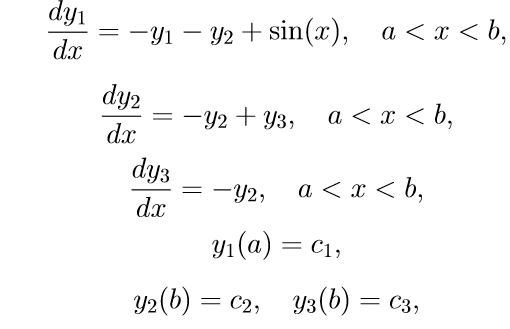
(11)
لحل المشكلة (11) ، نستخدم الخوارزمية التالية:
1. نحل المعادلات الثلاثة الأولى غير المتجانسة للنظام (11) بالشروط الأولية

نقدم ترميزًا لحل مشكلة كوشي:
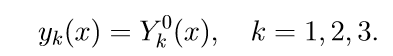
2. نحل المعادلات الثلاثة الأولى المتجانسة للنظام (11) بالشروط الأولية
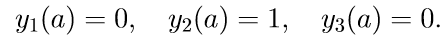
نقدم ترميزًا لحل مشكلة كوشي:
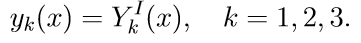
3. نحل المعادلات الثلاثة الأولى المتجانسة للنظام (11) بالشروط الأولية
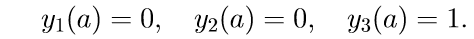
نقدم ترميزًا لحل مشكلة كوشي:

4. الحل العام لمشكلة القيمة الحدية (11) باستخدام حلول مشاكل كوشي مكتوب كمجموعة خطية من الحلول:
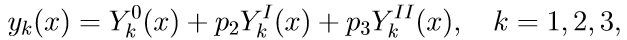
حيث p2 و p3 بعض المعلمات غير معروفة.
5. لتحديد المعلمات p2 ، p3 ، نستخدم الشروط الحدية للمعادلتين الأخيرتين (11) ، أي شروط x = b. استبدال ، نحصل على نظام المعادلات الخطية فيما يتعلق غير معروف p2 ، p3:
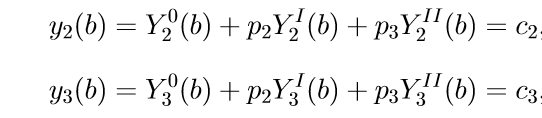
(12)
حل (12) ، نحصل على العلاقات ل 2 ، ص 3.
باستخدام الخوارزمية أعلاه باستخدام طريقة Runge - Kutta - Felberg ، نحصل على البرنامج التالي:
نحصل على:
y0 [0] = 0.0
y1 [0] = 1.0
y2 [0] = 0.7156448588231397
y3 [0] = 1.324566562303714
y0 [N-1] = 0.9900000000000007
y1 [N-1] = 0.1747719838716767
y2 [N-1] = 0.8
y3 [N-1] = 0.5000000000000001
الوقت لمشكلة النموذج: 0.070878
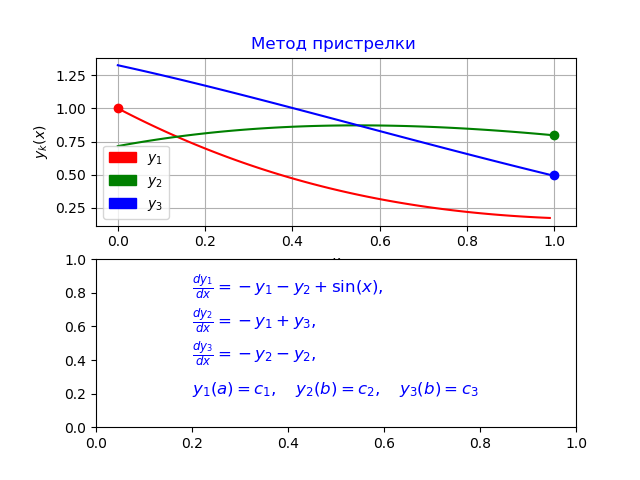
الخلاصة
يختلف البرنامج الذي طورته عن الخطأ الوارد في [3] ، والذي يؤكد التحليل المقارن لوظيفة odeint المعطاة في بداية المقالة باستخدام طريقة Runge - Kutta - Felberg المنفذة في Python.
المراجع:
1.
الحل العددي للنماذج الرياضية للكائنات المحددة بواسطة أنظمة مركبة من المعادلات التفاضلية.2.
مقدمة في بايثون العلمي.3. ن. بولياكوفا ، إ. Shiryaeva Python 3. إنشاء واجهة مستخدم رسومية (باستخدام مثال حل مشكلة القيمة الحدودية للمعادلات التفاضلية الخطية بطريقة التصوير). روستوف نا دون 2017.