مناور "يدوي"

ذات مرة ، خلال سنتي الثانية في الجامعة ، كلفتني بمهمة: طهي شيء ما "من نوع" من أجل تأكيد الرتبة العالية لـ "مهندس الروبوتات المستقبلي". في هذه المذكرة المذهلة ، ذهبت إلى أعماق الوعي للبحث عن الأفكار. بعد رحلة قصيرة ، نشأت فكرة حول الجهاز ، وأريد أن أشاركه في نظرية الإنشاء مع الجمهور.

جوهر التنمية هو هذا. ضع في اعتبارك المعالج المعتاد خماسي المحاور (يظهر المخطط الهيكلي الحركي في الشكل أدناه). إن قدراته عند التحرك في الفضاء واسعة: فهي قادرة على القيام بحركات في 5 إحداثيات ، وفي نفس الوقت ، أي 3 إحداثيات على طول محاور XYZ الثلاثة وتدور حول اثنين منها. في هذه الحالة ، يمكن لعنصر العمل في المعالج أن يشغل أي منصب في مساحة العمل وفي نفس الوقت يحافظ على الاتجاه المطلوب لهيئة العمل (لا يحسب دوران عنصر العمل حول محوره).



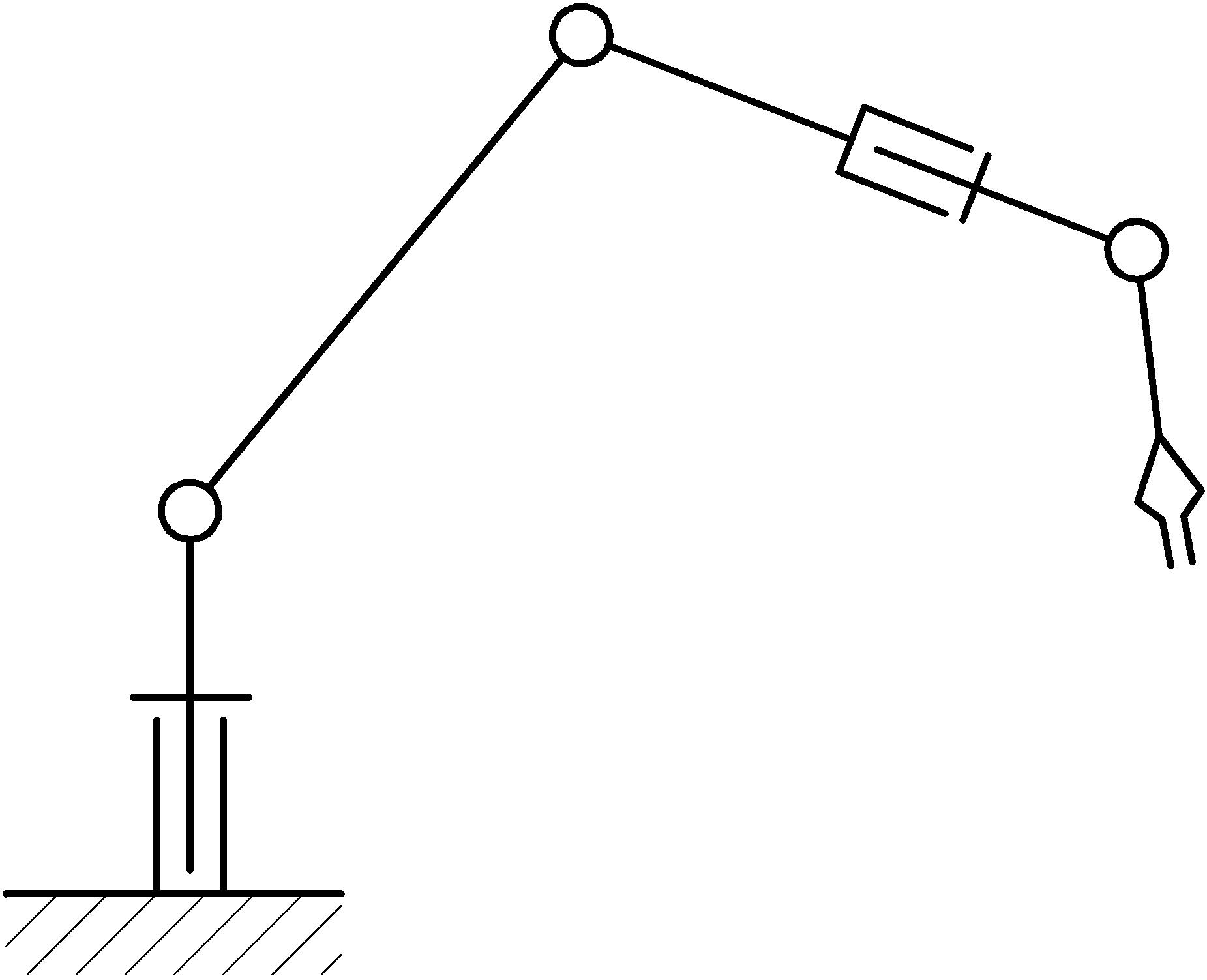
يتعلق هذا التصميم بمتلاعبين من نوع مجسم وبالتالي فهو قادر تقريبًا ، بالطبع ، على إعادة إنتاج حركة اليد البشرية. الجدل حول هذه الأطروحة ، جاءت الفكرة للتو أنه سيكون من المثير للاهتمام جعل المتلاعب ينسخ حركات يدي عن بعد في الوقت الحقيقي. حتى أضع جهاز استشعار على يدي يقرأ حركات اليد (الخطية والزاوية) ، وهذا الشيء الميكانيكي سيكررها بعدي. نظرًا لأن المناور يمكنه أداء وظائف تحريك وتوجيه الجسم العامل ، لذلك بمساعدة الشخص يمكن أن يتحرك ويوجه راحة يده ، وبالتالي فإن هاتين العمليتين متشابهتان ويمكن تمثيلهما كعملية مشتركة واحدة - التقاط حركة اليد من قبل المناور في الوقت الحقيقي.


هذا يكمل بيان المشكلة. الآن دعنا نحلل المهمة (اللغة لا تتحول إلى تسميتها "مهمة فنية"). من الضروري تطوير جهازين مستقلين هيكليا: المعالج نفسه وجهاز تتبع الحركة ، الذي يتم تركيبه على الذراع. وسيتبع ذلك عملية تستغرق وقتًا طويلاً لإنشاء أوصاف رياضية ، وتجميع خوارزمية وكتابة برمجيات. نقسم المشروع إلى ثلاثة أجزاء:

1. تطوير مناور
2. تطوير جهاز لتتبع حركة الذراع
3. كل شيء آخر

باختصار عن كل مرحلة:

1. كل شيء تافه هنا ... في CAD ، نقوم بتصميم الهيكل وتنفيذ رسومات الأجزاء والتصنيع ، ثم تجميعها. ثم نقوم بحساب الكينماتيكا ونكتب برمجياتنا الخاصة ، والتي ستخفي المكالمات ذات المستوى المنخفض إلى محركات الأقراص.
2. في هذه المرحلة ، نحدد نوع المستشعرات ، ونصمم مخططًا دائريًا ، ونصنع لوحة دوائر مطبوعة ، ونطور خوارزمية لتحديد الموقع في الفضاء ، ونكتب البرامج.
3. في الواقع ، لما كانت المراحل السابقة - لجعل المتلاعب يطيع المالك. هنا أقوم بتطوير خوارزمية لتحويل الإحداثيات إلى مجال عمل المعالج.

1. تطوير مناور

في هذا المشروع ، كما ذكر أعلاه ، نستخدم مناورًا بخمس درجات من الحرية. مثل هذا العدد من درجات الحرية يكفي ، لأن وهي تشمل ثلاث عمليات إزاحة خطية واثنتين دورانيتين. الأخيرين ضروريان لتوجيه جسم العمل ، حيث يمكن تحديد اتجاه PO في الفضاء في شكل ناقل ، ويمكن بالتأكيد استعادة الناقل من زاويتين للدوران (مع عدم مراعاة الطول). في هذه الحالة ، نحتاج إلى خمسة إحداثيات معممة تساوي عدد المحاور.

ترتبط روابط المناور بأزواج حركية دورانية من الدرجة الخامسة. تصميم المناور قياسي لنوعه (يتم عرض المخطط الحركي في بداية المقالة). تحتوي على سرير ثابت ، يتم توصيل نظام الإحداثيات الأساسي به ، وحامل دوار ، يتم إرفاق الروابط المنقولة المتبقية به ، متصلة في سلسلة. يتم إرفاق جسم عامل بالرابط النهائي (شفة) ، في هذه الحالة تقليده في شكل مؤشر على شكل سهم (انظر الصورة أدناه).




تم بناء النموذج ثلاثي الأبعاد في CAD "Compass 3D". أجزاء المواد - 4 مم من الخشب الرقائقي و PLA للأجزاء البلاستيكية. تم قطع أجزاء من الخشب الرقائقي على جهاز ليزر ، وتم طباعة أجزاء من البلاستيك على طابعة ثلاثية الأبعاد. يتم استخدام الماكينات الرقمية Dynamixel AX-12 كمحركات لمحور. يشبه مظهر المناور حشرة دنيئة ، حصل منها على لقب "كومار".

الوصف الرياضي لعلم الحركة

في هذه المرحلة ، من الضروري حساب الكينماتيكا المباشرة والعكسية للمتلاعب. وتتمثل المهمة المباشرة في تحديد موضع الروابط بالنسبة لبعض نظام الإحداثيات الأساسي باستخدام القيم المعروفة للإحداثيات المعممة (في هذه الحالة ، زوايا دوران الروابط). تسمى المهمة العكسية لها الكينماتيكا المعكوسة أو العكسية ، وتتكون من تحديد معلمات الإحداثيات المعممة لتحقيق الموضع المطلوب وتوجيه الجسم العامل في المعالج.

لنبدأ بحساب الكينماتيكا العكسية. دعونا نرسم المخطط الهندسي للمتلاعب ، الذي ستكون فيه العلاقات الهندسية التي تهمنا واضحة.



يتم تمثيل الموضع المطلوب بواسطة متجه نصف القطر $$$\ vec {r}$ . يجدر شرح لماذا ناقلات $$$\ vec {r}$ مرسومة إلى نقطة الحافة ، وليس إلى نقطة نهاية RO. بما أن اتجاه الجسم العامل معروف لنا مسبقًا (أنا شخصياً أحدده وفقًا لبعض المتطلبات) ، فمن الضروري أن تكون نقطة الشفة في المكان الصحيح ، المشار إليها كمتجه $$$\ vec {r}$ . يتم الحصول على هذا المتجه عن طريق الطرح من متجه نصف القطر $$$\ vec {R}$ مرسومة حتى نقطة نهاية PO ، متجه اتجاهها $$$\ vec {v_0}$ ، بالنسبة إلى BSK ، أي:

$$

$$\ vec {r} = \ vec {R} - \ vec {v_0}$$

خذ بعين الاعتبار انتقال نقطة الشفة إلى الموضع المطلوب. يتم ذلك عن طريق تناوب الروابط a و b (صورتهم على شكل ناقلات) في المفصلات A و B و C. يتم وضع أصل نظام إحداثيات القاعدة (BSC) عند نقطة المفصلة B. يتم توجيه محور دوران المفصلة A على طول المحور Z ، ويتم توجيه المحورين B و C بشكل عمودي على Z.

عندما يتم استيفاء جميع الشكليات ، دعنا نصل إلى النقطة. لحل مشكلة الحركية العكسية ، استخدمت نهجًا هندسيًا بسبب بساطة تصميم المعالج. من الهندسة يمكن ملاحظة أن المتجه $$$\ vec {r}$ يساوي مجموع ناقلات الارتباط $$$\ vec {a}$ و $$$\ vec {b}$ . الزوايا $$$\ theta$ ، $$$\ gamma_1$ ، $$$\ gamma_2$ - زوايا دوران الوصلات A و B و C على التوالي.
النظر في مثلث يحده ناقلات $$$\ vec {r}$ ، $$$\ vec {a}$ و $$$\ vec {b}$ . من هذا المثلث ، من خلال نظرية جيب التمام ، نجد الزوايا $$$\ alpha$ و $$$\ بيتا$ . دع أطوال ناقلات تساوي:

$$

$$| \ vec {r} | = r \ quad | \ vec {a} | = a \ quad | \ vec {b} | = b$$

نكتب نظرية جيب التمام بشأن الزوايا المطلوبة:

$$

$$b ^ 2 = a ^ 2 + r ^ 2-2ar \ cos (\ alpha) \\ r ^ 2 = a ^ 2 + b ^ 2-2ab \ cos (\ beta)$$

عبر عن الزوايا $$$\ alpha$ و $$$\ بيتا$ :

$$

$$\ alpha = \ arccos \ left (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ar} \ right) \ quad \ beta = \ arccos \ left (\ frac {a ^ 2 + b ^ 2 -r ^ 2} {2ab} \ right)$$

يمكن أن نرى من الرسم البياني الهندسي ما يلي:

$$

$$\ theta = \ arctan = \ left (\ frac {r_y} {r_x} \ right) \ quad \ omega = \ arcsin = \ left (\ frac {r_z} {r} \ right)$$

ثم:

$$

$$\ gamma_1 = \ omega + \ alpha \ quad \ gamma_2 = 180 ^ \ circ- \ beta$$

أخيرًا ، يتم إجراء الانتقال من إحداثيات خطية إلى زوايا دوران الروابط بواسطة الصيغ:

$$

$$\ theta = arctan \ left (\ frac {r_y} {r_x} \ right) \\ \ gamma_1 = arcsin \ left (\ frac {r_z} {r} \ right) + arccos \ left (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ab} \ right) \\ \ gamma_2 = 180 ^ \ circ-arccos \ left (\ frac {a ^ 2 + b ^ 2-r ^ 2} {2ar} \ right)$$

الآن بعد أن قمت بنقل نقطة الشفة إلى الموضع المطلوب ، تحتاج إلى توجيه جسم العمل بشكل صحيح. للقيام بذلك ، تحتاج إلى معرفة إحداثيات الناقل $$$\ vec {v}$ بالنسبة إلى نقطة الحافة ، أي الإحداثيات على أساس نظام الإحداثيات المحلي (LSC) - $$${E '}$ ، التي تقع بدايتها عند نقطة شفة المعالج.

$$

$$E '= \ left [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ right]$$

ناقل $$$\ vec {x} '$ إخراج الارتباط ب ، متجه $$$\ vec {y} '$ - على طول المحور الدوار f1 .
لإيجاد أساس $$$E '$ نحدد مصفوفة الانتقال من BSK (مع الأساس $$$E_0$ ) و LSK. يتم الحصول على هذه المصفوفة من خلال مجموعة من الدورات في المفصلات A و B و C :

$$

$$E '= CE_0$$

أين

$$

$$C = R_CR_BR_A$$

لأن مصفوفة $$$E_0$ واحد ، ثم:

$$

$$E '= C = R_CR_BR_A$$

مصفوفة $$$C$ يتم حسابه بضرب مصفوفات الدوران حول المحور بزاوية .
نحدد دالة تحسب هذه المصفوفة:

$$

$$f = axisAngle2rotMat (المحور ، الزاوية)$$

يتم أخذ المحور في شكل متجه كعمود من المصفوفة التي تم الحصول عليها من خلال الدورات السابقة ، ويتم حساب الزوايا بالفعل أعلاه.

$$

$$C_A = axisAngle2rotMat (E_0 ^ {\ langle3 \ rangle}، \ theta) \\ C_ {BA} = R_BC_A = axisAngle2rotMat (C_A ^ {\ langle2 \ rangle}، \ gamma_1) C_A \\ C_ {CBA} = R_CC_ { BA} = axisAngle2rotMat (C_ {BA} ^ {\ langle2 \ rangle}، \ gamma_1) C_ {BA}$$

نتيجة لذلك ، نحصل على:

$$

$$C = C_ {CBA} \ quad E '= C$$

دع ناقل الجسم العامل في BSK $$$\ vec {v_0}$ . ثم المساواة صحيحة:

$$

$$\ vec {v_0} = E '\ vec {v}$$

من هنا نعبر $$$\ vec {v}$ - ناقل الجسم العامل في الأساس $$$E '$ ، أي نسبة إلى شفة:

$$

$$\ vec {v} = E '^ T \ vec {v_0}$$

الآن ، بمعرفة متجه PO ، يمكننا حساب زوايا دوران محوري التوجيه f1 و f2


لنقل أمر الشراء إلى موضع معين ، تحتاج إلى إجراء دوران في الزوايا $$$\ varphi_1$ و $$$\ varphi_2$ . يوضح الشكل ذلك

$$

$$\ varphi_1 = arctan \ left (\ frac {v_y} {v_z} \ right) \ quad \ varphi_2 = arcsin \ left (\ frac {\ sqrt {v_y ^ 2 + v_z ^ 2}} {V} \ right)$$

أين $$$V = | \ vec {v} | = \ sqrt {v_x ^ 2 + v_y ^ 2 + v_z ^ 2}$ - طول الجسم العامل ،
$$$v_x ، v_y ، v_z$ - إحداثيات ناقلات $$$\ vec {v}$ .

ينقسم برنامج المعالج إلى مستويين ، العلوي والسفلي. تم كتابة المستوى العلوي في Matlab في شكل مكتبة وأساليب قيادة مختلفة ، الجزء السفلي - على متحكم Atmega328. مهمة المستوى العلوي هي صياغة الأوامر المرسلة إلى وحدة التحكم الدقيقة. تتمثل مهمته في الحصول على الفريق ، ووفقًا له ، قم بتثبيت محركات الأقراص في الموضع الصحيح. في هذا النموذج ، تبين أن نظام التحكم موثوق به (حتى الآن ...) وملائم للاستخدام.


تكون صياغة الأمر والإرسال من المستوى العلوي كما يلي: يستدعي المستخدم في نافذة الأوامر Matlab وظيفة من المكتبة (على سبيل المثال ، وظيفة الانتقال ببساطة إلى نقطة) ، يشير إلى الحجج الضرورية (عادة ما تكون هذه الإحداثيات وتوجيه أمر الشراء). بعد الاعتبارات الرياضية الموضحة أعلاه ، والمسجلة في المكتبة ، يتم حساب زوايا دوران المحاور ، وإذا لزم الأمر ، يتم حساب سرعة الدوران. بعد بروتوكول بسيط ، نقوم بتجميع الأمر وإرساله إلى وحدة التحكم الدقيقة ذات المستوى الأدنى عبر منفذ COM التسلسلي.

بضع كلمات عن المكتبة المكتوبة. لديها الوظائف التالية تحت تصرفها:

1. وظائف الاتصال التسلسلي
2. وظائف متحركة

• إلى حد ما ، مع سرعة ثابتة لجميع محركات الأقراص
• إلى نقطة ، مع توقف نهائي لجميع محركات الأقراص (يتم تحديد سرعة محرك الأقراص بما يتناسب مع زاوية التدوير الخاصة به وأكبرها. وبالتالي ، في نهاية النهج إلى النقطة ، تتوقف جميع محركات الأقراص عن الحركة)
• إلى حد ما ، مع حركة سلسة لكل محرك أقراص (في هذه الحالة ، يظهر الرسم البياني للسرعة على شكل شبه منحرف مع مناطق التسارع والسرعة الثابتة والكبح)
  
  
  الرسم البياني

  

  
  
  
  
• إلى حد ما ، وفقًا لزوايا دوران المحاور المحددة يدويًا وسرعة الدوران

يمكن بالطبع توسيع قائمة الوظائف ، ولكن هذه الوظيفة كانت كافية لحل المشكلة التي تم تصميم معالجها بشكل مباشر.

يوضح الفيديو تشغيل المتلاعب.

2. تطوير جهاز لتتبع حركة الذراع

انتقل إلى الخطوة التالية. هنا ستحتاج إلى تصميم جهاز خاص يمكنه تتبع الموقع في راحة يدك في الوقت الفعلي. أيضا ، تسمى هذه العملية "التقاط الحركة". لتنفيذ الخطة ، قررت استخدام نظام الملاحة بالقصور الذاتي (SINS) القائم على ثلاثة أجهزة استشعار: الجيروسكوب ومقياس التسارع ومقياس المغناطيسية. حفنة من هذه المستشعرات تسمى IMU - مستشعر (في الترجمة ، هذا هو نفس SINS).

أولاً ، صممت لوحة دوائر مطبوعة بالوظائف التي أحتاجها ، والتي وضعت عليها أجهزة الاستشعار الثلاثة هذه. بصفتي متحكم المعالجة ، اخترت (أو بالأحرى أخذت ما هو) متحكم Atmega2560. تستخدم أجهزة الاستشعار الشائعة والرخيصة في السوق الصينية. هذه هي أجهزة الاستشعار المقترنة جيروسكوب ثلاثي المحاور ومقياس التسارع MPU6050 ومقياس المغناطيسية HMC5883l.



إن الخوارزمية لحساب الموقع في الفضاء بسيطة للغاية: أولاً ، نحدد الاتجاه في شكل أساس لنظام الإحداثيات المحلي (LSC) ، المرتبط بأجهزة الاستشعار ، وفي النهاية مع راحة اليد.



يتم تحديد الاتجاه بالنسبة إلى نظام الإحداثيات الأولي (NSC) ، وهو في الأساس الموضع الأولي للجهاز في وقت التشغيل. تتكون قواعد NSC و LSC من ناقلات أعمدة من orth:

$$

$$E_0 = \ left [\ vec {X} \ \ vec {Y} \ \ vec {Z} \ right] = \ left [\ start {array} {cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] \\ E '= \ left [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ right]$$

ترتبط بالنسبة:

$$

$$E '= CE_0$$

أين $$$C$ هي مصفوفة انتقالية ، كما أنها مصفوفة دوران في الفضاء. نعتبر أساس مجلس الأمن القومي بمثابة مصفوفة الهوية. لذلك

$$

$$E '= C$$

.
بعد ذلك ، ناقل التسارع $$$\ vec {A}$ ، والمعروف فيما يتعلق بـ LSC ، يجب تحديده في NSC. يتم ذلك عن طريق ضرب متجه عمود التسارع في أساس LSC:

$$

$$\ vec {A} = E '\ vec {A}'$$

ثم نقوم بدمج متجه التسارع الذي تم الحصول عليه مرتين بمرور الوقت والحصول على المسافة ، أي إحداثيات:

$$

$$\ vec {r} = \ iint \ vec {A} dt$$

كانت المحاولات الأولى لتنفيذ هذه الخوارزمية ساذجة للغاية ... السذاجة هي أنني اعتبرت أنه من الممكن فقط من الجيروسكوب ، باستخدام التكامل المنفصل ، للحصول على مصفوفة دوران حول المحور. يمكن اعتبار المحور في هذه الحالة كمحرك زائف للسرعة الزاوية ، ومكوناته (الإسقاط على المحور) هي الإخراج من مستشعر الدوران. ويتم الحصول على الزاوية ، بدورها ، من خلال دمج وحدة المتجه. اختفى الحماس والحماس المبدئي عندما رأيت حجمًا وحشيًا كبيرًا ، يسمى "الانحراف الصفري" ، الناجم عن الخطأ المتراكم بسبب خطأ الاندماج المنفصل والضوضاء الداخلية للمستشعر. حتى ذلك الحين ، كانت لدي أفكار أنه وفقًا لمقياس التسارع ، الذي يظهر في بقية النواقل ، معكوس متجه تسارع الجاذبية (يشار إليه فيما بعد باسم ناقل الجاذبية) ، يمكنك إجراء تصحيح المصفوفة ، ولكن هنا يوجد عدم يقين مرتبط بحقيقة أن التصحيح ممكن فقط حتى دوران الزاوية حول المحور Z. سيكتمل التصحيح إذا كان من الممكن استعادة مصفوفة الدوران بطريقة بديلة ، أي بدون استخدام بيانات الدوران.


ثم من الضروري استخدام عامل آخر يمكن من خلاله إجراء تعديل كامل للوضع. هذا العامل هو المجال المغناطيسي للأرض ، والذي ، إلى جانب الجاذبية عند نقطة واحدة على الكوكب ، لا يتغير بمرور الوقت (بالطبع على المدى القصير). يتم قياسه باستخدام جهاز استشعار HMC5883l المذكور أعلاه. في هذه الحالة ، لدينا متجهان ، يكفيان لتحديد الموقع في الفضاء بالنسبة إليهما.

الآن يطرح سؤال منطقي - "كيف نفعل ذلك؟" بعد محاولات فاشلة للإجابة على هذا السؤال ، تسلقت على الإنترنت بنفسي ، حيث وجدت المعلومات التي احتاجها. تنشأ مهمة تحديد الاتجاه في الفضاء وفقًا لثلاثة قياسات (السرعة الزاوية ومتجه الجاذبية وناقل المجال المغناطيسي) أيضًا في تصميم طائرات الهواة (على سبيل المثال ، المروحيات) ، لذلك تم حل هذه المشكلة بشكل متكرر بطرق مختلفة. إحدى الطرق الشائعة هي ما يسمى بفلتر Majwick (Sebastian OH Madgwick). بعد قراءة المقال الأصلي وعدم فهم اللغة الإنجليزية ، تحولت إلى ترجمة رائعة (بفضل المؤلف على العمل المنجز). أثناء الخوض في دراسة المقالة ، كان لدي في كثير من الأحيان فكرة محاولة كتابة خوارزمية تصفية تحديد الموقف الخاصة بي ، بالنظر إلى أنه في هذه اللحظة زاد مستوى معرفتي في هذا المجال بشكل ملحوظ. من أجل الاهتمام ، "اخترع دراجة"! وأنا "اخترعت" ذلك. أدناه أعطي تفكيري.

تستخدم الخوارزمية قراءات جميع أجهزة الاستشعار الثلاثة. دعني أذكرك بأن مهمة الخوارزمية هي حساب اتجاه الجسم وتعويض الانحراف الصفري للجيروسكوب ، بالنظر إلى الزوج المحدد من مقياس التسارع ومقياس المغناطيسية. كأداة رياضية تصف الموقف ، يتم استخدام quaternion ، لأنه إنها ملائمة من حيث بناء وتحسين الخوارزمية وتتطلب عمليات حسابية أقل لحسابها ، على عكس المصفوفات. رباعي الدوران في الفضاء على النحو التالي:

$$

$$q = \ left [q_1 \ q_2 \ q_3 \ q_4 \ right]$$

معرفة محور الدوران الموصوف بالنواقل المعيارية $$$\ vec {v} = \ left [v_x \ v_y \ v_z \ right]$ وزاوية $$$\ varphi$ (حيث يأتون من فوق) يمكنك حساب رباعي:

$$

$$q_ {v، \ varphi} = \ left [\ cos \ left (\ frac {\ varphi} {2} \ right) \ \ v_x \ sin \ left (\ frac {\ varphi} {2} \ right) \ \ v_y \ sin \ left (\ frac {\ varphi} {2} \ right) \ \ v_z \ sin \ left (\ frac {\ varphi} {2} \ right) \ right] \ quad (*)$$

ثم ، باستخدام الجيروسكوب فقط ، في كل تكرار للدورة ، سنحسب القيمة الحالية للرباعي وفقًا للتعبير:

$$

$$q_n ^ G = q_ {n-1} q_ {v، d \ varphi}$$

هنا $$$q_n ^ G$ - رباعي في وقت معين. يشير المؤشر G في الأعلى إلى أن هذه القيمة تشير إلى المقاس بالنسبة لقراءات الجيروسكوب ، أي السرعة الزاوية $$$q_ {n-1}$ - قيمة الرباعية في اللحظة السابقة ؛ $$$q_ {v، d \ varphi}$ –تغيير الموضع في خطوة قياس واحدة ، يمكننا أن نقول تغيير منفصل للموضع بزاوية $$$d \ varphi$ ل $$$dt$ هي فترة أخذ العينات التي يعبر عنها رباعي الدوران (*).

الخطوة التالية في الحساب هي العثور على مصفوفة الدوران بناءً على بيانات من زوج من مستشعرات مقياس التسارع والمغنطيسية. على وجه التحديد ، نعتبر متجه الجاذبية ومتجه الحث للمجال المغناطيسي للأرض ، كما هو مذكور أعلاه ، ثابتًا فيما يتعلق بالأرض و NSC المرتبط به. هنا الأطروحة هي: معرفة قيم الجاذبية والتحريض في أساس LSC و NSC ، يمكننا حساب مصفوفة الانتقال (الدوران) من NSC إلى LSC ورباعي الدوران في الفضاء .

دلالة بواسطة $$$\ vec {G}$ ناقلات الجاذبية الأولية المقيسة. يمكن أن تؤخذ على النحو التالي:

$$

$$\ vec {G} = {\ يسار [0 \ 0 \ 1 \ يمين]} ^ T$$

من خلال $$$\ vec {H}$ تشير إلى ناقلات الحث المغناطيسي الأولي المقيسة:

$$

$$\ vec {H} = {\ يسار [H_x \ H_y \ H_z \ right]} ^ T$$

مطلوب ناقل ثالث أيضا. $$$\ vec {K}$ الذي يرتبط بهذين. يتم الحصول عليها عن طريق الضرب ناقلات $$$\ vec {H}$ على $$$\ vec {G}$ :

$$

$$\ vec {K} = {\ left [K_x \ K_y \ K_z \ right]} ^ T = \ vec {H} \ times \ vec {G} = {\ left [H_y \ -H_x \ 0 \ right]} ^ T$$

الآن يتم تشكيل المصفوفة $$$M_0$ الذي يميز الموقف الأولي ، أي NSC ، منذ ذلك الحين ، يتزامن LSC مع NSC. يتم الحصول على المصفوفة من مكونات المتجهات $$$\ vec {H}$ ، $$$\ vec {G}$ و $$$\ vec {K}$ :

$$

$$M_0 = \ left [\ vec {H} \ \ vec {G} \ \ vec {K} \ right] = \ left [\ start {array} {cccc} H_x & 0 & H_y \\ H_y & 0 & -H_x \\ H_z & 1 & 0 \ end { المصفوفة} \ right]$$

وبالمثل ، ولكن بالفعل عند كل تكرار للحلقة ، يتم إنشاء مصفوفة مماثلة $$$M '= \ left [\ vec {h} \ \ vec {g} \ \ vec {k} \ right]$ أين $$$\ vec {h}$ هو ناقل الحث المغناطيسي المعياري الحالي ، $$$\ vec {g}$ هو ناقل الجاذبية المقيس الحالي ، $$$\ vec {k} = \ vec {h} \ times \ vec {g}$ . تصف هذه المصفوفة موقف LSC ، لأنه تُعرف هذه المتجهات في نظام إحداثيات المستشعرات ، الذي يتزامن مع LSC. بعد ذلك ، بمعرفة كلتا المصفوفتين ، يمكننا كتابة المعادلة التالية:

$$

$$E'M '= E_0M_0$$

يربط مصفوفتين تم العثور عليهما في ظروف مختلفة. نظرا لتعبير $$$E '= CE_0$ وما الأساس $$$E_0$ هل مصفوفة الهوية نحصل على:

$$

$$CM '= M_0$$

من هنا نعبر عن مصفوفة الانتقال $$$C$ :

$$

$$C = {\ left (M_0 ^ {- 1} \ right)} ^ TM '^ T$$

يتم احتساب العامل الأول ، كما يمكنك فهمه ، مرة واحدة فقط في بداية الخوارزمية ، ولا يتطلب إعادة العد في هذه العملية. يتشكل العامل الثاني بسهولة تامة ولا يتم إجباره عند كل تكرار للدورة.

بعد ذلك ، عندما يتم العثور على مصفوفة الانتقال ، نقوم بتحويلها إلى رباعي $$$q_n ^ A$ (خوارزمية التحويل من مصفوفة إلى رباعي هو أمر عام ولن أعطيه هنا).

نتيجة لذلك ، نحن نعرف وجود رباعتين موجودتين بشكل مستقل عن بعضهما البعض. وللجمع بين النتائج ، قمت بتطبيق مرشح مكمل بسيط بمعامل $$$F$ والتي تؤخذ من النطاق من 0 إلى 1:

$$

$$q_n = Fq_n ^ G + \ left (1-F \ right) q_n ^ A$$

ونتيجة لذلك ، نحصل على رباعي ، يحتوي على معلومات محدثة حول الموضع في الفضاء مع وحدة SINS.

ذهبت الدراجة ... عملت الخوارزمية ، لكنها في بعض الحالات تصرفت بشكل غير لائق إلى حد ما ، وهو ما لم يتدخل من حيث المبدأ ، لكنه لم يعط سببًا للتفكير بشكل إيجابي في ذلك. أنا راضٍ عن اهتمامي الرياضي ، والآن يمكنك اللجوء إلى الحلول الجاهزة بشكل أفضل. ثم عدت مرة أخرى إلى مقال سيباستيان مجويك وقررت استخدام خوارزميته ، لحسن الحظ ، أن هذا الشخص الرائع نشر جميع أكواد المصدر على موقع المشروع . يحتوي الأرشيف على رموز مصدر بلغات مختلفة ، بما في ذلك لغة Matlab. أثرت هذه الحقيقة على قراري بالتخلي عن فكرة إجراء جميع الحسابات على وحدة التحكم الدقيقة (خاصة أنها 8 بت) وكتابة البرنامج بالفعل على الكمبيوتر في بيئة Matlab. يتم استخدام وحدة التحكم الدقيقة فقط لاستجواب المستشعرات وإرسال البيانات إلى جهاز الكمبيوتر (وهو وضع مشابه مع المعالج). في هذه الحالة ، يستند رمز البرنامج الرئيسي الذي يخضع للتغييرات وتصحيح الأخطاء في بيئة Matlab ، وهو أمر مريح للغاية في هذه العملية.

حسنًا ، التوجيه الذي حصلنا عليه من الرباعية. ما هي الخطوة التالية وفقًا للخطة؟ ثم يتبع الإحداثيات الخطية للكائن حسب مقياس التسارع. حسنًا ، من الأفضل هنا أن نذكر ببساطة أنه من المستحيل تحديد الإحداثيات باستخدام مقياس التسارع بالدقة اللازمة. حتى على الأقل العثور على تغيير في الموقف الذي سيكون كافيا! بالطبع ، كانت هناك محاولات لحل هذه المشكلة ، ولكن في الوقت الحقيقي لم يكن من الممكن العثور على الإحداثيات. لماذا؟ لأن التكامل المزدوج المنفصل لقراءات أجهزة الاستشعار الصاخبة أدى فقط إلى التحليق في الستراتوسفير ، وبسرعة محمومة ، ولكن ليس إلى نتيجة إيجابية. لذلك ، قطعت الخوارزمية المشار إليها في بداية الفقرة حتى تم العثور على الاتجاه ، وتوقفت عند هذا الحد.

3. كل شيء آخر

لذا ، وصلت إلى المرحلة النهائية من التصميم ، بعد أن لعبت بما يكفي مع المعالج ومستشعر IMU الملفوف. أثناء العمل على الخطوتين السابقتين ، كان لدي بالفعل فكرة واضحة عن كيفية عمل كل شيء وبأي خوارزمية. لذلك تعاملت مع هذه المرحلة بسرعة كافية. نظرًا لأن اتجاه راحة اليد فقط معروف ، فإننا نعمل مباشرة مع هيئة العمل ، وهو مطلوب للتوجيه وفقًا لذلك. يمكن أن يأخذ RO أي اتجاه ، إذا لم ينتهك منطقة العمل (تدوير جميع 360 لا يعمل).

في البند المتعلق بتطوير المناور ، تم تعيين ناقل أمر الشراء يدويًا ، وبعد ذلك تم العثور على زوايا دوران محركات الأقراص. لذلك ، يجب تحديد هذا الناقل بناء على اتجاه راحة اليد. يمكن التعبير عن التوجيه كأساس $$$E '$ إيجاده عن طريق تحويل الرباعي إلى مصفوفة. يتكون الأساس من متجهات أعمدة من مقوماتها ، وبالتالي نحصل على ثلاثة متجهات $$$\ vec {x} '$ ، $$$\ vec {y} '$ و $$$\ vec {z} '$ . سيكون من الملائم أخذ المتجه كالتوجيه $$$\ vec {x} '$ ، منذ أن افترضت مثل هذا الموقف الأولي للمعالج ، عندما تكون جميع الروابط و PO في مستوى XZ لنظام الإحداثيات الأساسية ، و PO في الوضع الأفقي في تلك اللحظة ، أي ناقلات $$$\ vec {v_0}$ في البداية ، يتم محاذاته مع المحور X لـ BSK و NSC (نضع الموضع الأولي لوحدة SINS بحيث يتزامن NSC مع BSK الخاص بالمناور). في هذه الحالة ، العمود الأول من المصفوفة $$$E '$ يساوي متجه $$$\ vec {v_0}$ . ثم نقوم بتطبيعها على طول أمر الشراء ونحصل على المتجه المطلوب بالنسبة لنظام الإحداثيات الأساسي للمعالج. ثم نتبع تسلسل حساب الإحداثيات المعممة من الصفحة 1.

تجدر الإشارة إلى أن المناور ، عند تغيير اتجاه RO ، قادر على التحرك في وضعين: الأول - عندما تكون نقطة الشفة ثابتة ، والثاني - عندما تكون نقطة نهاية أمر الشراء ثابتة ، ولكن يتم ملاحظة اتجاهها. الوضع الثاني أكثر إثارة للاهتمام لأنه حتى في غياب الحركة الخطية ، لا تزال جميع محاور الدوران متداخلة لتحريك نقطة الحافة ، مع ملاحظة اتجاه أمر الشراء. ومع ذلك ، يحدث الانتقال من الوضع الأول إلى الثاني مع إضافة عملية واحدة فقط لطرح المتجهات للعثور على المتجه $$$\ vec {r}$ (انظر الفقرة 1).

تمت برمجة جميع العمليات المذكورة أعلاه أيضًا في بيئة Matlab. بشكل عام ، هيكل البرنامج على النحو التالي:

1. المعايرة عند بدء التشغيل. قمنا بتعيين المزرعة بأكملها إلى وضعها الأصلي وبدون تجرؤ على اللمس ، قم بمعايرة وحدة SINS لكمية معينة من البيانات الخام منها. المعايرة ضرورية ، لأنك تحتاج إلى إزالة الإزاحة الأولية التي أنتجها الفلتر (لم أفهم السبب ، وعملت على ما يرام).
2. بداية النص. نقوم بتهيئة جميع المكتبات والمتغيرات ، ونقوم بتعيين الموضع الأولي لشفة أو نقطة نهاية أمر الشراء.
3. بداية الدورة. في كل تكرار ، نستجوب أجهزة الاستشعار ، ونعثر على الرباعية ، ونترجمها إلى مصفوفة ، وهي الأساس $$$E '$ ، هو الأساس الذي يقع فيه RO. يؤخذ العمود الأول كتوجيه لأمر الشراء ونجد جميع الإحداثيات المعممة باستخدام الاعتبارات الرياضية من القسم 1.
4. بمعرفة الإحداثيات المعممة في اللحظة الأخيرة من الوقت وفي الوقت الحاضر ، نحسب السرعة الزاوية لتدوير المحاور.
5. نرسل حزمة بيانات إلى وحدة التحكم الدقيقة في المعالج.

اتضح أنه خرقاء بالطبع ، ولكن إذا ألقيت نظرة فاحصة ، يمكنك رؤية نتيجة إيجابية للدراسة. هذا العمل ، بالطبع ، لا يدعي أنه تم الانتهاء منه ويتطلب الكثير من الجهد لتحسينه ، ولكن فقط إذا كان من الممكن استخدامه. ولكن لم أجد حتى الآن تطبيقًا محددًا ... هل يمكن لأحد أن يخبرني؟