
مرحبا يا هبر! في هذه المقالة سوف أتحدث عن إنشاء نموذج رياضي لخط أنابيب طويل لبرنامج محاكاة CAE في Modelica. ستكون مسألة حساب عمليات الموجة (نبضات الضغط ، المطرقة المائية ، إلخ) في خط هيدروليكي باستخدام طريقة الخصائص. على الرغم من حقيقة أن هذه الطريقة قديمة جدًا ، إلا أنه لا توجد معلومات كافية في RuNet حول تطبيقها لحل المشكلات التطبيقية.
تحت القطع ، سأحاول أن أشرح لماذا من الضروري أن تأخذ في الاعتبار عمليات الموجة في خطوط الأنابيب ، لتسليط الضوء على المشاكل التي واجهتها أثناء البرمجة وفي النهاية سأقدم مقارنة لعملية نبضات الضغط أثناء تشغيل مضخة المياه ذات الضغط العالي بثلاثة مكابس على خط أنابيب طويل بسيط في النموذج وعلى حامل URACA في ألمانيا.
مقدمة
في الممارسة الهندسية ، كقاعدة عامة ، يتم إيلاء القليل من الاهتمام لعمليات الموجات في خطوط الأنابيب. المثال الأكثر شهرة ، عندما تفسد عمليات الموجة حياة المهندس ، هي مطرقة مائية:
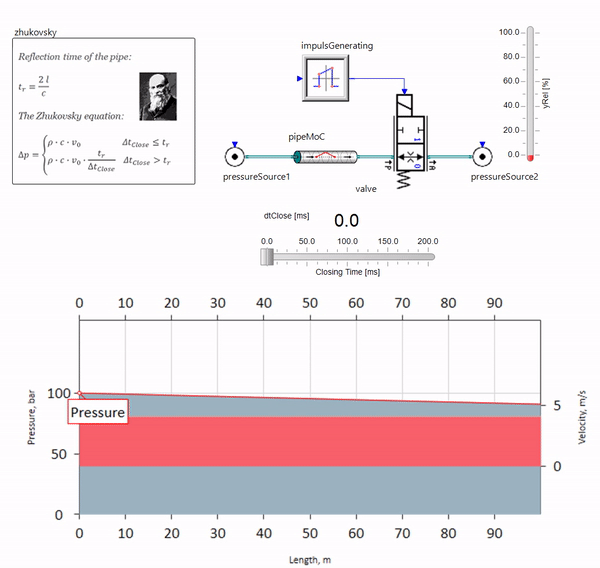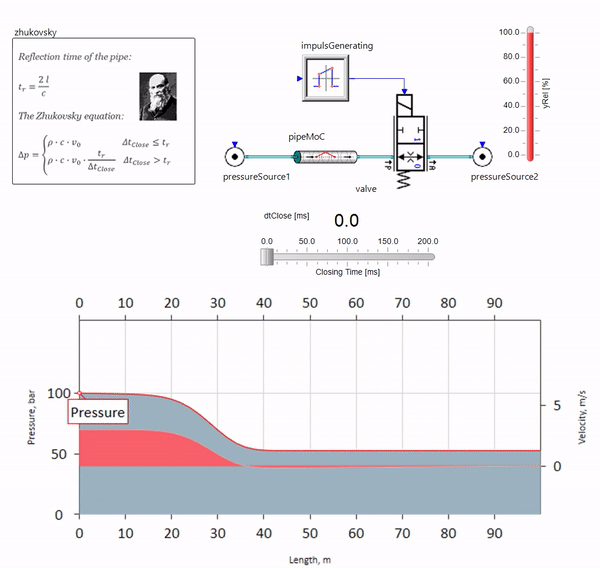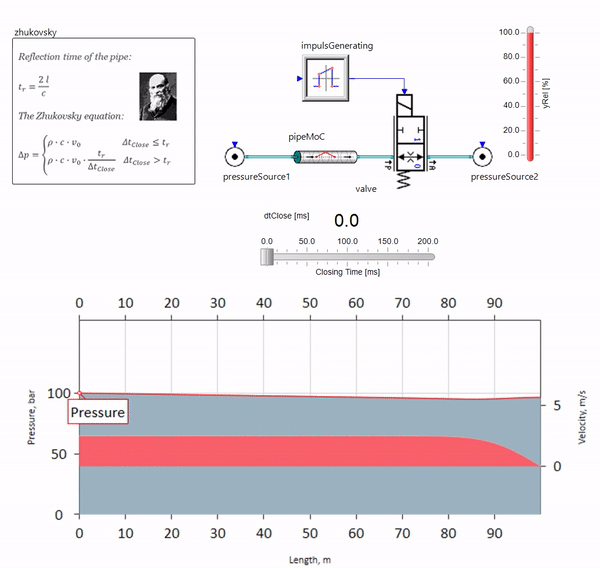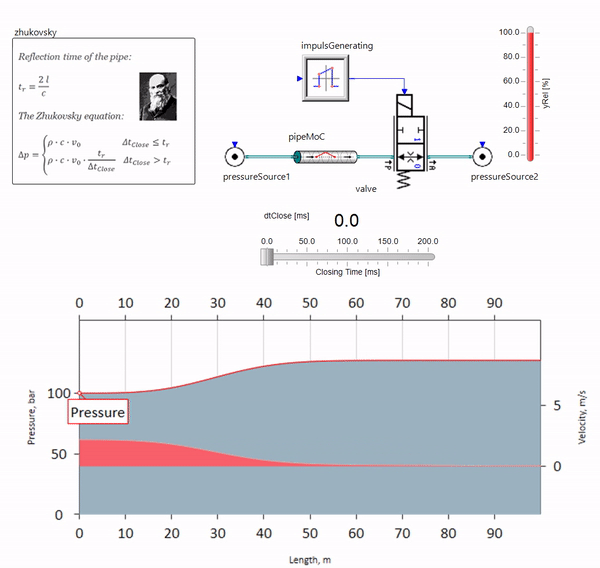
عندما يغلق الصمام بسرعة في نهاية خط الأنابيب ، في اتجاه المصب ، تحدث موجة ضغط تتحرك في اتجاه التيار عند سرعة الصوت المحلية (بالنسبة للماء ، حوالي 1500 متر / ثانية) ، تنعكس من مصدر ضغط ثابت ، وتعود إلى الصمام وتنعكس من لها هذه المرة بعلامة سلبية. تتكرر هذه العملية حتى يتم إنفاق كل الطاقة على الاحتكاك ، وحتى ذلك الحين يتعرض الصمام وخط الأنابيب بالكامل لأحمال الصدمة ، التي يعتمد اتساعها وتواترها على طول خط الأنابيب والسرعة الأولية لتدفق السوائل.
تم وصف التدفق المائي بالدقة اللازمة لحل المشكلات العملية في نهاية القرن التاسع عشر من قبل نيكولاي جوكوفسكي ، وبالتالي حل مشكلة الحوادث في إمدادات المياه في موسكو. منذ ذلك الحين ، تسمى صيغة حساب قفزة الضغط عند إغلاق الصمام بسرعة
صيغة Zhukovsky في جميع أنحاء العالم:
تتجلى مطرقة المياه عمليًا ، كقاعدة عامة ، مع أطوال خطوط الأنابيب من مائة متر. في الأطوال أدناه ، من الصعب بالفعل العثور على معدات هيدروليكية يمكن أن تغلق بشكل أسرع من موجة الضغط التي تمر من الصمام والظهر (حالة حدوث المطرقة المائية). ومع ذلك ، حتى خطوط الأنابيب القصيرة نسبيًا يمكن أن تدمر حياة المهندسين إذا كان للنظام مصدر نبضات تدفق (على سبيل المثال ، مضخة حجمية مع عدد محدود من الغطاسات).
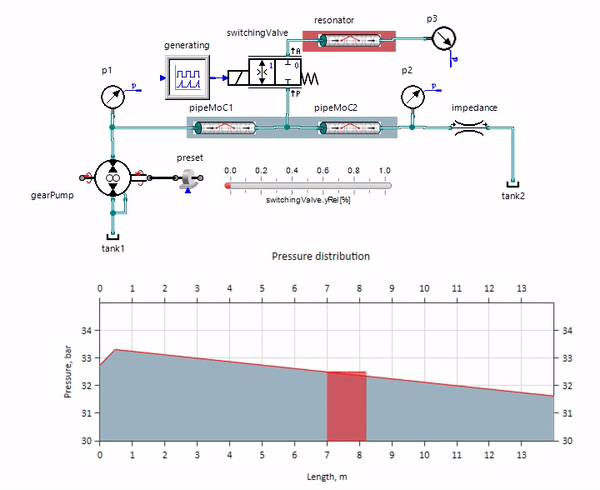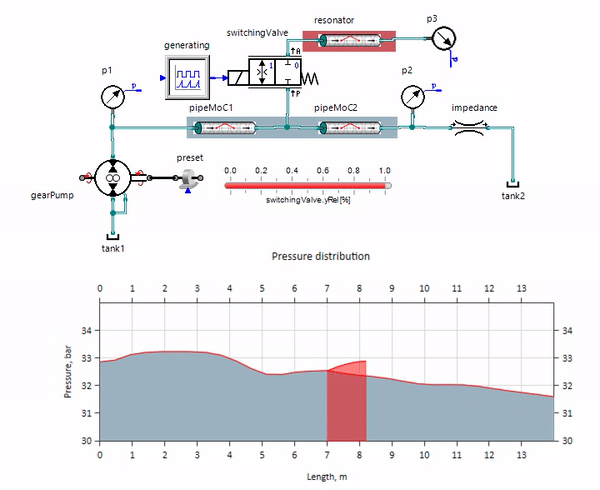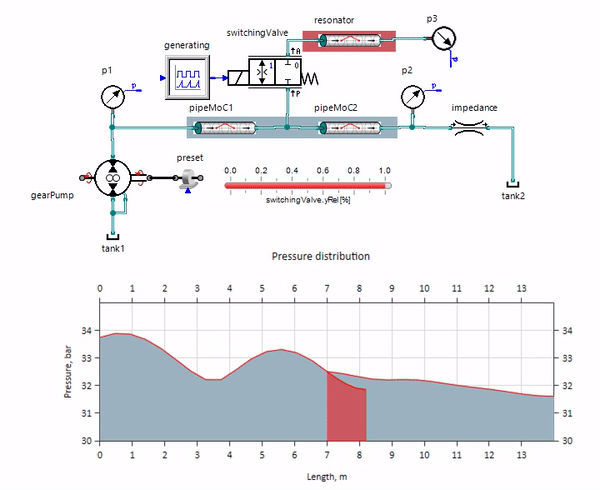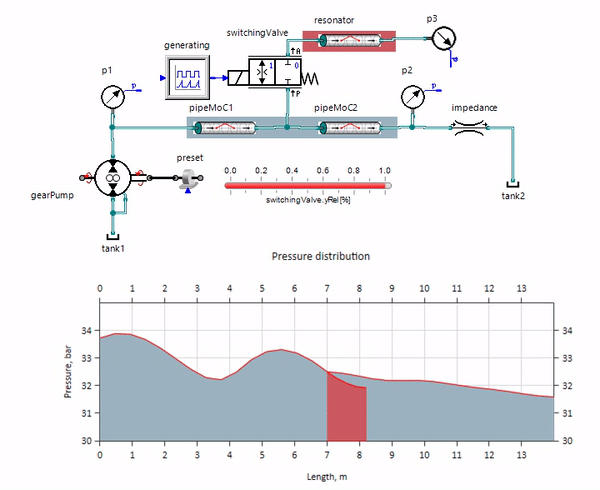
يظهر gif التأثير المفيد لقطعة من خط الأنابيب يزيد قليلاً عن متر واحد. طوله يساوي ربع الطول الموجي للضغط ، لذلك عند توصيله بخط الأنابيب الرئيسي ، فإن ما يسمى موجة واقفة ، والتي تصطدم بمنبض النبضات في الطور المضاد وتثبطها بهذه الطريقة (وهذا ما يسمى بخافت نبضة ربع الموجة). من الواضح أنه مع وجود مزيج مؤسف من الظروف ، قد يكون التأثير عكس ذلك.
في ممارستي ، حاولت لفترة طويلة أن أتجاهل عمليات الموجة ، لأن تطلبت حساباتهم فهماً أعمق لطرق ماتان والعددية ، التي تعاملت معها طوال دراستي بإهمال متسامح. ولكن عندما رأيت ذات يوم بأم عيني أن النصيحة القياسية (لوضع HPP ، المجمع الهيدروليكي في كل مكان لتنظيم احتياطي في مدخل المضخة) لا يساعد إما في التخلص من النبضات على المقعد ، ولا ، بالإضافة إلى ذلك ، جعلهم أقرب إلى فهم العمليات ، كان علي أن أعمق في حصيرة . خاصة بالنسبة للعار ، بدأ مشرف البحث بالفعل في كتابة نموذج خط أنابيب في C ++ بالنسبة لي.
1. نموذج أحادي البعد للخط الهيدروليكي في المعلمات الموزعة
المشكلة الرئيسية التي تجعل النماذج التقليدية أحادية البعد الموصوفة بواسطة المعادلات التفاضلية العادية تتجاوز منطقة الراحة هي أن أبسط خط أنابيب ، حتى مع أكثر الافتراضات فظاعة (مليء بالكامل بالسائل ، له طول مستعرض مستقر ، يتم حساب متوسط سرعة المائع عبر المقطع العرضي ، ولا يتم إجراء عمليات نقل الحرارة يتم اعتباره) موصوفًا بواسطة معادلات تفاضلية في المعلمات الموزعة (معادلات أويلر ، مع مراعاة فقط قوة الكتلة والاحتكاك على الجانب الأيمن من الثانية avneniya):
أين - الكثافة - السرعة - الضغط - خسائر الاحتكاك ، - انخفاض الضغط الناجم عن قوة الجاذبية.على سبيل المثال الاندماج الآن لا تحتاج فقط في الوقت المناسب
ولكن أيضًا في إحداثيات مكانية
.
في حالة السوائل ، يمكنك تبسيط حياتك أكثر قليلاً إذا قمت بإعادة كتابة المعادلات من المتغيرات المحافظة إلى المتغيرات البدائية (السرعة والضغط):
أين - سرعة الصوت.الآن ، إذا قبلنا أن سرعة الصوت أكبر بكثير من سرعة حركة السوائل
(وهذا صحيح في حالة عدم وجود التجويف) ، ستصبح المعادلات أبسط قليلاً:
لحل هذه المعادلات ، بطريقة أو بأخرى ، تخلص من التمايز في الإحداثيات المكانية
. يمكن القيام بذلك مباشرة إذا استبدلت التفاضل المكاني بمخطط الفروق المحدودة ، وفي حالة الوقت ، انتقل فقط إلى التفاضل الكامل ، قائلًا أنه داخل نفس الخلية ، لا تعتمد معلمات الحالة على الإحداثيات:
الآن يمكن حل هذه المعادلات كمعادلات تفاضلية عادية ، وتقسيم طول الأنبوب إلى العديد من الأحجام المحدودة. لذلك
يتم ذلك ، على سبيل المثال ، في حزمة Simscape ، في MATLAB Simulink ، وبالتالي تم حل المشكلة حتى وقت قريب في
SimulationX .
شيء ما بهذه الطريقة ، بالطبع ، يمكن حسابه ، لكن التقلبات العددية التي تنشأ في هذه الحالة تعوق بشكل كبير:
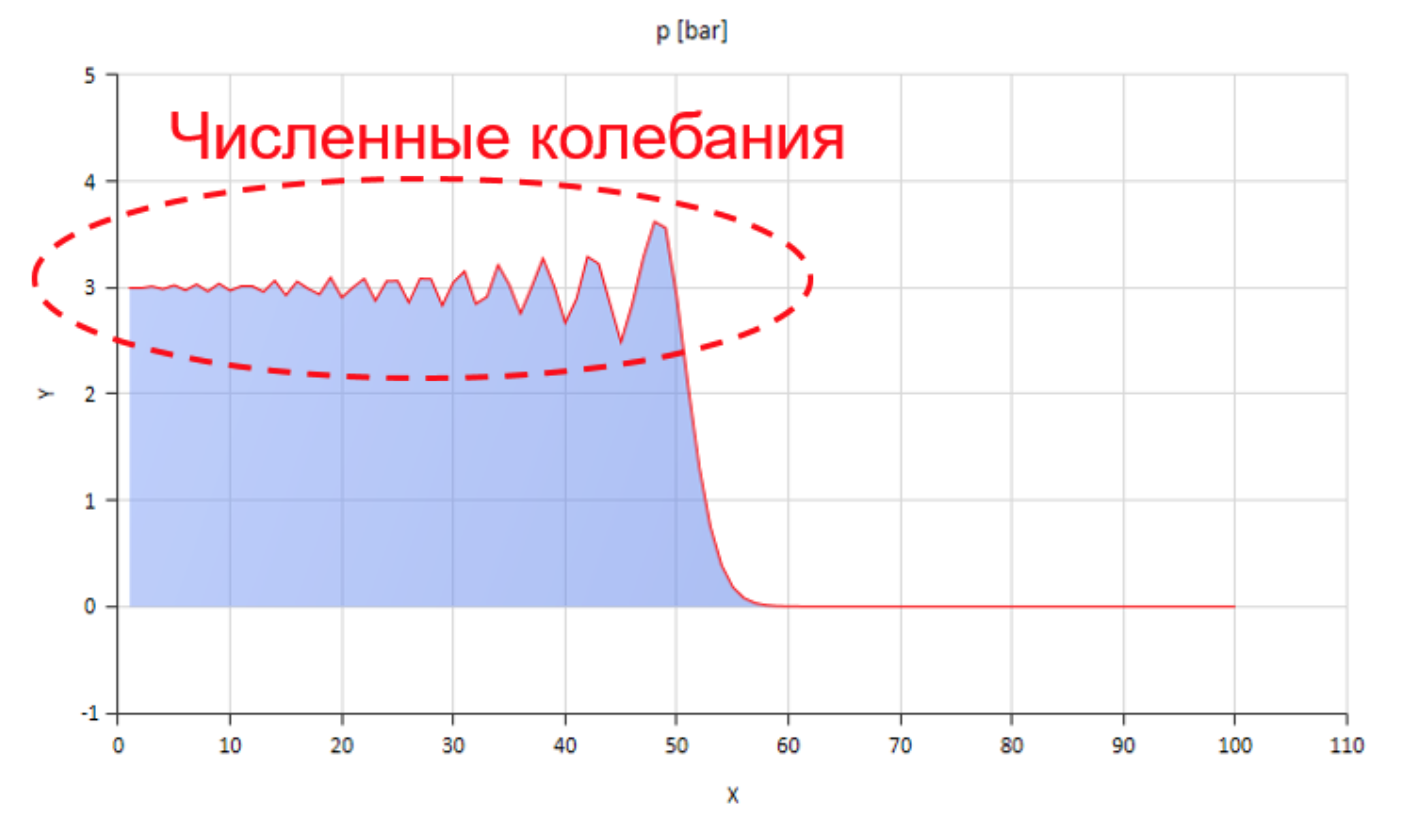 يوضح الشكل مقدمة موجة الضغط تتحرك من اليسار إلى اليمين.
يوضح الشكل مقدمة موجة الضغط تتحرك من اليسار إلى اليمين.يمكنك التعامل مع هذه التذبذبات ، على سبيل المثال ، إدخال الانتشار العددي ، ولكن بعد ذلك يتم تشويه سرعة انتشار الموجة بشكل كبير. يمكنك زيادة الاحتكاك (خاصة المساعدة في زيادة المكون غير الثابت) ، ولكن بعد ذلك يتوقف النموذج عن عكس الجوهر المادي.
من الأفضل استخدام طريقة مختلفة لتحويل المعادلات في المعلمات الموزعة إلى معادلات تفاضلية عادية ، على سبيل المثال ، طريقة الخصائص.
2. طريقة توصيف
توصي
ويكيبيديا بـ "طريقة الخصائص" توصي بما يلي:
... لإيجاد الخصائص التي تتحول من خلالها المعادلة التفاضلية الجزئية إلى معادلة تفاضلية عادية. بمجرد العثور على المعادلات التفاضلية العادية ، يمكن حلها على طول الخصائص ويمكن تحويل الحل الموجود إلى حل المعادلة التفاضلية الجزئية الأصلية.
إنه مثل حجر فيلسوف ، ولكن بدلاً من تحويل المعادن إلى ذهب ، نحول المعادلات التفاضلية الجزئية إلى معادلات عادية ، والعكس صحيح. السؤال الذي يطرح نفسه: "كيفية تطبيق هذا في الممارسة العملية؟" ، ويفضل أن يكون أكثر فعالية من الكيميائيين في العصور الوسطى ...
بادئ ذي بدء ، سوف نفهم بيان المشكلة. في اللحظة الأولى من الوقت ، لدينا نوع من توزيع الضغوط والسرعات على طول الأنبوب. أولاً ، نكسر الأنبوب إلى عدد محدود من العناصر ونعين قيمة ضغط لكل وجه
والسرعة
.
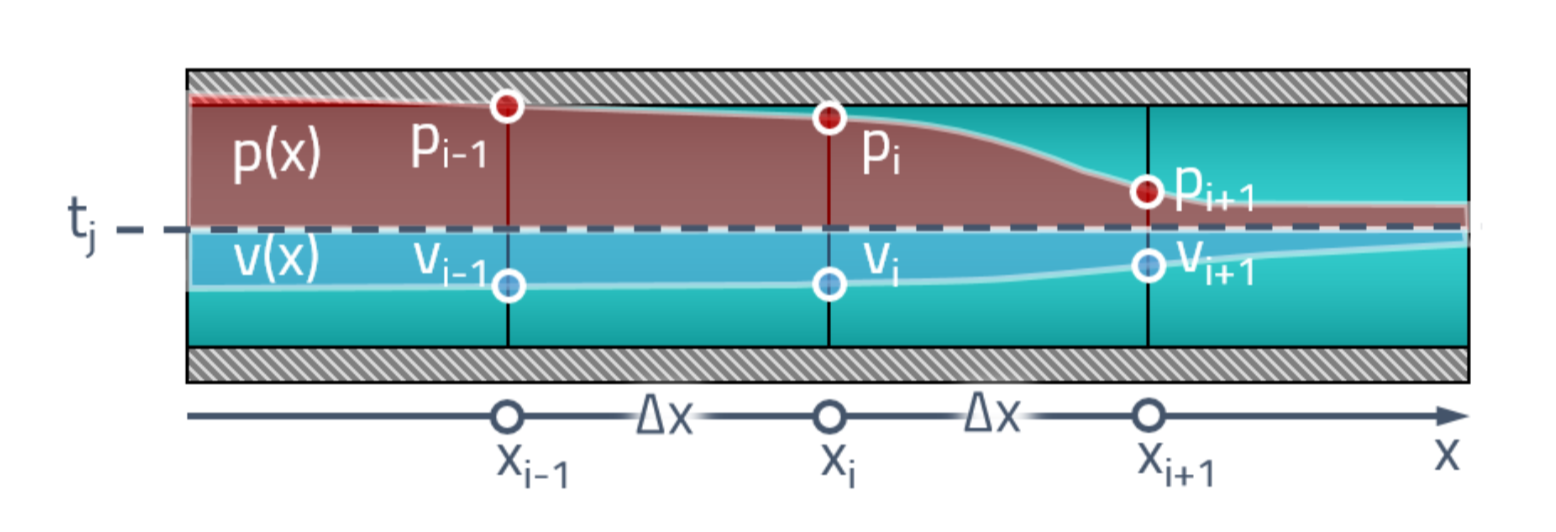
نحن مهتمون بكيفية تغير القيم في هذه النقاط بمرور الوقت
. تقديم سريع إلى الزمكان ووضع حالة الأنبوب في المستقبل فوق الحالة الأولية:

هنا يأتي دور الخصائص "السحرية"! تفسير الفلاحين العاملين هو أن جميع التغييرات في الأنبوب تحدث بسرعة الصوت. الضغط والسرعة عند النقطة الزمنية الحالية
تعتمد على الضغط والسرعة عند تلك النقاط في الأنبوب حيث كانت الموجة الصوتية (ستفعل)
قبل ثوان. هذا موضح على النحو التالي:

يتم رسم خطين متناظرين من أي نقطة ، يتم تحديد ميلها من خلال سرعة الصوت. هذه هي الخصائص التي تتحول من خلالها المعادلات التفاضلية الجزئية إلى معادلات تفاضلية عادية. إذا قمنا بتسمية النقاط التي تتقاطع عندها الخصائص مع حالة الأنبوب في الماضي
و
، تتم كتابة المعادلات على النحو التالي:
يمكن الحصول على قيم الضغوط والسرعات عند هذه النقاط من خلال الاستكمال الخطي بين قيم معلمات الحالة على الشبكة:

من المهم مراعاة أن هذه النقاط يجب أن تكون دائمًا داخل الخلايا المجاورة! لهذا ، يجب أن تستوفي الخطوة الزمنية معيار Courant - Friedrichs - Levy (CFL):
الآن ، يمكن تطبيق أبسط مخطط فرق على الأقل على هذه المعادلات:
في النظام الناتج من معادلتين ، مجهولان: الضغط
والسرعة
. يمكنك حلها عدديًا ، ولكن لا توجد مشكلة معينة للحصول على حل تحليلي. ثم ، إذا قبلنا ثبات سرعة الصوت ، نحصل على مخطط فرق واضح تمامًا.
للتوحيد ، سأقدم رسومًا متحركة لطريقة الخصائص:
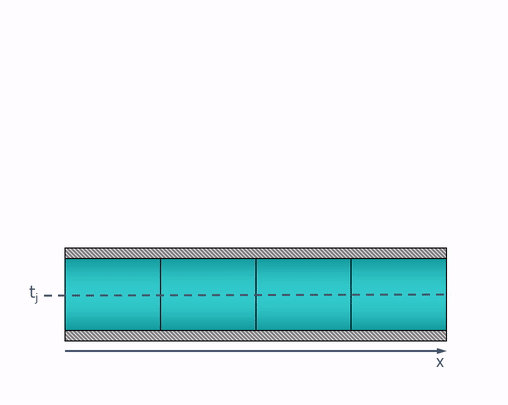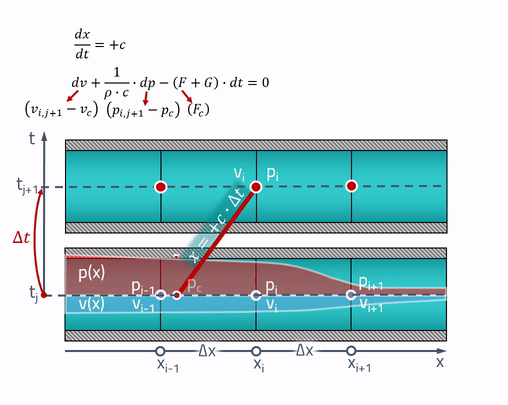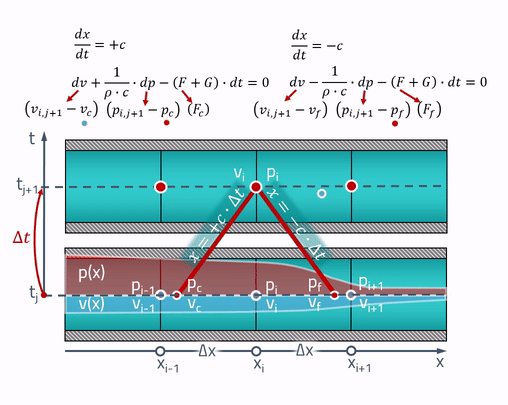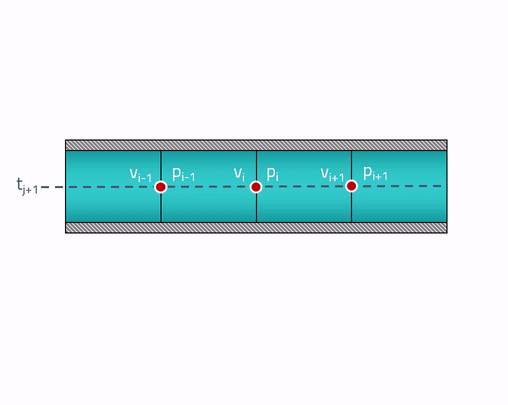
في الحقيقة ...... تعتمد سرعة الصوت على ضغط السائل. في هذه الحالة ، لن تكون الخصائص ، بشكل دقيق ، خطوطًا مستقيمة بعد الآن ، ولكن من أجل العثور على الضغط ، ستحتاج إلى معرفة سرعة الصوت ، والتي تعتمد على هذا الضغط. على سبيل المثال ستكون الدائرة ضمنية بالفعل.
عند إنشاء النموذج ، قبلت الافتراض بأن سرعة الصوت تتغير قليلاً فقط من خطوة إلى خطوة. بالنسبة للسوائل ، هذا صحيح في حالة انخفاض محتوى الغاز وغياب التجويف. للتأكد من النتيجة ، يُفضل استخدام النموذج عند ضغط 10 بار أو أكثر.
3. التجربة
لقد أتيحت لي الفرصة أخيرًا لتذكير النموذج بالفعل عندما بدأت العمل في
ESI ITI GmbH في درسدن. مرة ، تلقيت تذكرة في مكتب المساعدة ، حيث اشتكى مهندسو
URACA من أنهم لم يتمكنوا من تحقيق التقارب مع التجربة باستخدام الأنابيب "القديمة".
إنهم يصنعون مضخات غطاس المياه ذات الضغط العالي ، مثل "كارشر" الضخم ، ويودون أن يكونوا قادرين على التنبؤ بآثار الرنين المحتملة بسبب تضمين عمليات الموجة في خط الأنابيب. تكمن المشكلة في أن هذه المضخات ، كقاعدة عامة ، تحتوي على عدد قليل جدًا من الغطاسات وتعمل بسرعات منخفضة (250-500 دورة في الدقيقة):

ونتيجة لذلك ، وأيضًا بسبب تأثير انضغاط السائل ، يكون الإخراج متدفقًا للغاية:

تجعل الثغرات والغير خطية من الصعب تحليل النموذج في مجال التردد وتحليله ، وحسابات CFD لمثل هذه المهمة يتم إطلاقها من مدفع على العصافير. بالإضافة إلى ذلك ، لديهم بالفعل نماذج في SimulationX ، حيث أخذوا في الاعتبار ديناميكيات الجزء الميكانيكي من المضخة ، ومرونة الإطار ، وخصائص المحرك الكهربائي ، لذلك سيكون من المثير للاهتمام أن نرى كيف يؤثر خط الأنابيب على ذلك.
تخطيط مقاعد البدلاء اختبار بسيط للغاية:
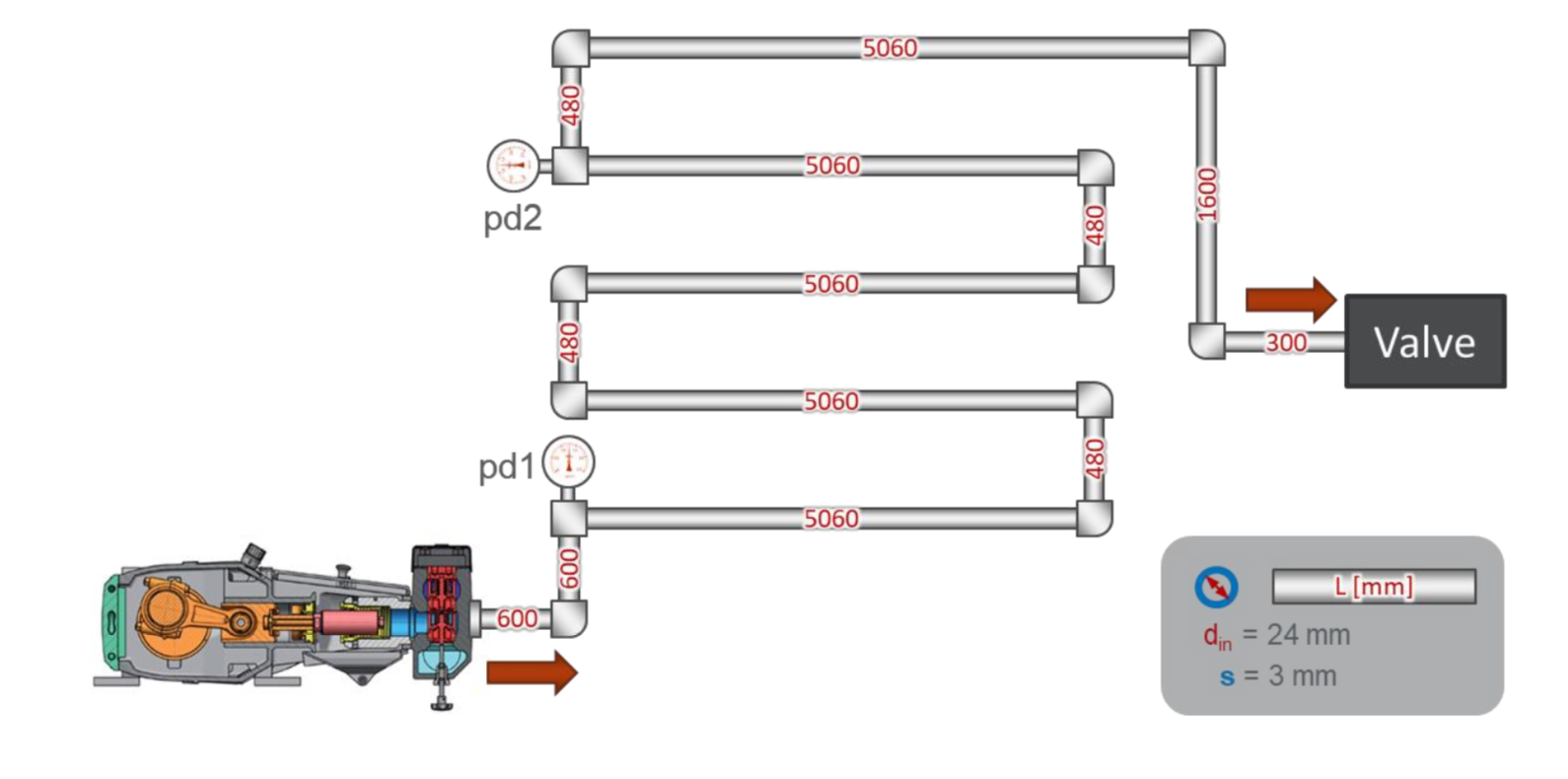
يوجد خط أنابيب بسيط بطول إجمالي حوالي 30 مترًا. في بداية خط الأنابيب ، يتم تركيب جهاز استشعار الضغط pd1 ، على مسافة 22 مترًا منه - جهاز استشعار الضغط pd2. في نهاية خط الأنابيب يوجد صمام يضبط الضغط في النظام.
اقترحت اختبار الإصدار التجريبي من نموذجي ، نتيجة بناء هذا النموذج في SimulationX:
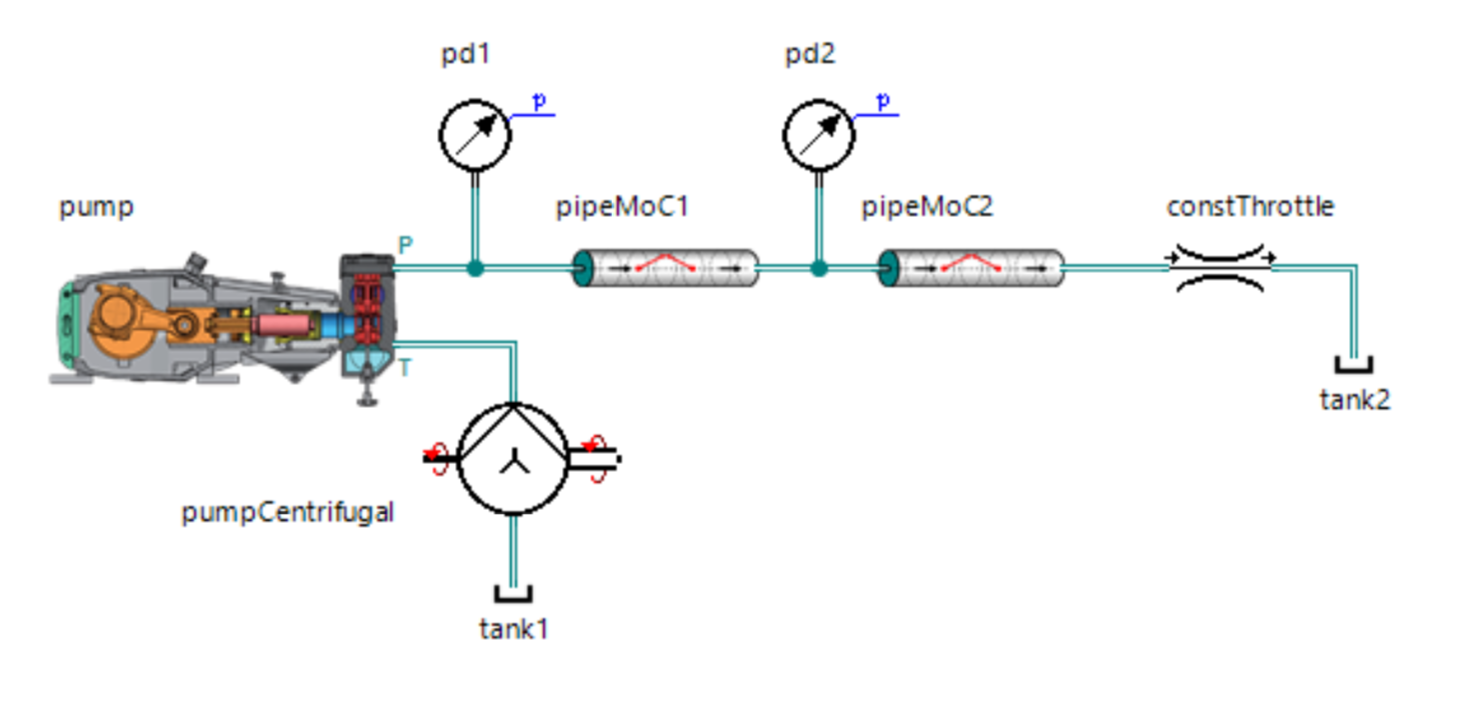
حتى النتائج فاجأتني:
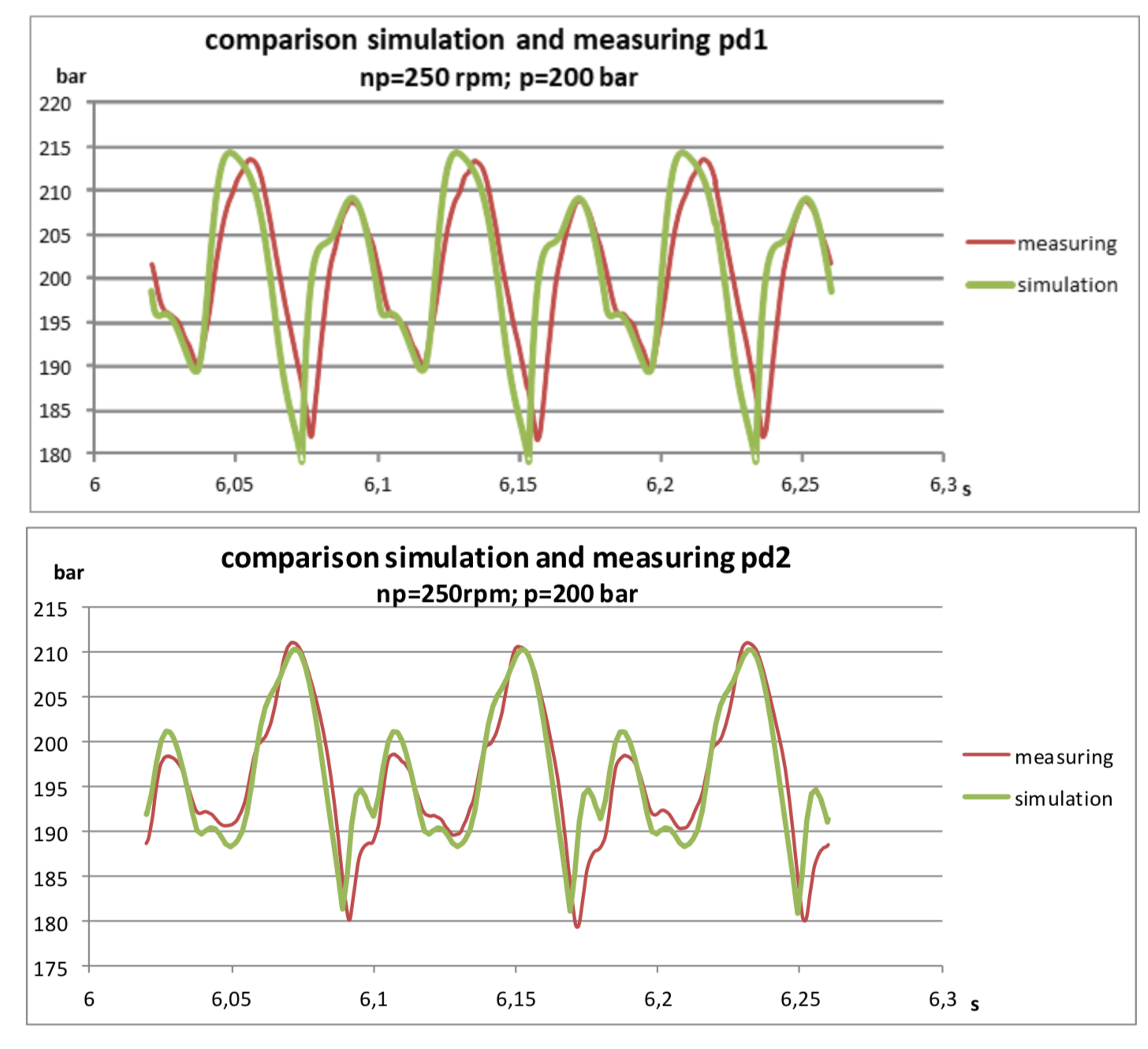
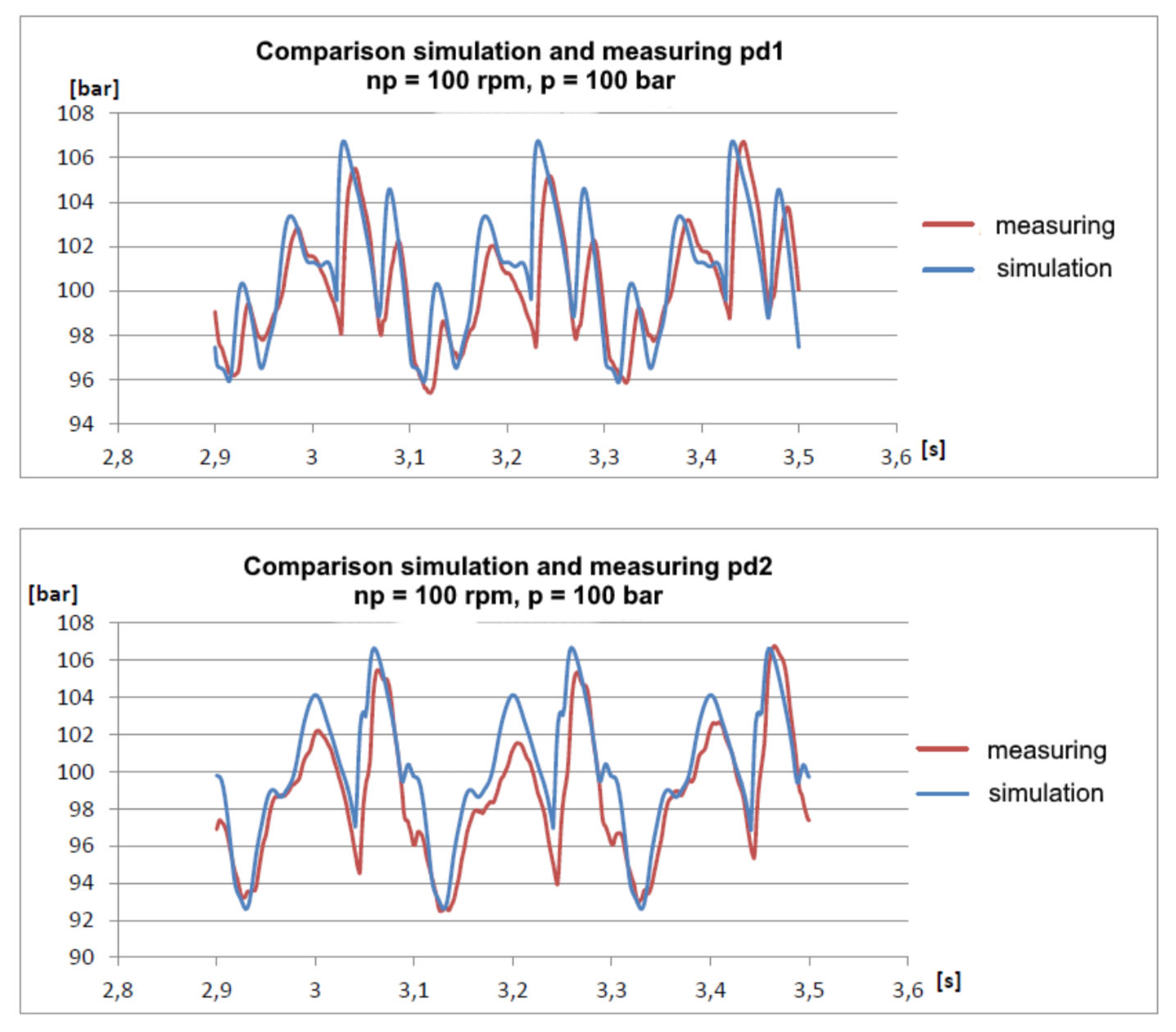
يمكن ملاحظة أن النموذج مبلل قليلاً ، وهو أمر مفهوم بشرط ألا يأخذ في الاعتبار المقاومة الهيدروليكية. ومع ذلك ، فإن التوافقيات الأساسية جيدة جدًا في الصدفة وتجعل من الممكن التنبؤ بسعات الضغط بدقة جيدة إلى حد ما.
سمحت لي هذه التجربة بإطلاق نموذج جديد سريعًا للخط الهيدروليكي في إصدار SimulationX ، وانغمست في هذا الموضوع ولم ألاحظ كيف ، إلى جانب الطالب المتدرب ، رأيت أيضًا نموذج الخط الهوائي ، حيث كان كل شيء أكثر إثارة للاهتمام. هناك ، اضطررت إلى استخدام طريقة تعتمد على طريقة Godunov ، والتي تعتمد بدورها على حل مشكلة Riemann المتمثلة في انحلال الانقطاع التعسفي ، حسنًا ، حول هذا بالفعل بطريقة أخرى في وقت آخر ...
الأدب
- في الأدب المحلي ، يتم وصف طريقة خصائص التطبيقات الهندسية بشكل أفضل في كتاب "الميكانيكا المائية" ، D. N. Popov ، S. S. Panaiotti ، M. V. ريابينين.
- في منشوره
محاكاة خطوط الأنابيب بطريقة الخصائص لحساب نبض الضغط لمضخة غاطس الماء ذات الضغط العالي"الدكتور إنغ (روس) مكسيم أندريف ، دبلوم إنغ. Uwe Grätz و Dipl.-Ing. (FH) Achim Lamparter ”، المؤتمر الدولي الحادي عشر لطاقة السوائل ، 11. IFK ، 19-21 مارس 2018 ، آخن ، ألمانيا ، يرجى الاطلاع على النص في PM
لقد درست بمزيد من التفصيل مشاكل اقتران طريقة الخصائص و حلالا ODE. - من لديه إمكانية الوصول إلى المكتبات الألمانية ، أفضل نظرة عامة على طرق حل المعادلات الزائدية المطبقة على الخطوط الهيدروليكية التي التقيت بها موجودة في الأطروحة التالية: Beck، M.، Modellierung und Simulation der Wellenbewegung in kavitierenden Hydraulikleitungen، Univ. شتوتجارت ، ألمانيا ، 2003.
- كلاسيكيات نوع المعادلات الزائدية بشكل عام: Randall J.Leveque، Finite Volume Methods for Hyperbolic Problems ، Cambridge University Press ، Cambridge ، United Kingdom ، 2002.