🍤 🚣🏼 🕤 البرمجة الديناميكية في مشاكل الأولمبياد 🤺 🔃 👨🏾‍🤝‍👨🏽

مرحبًا

لقد قمت مؤخرًا بحل المشاكل من أرشيف Timus Online Judge ووجدت قسمًا يسمى مهام البرمجة الديناميكية . هذا النوع من المهام له أهمية خاصة بالنسبة لي ، لأنه غالبًا ما يضمن هذا النهج سرعة وأناقة الحل. ما هي البرمجة الديناميكية؟

البرمجة الديناميكية هي نهج لحل المشكلات حيث يوجد تقسيم إلى مهام فرعية "أبسط" مقارنة بالمهمة الأصلية. كلمة "ديناميكي" قريبة من معنى "حثي": من المفترض أن الإجابة معروفة لبعض المعنى

k

$k$ ، وأريد العثور على إجابة

k + 1

$k + 1$ . في الرياضيات ، يسمى هذا الانتقال الاستقرائي ، وهو الفكرة الرئيسية للبرمجة الديناميكية.

أمثلة بسيطة

إن المهمة الأبرز والأكثر دلالة هي مهمة الحوسبة

n

$n$ رقم تسلسل فيبوناتشي. من المعروف أن التسلسل له الخصائص التالية:

F_{0} = F_{1} = 1 ، F_{n} = F_{n - 1} + F_{n - 2} .

$F_0 = F_1 = 1 ، \ F_n = F_ {n-1} + F_ {n-2}.$

هذا يعني على الفور صيغة التكرار:

int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); }

إذا كان العودية يبحث عن رقم "من النهاية" ، عندئذٍ تحسب الطريقة التالية بالتتابع جميع الأرقام الموجودة بين

0

$0$ و

n

$n$ :

 int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; }

من الواضح أنه كبير بما فيه الكفاية

n

$n$ تعمل هذه الخوارزمية بشكل أسرع: لا تحسب القيم الوسيطة عدة مرات. فكر في مثال أكثر تعقيدًا قليلاً.

مثال 1. أنت تمشي على سلم رسوم. للمضي قدما

i

$i$ الخطوة التي عليك دفعها

a_{i}

$a_i$ عملات معدنية. يمكنك الانتقال إلى الخطوة التالية أو القفز فوق واحدة. المهمة: لتمرير

n

$n$ الخطوات وإنفاق أقل عدد ممكن من العملات المعدنية.

من الواضح أنه عند تجاوز كل خطوة ، نقوم بتقليل عدد "المدفوعات" إلى أدنى حد ، ولكن يمكننا أن نواجه خطوة باهظة الثمن ، والتي نود تجنبها. قم بإنشاء مجموعة من القيم

d

$d$ فيه يوم

j

$j$ - سيكون المكان هو (الحد الأدنى) عدد العملات التي يجب إنفاقها للوصول إليها

j

$j$ الخطوة ال. من الواضح على الفور أن

d_{1} = a_{1} ، d_{2} = a_{2}

$d_1 = a_1 ، \ d_2 = a_2$ . وبعد ذلك سنتخذ الحد الأدنى من الخطوتين السابقتين ونضيف تكلفة الخطوة نفسها:

d_{i} = m i n l e f t (d_{i - 1} ، d_{i - 2} r i g h t) + a_{i} .

$d_i = \ min \ left (d_ {i-1} ، d_ {i-2} \ right) + a_ {i}.$

نغير شروط المشكلة قليلاً: لنفترض أنه في بعض الخطوات يمكنك الحصول على عملات معدنية (وهذا يعني ذلك

a_{k} < 0

$a_k <0$ ) ما الذي يجب تغييره في الخوارزمية بحيث تعطي النتيجة الصحيحة؟

الحل

من الضروري فقط تغيير "بداية" دينامياتنا. إذا لم يجلب لنا الدرج الأول عملات معدنية ، فمن المستحسن القفز فوقه ، إذا

a_{1} < 0

$a_1 <0$ ، من الأفضل أن تخطو وتجمع عملاتك المعدنية. لذا

d_{2} = m i n l e f t (0 ، d_{1} r i g h t) + a_{2}

$d_2 = \ min \ left (0 ، d_1 \ right) + a_2$ .

لنأخذ مثالاً آخر يستخدم ديناميكيات "ثنائية الأبعاد".

مثال 2. يوجد في المتاهة

n م ر ا ت م

$n \ مرات م$ غرف ، كل منها يحتوي على الذهب (في قفص

(i ، j)

$(i، j)$ الأكاذيب

a_{i j}

$a_ {ij}$ ذهب). تتمثل المهمة في تحديد الحد الأقصى لكمية الذهب التي يمكن جمعها بالطريق الأمثل من نقطة

(0 ، 0)

$(0،0)$ إلى هذه النقطة

(n ، m)

$(n، m)$ إذا كنت تستطيع النزول أو إلى اليمين.

لذا ، نريد أن نعرف أفضل طريق للخلية

(i ، j)

$(i، j)$ . يمكننا الوصول إلى هنا من خليتين -

(i - 1 ، j)

$(i-1، j)$ و

(i ، j - 1)

$(i، j-1)$ . بالنظر إلى أن المسارات المثلى لهاتين الخليتين معروفة (يتم تخزينها في بعض الجدول

d

$d$ ) ، ثم إجابة الخلية

(i ، j)

$(i، j)$ تم الحصول عليها على النحو التالي:

d_{i j} = m a x l e f t (d_{i - 1 j} ، d_{i j - 1} r i g h t) + a_{i j} .

$d_ {ij} = \ max \ left (d_ {i-1j} ، d_ {ij-1} \ right) + a_ {ij}.$

هذه مهمة برمجة ديناميكية كلاسيكية أخرى ، التعديلات شائعة جدًا في مهام البرمجة الرياضية. يتم شرح مهمة مماثلة بمزيد من التفصيل هنا .

مهام أكثر صعوبة

إذا رغبت في ذلك ، يمكن ثمل نهج ديناميكي أينما تريد. النظر في مهمة من أرشيف Timus Online Judge.

الصيغة الرياضية للمشكلة هي كما يلي: مطلوب العثور على الحد الأدنى لعدد المصطلحات اللازمة لتحليل رقم معين في مربعات كاملة.

كما كان من قبل ، افترض أننا نعرف إجابات جميع الأرقام

k - 1

$k-1$ التي يتم تخزينها في بعض الصفيف

d

$d$ ونود أن نجد

d_{k}

$d_ {k}$ .

خذ هذا الرقم

k

$k$ وتحليل الحالات التي قد تكون:

$k$ مربع كامل. في هذه الحالة $d_ {k} = 1$ .
ربما الرقم السابق $k-1$ كان مربع كامل. ثم $d_ {k} = d_ {k-1} + 1$ .

بشكل عام ، لا يبدو خيار إضافة وحدة إلى الوحدة السابقة سيئًا للغاية.

نمضي على النحو التالي: نسعى إلى التحلل

k = q^{2} + s

$k = q ^ 2 + s$ مثل هذا

d_{q^{2}} + d_{s} < d_{k - 1} + 1.

$d_ {q ^ 2} + d_s <d_ {k-1} + 1.$

منذ ذلك الحين

q^{2}

$q ^ 2$ - مربع كامل ثم

d_{q^{2}} = 1

$d_ {q ^ 2} = 1$ و

d_{s} < d_{k - 1} ،

$d_s <d_ {k-1} ،$

أي أننا وجدنا قسمًا أفضل ببساطة من

d_{k - 1} + 1

$d_ {k-1} + 1$ ، والجواب في هذه الحالة سيكون

d_{k} = d_{s} + d_{q^{2}} = d_{s} + 1.

$d_k = d_ {s} + d_ {q ^ 2} = d_s + 1.$

نموذج كود Java الذي يقوم بتنفيذ هذه الخوارزمية:

 for(int k = 1; k <= n; k++) { int best = d[k - 1] + 1; //      int q = 1; while(k - q*q >= 0) { // k = q*q + s if(k - q*q == 0) { // k -   best = 1; break; } else if(d[k - q*q] < best) best = d[k - q*q] + 1; q++; } d[k] = best; }

خذ بعين الاعتبار المشكلة التالية. الهدف هو بناء درج من

N

$N$ مكعبات حسب القواعد:

الدرج له خطوتين على الأقل ؛
لا يمكن أن يكون للسلالم خطوتين متطابقتين ؛
خطوات السلالم تصاعديًا (أي أن الدرج التالي أكبر من السابق).

هذه المرة سوف نبني ديناميكيات ثنائية الأبعاد. قم بإنشاء جدول

d

$d$ فيها الموقف

(i ، j)

$(i، j)$ عدد السلالم المكونة من

i

$i$ مكعبات لا يتجاوز ارتفاعها

j

$j$ . إذا نجحت ، فسيكون الجواب لمشكلتنا هو المجموع

s u m l i m i t s_{j = 1}^{n} d_{n j} .

$\ sum \ limits_ {j = 1} ^ n d_ {nj}.$

لذا سنحل مشكلة إيجاد عدد السلالم المكونة لها

i

$i$ مكعبات طويلة

j

$j$ . تظهر الصورة السلالم التي تقع في

d_{74}

$d_ {74}$ :

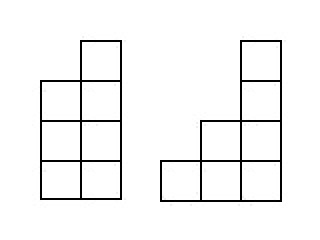
نظرًا لأننا نعرف جميع السلالم ، التي تتكون من عدد أقل من المكعبات ، فسنقوم "بتقسيم" الدرج

(i ، j)

$(i، j)$ العمود الأيمن. والنتيجة سلم ج

i - j

$i-j$ مكعبات. مثال ل

i = 9 ، j = 4

$i = 9، \ j = 4$ :

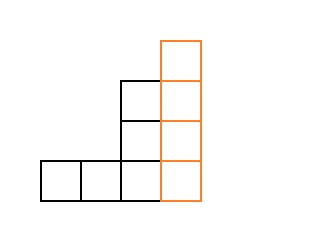
ولكن بالنسبة لهذه السلالم ، فإن النتيجة معروفة بالفعل ، لذلك سنقوم بفرز جميع هذه السلالم مع دورة فيها

k

$k$ واجمع كل النتائج. بهذه الطريقة

d_{i j} = s u m l i m i t s_{k = 1}^{j - 1} d_{i - j k} .

$d_ {ij} = \ sum \ limits_ {k = 1} ^ {j-1} d_ {i-jk}.$

الآن سنقوم بفرز ارتفاعات السلالم:

d_{i j} = s u m l i m i t s_{k = 1}^{j - 1} d_{i - j k} ، j = o v e r l i n e 1 ، i .

$d_ {ij} = \ sum \ limits_ {k = 1} ^ {j-1} d_ {i-jk}، \ j = \ overline {1، i}.$

أخيرا ، يتغير

i

$i$ من

1

$1$ من قبل

n

$n$ نحصل على الجواب.

هام : في عملية بناء المصفوفة الخاصة بنا ، من الضروري النظر

d_{i i} = 1

$d_ {ii} = 1$ ، لأنه بخلاف ذلك سيتم "فقدان" بعض أنواع الدرج (عند "الانقسام") ، ولكن من نافلة القول أن مثل هذا الدرج لا يفي بشروط المشكلة ، لذلك سيكون الجواب هو الرقم

d_{n n} - 1

$d_ {nn} - 1$ .

نموذج كود Java الذي يقوم بتنفيذ هذه الخوارزمية:

 dp = new long[n + 1][n+1]; d[1][1] = 1; d[2][1] = 0; d[2][2] = 1; for(int i = 3; i < n + 1; i++) { for(int j = 2; j <i; j++) { long cnt = 0; for(int k = 1; k < j; k++) { cnt += d[i - j][k]; } d[i][j] = cnt; } d[i][i] = 1; //    } long answer = 0L; for(int i = 0; i <= n; i++) { answer += d[n][i]; } answer--; //

يتم حل المهمة التالية باستخدام صفيف أحادي البعد.

لذا ما لدينا. يعرف المدخل الأول كلمتين. كل علم يعلم كل الكلمات التي يعرفها بنفسه بشرتين وشيوخ. في المقابل ، تم تعليم الصغار عدد الكلمات التي يعرفها بالفعل ، وتم تعليم القديم كلمة واحدة فقط. أنت بحاجة إلى معرفة عدد النمل الذين يعرفون بالضبط

K

$K$ الكلمات (من الضروري استنتاج عدد هذه الوصفات

P

$P$ )

الحل بسيط للغاية. قم بإنشاء مصفوفة

d

$d$ فيه يوم

i

$i$ -المكان الذي سنقوم بتخزين عدد الايجابيات (مودولو

P

$P$ ) الذين يعرفون

i

$i$ الكلمات. يبدأ كل شيء مع ent الأول ، الذي يعرف كلمتين ، لذلك

d_{2} = 1

$d_2 = 1$ . ثم كل شيء بسيط:

جميع الأهل الذين يعرفون عددًا فرديًا من الكلمات قديمة ويمكنهم التعلم فقط من الكلمات السابقة. لذلك للغريب $i: \ d_i = d_ {i-1} ؛$
بالنسبة للأهل الذين يعرفون عددًا زوجيًا من الكلمات ، فإنهم جميعًا الذين تلقوا نفس عدد الكلمات من الجان (صغار) $+$ أولئك الذين تعلموا من السابق (القديم) ؛ أي حتى $i$ لدينا $d_i = d _ {{i \ backslash 2}} + d_ {i-1}$ .

يبقى للتعامل مع نموذج الحساب. حتى لا نخزن أعدادًا ضخمة ، سنتذكر فورًا جميع القيم المعيارية.

نموذج كود Java الذي يقوم بتنفيذ هذه الخوارزمية:

 int[] d = new int[K + 1]; if(K >= 2) d[2] = 1; if(P != 1) { for(int i = 3; i <= K; i++) { if(i % 2 != 0) { d[i] = d[i - 1]; } else { d[i] = ((d[i/2] % P) + d[i - 1] % P) % P; } } } else d[K] = 0;

الموارد المستخدمة:

قاضي Timus Online ؛
قليلا عن البرمجة الديناميكية.
modulo خصائص المقارنة.

البرمجة الديناميكية في مشاكل الأولمبياد

أمثلة بسيطة

مهام أكثر صعوبة

More articles: