مقدمة
أكثر معادلة من النوع البيضاوي هي معادلة بواسون.
يتم تقليل العديد من مشاكل الفيزياء الرياضية إلى حل هذه المعادلة ، على سبيل المثال ، مشاكل توزيع درجة الحرارة الثابتة في مشاكل الانتشار الصلبة ، ومشاكل توزيع المجال الكهروستاتيكي في وسط غير موصل في وجود الشحنات الكهربائية ، وغيرها الكثير.
لحل المعادلات الإهليلجية في حالة العديد من القياسات ، يتم استخدام الطرق العددية لتحويل المعادلات التفاضلية أو أنظمتها إلى أنظمة المعادلات الجبرية. يتم تحديد دقة الحل بخطوة شبكة الإحداثيات وعدد التكرارات وشبكة البت للكمبيوتر [1]
الغرض من المنشور هو الحصول على حل لمعادلة بواسون لظروف حدود ديريتشليت ونيومان ، للتحقق من تقارب طريقة الاسترخاء للحل باستخدام الأمثلة.
تشير معادلة بواسون إلى معادلات من النوع البيضاوي وفي الحالة أحادية البعد لها الشكل [1]:
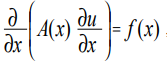
(1)
حيث x هي الإحداثيات ؛ u (x) هي الوظيفة المطلوبة ؛ أ (س) ، و (س) هي بعض وظائف الإحداثيات المستمرة.
نحل معادلة بواسون أحادية البعد للحالة A = 1 ، والتي تأخذ في هذه الحالة الشكل التالي:

(2)
في الفاصل الزمني [xmin، xmax] نحدد شبكة إحداثيات موحدة بخطوة Δ:
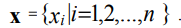
(3)
يمكن تمثيل شروط الحدود من النوع الأول (شروط Dirichlet) للمشكلة قيد النظر على النحو التالي:

(4)
حيث x1، xn هي إحداثيات نقاط حدود المنطقة [xmin، xmax]؛ G1 ، G2 - بعض
الثوابت.
يمكن تمثيل شروط الحدود من النوع الثاني (شروط نيومان) للمشكلة قيد النظر على النحو التالي:

(5)
بتمييز شروط حدود Dirichlet على شبكة إحداثيات موحدة (3) باستخدام طريقة الفروق المحدودة ، نحصل على:
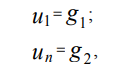
(6)
حيث u1، un هي قيم الدالة u (x) عند النقاط x1، xn ، على التوالي.
بتمييز شروط حدود نيومان على الشبكة (3) ، نحصل على:

(7)
التمييز بين المعادلة (2) لنقاط الشبكة الداخلية ، نحصل على:
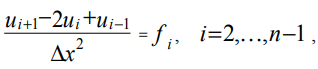
(8)
حيث ui ، fi هي قيم الدالات u (x) و f (x) عند نقطة الشبكة مع الإحداثيات xi.
وبالتالي ، نتيجة لتقدير ، نحصل على نظام معادلات جبرية خطية للأبعاد n تحتوي على معادلات n - 2 من الشكل (8) للنقاط الداخلية للمنطقة والمعادلات (6) و (7) لنقطتين حدوديتين [1].
فيما يلي سرد بايثون للحل العددي للمعادلة (2) بشروط الحدود (4) - (5) على الشبكة (3).
حل الإدراجfrom numpy import* from numpy.linalg import solve import matplotlib.pyplot as plt x0=0
نحصل على:


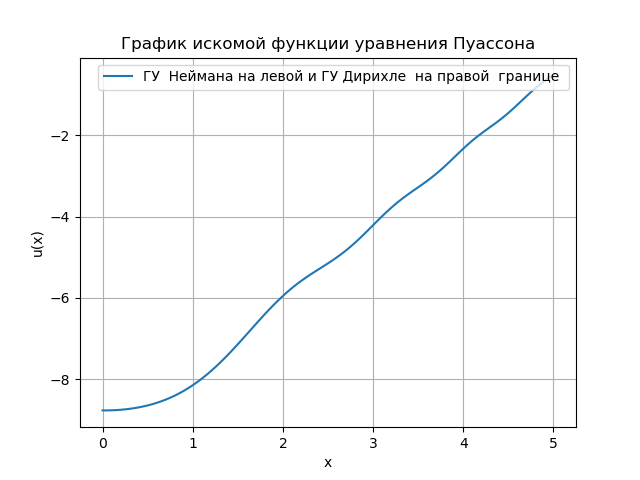

البرنامج الذي طورته في Python مناسب لتحليل شروط الحدود. تستخدم خوارزمية الحل أعلاه في Python وظيفة Numpy - u = linalg.solve (a، bT) .T لحل نظام المعادلات الجبرية ، مما يزيد من السرعة باستخدام المصفوفة المربعة {a}. ومع ذلك ، مع زيادة عدد القياسات ، من الضروري التحول إلى استخدام ثلاث مصفوفات قطرية ، والحل المعقد لها حتى بالنسبة لمهمة بسيطة للغاية ، وجدت مثالًا في المنتدى:
مثال على حل مع ثلاثة مصفوفة قطرية from __future__ import print_function from __future__ import division import numpy as np import time ti = time.clock() m = 1000 A = np.zeros((m, m)) B = np.zeros((m, 1)) A[0, 0] = 1 A[0, 1] = 2 B[0, 0] = 1 for i in range(1, m-1): A[i, i-1] = 7 A[i, i] = 8 A[i, i+1] = 9 B[i, 0] = 2 A[m-1, m-2] = 3 A[m-1, m-1] = 4 B[m-1, 0] = 3 print('A \n', A) print('B \n', B) x = np.linalg.solve(A, B)
برنامج الحل العددي على الزي الموحد في كل اتجاه من مشكلة شبكة Dirichlet لمعادلة الانتشار الحراري
[2]

(9)
نستخدم التقريبات بالاختلافات المركزية في مصطلح الحمل الحراري وطريقة الاسترخاء التكراري ، لاعتماد معدل التقارب على معامل الاسترخاء للحل العددي للمشكلة مع f (x) = 1 و 6 (x) = 0.10. في مهمة الشبكة:

(10)
نحن نمثل المصفوفة A كمجموع المصفوفات القطرية ، السفلية المثلثة والعليا:

(10)
تتوافق طريقة الاسترخاء مع استخدام الطريقة التكرارية :
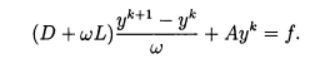
(11)
في

\ الحديث عن الاسترخاء العلوي ، متى
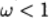
- عن الاسترخاء المنخفض.
قائمة البرامج from numpy import * """ - . .""" def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8): h1 = I1 / n1 h2 = I2 / n2 d = 2. / h1**2 + 2. / h2**2 y = zeros([n1+1, n2+1]) ff = zeros([n1+1, n2+1]) bb = zeros([n1+1, n2+1]) for j in arange(1,n2,1): for i in arange(1,n1,1): ff [i,j] = f(i*h1, j*h2) bb[i,j] = b(i*h1, j*h2)
)
نحصل على:
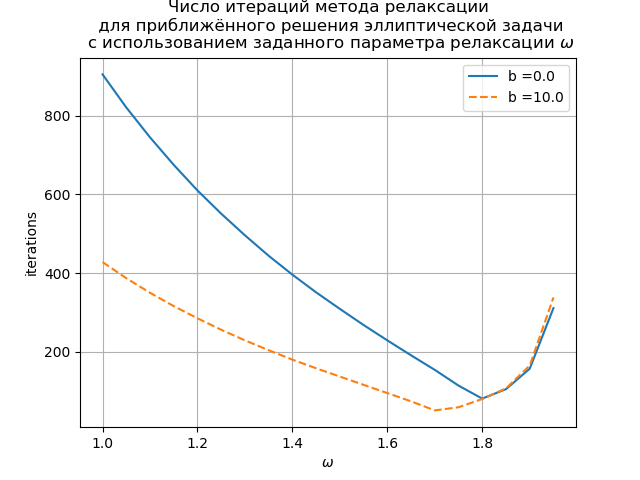
يوضح الرسم البياني اعتماد عدد التكرارات على معلمة الاسترخاء لمعادلة بواسون (ب (س) = 0) ومعادلة انتشار الحمل الحراري (ب (س) = 10). بالنسبة لمعادلة شبكة بواسون ، يتم العثور على القيمة المثلى لمعلمة الاسترخاء تحليليًا ، وتتقارب الطريقة التكرارية عند
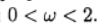
.
الاستنتاجات:
- حل مشكلة الاهليلجيه في بايثون بنظام مرن لتحديد شروط الحدود
- تبين أن طريقة الاسترخاء لديها نطاق مثالي (
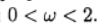 ) معلمة الاسترخاء.
) معلمة الاسترخاء.
المراجع:
- Ryndin E.A. طرق حل مشاكل الفيزياء الرياضية. - تاغونروغ:
دار النشر TRTU ، 2003. - 120 ص. - Vabishchevich P.N. الطرق العددية: ورشة عمل حسابية. - م: بيت الكتاب
ليبروكوم ، 2010. - 320 ص.