المهام من كتاب المدرسة الأول

الجزء الأول
الجزء الثاني
الجزء الثالث

خذ بعين الاعتبار الحل الخوارزمي للمشكلة رقم 38 من كتاب "مهام للأطفال من 5 إلى 15 سنة"

احسب المبلغ:

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(مع خطأ لا يزيد عن 1 ٪ من الإجابة)

فيما يلي خوارزمية لحساب مبالغ جزئية من هذه السلسلة في مخطط (Lisp) في drRacket (يسمح لك drRacket بإجراء حسابات في الكسور العادية):

#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) 

تم حساب المثالين الأخيرين drRacket مع وجود خطأ



يمكن تشغيل هذا البرنامج على الإنترنت ideone.com و codepad.org .



إذا أخذنا في الاعتبار المبالغ الجزئية في الكسور العادية ، يمكننا أن نرى أن مجموع السلسلة هو

$$

$$\ frac {n} {n + 1}$$

دعني أذكرك بذلك $$$\ lim \ frac {n} {n + 1} = \ frac {1} {1+ \ frac {1} {n}} = \ frac {1} {1} = 1$ في $$$n \ to \ infty$

ينظر المجلد الثاني من دورة حساب التفاضل والتكامل 363 (4) في الحالة العامة

$$

$$\ sum \ frac {1} {(\ alpha + n) (\ alpha + n +1)} = \ frac {1} {\ alpha + 1}$$

المهمة من دورة "الرياضيات للمطورين":
أوجد عدد الأعضاء في تسلسل $$$\ frac {2n-1} {4n + 5}$ تقع خارج الفاصل الزمني $$$(1- \ frac {1} {1000}؛ 1+ \ frac {1} {1000})$

دعنا ننتقل إلى الموضوع الرئيسي للمقال.

دعونا نفكر في مثال آخر من كتاب مشكلة.
43 . أعداد الأرانب (فيبوناتشي) ، تشكل تسلسلاً $$$(a_ {1} = 1) ، 1 ، 3 ، 5 ، 8 ، 13 ، 21 ، 34 ، ... ،$ فيه $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ للجميع $$$n = 1، 2، ...$ . ابحث عن أكبر القاسم المشترك للأرقام $$$a_ {100}$ و $$$a_ {99}$ .

الجواب: رقمان فيبوناتشي متجاوران هما نظام مشترك ، أي $$$\ gcd (u_ {n + 1} ، u_ {n}) = 1$
(gcd هو أكبر القاسم المشترك ، أي GCD).

"دليل من كتاب" ما وراء صفحات كتاب الرياضيات "[10-11]


في المهمة التالية ، تحتاج إلى حساب النسبة الذهبية ، $$$\ frac {\ sqrt {5} + 1} {2} \ حوالي 1،618$ . [هذه هي نسبة العرض إلى الارتفاع للبطاقة البريدية التي تظل متشابهة عند قطع مربع يكون جانبه هو الجانب الأصغر من البطاقة البريدية.]

53 . لتسلسل أرقام فيبوناتشي $$$a_ {n}$ المهام 43 تجد حد العلاقة $$$\ frac {a_ {n + 1}} {a_ {n}}$ أثناء السعي $$$n$ إلى ما لا نهاية:

$$

$$\ frac {a_ {n + 1}} {a_ {n}} = 2 ، \ frac {3} {2} ، \ frac {5} {3} ، \ frac {8} {5} ، \ frac { 13} {8} ، \ frac {21} {13} ، \ frac {34} {21}.$$

ضع في اعتبارك الأجزاء التي تمثل الاختلافات بين عضوين متجاورين في السلسلة $$$\ frac {a_ {n + 1}} {a_ {n}}$ .

حتى أعضاء المسلسل $$$\ frac {a_ {n + 1}} {a_ {n}}$ تمثل تسلسل متزايد $$$x_ {n}$

$$

$$\ frac {3} {2} ، \ frac {8} {5} ، \ frac {21} {13} ، ... ،$$

أعضاء الصف الفردية $$$\ frac {a_ {n + 1}} {a_ {n}}$ يمثل تسلسل تنازلي $$$y_ {n}$

$$

$$2 ، \ frac {5} {3} ، \ frac {13} {8} ، ... ،$$

بواسطة ليما الفاصل المضمن (مسار حساب التفاضل والتكامل ، 38)

$$

$$c = \ lim x_ {n} = \ lim y_ {n}$$

لصفنا في نقطة $$$c$ مساواة عادلة $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = \ frac {a_ {n + 1}} {a_ {n}}$

الانقسام $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ على $$$a_ {n + 1}$ نحصل على المعادلة $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = 1 + \ frac {a_ {n}} {a_ {n + 1}}$ .
عن طريق الاستبدال $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = x ، \ frac {a_ {n}} {a_ {n + 1}} = \ frac {1} {x}$ نحصل على المعادلة التربيعية $$$x = 1 + \ frac {1} {x}$ .

إذا قمنا في برنامج Geogebra بتوصيل النقاط 2 و $$$\ frac {3} {2}$ ، $$$\ frac {3} {2}$ و $$$\ frac {5} {3}$ ، $$$\ frac {5} {3}$ و $$$\ frac {8} {5}$ الخ. - احصل على شخصية متشابهة




بشكل عام ، هناك خوارزمية قياسية لحساب أرقام فيبوناتشي في بايثون.
هذه الخوارزمية متاحة على Python.org

 def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100) 

يمكنك التحقق من الرابط
قم بتغيير هذه الخوارزمية بحيث تطبع تقريبًا إلى النسبة الذهبية. بالنسبة للرقمين المتجاورين a و b ، سنقسم المجموع a + b على b

 def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(100) 

يمكنك التحقق من الرابط

فيما يلي بعض المهام من البرنامج التعليمي لـ SICP بشأن النسبة الذهبية.


المثال التالي من كتاب المهام "مهام للأطفال من 5 إلى 15 سنة"
54 . احسب الكسر المستمر اللانهائي

$$

$$1 + \ frac {1} {2 + \ frac {1} {1+ \ frac {1} {2+ \ frac {1} {1+ \ frac {1} {2 + ...}}}}}$$

UPD فكر في المعادلة

$$

$$\ alpha = 1+ \ frac {1} {2 + \ frac {1} {\ alpha}}$$

وفقًا للنظريات 236 و 235 من كتاب "نظرية الأعداد":

$$

$$\ alpha = \ frac {P_ {1} \ alpha + P_ {0}} {Q_ {1} \ alpha + Q_ {0}}$$

نقوم بتكوين جدول القيم $$$P_ {n}$ و $$$Q_ {n}$ في $$$n = 0،1:$



لذلك $$$\ alpha = \ frac {3 \ alpha + 1} {2 \ alpha + 1} ، 2 \ alpha ^ {2} - 2 \ alpha -1 = 0$

ومنذ ذلك الحين $$$\ alpha> 0 ،$ ثم

$$

$$\ alpha = \ frac {1 + \ sqrt {3}} {2}$$

تأمل المشكلة من كتاب "خلف صفحات كتاب الرياضيات" [10-11]
4 . اعرض هذا الرقم $$$\ sqrt {1+ \ sqrt {1 + \ sqrt {1 + ...}}}$ يساوي الرقم $$$\ varphi$ تحديد النسبة الذهبية.

فكر في الخيار $$$x_ {n} = \ sqrt {c + \ sqrt {c + ... + \ sqrt {c}}}$
مسار حساب التفاضل والتكامل ، 35 (2)

بهذه الطريقة $$$x_ {n + 1}$ تم الحصول عليها من $$$x_ {n}$ وفقًا للصيغة

$$

$$x_ {n + 1} = \ sqrt {c + x_ {n}}$$

... حسب النظرية الرئيسية ، الخيارات $$$x_ {n}$ لديها حد محدود $$$a$ . لتحديد ذلك ، نمر إلى الحد الأقصى في المساواة

$$

$$x_ {n + 1} ^ {2} = c + x_ {n} ؛$$

نحصل على مثل هذه الطريقة $$$a$ يفي بالمعادلة التربيعية

$$

$$a ^ {2} = c + a$$

هذه المعادلة لها جذور علامات مختلفة. لكن الحد الذي يهمنا $$$a$ لا يمكن أن تكون سالبة ، وبالتالي فهي تساوي الجذر الموجب:

$$

$$a = \ frac {\ sqrt {4c + 1} + 1} {2}$$

يمكن من خلاله استنتاج أن "النسبة الذهبية" هي حل المعادلة $$$a ^ {2} = c + a$
في $$$c = 1$ .


علاوة على ذلك ، في مسار حساب التفاضل والتكامل ، 35 (3) ، يتم اعتبار خوارزمية لحساب الرقم المعكوس

دع $$$c$ هو أي رقم موجب ، ويوضع $$$x_ {n} = cy_ {n}$ . سيتم استبدال علاقة العودية المكتوبة أعلاه بما يلي:

$$

$$y_ {n + 1} = y_ {n} (2 - cy_ {n})$$

أخذ القيمة الأولية $$$y_ {0}$ تحت الشرط: $$$0 <y_ {0} <\ frac {1} {c}$ نحصل على ذلك $$$y_ {n}$ زيادة رتيبة ، سوف تميل إلى $$$\ frac {1} {c}$ . وفقًا لهذا المخطط ، يتم حساب الرقم المعكوس في آلات العد $$$c$ .

خوارزمية حساب الرقم المعكوس $$$c$ في بيثون:
( Ideone.com و codepad.org )

 def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr 

تأخذ الدالة التبادلية رقمًا كمدخل $$$c$ القيمة الأولية $$$y_ {0}$ عدد التكرارات $$$n$ ويعيد مصفوفة "تقريب" إلى الرقم $$$\ frac {1} {c}$ .
$$$y_ {0} = 0.1$ في $$$c <10$
$$$y_ {0} = 0.01 دولا$ في $$$10 <c <100$
$$$y_ {0} = 0.001$ في $$$100 <c <1000$
الخ.
أمثلة لكيفية عمل الوظيفة المتبادلة مع مختلف $$$c$

 >>> reciprocal(3,0.1,10) 

[0.1 ، 0.17 ، 0.2533 ، 0.31411733000000003 ، 0.3322255689810133 ، 0.3333296519077525 ،
0.3333333332926746، 0.3333333333333333337، 0.3333333333333333337، 0.33333333333333337]

 >>> reciprocal(8,0.1,10) 

[0.1 ، 0.12 ، 0.1248 ، 0.12499968 ، 0.1249999999991808 ، 0.125 ، 0.125 ، 0.125 ، 0.125 ، 0.125]

 >>> reciprocal(5,0.1,10) 

[0.1 ، 0.15000000000000002 ، 0.18750000000000003 ، 0.19921875000000003 ، 0.19999694824218753 ، 0.1999999999534349 ، 0.20000000000000004 ، 0.19999999999999998 ،
0.19999999999999998، 0.19999999999999998]

التفسير الهندسي

دعونا نحاول استخدام طريقة المماس لتقريب الرقم المعكوس.
المماس $$$y = f '(x_ {0}) (x-x_ {0}) + f (x_ {0})$ لتعمل الرسم البياني $$$y = \ frac {1} {x}$ يتم التعبير عنها بواسطة الصيغة $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}}$

استبدال الأرقام $$ بدلا من $$$x_ {0}$ نحصل على معادلات المماس

$$

$$y = 2-x$$

$$

$$y = 1- \ frac {x} {4}$$

$$

$$y = \ frac {2} {3} - \ frac {x} {9}$$

$$

$$y = \ frac {1} {2} - \ frac {x} {16}$$

قم ببناء هذه الرسوم البيانية


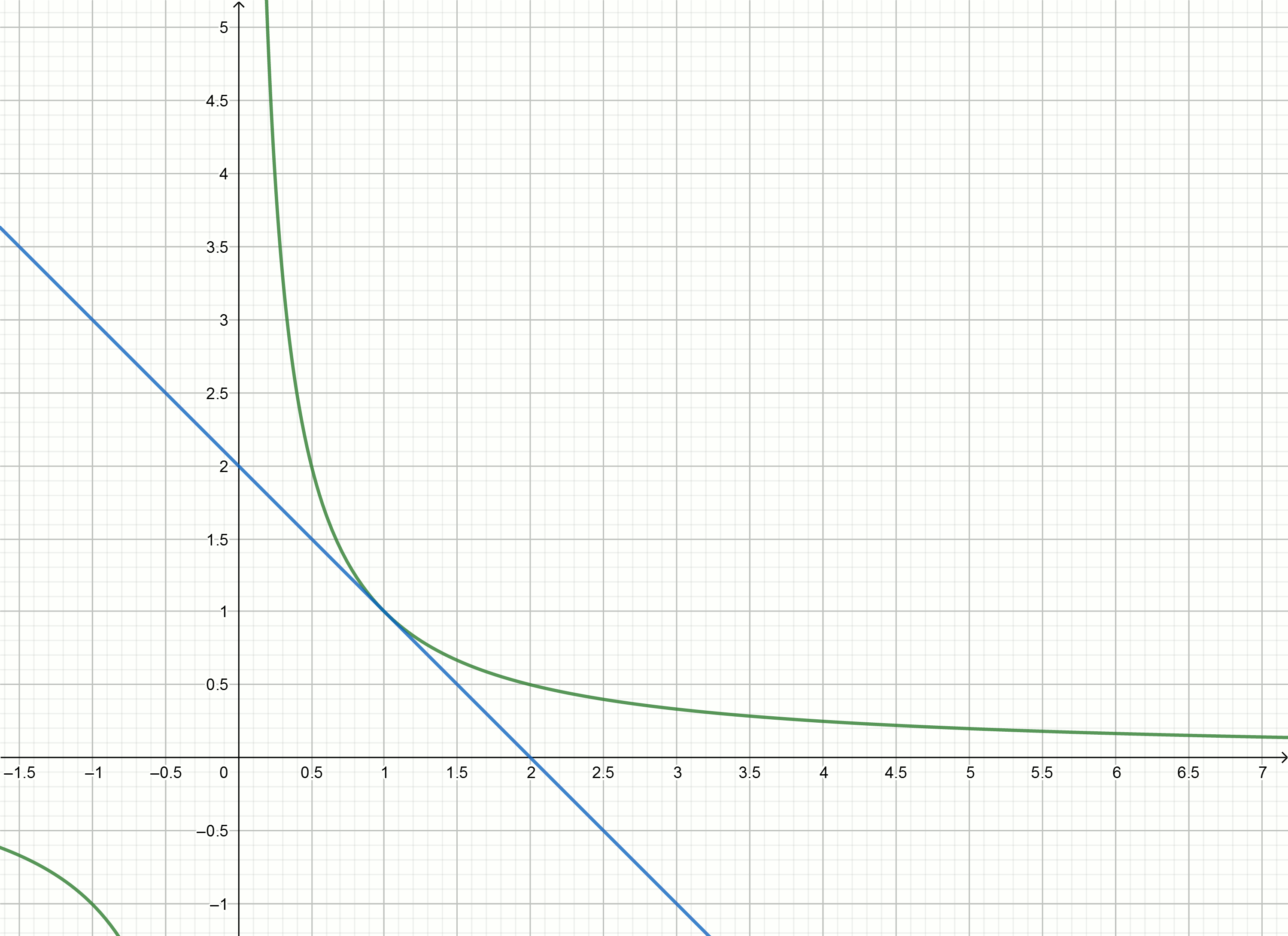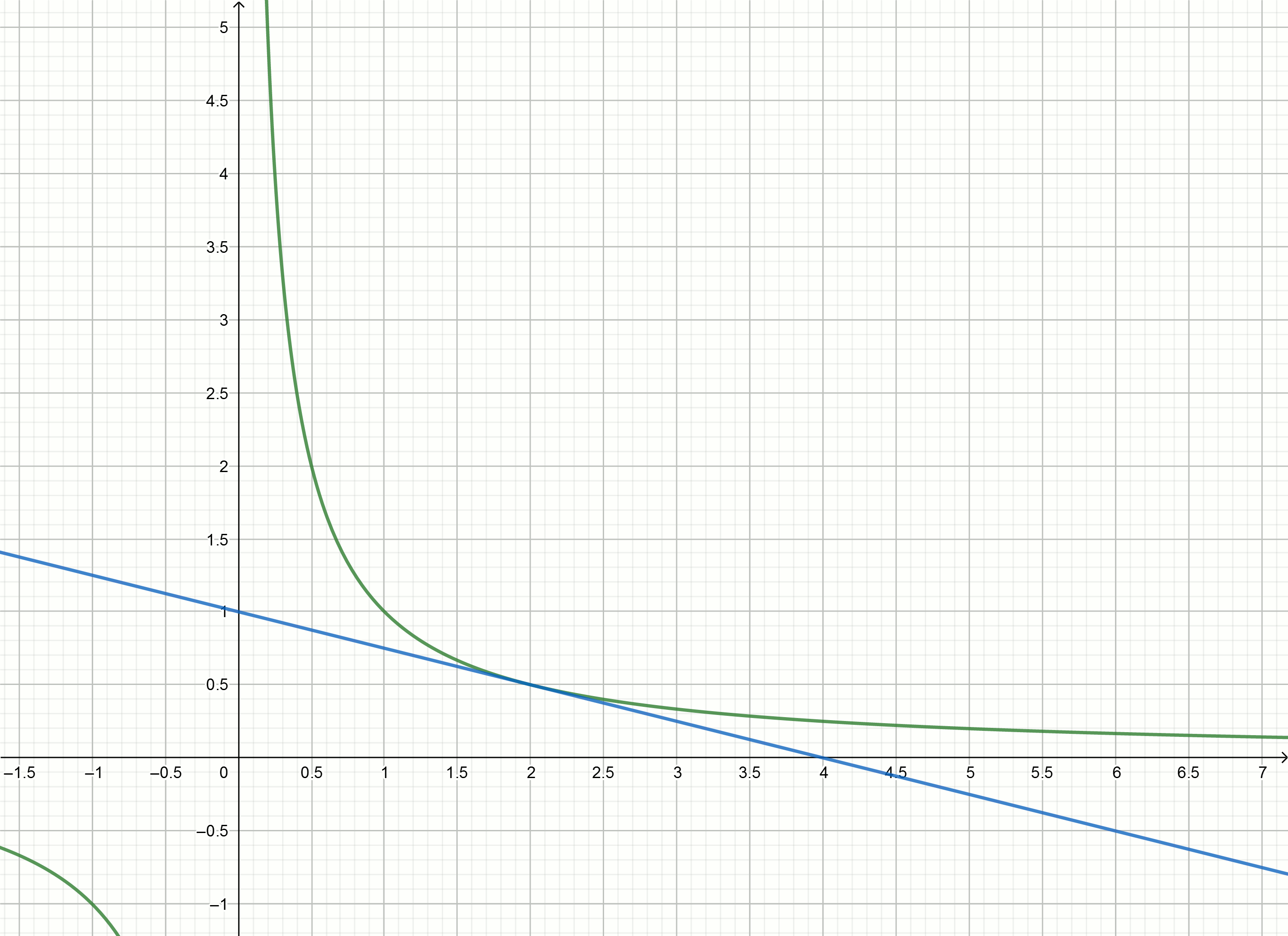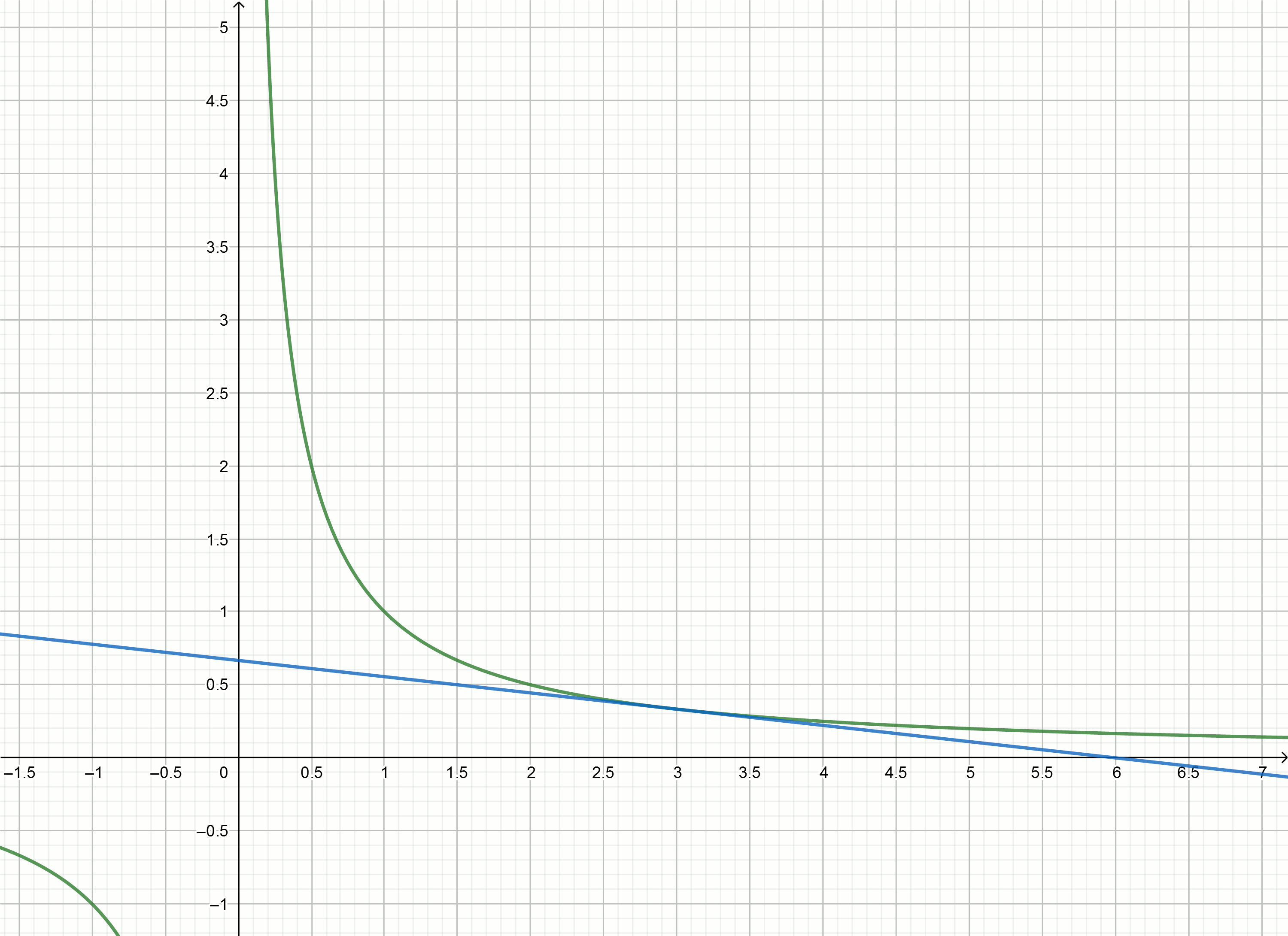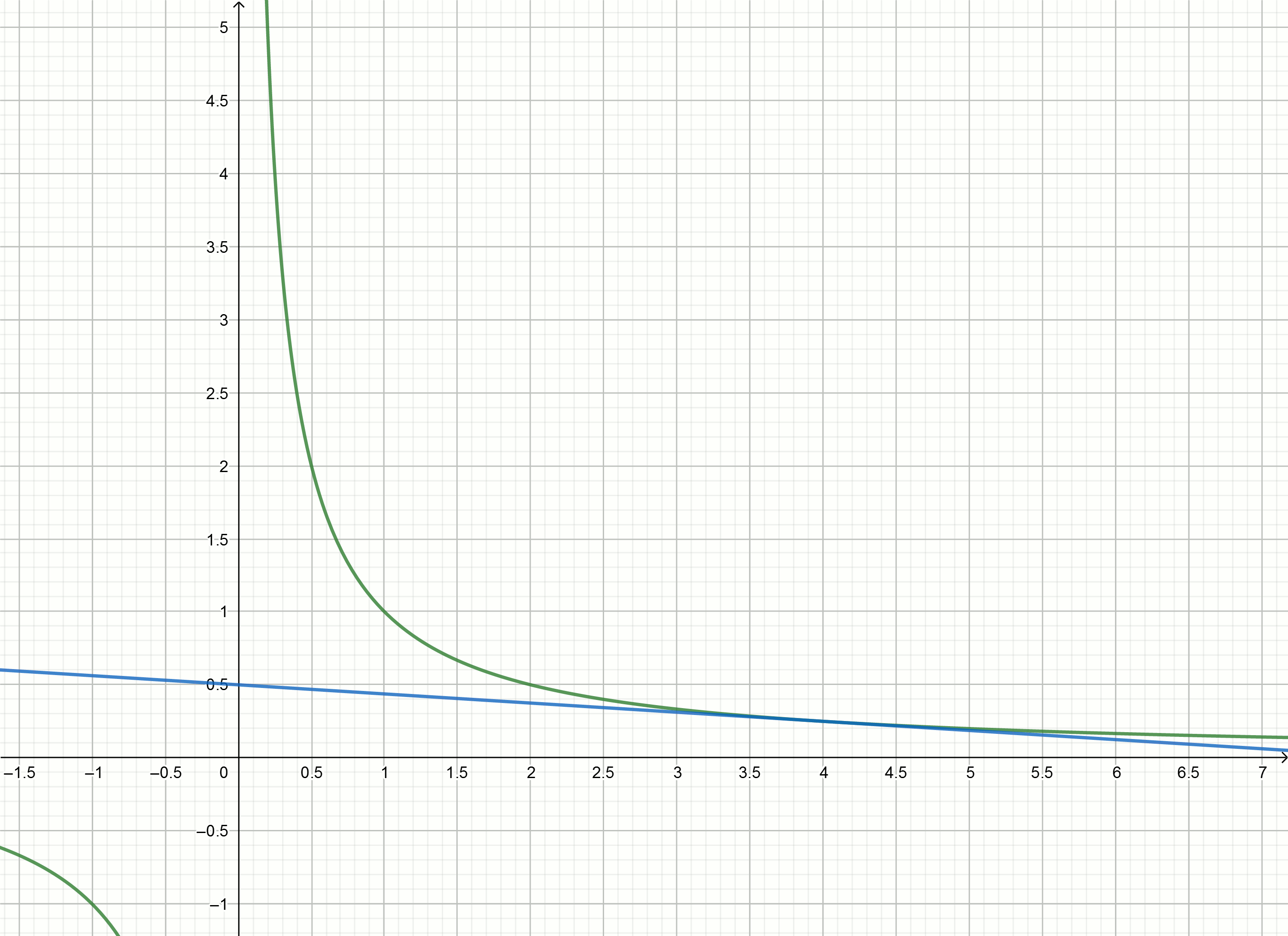
إذا قمت بنقلها إلى أسفل $$$\ alpha$ ، ثم يعبر محور الخراج عند النقطة $$$\ frac {1} {\ alpha}$ .
يتم تحويل معادلة الظل إلى $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - \ alpha$
علاوة على ذلك ، معادلة معادلة المماس بالصفر والتعبير $$$x$ نحصل على المعادلة $$$x = x_ {0} - \ frac {f (x_ {0})} {f '(x_ {0})}$

بدلاً من ذلك $$$f (x_ {0})$ بديل $$$\ frac {1} {x_ {0}} - \ alpha$
بدلاً من ذلك $$$f '(x_ {0})$ بديل $$$- \ frac {1} {x_ {0} ^ {2}}$

نحصل على التعبير $$$x = x_ {0} + (\ frac {1} {x_ {0}} - \ alpha) x_ {0} ^ {2}$
توسيع الأقواس ، نحصل $$$x = x_ {0} + x_ {0} - \ alpha x_ {0} ^ {2}$

استبدل $$ في المعادلة $$$x = x_ {0} (2- \ alpha x_ {0})$ وانظر ما هي القيم التي "ستمر بها" $$$x$ في $$$\ alpha = 2$ نحصل $$

استبدال هذه القيم في المعادلة $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - 2$ نحصل مباشرة

$$

$$y = 0.111 - \ frac {x} {0.897}$$

$$

$$y = 0.222 - \ frac {x} {0.81}$$

$$

$$y = 0.816 - \ frac {x} {0.504}$$

$$

$$y = 0.857 - \ frac {x} {0.49}$$

$$

$$y = 1.5 - \ frac {x} {0.326}$$

$$

$$y = 2 - \ frac {x} {0.25}$$

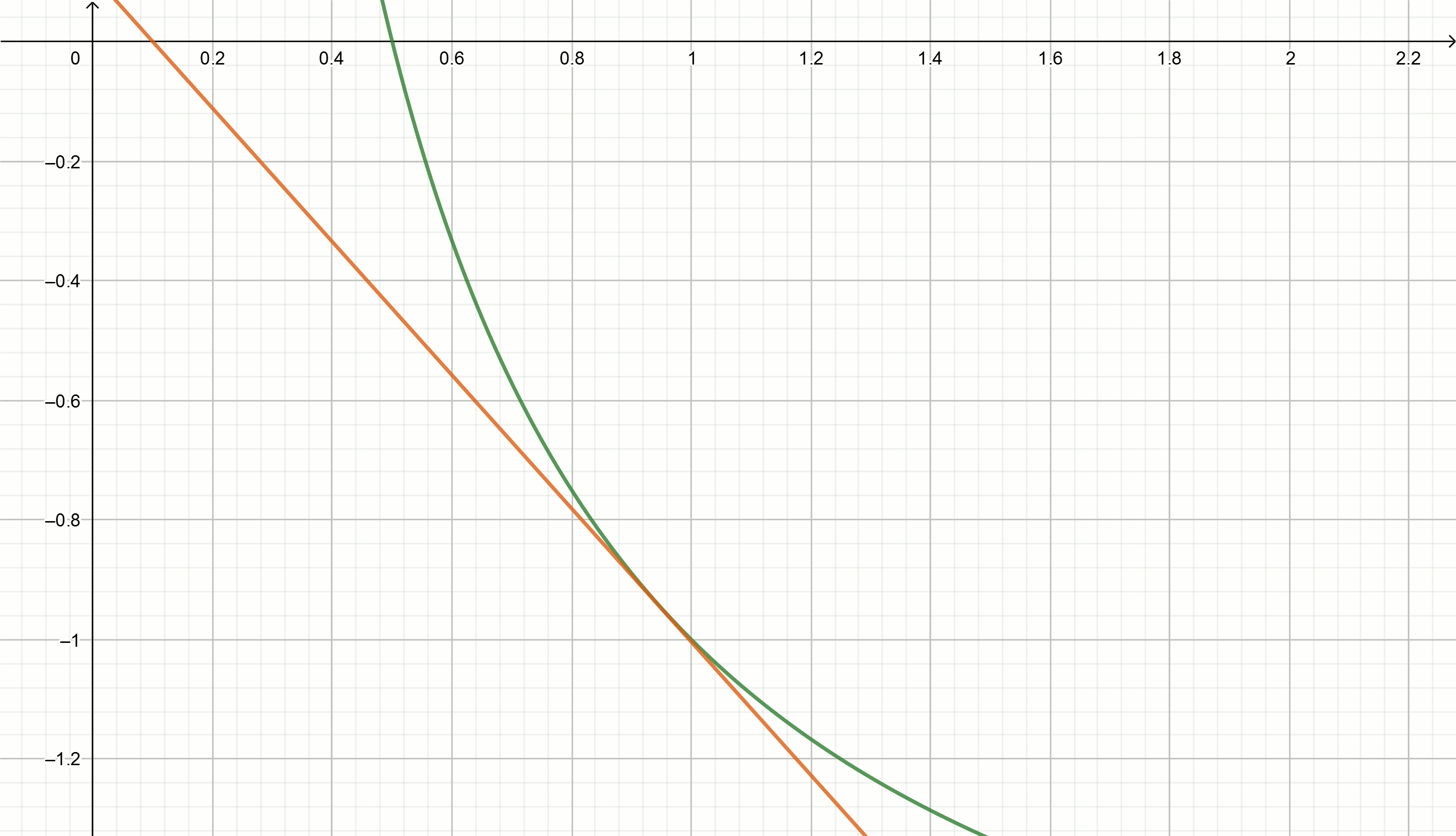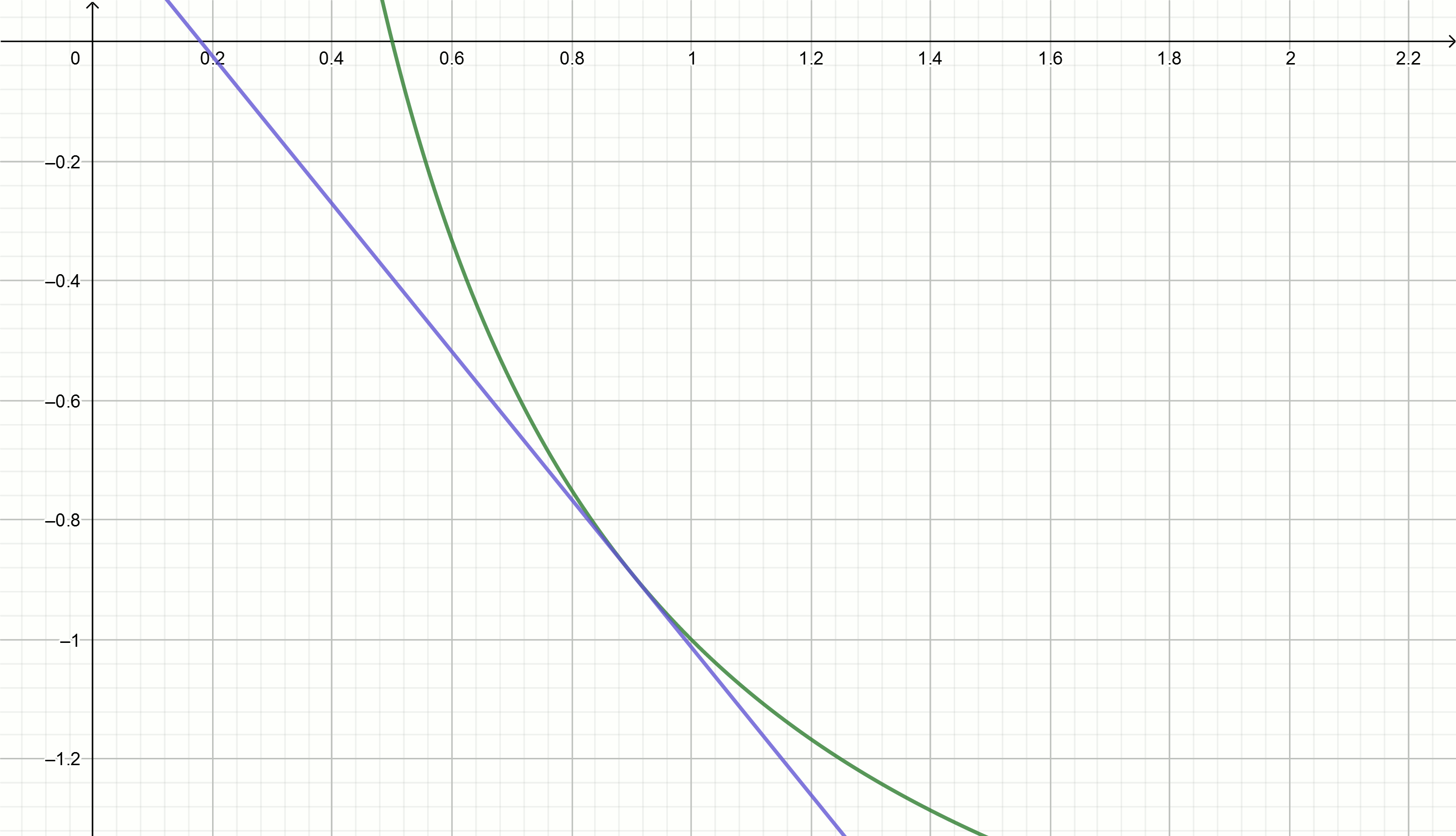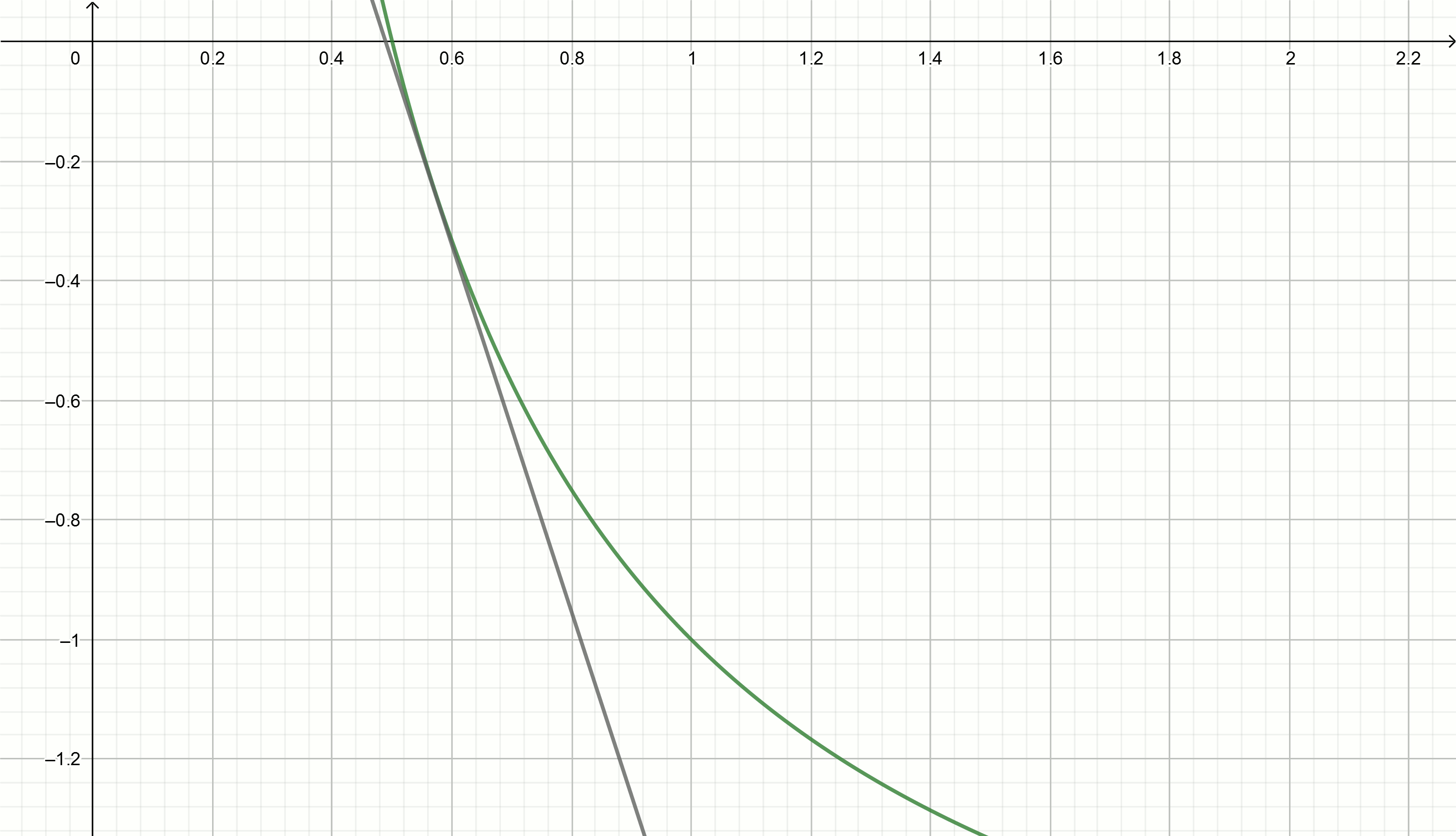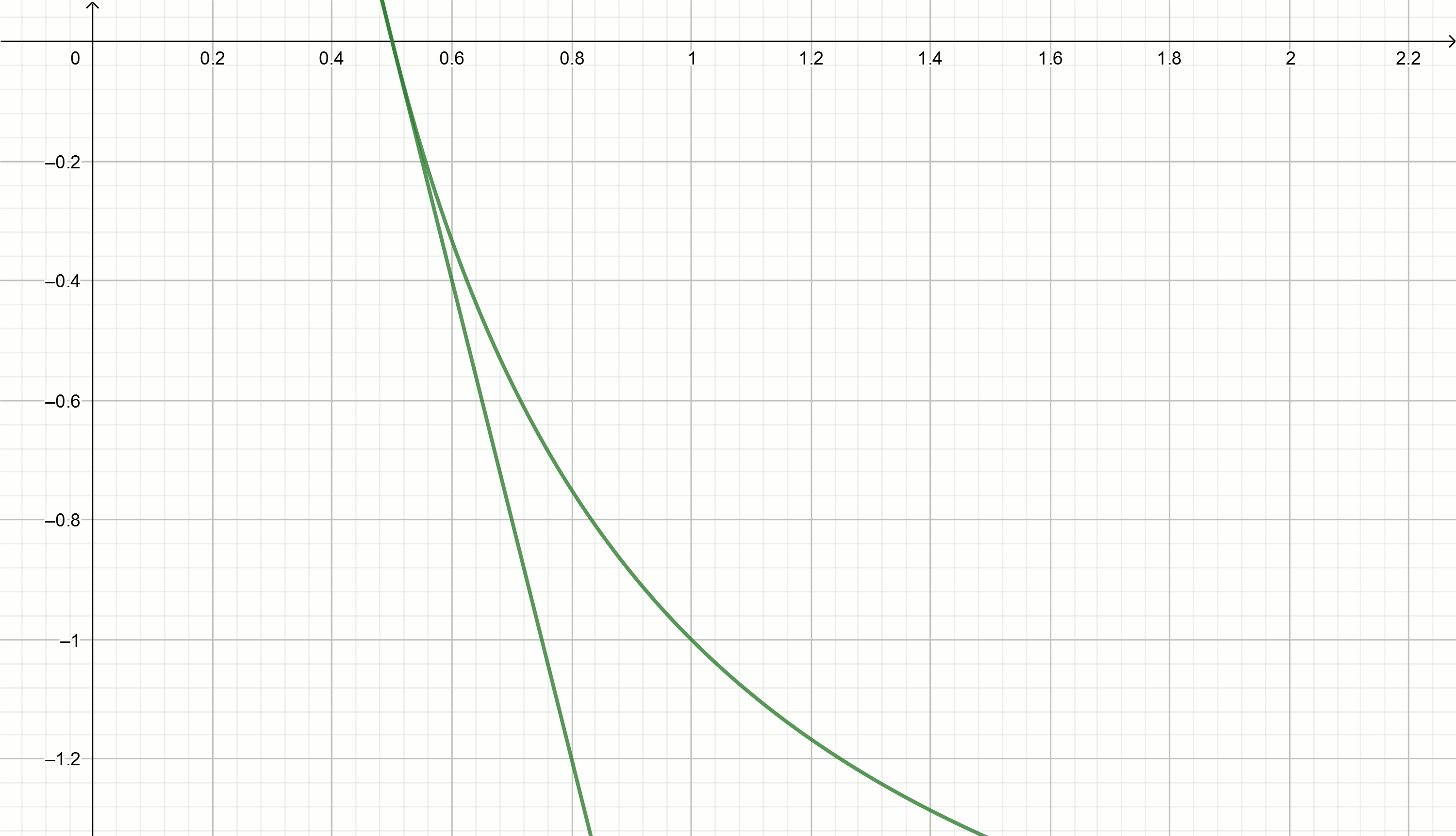
استخراج الجذر التربيعي

بالعودة إلى التعبيرات غير العقلانية ، نعتبر طريقة تكرارية لاستخراج الجذر التربيعي.
سنكتب خوارزمية باستخدام طريقة هيرون التكرارية

$$

$$x_ {n + 1} = \ frac {1} {2} (x_ {n} + \ frac {a} {x_ {n}})$$

 def square_root(a,n): # a -  , n -   x0=1 #    1 arr=[] for i in range(n): arr.append(x0) #      x0=0.5*(x0+a/x0) #      return arr print square_root(2,10) 

codepad.org

حساب الجذر التربيعي باستخدام الكسور المستمرة التي يستخدمها رافائيل بومبيلي

للعثور على القيمة $$$\ sqrt {n}$ ، أولاً نحدد تقريبه بالكامل: $$$\ sqrt {n} = a \ pm r$ أين $$$0 <r <1$ . ثم $$$n = (a \ pm r) ^ {2} = a ^ {2} \ pm 2ar + r ^ {2}$ . من السهل استنتاج ذلك $$$r = {\ frac {| n-a ^ {2} |} {2a \ pm r}}$ . استبدال التعبير الناتج في الصيغة $$$\ sqrt {n} = a \ pm r$ ، نحصل على توسع كسر مستمر:

$$

$$a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}$$

لذا ، يمكننا كتابة خوارزمية استخلاص الجذر التربيعي باستخدام التحلل في جزء مستمر

 def square_root(n,a,n_count): # n- , a -    x0=a #    a arr=[] for i in range(n_count): #       a arr.append(x0-a) #  a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) 

codepad.org

بشكل عام ، يمكن أن تكون الأرقام الحقيقية والمعقدة ، بالإضافة إلى وظائف متغير واحد أو أكثر ، بسط ومقام خاص.
تسمح طريقة استخلاص الجزء الصحيح للمرء بتمثيل عدد غير منطقي في شكل كسر مستمر لا نهائي مع وحدات في البسط (البسط المتكرر يساوي الوحدة).
فيما يلي مثال على التوسع الجزئي المستمر لرقم $$$\ sqrt {5}$ من كتاب الجبر

$$

$$\ sqrt {5} -2 = \ frac {(\ sqrt {5} -2) (\ sqrt {5} +2)} {\ sqrt {5} +2} = \ frac {1} {\ sqrt { 5} +2} دولا$$

بهذه الطريقة $$$\ sqrt {5} = 2+ \ frac {1} {\ sqrt {5} +2}$

حدد الجزء الصحيح من الرقم $$$\ sqrt {5} +2: E (\ sqrt {5} +2) = 4$ . يعني $$$\ sqrt {5} +2$ يمكن تمثيله كـ $$$4 + \ alpha$ . من الواضح أن $$$\ alpha = \ sqrt {5} + 2-4 = \ sqrt {5} -2$ لذلك $$$\ sqrt {5} + 2 = 4 + \ sqrt {5} + 2$ . مرة أخرى ، ندمر اللاعقلانية في بسط المصطلح الثاني:

$$

$$\ sqrt {5} -2 = \ frac {1} {\ sqrt {5} +2}$$

والنتيجة هي:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

لنقم بخطوة أخرى مماثلة:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}}$$

من السهل أن نرى أن عملية عزل الجزء بأكمله وتشكيل جزء مستمر في هذا المثال لا نهاية لها. في كل قاسم جديد سيظهر $$$4$ والمدة $$$\ sqrt {5} -2$ . لذلك ، من الواضح أن $$$\ sqrt {5}$ يمثل ككسر مستمر لانهائي:

$$

$$\ sqrt {5} = [2، 4، 4، 4، ...]$$

الفرضية

إذا $$$d \ in \ mathbb {N} ، \ sqrt {d} \ notin \ mathbb {N}$ ثم الجزء المستمر من الرقم $$$\ sqrt {d} + [\ sqrt {d}]$ دورية بحتة.
أثبت Evarist Galois هذه الفرضية.

على سبيل المثال إذا إلى الجزء غير الدوري من الكسر $$$[1؛ 2،2،2، ...] = \ sqrt {2}$ أضف الجزء كله $$$[\ sqrt {2}] = 1$ ثم نحصل على جزء دوري بحت $$$[2،2،2، ...]$ .

$$$\ sqrt {3} = [1؛ 1،2، ...] ؛$
$$$\ sqrt {3} +1 = [2،1، ...]$

$$$\ sqrt {5} = [2؛ 4،4،4، ...]؛$
$$$\ sqrt {5} +2 = [4،4،4، ...]$

$$$\ sqrt {6} = [2؛ 2،4، ...] ؛$
$$$\ sqrt {6} +2 = [4،2، ...]$

$$$\ sqrt {13} = [3؛ 1،1،1،1،6، ...] ؛$
$$$\ sqrt {13} +3 = [6،1،1،1،1،1، ...]$


إذا كان في التحلل الجذري وفقا لطريقة بومبيلي

$$

$$\ sqrt {n} = a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ { 2} |} {2a \ pm \ cdots}}}}}}} دولا$$

أضف إلى الفصل الأول $$$a$ ، نحصل على جزء دوري بحت

$$

$$\ sqrt {n} + a = 2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}}$$

يبقى إحضار الكسر إلى شكل مألوف أكثر (مع وحدات في البسط).
اقسم البسط ومقام الكسر على $$$| n-a ^ {2} |$ نحصل على التعبير

$$

$$\ sqrt {n} + a = 2 a \ pm {\ frac {1} {\ frac {2a} {| na ^ {2} |} \ pm {\ frac {1} {2a \ pm {\ frac { 1} {\ frac {2a} {| na ^ {2} |} \ pm \ cdots}}}}}}$$

بهذه الطريقة

$$

$$\ sqrt {2} +1 = 2+ \ frac {1} {\ frac {2} {1} + \ frac {1} {2 + \ frac {1} {\ frac {2} {1} +. ..}}} = [2،2،2، ...]$$

$$

$$\ sqrt {3} +1 = 2+ \ frac {1} {\ frac {2} {2} + \ frac {1} {2 + \ frac {1} {\ frac {2} {2} +. ..}}} = [2،1، ...]$$

$$

$$\ sqrt {5} +2 = 4+ \ frac {1} {\ frac {4} {1} + \ frac {1} {4 + \ frac {1} {\ frac {4} {1} +. ..}}} = [4،4،4، ...]$$

$$

$$\ sqrt {6} +2 = 4+ \ frac {1} {\ frac {4} {2} + \ frac {1} {4 + \ frac {1} {\ frac {4} {2} +. ..}}} = [4،2، ...]$$

$$

$$\ sqrt {13} +3 = 6+ \ frac {1} {\ frac {6} {4} + \ frac {1} {6 + \ frac {1} {\ frac {6} {4} +. ..}}} = [6، \ frac {3} {2}، ...]$$

سنكتب برنامجًا يحسب تقريب الكسر المستمر $$$[6، \ frac {3} {2}، ...]$

 #lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) 

codepad.org
في الخطوة الرابعة نحصل $$$6 \ frac {3818} {6305}$ وهو يساوي $$$6.60555114 ...$ بينما $$$\ sqrt {13} +3 \ تقريبًا 6.60555127$ .




PS حل المشكلة ("مشاكل للأطفال من 5 إلى 15 سنة")
27 . يثبت أن ما تبقى من قسمة عدد $$$2 ^ {p-1}$ رئيس غريبة
$$$p$ يساوي $$$1$
(أمثلة: $$$2 ^ {2} = 3a + 1، 2 ^ {4} = 5b + 1، 2 ^ {6} = 7c + 1، 2 ^ {10} -1 = 1023 = 10 \ cdot 93)$ .
يتم تناول هذه المشكلة في مقالة Amazing Adventures of Continued Fractions of the Quantum magazine.

كتب:
"مهام للأطفال من 5 إلى 15 سنة" V. I. Arnold.
"مسار حساب التفاضل والتكامل" G.M Fichtenholtz
"نظرية العدد" A. A. Buchstab
"خلف صفحات كتاب الرياضيات" N.N. Vilenkin، L. P. Shibasov، Z. F. Shibasova
"Algebra" N. Ya. Vilenkin، R. S. Guter، S. I. Schwarzburd
الحساب الرقمي Ercegovac Milos D. ، Lang Tomas
"هيكل وتفسير برامج الكمبيوتر" هارولد أبيلسون ، جيرالد سسمان

انظر أيضًا
المقال "في مهمة واحدة لم تعد تُعرض في المقابلة".
مدونة Spice IT Recruitment تنشر مهام المقابلة في العديد من الشركات.
مهام المقابلات في Yandex.
في هذا الفيديو ، يحل A. Savvateev المشاكل في المقابلات في Tesla.