مقدمة
تؤدي العديد من المشكلات التطبيقية إلى الحاجة إلى إيجاد حل عام لنظام المعادلات غير الخطية. لم يتم العثور على حل تحليلي عام لنظام المعادلات غير الخطية. هناك طرق عددية فقط.
وتجدر الإشارة إلى حقيقة مثيرة للاهتمام أن أي نظام من المعادلات على الأعداد الحقيقية يمكن تمثيله بمعادلة واحدة مكافئة ، إذا أخذنا جميع المعادلات في الشكل
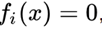
قم بتثبيتها وطيها.
بالنسبة للحل العددي ، يتم استخدام الطرق التكرارية للتقريبات المتتالية (التكرار البسيط) وطريقة نيوتن في التعديلات المختلفة. يتم تعميم العمليات التكرارية بشكل طبيعي على حالة نظام المعادلات غير الخطية من النموذج:
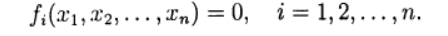
(1)
دلالة بواسطة
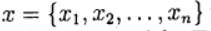
متجه المجهول وتحديد دالة المتجه
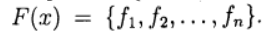
ثم يكتب النظام (1) في شكل معادلة:
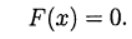
(2)
الآن ، دعنا نعود إلى Python المحبوبة ونلاحظ تفوقها بين لغات البرمجة التي تريد أن تتعلم [1].
هذه الحقيقة هي حافز إضافي للنظر في الأساليب العددية في بيثون. ومع ذلك ، هناك رأي بين عشاق Python بأن وظائف المكتبة الخاصة ، مثل
scipy.optimize.root ، spsolve_trianular ، newton_krylov ، هي أفضل خيار لحل المشكلات بالطرق العددية.
من الصعب الاختلاف مع هذا ، إذا كان ذلك فقط لأن تنوع الوحدات قد أدى أيضًا إلى رفع Python إلى قمة الشعبية. ومع ذلك ، هناك حالات عندما ، حتى مع الفحص السريع ، استخدام الطرق المعروفة مباشرة دون استخدام وظائف خاصة لمكتبة SciPy يعطي أيضًا نتائج جيدة. وبعبارة أخرى ، الجديد هو القديم المنسي بشكل جيد.
لذلك ، في المنشور [2] ، استنادًا إلى التجارب الحاسوبية التي تم إجراؤها ، ثبت أن وظيفة المكتبة newton_krylov ، المصممة لحل أنظمة كبيرة من المعادلات غير الخطية ، لديها نصف السرعة من خوارزمية TSLS + WD
(المربعات الصغرى بخطوتين) التي تنفذها مكتبة NumPy.
الغرض من هذا المنشور هو مقارنة عدد التكرارات والسرعة ، والأهم من ذلك ، نتيجة حل مشكلة نموذج في شكل نظام من مائة معادلة جبرية غير خطية باستخدام وظيفة مكتبة scipy.optize.root وطريقة نيوتن التي تم تنفيذها باستخدام مكتبة NumPy.
إمكانيات حل Scipy.optimize.root لحل أنظمة المعادلات الجبرية غير الخطية عدديًا
تم اختيار وظيفة المكتبة scipy.optimize.root كقاعدة للمقارنة لأنها تحتوي على مكتبة واسعة من الطرق المناسبة للتحليل المقارن.
scipy.optimize.root (
fun، x0، args = ()، method = 'hybr'، jac = None، tol = None، callback = None، ptions = None )
المرح - وظيفة متجه لإيجاد الجذر.
x0 –الظروف الأولية لإيجاد الجذور
الطريقة:hybr - يتم استخدام تعديل باول للطريقة الهجينة ؛
lm - يحل أنظمة المعادلات غير الخطية باستخدام طريقة المربعات الصغرى.
على النحو التالي من التوثيق [3] ، فإن الطرق
broyden1 و broyden2 و anderson و linearmixing و diagbroyden و sexymixing و krylov هي طرق نيوتن الدقيقة. المعلمات المتبقية "اختيارية" ويمكن العثور عليها في الوثائق.
طرق حل أنظمة المعادلات غير الخطية
يمكن قراءة المواد الواردة أدناه بالفعل في الأدبيات ، على سبيل المثال ، في [4] ، لكنني أحترم قارئي ، ومن أجل راحته ، أقدم اشتقاق الطريقة في شكل مختصر ، إن أمكن. أولئك الذين
لا يحبون الصيغ تخطي هذا القسم.
في طريقة نيوتن ، يتم تحديد تقريب جديد لحل نظام المعادلات (2) من حل
نظام المعادلات الخطية :
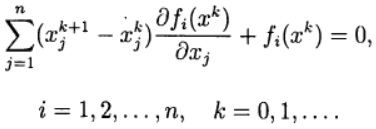
(3)
حدد مصفوفة جاكوبي:
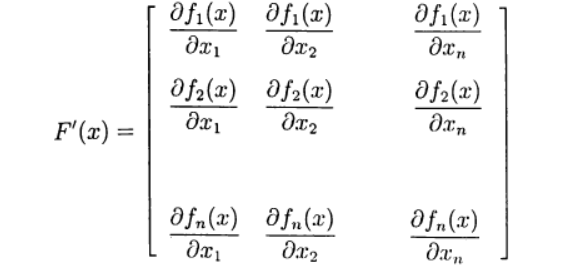
(4)
نكتب (3) بالصيغة التالية:

(5)
يمكن كتابة العديد من الطرق ذات الخطوة الواحدة للحل التقريبي لـ (2) عن طريق القياس مع الطرق التكرارية المكونة من طبقتين لحل أنظمة المعادلات الجبرية الخطية في الشكل:
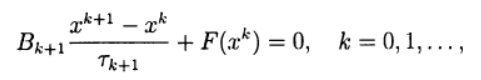
(6)
أين
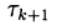
هي معلمات تكرارية ، أ
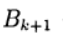
- مصفوفة مربعة n x n لها معكوس.
عند استخدام السجل (6) ، تتوافق طريقة نيوتن (5) مع الاختيار:
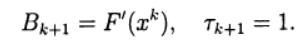
نظام المعادلات الخطية (5) لإيجاد تقريب جديد

يمكن حلها بشكل متكرر. في هذه الحالة ، لدينا عملية تكرارية من مرحلتين مع تكرارات خارجية وداخلية. على سبيل المثال ، يمكن إجراء عملية تكرارية خارجية وفقًا لطريقة نيوتن ، ويمكن إجراء التكرارات الداخلية على
أساس طريقة Seidel التكرارية.عند حل أنظمة المعادلات غير الخطية ، يمكن للمرء استخدام نظائرها المباشرة للطرق التكرارية القياسية المستخدمة في حل أنظمة المعادلات الخطية. تعطي طريقة Seidel غير الخطية كما تم تطبيقها على الحل (2):
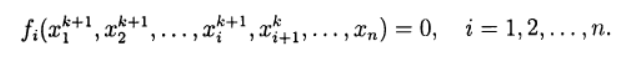
(7)
في هذه الحالة ، يمكن الحصول على كل مكون للتقريب الجديد من حل المعادلة غير الخطية على أساس طريقة التكرار البسيطة وطريقة نيوتن في تعديلات مختلفة. وهكذا ، نأتي مرة أخرى إلى طريقة تكرارية من مرحلتين يتم فيها تنفيذ التكرارات الخارجية وفقًا لطريقة Seidel ، ويتم إجراء التكرارات الداخلية باستخدام طريقة نيوتن.
ترتبط الصعوبات الحسابية الرئيسية في تطبيق طريقة نيوتن للحل التقريبي لأنظمة المعادلات غير الخطية
بالحاجة إلى حل نظام معادلات خطية مع مصفوفة جاكوبي في كل تكرار ، وتتغير هذه المصفوفة من التكرار إلى التكرار. في طريقة نيوتن المعدلة ، يتم عكس مصفوفة جاكوبي مرة واحدة فقط:
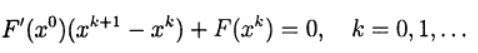
(8)
اختيار وظيفة النموذج
مثل هذا الاختيار ليس مهمة بسيطة ، لأنه مع زيادة عدد المعادلات في النظام وفقًا لزيادة عدد المتغيرات ، يجب ألا تتغير نتيجة الحل ، لأنه بخلاف ذلك من المستحيل تتبع صحة حل نظام المعادلات عند مقارنة طريقتين. أحمل الحل التالي لوظيفة النموذج:
n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f
تنشئ الدالة f نظامًا من المعادلات غير الخطية n ، والتي لا يعتمد حلها على عدد المعادلات وهو يساوي الوحدة لكل من المتغيرات n.برنامج للاختبار على دالة نموذجية مع نتائج حل نظام المعادلات الجبرية غير الخطية باستخدام وظيفة المكتبة optize.root لطرق مختلفة لإيجاد الجذور
from numpy import* from scipy import optimize import time ti = time.clock() n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) sol = optimize.root(f,x0, method='krylov') print('Solution:\n', sol.x) print('Krylov method iteration = ',sol.nit) print('Optimize root time', round(time.clock()-ti,3), 'seconds')
نجحت واحدة فقط من الطرق الواردة في الوثائق [3] في
اختبار نتيجة حل دالة نموذجية ، وهي طريقة "كريلوف" .
حل ن = 100:
الحل:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
تكرار طريقة كريلوف = 4219
تحسين وقت الجذر 7.239 ثانية:
حل ن = 200الحل:
[1.00000018 0.99999972 0.99999985 1.00000001 0.99999992 1.00000049
0.99999998 0.99999992 0.99999991 1.00000001 1.00000013 1.00000002
0.9999997 0.99999987 1.00000005 0.99999978 1.0000002 1.00000012
1.00000023 1.00000017 0.99999979 1.00000012 1.00000026 0.99999987
1.00000014 0.99999979 0.99999988 1.00000046 1.00000064 1.00000007
1.00000049 1.00000005 1.00000032 1.00000031 1.00000028 0.99999992
1.0000003 1.0000001 0.99999971 1.00000023 1.00000039 1.0000003
1.00000013 0.9999999 0.99999993 0.99999996 1.00000008 1.00000016
1.00000034 1.00000004 0.99999993 0.99999987 0.99999969 0.99999985
0.99999981 1.00000051 1.0000004 1.00000035 0.9999998 1.00000065
1.00000061 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.00000059 1.00000056
1.00000047 1.00000016 1.00000018 0.99999988 1.00000061 1.00000002
1.00000033 1.00000034 1.0000004 1.00000046 1.00000009 1.00000024
1.00000017 1.00000014 1.00000054 1.00000006 0.99999964 0.99999968
1.00000005 1.00000049 1.0000005 1.00000028 1.00000029 1.00000027
1.00000027 0.9999998 1.00000005 0.99999974 0.99999978 0.99999988
1.00000015 1.00000007 1.00000005 0.99999973 1.00000006 0.99999995
1.00000021 1.00000031 1.00000058 1.00000023 1.00000023 1.00000044
0.99999985 0.99999948 0.99999977 0.99999991 0.99999974 0.99999978
0.99999983 1.0000002 1.00000016 1.00000008 1.00000013 1.00000007
0.99999989 0.99999959 1.00000029 1.0000003 0.99999972 1.00000003
0.99999967 0.99999977 1.00000017 1.00000005 1.00000029 1.00000034
0.99999997 0.99999989 0.99999945 0.99999985 0.99999994 0.99999972
1.00000029 1.00000016]
تكرار طريقة كريلوف = 9178
تحسين وقت الجذر 23.397 ثانية
الخلاصة: مع زيادة عدد المعادلات بمعامل اثنين ، فإن ظهور الأخطاء في الحل ملحوظ. مع زيادة أخرى في n ، يصبح الحل غير مقبول ، وهو أمر ممكن بسبب التكيف التلقائي مع الخطوة ، وهو نفس السبب وراء انخفاض حاد في الأداء. ولكن هذا مجرد تخميني.
برنامج للاختبار على دالة نموذجية مع نتائج حل نظام المعادلات الجبرية غير الخطية باستخدام برنامج مكتوب في Python 3 مع مراعاة العلاقات (1) - (8) للعثور على الجذور باستخدام طريقة نيوتن المعدلة
برنامج البحث عن الجذور حسب طريقة نيوتن المعدلة from numpy import* import time ti = time.clock() def jacobian(f, x): h = 1.0e-4 n = len(x) Jac = zeros([n,n]) f0 = f(x) for i in arange(0,n,1): tt = x[i] x[i] = tt + h f1= f(x) x[i] = tt Jac [:,i] = (f1 - f0)/h return Jac, f0 def newton(f, x, tol=1.0e-9): iterMax = 50 for i in range(iterMax): Jac, fO = jacobian(f, x) if sqrt(dot(fO, fO) / len(x)) < tol: return x, i dx = linalg.solve(Jac, fO) x = x - dx print ("Too many iterations for the Newton method") n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) x, iter = newton(f, x0) print ('Solution:\n', x) print ('Newton iteration = ', iter) print('Newton method time', round(time.clock()-ti,3), 'seconds')
حل ن = 100:
الحل:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
تكرار نيوتن = 13
زمن طريقة نيوتن 0.496 ثانية
حل n = 200:
الحل:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1.]
تكرار نيوتن = 14
وقت طريقة نيوتن 1.869 ثانية
للتأكد من أن البرنامج يحل النظام حقًا ، نعيد كتابة وظيفة النموذج لتجنب الجذر بقيمة 1 في النموذج:
n=10 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i] f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f
نحصل على:
الحل:
[0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
تكرار نيوتن = 16
زمن طريقة نيوتن 0.046 ثانية
الخلاصة:
يعمل البرنامج أيضًا عندما تتغير وظيفة النموذج.الآن نعود إلى وظيفة النموذج الأولي ونتحقق من نطاق أوسع لـ n ، على سبيل المثال ، عند 2 و 500.
ن = 2
الحل:
[1. 1.]
تكرار نيوتن = 6
زمن طريقة نيوتن 0.048 ثانية
ن = 500
ن = 500الحل:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
تكرار نيوتن = 15
وقت طريقة نيوتن 11.754 ثانية
الاستنتاجات:
برنامج مكتوب في Python باستخدام طريقة نيوتن المعدلة ، عند حل أنظمة المعادلات غير الخطية من دالة النموذج المعينة ، لديه استقرار أكثر للحل مما كان عليه عند الحل باستخدام وظيفة المكتبة optimize.root (f، x0، method = 'krylov') لطريقة Krylov. فيما يتعلق بسرعة الاستنتاج النهائي ، فمن المستحيل الرسم بسبب النهج المختلف للتحكم التدريجي.
المراجع:
- تقييم لغات البرمجة 2018.
- Cooper I.V. ، Faleychik B.V. العمليات التكرارية غير المصفوفة مع كبت جذر متوسط مربع الخطأ للأنظمة الكبيرة من المعادلات غير الخطية.
- scipy.optimize.root.
- Vabishchevich P.N. الطرق العددية: ورشة عمل حسابية. - م: دار الكتاب "ليبروكوم" ، 2010. - 320 ص.