بناء مدارات الأجرام السماوية باستخدام Python

أنظمة مرجعية لتحديد المدار

للعثور على مسارات الحركات النسبية في الميكانيكا الكلاسيكية ، يتم استخدام افتراض الوقت المطلق في جميع الإطارات المرجعية (سواء بالقصور الذاتي أو غير القصوري).

باستخدام هذا الافتراض ، نعتبر حركة نفس النقطة في إطارين مرجعيين مختلفين $$$K$ و $$$K ^ {'}$ التي يتحرك الثاني بالنسبة إلى الأولى بسرعة تعسفية $$$\ vec {V (t)} = \ dot {\ vec {R (t)}}$ أين $$$\ vec {R (t)}$ ناقل نصف القطر يصف موضع أصل نظام الإحداثيات $$$K ^ {'}$ بالنسبة للإطار المرجعي $$$K$ )

سنصف حركة نقطة في النظام $$$K ^ {'}$ ناقلات الشعاع $$$\ vec {r ^ {'}} (ر)$ موجه من أصل النظام $$$K ^ {'}$ إلى الموقع الحالي للنقطة. ثم حركة النقطة قيد النظر بالنسبة للإطار المرجعي $$$K$ وصفها ناقلات الشعاع $$$\ vec {r (t)}$ :

$$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ ، (1)

والسرعة النسبية $$$\ vec {v (t)}$

$$$\ vec {v} (t) = \ dot {\ vec {r ^ {'}}} (t) + \ dot {\ vec {R}} (t)$ ، (2)

أين $$$\ dot {\ vec {r ^ {'}}} (ر)$ - سرعة النقطة بالنسبة للنظام $$$K ^ {'}$ ؛ $$$\ dot {\ vec {R}} (t)$ -سرعة الإطار $$$K ^ {'}$ بالنسبة للإطار المرجعي $$$K$ .



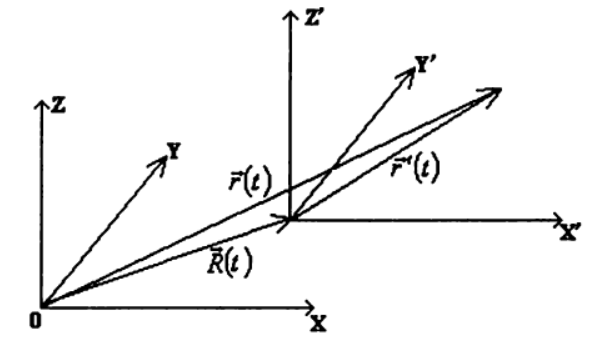
وبالتالي ، لإيجاد قانون حركة نقطة في إطار مرجعي تعسفي $$$K$ ضروري:

1) وضع قانون حركة النقطة - $$$\ vec {r ^ {'}} (ر)$ بالنسبة للإطار المرجعي $$$K ^ {'}$ ؛
2) وضع قانون الحركة - $$$\ vec {R} (t)$ أنظمة مرجعية $$$K ^ {'}$ بالنسبة للإطار المرجعي $$$K$
3) تحديد قانون الحركة للنقطة - $$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ بالنسبة للإطار المرجعي $$$K$ .

بناء مدار القمر في الإطار المرجعي المركزي

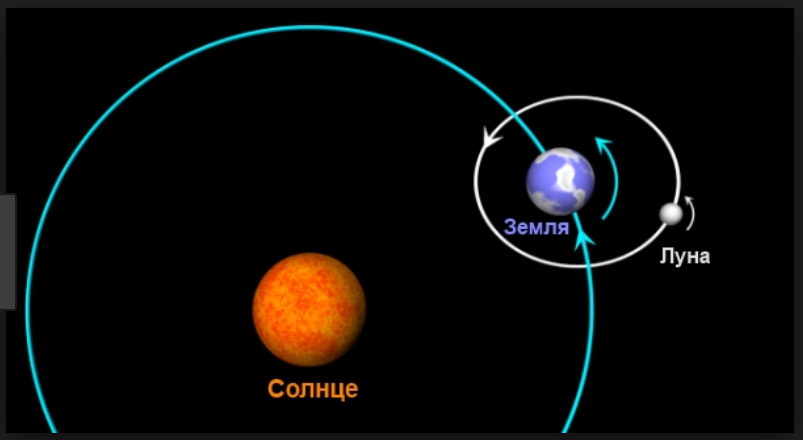
في النظام المرجعي مركزية الشمس (النظام $$$K$ ) تتحرك الأرض في دائرة نصف قطرها
$$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ كم (فترة التداول $$$T_ {1} = 3،156 \ cdot 10 ^ {7}$ ق.). القمر ، بدوره ، يتحرك حول الأرض (النظام K ') حول دائرة نصف قطرها $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ كم (فترة التداول $$$T_ {2} = 2.36 \ cdot 10 ^ {6}$ ق كما هو معروف [1،2] ، عندما تتحرك نقطة مادية على طول دائرة نصف قطرها $$$R$ بسرعة زاوية ثابتة $$$\ omega$ تتغير إحداثيات ناقلات الشعاع المرسومة من الأصل إلى الوضع الحالي للنقطة وفقًا للقانون:

$$

$$\ vec {R (t)} = \ binom {R \ cdot cos (\ omega \ cdot t + \ varphi _ {0})} {R \ cdot sin (\ omega \ cdot t + \ varphi _ {0})} = \ binom {R \ cdot cos (\ frac {2 \ pi} {T}) + \ varphi _ {0})} {R \ cdot sin (\ frac {2 \ pi} {T} + \ varphi _ { 0})} ، (3)$$

أين $$$\ varphi _ {0}$ - المرحلة الأولية التي تميز موضع الجسيم في الوقت المناسب $$$t = 0$ ، التي سنفترض في المستقبل أنها تساوي الصفر. استبدال في (3) $$$R$ على $$$R_ {1}$ و $$$R_ {2}$ والاستبدال في (1) ، نحصل على اعتماد ناقلات نصف قطر القمر في نظام إحداثيات مركزية الشمس في الوقت المحدد:

$$

$$\ vec {r (t)} = \ binom {x (t)} {y (t)} = \ binom {R_ {2} cos (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} cos (\ frac {2 \ pi} {T_ {1}} t)} {R_ {2} sin (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} sin (\ frac {2 \ pi} {T_ {1}} t)} ، (4)$$

يعبر التعبير (4) عن مدار القمر ( $$$y = y (x (t))$ ) في شكل معلمي ، حيث المعلمة هي الوقت. لبناء المدار المطلوب باستخدام Python ، قمنا بتعيين نصف قطر المدارات وفترات دوران الأرض والقمر.

تتحرك الأرض في نظام إحداثيات مركزية الشمس ( $$$K$ ) نصف قطر مدارها وفترة الثورة متساويان على التوالي $$$R_ {1} = 1.496 \ cdot 10 ^ {8} كم ، T_ {1} = 3.156 \ cdot 10 ^ {7} s$ يتحرك القمر حول الأرض في نظام إحداثيات ( $$$K ^ {'}$ ) نصف قطر مدارها وفترة الثورة متساويان على التوالي $$$R_ {2} = 3.844 \ cdot 10 ^ {5} كلم ، T_ {2} = 2.36 \ cdot 10 ^ {6} s$ .

في ضوء (4) نحدد وظائف اعتماد الإحداثيات في الوقت المحدد:

$$

$$\ binom {(X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} \ cdot t) ، Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} \ cdot t)} {x (t) = R_ {2} \ cdot cos (\ frac {2 \ pi} {T_ {2}} \ cdot t) ، y (t) = R_ {2} \ cdot sin (\ frac {2 \ pi} {T_ {2}} \ cdot t)} ، (5)$$

باستخدام (5) نحصل على زوج من الإحداثيات لمدار القمر:

$$

$$\ binom {X_ {g} (t) = X (t) + x (t)} {Y_ {g} (t) = Y (t) + y (t)} ، (6)$$

نحدد عدد النقاط التي يتم فيها حساب الإحداثيات N = 1000 والوقت المنفصل على فترة دوران الأرض $$$dt = \ frac {T_ {1}} {N}$ . سنكتب برنامجًا وننشئ رسمًا بيانيًا لمنطقة تغيير الإحداثيات الإيجابية:


نحصل على:


الشكل 1

يسمح لك الجدول الزمني الذي تم إنشاؤه بتوسيع مهمة التدريب ومعرفة مدار القمر إذا كان نصف قطر مدار القمر $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ . . من الواضح للقارئ الذي ليس لديه حتى معرفة خاصة في علم الفلك أن القمر لا يمكن أن يكون له مثل هذا المدار في المجالات غير الجاذبية للأرض ، ويستخدم نصف قطر افتراضي لدراسة شروط ظهور الحلقات . سنقوم بإجراء التغييرات المناسبة على البرنامج:


نحصل على:


الشكل 2

مقارنة مدارات القمر الموضحة في الشكل. 1 و 2 ، نجد اختلافاتهما الكبيرة. لشرح أسباب هذه الاختلافات ، من الضروري مقارنة السرعات الخطية للقمر في الحالتين الأولى والثانية والسرعة الخطية للأرض.

منذ اتجاه السرعة الخطية للأرض نسبة إلى الشمس ، وكذلك اتجاه السرعة الخطية للقمر نسبة إلى الأرض ، تتغير في الوقت ، وتبقى السرعة ثابتة في الحجم.

كخاصية كمية لنسبة السرعات الخطية للقمر والأرض في نظام إحداثيات مركزية الشمس ، يجب على المرء أن يختار الفرق بين وحدة السرعة الخطية للأرض وإسقاط السرعة الخطية للقمر على اتجاه ناقل السرعة الخطية للأرض:

$$

$$v_ {o} (t) = \ اليسار | \ vec {V} (t) \ right | - \ frac {(\ vec {V} (t) \ cdot \ vec {v} (t))} {\ left | \ vec {V} (t) \ right |} ، (7)$$

نحدد الوظائف التي تصف قوانين التغيير لمكونات سرعة الأرض والقمر:

$$

$$\ start {matrix} V_ {x} (t) = \ frac {d} {dt} X (t) و V_ {y} (t) = \ frac {d} {dt} Y (t) & \\ vx (t) = \ frac {d} {dt} x (t)، vy (t) = \ frac {d} {dt} y (t) \ end {matrix}، (8)$$

لتحديد السرعة الناتجة ، مع مراعاة الإسقاط ، نستخدم العلاقة:

$$$D (t) = \ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} - \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}} \ cdot \ frac {V_ {x} (t) \ cdot vx (t) + V_ {y} (t) \ cdot vy (t)} {\ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} \ cdot \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}}} ، (9)$

سنكتب برنامجًا مع مراعاة (5) و (8) و (9) ونصف قطر مدار القمر $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ كلم.:


نحصل على:


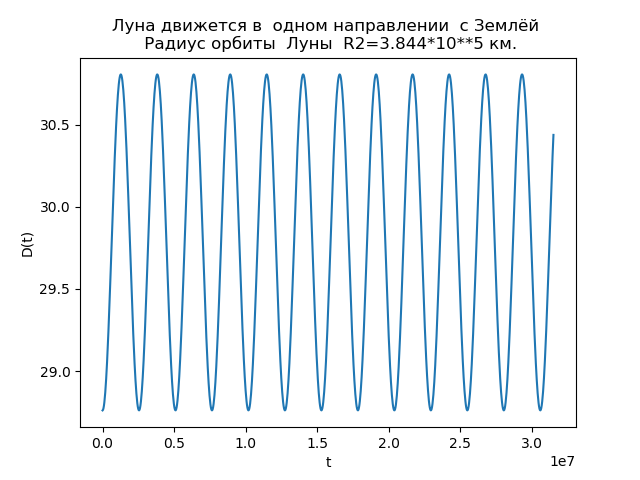الشكل 3.

سنكتب برنامجًا مع مراعاة (5) و (8) و (9) ونصف قطر مدار القمر R2 = 3.844 * 10 ** 7 كم:


نحصل على:


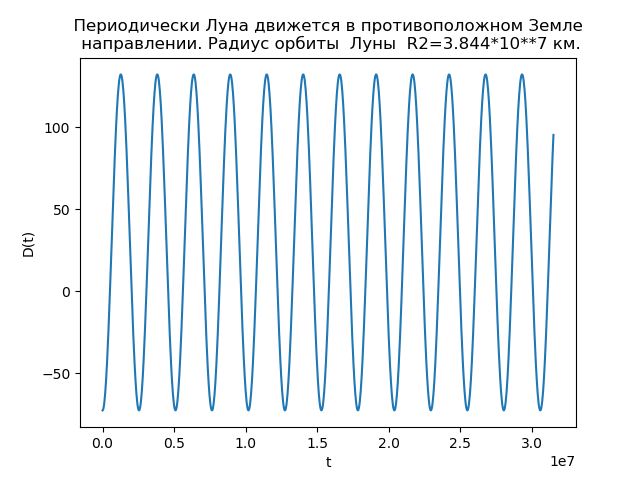الشكل 4.

يسمح لنا تحليل التبعيات بشرح سبب الاختلافات في المدارات. الدالة D (t) لـ $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ km دائمًا إيجابية ، أي أن القمر يتحرك دائمًا في اتجاه حركة الأرض ولا يتشكل حلقات. في $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ قيمة الكيلومتر $$$D (t)$ يأخذ قيمًا سلبية ، وهناك أوقات يتحرك فيها القمر في الاتجاه المعاكس لاتجاه حركة الأرض ، وبالتالي فإن المدار له حلقات. كان هذا هو معنى استخدام مدار القمر غير الموجود في الحسابات.

بناء مدار المريخ في الإطار المرجعي المرتبط بالأرض

.


في النظام المرجعي الشمسي (النظام K) ، تتحرك الأرض في دائرة نصف قطرها $$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ كيلومتر، فترة التداول $$$T_ {1} = 365.24 دولارً$ اليوم ، يتحرك المريخ على طول القطع الناقص ، المحور شبه الرئيسي له $$$am = 2.28 \ cdot 10 ^ {8}$ كم ، فترة ثورة المريخ $$ أيام. ، غريب الأطوار للمدار $$$e = $ 0.09$ [3]. يتم وصف حركة الأرض بواسطة متجه نصف القطر R (t) المحدد بواسطة التعبير (3). يرجع ذلك إلى حقيقة أن مدار المريخ هو القطع الناقص ، التبعيات $$$x = x (t)، y = y (t)$ من الوقت يتم تعيينها بشكل بارز [4]:

$$$x (\ varepsilon) = a_ {m} \ cdot (cos (\ varepsilon) -e)$ ، (10)

$$$y (\ varepsilon) = a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot sin (\ varepsilon)$ ، (11)

$$$t (\ varepsilon) = \ frac {T_ {m}} {2 \ pi} \ cdot (\ varepsilon-e \ cdot sin (\ varepsilon))$ ، (12)

تقارن ثورة ناقصة كاملة مع تغيير في المعلمة <img $$$\ varepsilon$ من 0 إلى $$$2 \ pi$ . لبناء مدار المريخ ، من الضروري حساب إحداثيات ناقلات نصف القطر في نفس الوقت الذي يصف موقع الأرض والمريخ في الإطار المرجعي المركزي ، ثم وفقًا للعلاقة $$$\ vec {r ^ {'}} (t) = \ vec {r} (t) - \ vec {R} (t)$ حساب إحداثيات المريخ في الإطار المرجعي المرتبط بالأرض.

لبناء مدار المريخ في الإطار المرجعي المرتبط بالأرض ، نستخدم المعلمات المعطاة سابقًا لمداري الأرض والمريخ ، والعلاقات (10) - (12) ، وكذلك علاقات إحداثيات الأرض:

$$$X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} t)$ ، (13)

$$$Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} t)$ ، (14)

وتجدر الإشارة إلى أن عدد فترات ثورة المريخ حول الشمس هي $$$K = 9$ ثم عدد النقاط التي يجب أن يتم الحساب عندها وسيتم تحديد المسافة بينهما من العلاقات:

$$$N = 4000 \ cdot K، \ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i، i = 0 ... N$ (15)


نحصل على:


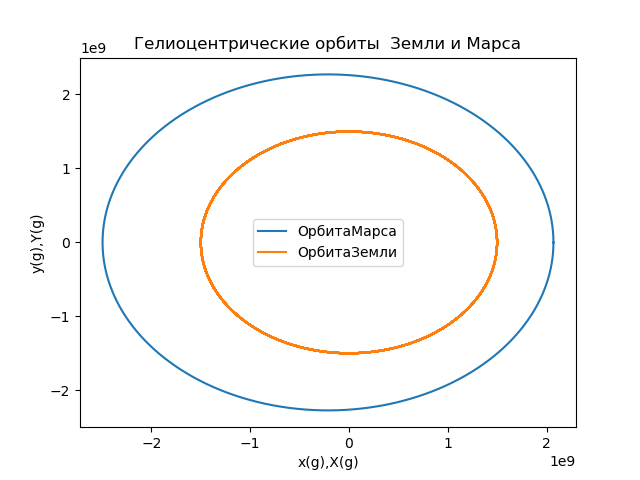الشكل 5

نحسب إحداثيات متجه نصف القطر الذي يصف موقع المريخ في الإطار المرجعي المتصل بالأرض ، وننشئ المدارات (الشكل 6) باستخدام العلاقة:

$$$x1_ {i} = x (\ varepsilon_ {i}) - X (t (\ varepsilon_ {i})) ، y1_ {i} = y (\ varepsilon_ {i}) - Y (t (\ varepsilon_ {i}) ))$ (16)


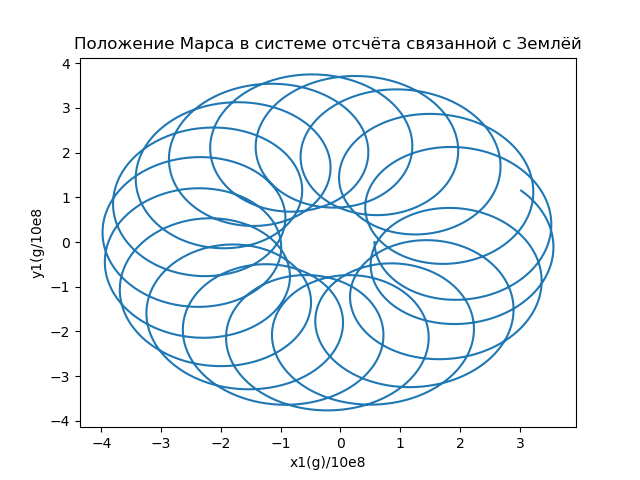الشكل 6

خاصية أخرى مهمة لحركة المريخ (في المقام الأول لرحلات الفضاء بين الكواكب) هي المسافة بين الأرض والمريخ s (t) ، والتي يتم تحديدها بواسطة معامل متجه نصف القطر الذي يصف موقع المريخ في الإطار المرجعي المرتبط بالأرض. ويبين الشكل 7 اعتماد المسافة بين الأرض والمريخ على الوقت المقيس بالسنوات الأرضية.


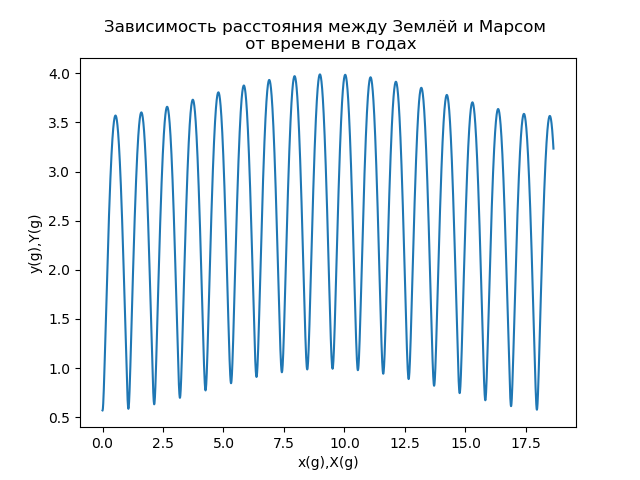الشكل 7

يوضح تحليل الاعتماد المبين في الشكل 7 أن المسافة بين الأرض والمريخ هي وظيفة دورية معقدة للوقت. إذا استخدمنا مصطلحات نظرية الإشارة [5] ، فيمكننا القول عن الاعتماد s (t) أنها إشارة معدلة السعة ، والتي عادة ما يتم تمثيلها على أنها نتاج وظيفتين لوظيفة عالية التردد (الناقل) ووظيفة التردد المنخفض التي تحدد تعديل السعة (المغلف) :

$$$u (t) = (\ bar {u} + a \ cdot sin (\ omega_ {1} t)) \ cdot (1+ \ Delta a \ cdot sin (\ omega_ {2} t))$ (17)

أين $$$\ bar {u}$ - المكون الثابت للدالة $$$u (t)$ ؛ $$$a$ - اتساع الإشارة ؛ $$$\ omega_ {1}$ - تردد الموجة الحاملة ؛ $$$\ Delta a$ - اتساع الوظيفة التي تحدد عمق تشكيل الاتساع ؛ $$$\ omega_ {2}$ - تردد وظيفة التشكيل.

من الشكل 7 يمكن ملاحظة أن فترة الموجة الحاملة تقارب 2 سنة ، وفترة وظيفة التشكيل حوالي 17 سنة] 6].

بناء مدار مركزية مذنب هالي

آخر مرة مر بها مذنب هالي عبر الحضيض (أقرب نقطة مدار إلى الشمس) في 9 فبراير 1986. (تعتبر الشمس نفسها موجودة في الأصل).

كانت الإحداثيات ومكونات السرعة لمذنب هالي متساوية $$$p_ {0} = (0.325514 ، 0.459460 ، 0.166229)$ و $$$v_ {0} = (–9.096111، –6.916686، –1.305721)$ على التوالي ، ويتم التعبير عن المسافة هنا بوحدات طول فلكية - a.u.d. أو ببساطة au. (الوحدة الفلكية ، أي طول شبه الشبه الرئيسي الرئيسي لمدار الأرض) ، والوقت بالسنوات. في وحدات القياس هذه ، يكون لمعادلات الحركة ثلاثية الأبعاد للمذنب الشكل:

$$

$$\ left \ {\ start {matrix} \ frac {d ^ {2} x} {dt ^ {2}} = - \ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { د ^ {2} y} {dt ^ {2}} = - \ frac {\ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } = - \ frac {\ mu \ cdot z} {r ^ {3}} \ end {matrix} \ right.، (18)$$

(18)

حيث: $$$\ mu = 4 \ pi ^ {2} ، r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


نحصل على:









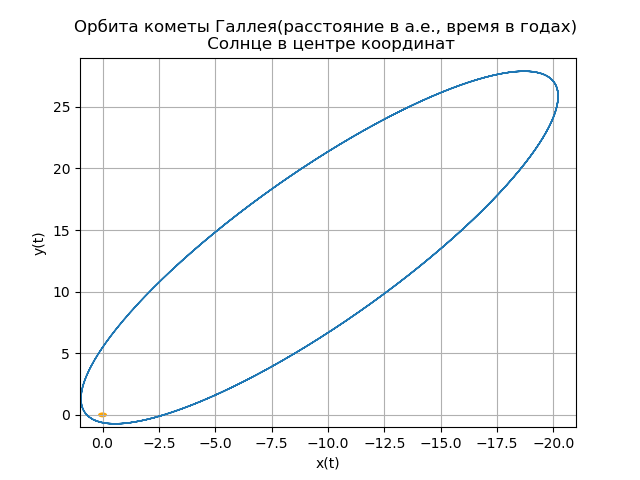
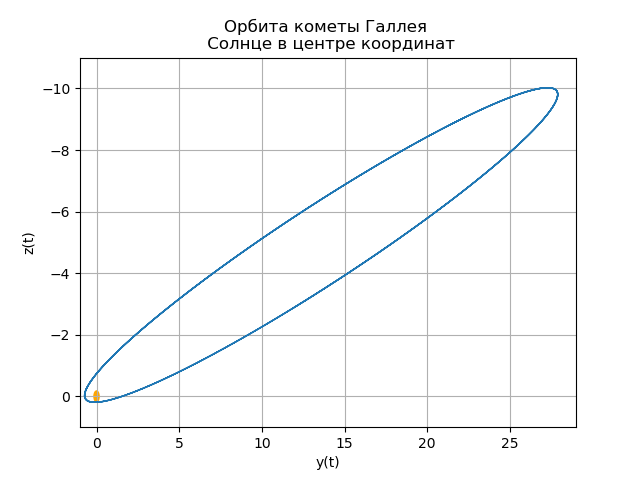
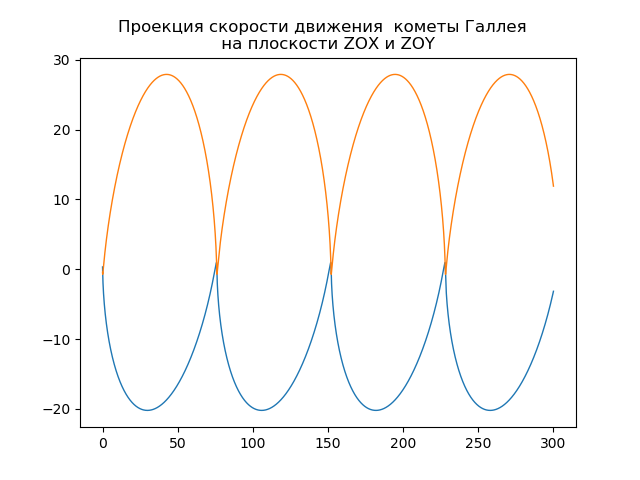المذنب الخاص بك

جرب تجربة. في الليل ، تقوم بتثبيت التلسكوب الخاص بك فوق تلة ليست بعيدة عن منزلك. يجب أن تكون الليل صافية وخالية من الغيوم ونجومية ، وإذا ابتسمت الثروة لك: في الساعة 0.30 صباحًا ستلاحظ مذنبًا جديدًا.

بعد الملاحظات المتكررة في الليالي التالية ، ستتمكن من حساب إحداثياتها في تلك الليلة الأولى. الإحداثيات في نظام إحداثيات مركزية الشمس: P0 = (x0، y0، z0) ومتجه السرعة v0 = (vx0، vy0، vz0).

باستخدام هذه البيانات ، حدد:

• مسافة المذنب من الشمس عند الحضيض (نقطة المدار الأقرب إلى الشمس) والأوج (نقطة المدار الأبعد عن الشمس) ؛
• سرعة المذنب عند المرور عبر الحضيض ومن خلال aphelion ؛
• فترة ثورة المذنب حول الشمس ؛
• التاريخان التاليان يمر المذنب من خلال الحضيض.

إذا قمنا بقياس المسافة في الوحدات الفلكية ، والوقت بالسنوات ، فستأخذ معادلة حركة المذنب الشكل (18). بالنسبة لمذنبك ، حدد إحداثيات وسرعات بدء تعسفية من نفس ترتيب مذنب هالي.

إذا لزم الأمر ، أعد إجراء اختيار تعسفي للموضع الأولي ومتجه السرعة حتى تحصل على مدار غريب الأطوار معقول يتجاوز مدار الأرض (مثل معظم المذنبات الحقيقية).

المراجع:

1. Feynman R. ، Leighton R. ، Sands M. Feynman Lectures in Physics. الطبعة الثالثة. T. 1.-2. م: مير ، 1977.
2. Matveev A.N. الميكانيكا ونظرية النسبية. م: العالي. مدرسة .1986.
3. الموسوعة الفيزيائية. T. 3. M: الموسوعة الروسية الكبيرة ، 1992.
4. دورة Landau L.D، Lifshits EM في الفيزياء النظرية. الميكانيكا. م: فو ماتجيز ، 1958.
5. Baskakov S.I. دوائر وإشارات الهندسة الراديوية. م: العالي. المدرسة .1988.
6. بورشنيف سي. محاكاة الكمبيوتر للعمليات الفيزيائية باستخدام حزمة mathcad .