العمل مع المصفوفات العددية بشكل عام وحل أنظمة المعادلات الجبرية الخطية على وجه الخصوص هو مشكلة رياضية وخوارزمية كلاسيكية تستخدم على نطاق واسع في نمذجة وحساب فئة ضخمة من العمليات التجارية (على سبيل المثال ، عند حساب التكلفة). عند إنشاء وتشغيل 1C: تكوينات المؤسسة ، واجه العديد من المطورين الحاجة إلى تنفيذ خوارزميات حساب SLAU يدويًا ، ثم مع مشكلة الانتظار الطويل للحصول على حل.
سيحتوي "1C: Enterprise" 8.3.14 على وظائف يمكنها تقليل الوقت المستغرق لحل أنظمة المعادلات الخطية بشكل كبير باستخدام خوارزمية تستند إلى نظرية الرسم البياني.
تم تحسينه للاستخدام على البيانات التي تحتوي على بنية متفرقة (أي لا تحتوي على ما لا يزيد عن 10 ٪ من المعاملات غير الصفرية في المعادلات) ، وفي المتوسط وفي أفضل الحالات ، توضح الخطوط المقاربة (n⋅log (n) ⋅log (n)) ، حيث n عدد المتغيرات ، وفي أسوأ الحالات (عندما يكون النظام ممتلئًا بنسبة 100 ٪ تقريبًا) ، فإن سلوكه المقارب يمكن مقارنته بالخوارزميات الكلاسيكية (Θ (n
3 )). علاوة على ذلك ، على الأنظمة ذات ~ 10
5 غير معروفة ، تظهر الخوارزمية تسارعًا مئات المرات مقارنة بتلك التي تم تنفيذها في مكتبات الجبر الخطي المتخصصة (على سبيل المثال ،
superlu أو
lapack ).
هام: تتطلب المقالة والخوارزمية الموصوفة فهمًا للجبر الخطي ونظرية الرسم البياني على مستوى السنة الأولى من الجامعة.عرض SLAE كرسم بياني
النظر في أبسط نظام متناثر من المعادلات الخطية:
تنبيه: يتم إنشاء النظام بشكل عشوائي وسيتم استخدامه لاحقًا لتوضيح خطوات الخوارزميةللوهلة الأولى ، ينشأ ارتباط مع كائن رياضي آخر - مصفوفة مجاورة الرسم البياني. فلماذا لا يتم تحويل البيانات إلى قوائم متجاورة ، وتوفير ذاكرة الوصول العشوائي في وقت التشغيل وتسريع الوصول إلى المعاملات غير الصفرية؟
للقيام بذلك ، يكفي تبديل المصفوفة وإنشاء
المتغير الثابت
"A [i] [j] = z ⇔ المتغير i-th يدخل المعادلة j مع المعامل z" ، ومن ثم بالنسبة لأي غير صفري A [i] [j] قم ببناء الحافة المقابلة من القمة i إلى القمة j.
سيبدو الرسم البياني الناتج كما يلي:
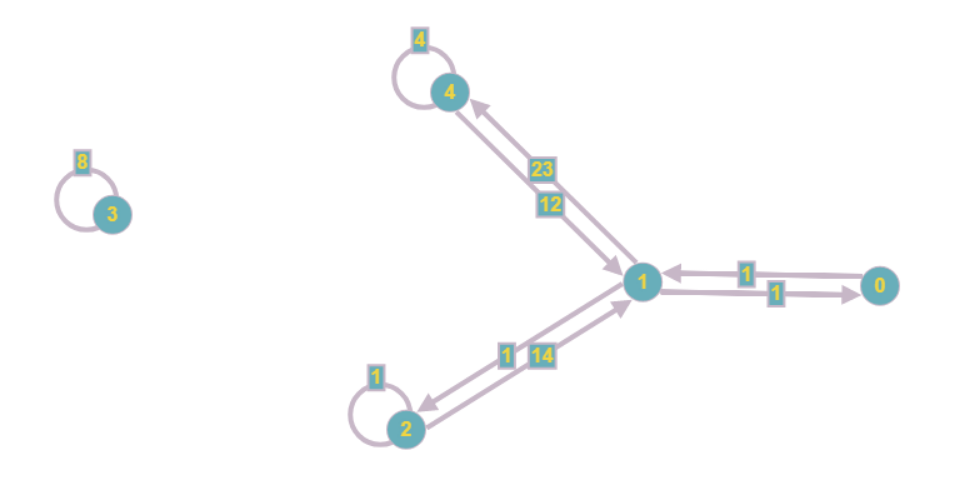
حتى بصريا ، اتضح أنها أقل تعقيدًا ، وتقل تكاليف الذاكرة المقاربة من O (n
2 ) إلى O (n + m) ، حيث m هو عدد المعاملات في النظام.
عزل المكونات ضعيفة الاتصال
الفكرة الخوارزمية الثانية التي تتبادر إلى الذهن عند النظر في الكيان الناتج: استخدام مبدأ "فرق تسد". من حيث الرسم البياني ، يؤدي ذلك إلى فصل مجموعة القمم إلى مكونات ضعيفة الاتصال.
دعني أذكرك بأن المكون ضعيف الاتصال هو مجموعة فرعية من القمم تكون قصوى في التضمين بين أي اثنين يوجد مسار من الحواف في رسم بياني غير موجه. يمكننا الحصول على رسم بياني غير موجه من الرسم الأصلي ، على سبيل المثال ، عن طريق إضافة العكس لكل حافة (مع الإزالة اللاحقة). ثم سيشمل رأس اتصال واحد جميع القمم التي يمكننا الوصول إليها عندما نذهب حول الرسم البياني بعمق.
بعد فصل المكونات الضعيفة ، سيأخذ الرسم البياني الشكل التالي:
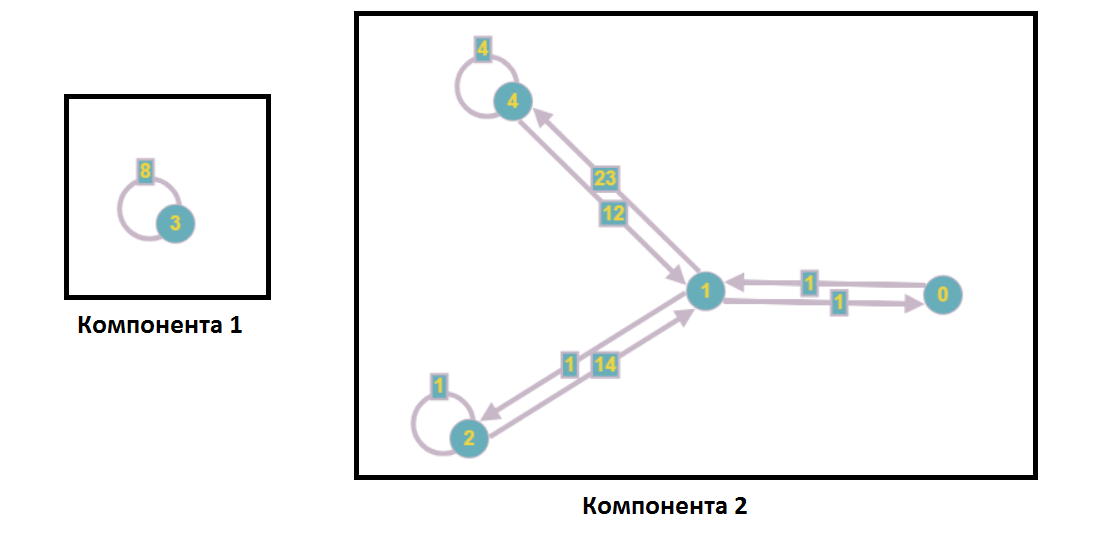
كجزء من تحليل نظام المعادلات الخطية ، هذا يعني أنه لا يتم تضمين قمة الرأس من المكون الأول في المعادلات مع أرقام المكون الثاني والعكس بالعكس ، أي أنه يمكننا حل هذه النظم الفرعية بشكل مستقل (على سبيل المثال ، بالتوازي).
رسم بياني لتخفيض القمة
الخطوة التالية من الخوارزمية هي بالضبط ما هو التحسين للعمل مع المصفوفات المتفرقة. حتى في الرسم البياني من المثال توجد قمم "معلقة" ، مما يعني أن بعض المعادلات تتضمن فقط واحدة غير معروفة ، وكما نعلم ، من السهل العثور على قيمة هذا المجهول.
لتحديد مثل هذه المعادلات ، يُقترح تخزين مجموعة من القوائم التي تحتوي على عدد المتغيرات المدرجة في المعادلة التي تحتوي على عدد عنصر الصفيف هذا. بعد ذلك ، عندما تصل القائمة إلى حجم الوحدة ، يمكننا تقليل قمة "فقط" ، وإبلاغ بقية المعادلات في المعادلات الأخرى التي يدخل فيها هذا الرأس.
وبالتالي ، يمكننا تقليل قمة الرأس 3 من المثال مباشرة بعد المعالجة الكاملة للمكون:
8⋅3=4⇒3=1/2
نمضي بالمثل بالمعادلة 0 ، لأنها تحتوي على متغير واحد فقط:
1⋅x1=1⇒x1=1
ستتغير المعادلات الأخرى أيضًا بعد العثور على هذه النتيجة:
$$ display $$ 1⋅_1 + 1⋅_2 = 3⇒1⋅_2 = 3-1 = 2 $$ display $$
يأخذ الرسم البياني الشكل التالي:
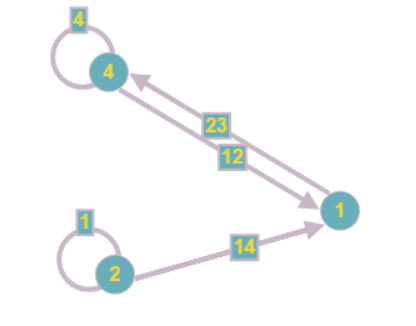
لاحظ أنه عند تقليل قمة واحدة ، قد يظهر البعض الآخر أيضًا يحتوي على رأس غير معروف. لذا يجب تكرار هذه الخطوة من الخوارزمية حتى يمكن تخفيض واحدة على الأقل من القمم.
إعادة الرسم البياني
يمكن للقراء الأكثر انتباهاً أن يلاحظوا أن الموقف ممكن حيث يكون لكل من رؤوس الرسم البياني درجة حدوث لا تقل عن اثنين وسيكون من المستحيل الاستمرار في تقليل القمم باستمرار.
أبسط مثال على مثل هذا الرسم البياني: لكل قمة درجة حدوث تساوي درجتين ، ولا يمكن تقليل أي من القمم.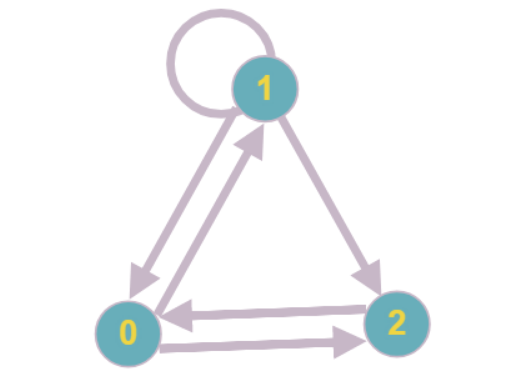
كجزء من التحسين للمصفوفات المتفرقة ، من المفترض أن مثل هذه المخططات الفرعية ستكون صغيرة الحجم ، ومع ذلك ، لا يزال عليك العمل معهم. لحساب قيم المجهول التي هي جزء من النظام الفرعي للمعادلات ، يُقترح استخدام الطرق الكلاسيكية لحل SLAEs (وهذا هو السبب في أن المقدمة تشير إلى أنه بالنسبة للمصفوفة التي تكون فيها جميع المعاملات أو كلها تقريبًا في المعادلات غير صفرية ، فإن الخوارزمية لدينا سيكون لها نفس التعقيد المقارب مثل المعادلات القياسية )
على سبيل المثال ، يمكنك إعادة مجموعة القمم المتبقية بعد التخفيض إلى نموذج المصفوفة وتطبيق
طريقة Gauss لحل SLAEs عليها . وبالتالي ، سوف نحصل على الحل الدقيق ، وستنخفض سرعة الخوارزمية نظرًا لعدم معالجة النظام بأكمله ، ولكن جزءًا منه فقط.
اختبار الخوارزمية
لاختبار تنفيذ البرنامج للخوارزمية ، أخذنا العديد من الأنظمة الحقيقية لمعادلات الحجم الكبير ، بالإضافة إلى عدد كبير من الأنظمة التي تم إنشاؤها عشوائيًا.
مرّ نظام المعادلات العشوائية من خلال الإضافة التسلسلية لحواف الوزن التعسفي بين ذروتين عشوائيتين. في المجموع ، كان النظام ممتلئًا بنسبة 5-10٪. تم التحقق من صحة الحلول عن طريق استبدال الإجابات التي تم الحصول عليها في نظام المعادلات الأصلي.
تراوحت الأنظمة من 1000 إلى 200000 مجهولةلمقارنة الأداء ، استخدمنا المكتبات الأكثر شيوعًا لحل مشكلات الجبر الخطي ، مثل superlu و lapack. بالطبع ، تركز هذه المكتبات على حل فئة واسعة من المشاكل ولا يتم تحسين حل SLAE فيها بأي شكل من الأشكال ، لذلك تبين أن الفرق في السرعة كبير.
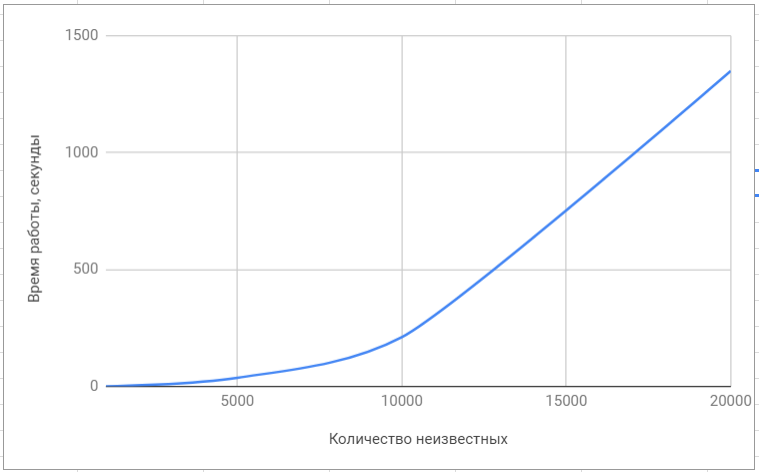اختبار مكتبة لاباك
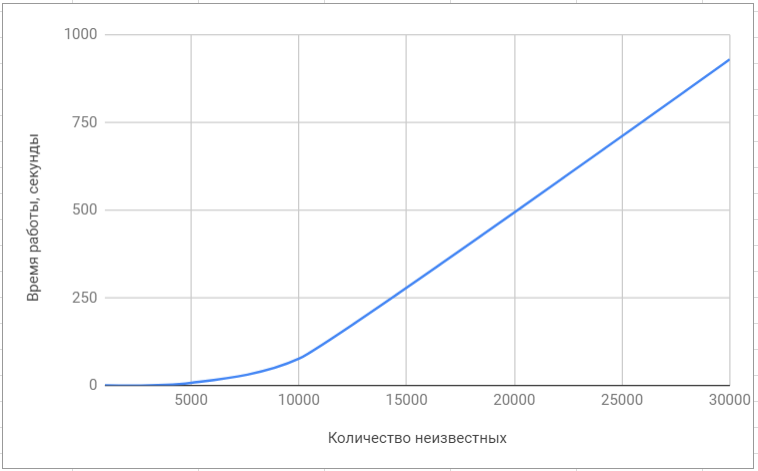اختبار مكتبة "superlu"فيما يلي المقارنة النهائية للخوارزمية مع الخوارزميات المطبقة في المكتبات الشائعة:
الخلاصة
حتى إذا لم تكن مطورًا 1C: Enterprise ، يمكنك استخدام الأفكار وطرق التحسين الموضحة في هذه المقالة ليس فقط عند تنفيذ خوارزمية لحل SLAEs ، ولكن أيضًا لفئة كاملة من مشاكل الجبر الخطي المرتبطة بالمصفوفات.
بالنسبة لمطوري 1C ، نضيف أن الوظيفة الجديدة لحل SLAE تدعم الاستخدام المتوازي لموارد الحوسبة ، ويمكنك ضبط عدد سلاسل العمليات الحسابية المستخدمة.