"إن الهدف من هذه الدورة هو إعدادك لمستقبلك الفني."

يبقى نشر فصلين ...
النمذجة - III
سأستمر في التوجيه العام الوارد في الفصل السابق ، ولكن هذه المرة سأركز على التعبير القديم "القمامة داخل - القمامة خارج" ، والذي غالبًا ما يتم اختصاره كـ GIGO (القمامة في الداخل ، القمامة خارج). الفكرة هي أنه إذا قمت بوضع بيانات تم جمعها بشكل غير دقيق وتعبيرات محددة بشكل غير صحيح على الإدخال ، فإن الناتج يمكنك الحصول على نتائج غير صحيحة فقط. والعكس صحيح أيضًا: من توفر بيانات إدخال دقيقة ، يتم الحصول على النتيجة الصحيحة. سأثبت أن كلا هذين الافتراضين يمكن أن يكون خطأ.
غالبًا ما تستند النمذجة إلى حل المعادلات التفاضلية ، لذا فبالنسبة للمبتدئين ، سننظر في أبسط معادلة تفاضلية للترتيب الأول من النموذج
كما تتذكر ، مجال الاتجاه هو الخطوط التي تم إنشاؤها في كل نقطة من المستوى xy ، مع المعامل الزاوية التي قدمتها المعادلة التفاضلية (الشكل 20.I). على سبيل المثال ، المعادلة التفاضلية لها حقل اتجاه موضح في الشكل 20.II.
الشكل 20.Iلكل دائرة متحدة المركز ،
بحيث يكون منحدر الخط هو نفسه دائمًا ويعتمد على قيمة k. تسمى هذه المنحنيات
isoclines .
الآن دعونا نلقي نظرة على مجال الاتجاه لمعادلة تفاضلية أخرى (الشكل 20.III). على الجانب الأيسر نرى حقل اتجاهات متباينة ، مما يعني أن التغييرات الصغيرة في القيم الأولية أو أخطاء الحساب الصغيرة ستؤدي إلى اختلاف كبير في القيم في منتصف المسار. على الجانب الأيمن نرى أن مجال الاتجاه يتقارب. هذا يعني أنه مع وجود اختلاف أكبر في منتصف المسار ، سيكون الفرق في القيم في الطرف الأيمن صغيرًا. يوضح هذا المثال البسيط كيف يمكن أن تصبح الأخطاء الصغيرة كبيرة ، والأخطاء الكبيرة صغيرة ، وعلاوة على ذلك ، كيف يمكن أن تصبح الأخطاء الصغيرة كبيرة ثم صغيرة مرة أخرى. لذلك ، تعتمد دقة الحل على الفاصل الزمني المحدد الذي يتم فيه حساب الحل. لا توجد دقة عامة مطلقة.
الشكل 20.IIالشكل 20.IIIهذه الاعتبارات مبنية للوظيفة
وهو حل المعادلة التفاضلية
ربما تخيلت "ماسورة" تتوسع أولاً ثم تضيق حول "الحل الحقيقي والدقيق" للمعادلة. هذا التمثيل مثالي لحالة قياسين ، ولكن عندما يكون لدي نظام من هذه المعادلات التفاضلية - 28 في حالة مشكلة الصواريخ الاعتراضية للبحرية المذكورة سابقًا - فإن هذه "الأنابيب" حول الحل الحقيقي للمعادلة تتضح أنها ليست كما تبدو للوهلة الأولى. يؤدي الشكل الذي يتكون من أربع دوائر في بعدين إلى مفارقة الأبعاد n للمساحة العشرية الأبعاد الموصوفة في الفصل 9. هذه مجرد وجهة نظر أخرى لمشكلة النمذجة المستقرة وغير المستقرة ، الموصوفة في الفصل السابق. هذه المرة سأقدم أمثلة محددة تتعلق بالمعادلات التفاضلية.
كيف نحل المعادلات التفاضلية عدديا؟ بدءًا من المعادلة التفاضلية من الدرجة الأولى المعتادة ، نرسم مجالًا للاتجاهات. مهمتنا هي الحصول على قيمة أولية معينة لحساب القيمة في أقرب نقطة تالية تهمنا. إذا أخذنا معامل المنحدر المحلي للخط الذي قدمته المعادلة التفاضلية واتخذنا خطوة صغيرة إلى الأمام على طول المماس ، فسوف نقدم خطأ صغيرًا فقط (الشكل 20.IV).
باستخدام هذه النقطة الجديدة ، سننتقل إلى النقطة التالية ، ولكن كما يتبين من الشكل ، فإننا ننحرف تدريجيًا عن المنحنى الحقيقي ، لأننا نستخدم معامل الميل للخطوة السابقة ، وليس معامل الميل الحقيقي للفاصل الحالي. لتجنب هذا التأثير ، "نتنبأ" بقيمة معينة ، ثم نستخدمها لتقدير المعامل الزاوية عند هذه النقطة (باستخدام المعادلة التفاضلية) ، ثم استخدام متوسط قيمة المعامل الزاوي عند حدود الفاصل الزمني كمعامل الزاوية لهذا الفاصل الزمني.
ثم ، باستخدام هذا المنحدر المتوسط ، نأخذه خطوة أخرى إلى الأمام ، هذه المرة باستخدام صيغة "التصحيح". إذا كانت القيم التي تم الحصول عليها باستخدام صيغتي "التنبؤ" و "التصحيح" قريبة بما فيه الكفاية ، فإننا نفترض أن حساباتنا دقيقة بما يكفي ، وإلا يجب علينا تقليل حجم الخطوة. إذا كان الفرق بين القيم صغيرًا جدًا ، فيجب علينا زيادة حجم الخطوة. وبالتالي ، فإن مخطط مصحح التنبؤ التقليدي لديه آلية مدمجة للتحقق من الأخطاء في كل خطوة ، ولكن هذا الخطأ في خطوة معينة ليس بأي حال من الأحوال ولا يوجد خطأ متراكم شائع! من الواضح تمامًا أن الخطأ المتراكم يعتمد على ما إذا كان مجال الاتجاه متقاربًا أم متباعدًا.
الشكل 20.IVالشكل 20.Vاستخدمنا خطوطًا مستقيمة بسيطة لكل من خطوة التنبؤ وخطوة التصحيح. استخدام كثيرات الحدود من درجات أعلى يعطي نتيجة أكثر دقة ؛ عادة ما يتم استخدام كثيرات الحدود من ربع درجة (حل المعادلات التفاضلية بطريقة Adams-Bashfort ، طريقة Milne ، طريقة Hamming ، إلخ). وبالتالي ، يجب علينا استخدام قيم الدالة ومشتقاتها في عدة نقاط سابقة للتنبؤ بقيمة الدالة عند النقطة التالية ، وبعد ذلك نستخدم استبدال هذه القيمة في المعادلة التفاضلية وتقريب القيمة الجديدة للمعامل الزاوي. باستخدام القيم الجديدة والسابقة للمعامل الزاوية وكذلك قيم الدالة المطلوبة ، نقوم بتصحيح القيمة التي تم الحصول عليها. حان الوقت لملاحظة أن المصحح ليس أكثر من مرشح رقمي تكراري تكون فيه قيم المدخلات مشتقات وقيم المخرجات هي قيم الوظيفة المطلوبة.
الاستقرار والمفاهيم الأخرى التي نوقشت في وقت سابق لا تزال ذات صلة. كما ذكرنا سابقًا ، هناك حلقة تغذية مرتدة إضافية للحل المتوقع للمعادلة التفاضلية ، والتي تستخدم بدورها في حساب المعامل الزاوية المعدلة. يتم استخدام كل من هذه القيم في حل المعادلة التفاضلية ، والمرشحات الرقمية العودية ليست سوى صيغ ، وليس أكثر. ومع ذلك ، فهي ليست خصائص نقل ، لأنها تعتبر عادة في نظرية المرشحات الرقمية. في هذه الحالة ، يتم حساب قيم المعادلة التفاضلية ببساطة. في هذه الحالة ، يكون الفرق بين المقاربات مهمًا: في المرشحات الرقمية ، تتم معالجة الإشارة بشكل خطي ، بينما في حل المعادلات التفاضلية ، هناك اللاخطية ، التي يتم تقديمها عن طريق حساب قيم مشتقات الدالة. هذا ليس هو نفس المرشح الرقمي.
إذا قمت بحل نظام من المعادلات التفاضلية n ، فأنت تتعامل مع ناقل للمكونات n. يمكنك توقع القيمة التالية لكل مكون ، وتقييم كل من المشتقات n ، وضبط كل من القيم المتوقعة ، ثم قبول نتيجة الحساب في هذه الخطوة أو رفضها إذا كان الخطأ المحلي كبيرًا جدًا. تميل إلى التفكير في الأخطاء الصغيرة على أنها "قناة" تحيط بمسار محسوب حقيقي. ومرة أخرى ، أحثك على تذكر مفارقة الدوائر الأربع في المساحات عالية الأبعاد. قد لا تكون هذه "الأنابيب" كما تبدو للوهلة الأولى.
دعوني الآن أشير إلى الاختلاف الهام بين النهجين: الطرق الحسابية ونظرية المرشحات الرقمية. في الكتب المدرسية الشائعة ، يتم وصف طرق الرياضيات الحسابية فقط التي تقارب الدوال التي كتبها كثيرات الحدود. تستخدم المرشحات العودية الترددات في صيغ التقييم! هذا يؤدي إلى اختلافات كبيرة!
لمعرفة الفرق ، دعنا نتخيل أننا نقوم بتطوير جهاز محاكاة لهبوط الإنسان على كوكب المريخ. يركز النهج الكلاسيكي على شكل مسار الهبوط ويستخدم تقريب كثير الحدود للمناطق المحلية. سيكون للمسار الناتج نقاط كسر في التسارع ، حيث نتحرك خطوة بخطوة من فترة إلى أخرى. في حالة نهج التردد ، سوف نركز على الحصول على الترددات الصحيحة ونترك الموقع كما هو. في الحالة المثالية ، سيكون كلا المسارين متشابهين ، ولكن من الناحية العملية يمكن أن يختلفا بشكل كبير.
أي نزهة يجب أن أستخدمها؟ كلما فكرت في الأمر أكثر ، كلما كنت تميل إلى الاعتقاد بأن الطيار في المحاكي يريد الحصول على "إحساس" بسلوك وحدة الهبوط ، ويبدو أن استجابة التردد للمحاكاة يجب أن يشعر بها الطيار جيدًا. إذا كان الموقع مختلفًا قليلاً ، فإن حلقة التغذية المرتدة ستعوض عن هذا الانحراف أثناء عملية الهبوط ، ولكن إذا اختلف "شعور" التحكم أثناء الرحلة الحقيقية ، فسيكون الطيار قلقًا بشأن "الأحاسيس" الجديدة التي لم تكن موجودة في جهاز المحاكاة. بدا لي دائمًا أنه يجب على المحاكيات إعداد تجريب لأحاسيس حقيقية قدر الإمكان (بالطبع ، لا يمكننا محاكاة الجاذبية المنخفضة على كوكب المريخ لفترة طويلة) ، بحيث يشعرون بالراحة عندما يواجهون في الواقع موقفًا يواجهون فيه واجهت مرارا وتكرارا في المحاكي. للأسف ، نحن لا نعرف إلا القليل عما يشعر به الطيار. هل يشعر الطيار فقط بالترددات الفعلية من توسع فورييه ، أم أنه يشعر أيضًا بترددات لابلاس المعقدة (أو ربما يجب علينا استخدام الموجات؟). هل يشعر الطيارون المختلفون بنفس الأشياء؟ نحن بحاجة إلى معرفة أكثر مما نعرفه الآن عن شروط التصميم الأساسية هذه.
الموقف الموصوف أعلاه هو تناقض قياسي بين النهج الرياضي والهندسي لحل المشكلة. هذه الأساليب لها أهداف مختلفة في حل المعادلات التفاضلية (كما هو الحال في العديد من المشاكل الأخرى) ، وبالتالي فهي تؤدي إلى نتائج مختلفة. إذا توصلت إلى النمذجة ، سترى أن هناك فروق دقيقة مخفية تبين أنها مهمة جدًا في الممارسة ، ولكن أي علماء الرياضيات لا يعرفون شيئًا وسوف ينكرون في كل شيء عواقب إهمالهم. دعونا نلقي نظرة على مسارين (الشكل 20.IV) ، والذي قدرته تقريبًا. يصف المنحنى العلوي الموقع بشكل أكثر دقة ، ولكن الانحناءات تعطي "إحساسًا" مختلفًا تمامًا مقارنة بالعالم الحقيقي ، والمنحنى الثاني أكثر خطأ في الموقع ، ولكن لديه دقة أكبر من حيث "الإحساس". لقد أوضحت مرة أخرى بوضوح لماذا أعتقد أن الشخص الذي لديه فهم عميق لموضوع المشكلة يجب أن يفهم أيضًا الطرق الرياضية لحلها ، ولا يعتمد على الطرق التقليدية للحل.
أريد الآن أن أروي قصة أخرى عن الأيام الأولى لاختبار نظام Nike للدفاع الصاروخي. في ذلك الوقت ، كانت تجري التجارب الميدانية في White Sands ، والتي كانت تسمى أيضًا "اختبار الهاتف الميداني". كانت هذه عمليات إطلاق اختبار اضطر فيها الصاروخ إلى اتباع مسار محدد مسبقًا وانفجر في اللحظة الأخيرة ، بحيث لا تتجاوز كل طاقة الانفجار منطقة معينة وتسبب المزيد من الضرر ، وهو ما يفضل على انخفاض أخف في الأجزاء الفردية من الصاروخ على الأرض ، والتي من المفترض أنه كان يجب أن يكون أقل ضررًا. كان الهدف من الاختبارات هو الحصول على قياسات حقيقية للرفع والسحب كدالة لارتفاع وسرعة الرحلة من أجل تصحيح وتحسين التصميم.
عندما التقيت بصديقي الذي عاد من الاختبار ، تجول في ممرات مختبرات بيل وبدا حزينًا إلى حد ما. لماذا؟ لأن أول اثنتين من عمليات الإطلاق الستة المقررة فشلت في منتصف الرحلة ولم يعرف أحد السبب. لم تكن البيانات اللازمة لمراحل التصميم الإضافية متاحة ، مما يعني مشاكل خطيرة للمشروع بأكمله. قلت أنه إذا كان يستطيع أن يقدم لي معادلات تفاضلية تصف الرحلة ، فيمكنني أن أضع الفتاة لحلها (لم يكن الوصول إلى أجهزة الكمبيوتر الكبيرة في أواخر الأربعينيات أمرًا سهلاً). بعد حوالي أسبوع ، قدموا سبع معادلات تفاضلية من الدرجة الأولى وكانت الفتاة جاهزة للبدء. ولكن ما هي الشروط الأولية قبل لحظة من بدء مشاكل الطيران؟ (في تلك الأيام ، لم تكن لدينا قوة حوسبة كافية لحساب مسار الرحلة بالكامل بسرعة.) لم يعرفوا! كانت بيانات القياس عن بعد غير مفهومة قبل لحظة من الفشل. لم أتفاجأ ولم يزعجني ذلك. لذلك ، استخدمنا القيم التقديرية للارتفاع وسرعة الطيران وزاوية الهجوم وما إلى ذلك. - حالة أولية واحدة لكل من المتغيرات التي تصف مسار الرحلة. وبعبارة أخرى ، كان لدي قمامة عند المدخل. لكنني أدركت في وقت سابق أن طبيعة الاختبارات الميدانية التي قمنا بمحاكاةها كانت بمثابة تصحيح تلقائي للانحرافات الصغيرة عن المسار المقترح بواسطة نظام التوجيه! كنت أتعامل مع مجال اتجاهات متقارب للغاية.
وجدنا أن الصاروخ كان مستقرًا على طول المحاور المستعرضة والرأسية ، ولكن عندما استقر أحدهما ، أدت زيادة الطاقة إلى تذبذبات على طول المحور الآخر. وبالتالي ، لم يكن هناك فقط تذبذبات على طول المحاور المستعرضة والرأسية ، ولكن أيضًا انتقال دوري للطاقة المتزايدة بينهما ، بسبب دوران الصاروخ حول محوره الطولي. بمجرد أن تم توضيح المنحنيات المحسوبة لجزء صغير من المسار ، أدرك الجميع على الفور أن الاستقرار المتقاطع لم يؤخذ في الاعتبار ، وكان الجميع يعرف كيفية إصلاحه. لذا ، حصلنا على حل سمح لنا أيضًا بقراءة بيانات القياس عن بعد الفاسدة التي تم الحصول عليها أثناء الاختبارات ، ولتوضيح فترة نقل الطاقة - في الواقع ، قدم المعادلات التفاضلية الصحيحة للحسابات. كان لدي القليل من العمل ، باستثناء التأكد من أن الفتاة التي لديها آلة حاسبة سطح المكتب تحسب كل شيء بصدق. لذلك ، في شهر مايو ، كان الجدارة في فهم أنه (1) يمكننا محاكاة ما حدث (الآن هو روتين في التحقيق في الحوادث ، ولكن بعد ذلك كان ابتكارًا) و (2) يتقارب مجال الاتجاه ، لذلك قد لا يتم تحديد الشروط الأولية بالضبط.
أخبرتك هذه القصة من أجل إظهار أن مبدأ GIGO لا يعمل دائمًا. حدثت لي قصة مشابهة أثناء محاكاة قنابل مبكرة في لوس ألاموس. تدريجيا ، توصلت إلى فهم أن حساباتنا ، التي بنيت لمعادلة الدولة ، كانت تستند إلى بيانات غير دقيقة إلى حد ما. ترتبط معادلة الحالة بضغط وكثافة المادة (درجة الحرارة أيضًا ، ولكن سأحذفها في هذا المثال). تم تصوير البيانات من مختبرات الضغط العالي ، والتقريبات التي تم الحصول عليها من دراسة الزلازل ، وكثافة النواة النجمية والنظرية المقاربة للضغوط اللانهائية كنقاط على ورقة رسم بياني كبيرة جدًا (الشكل 20.VII). ثم ، باستخدام الأنماط ، رسمنا منحنيات تربط النقاط المتناثرة. بعد ذلك ، وبناءً على هذه المنحنيات ، قمنا ببناء جداول قيم الدوال بدقة 3 منازل عشرية. هذا يعني أننا افترضنا ببساطة 0 أو 5 في العلامة العشرية الرابعة. استخدمنا هذه البيانات لبناء جداول حتى المنازل العشرية الخامسة والسادسة. بناءً على هذه الجداول ، تم إنشاء حساباتنا الإضافية. في ذلك الوقت ، كما ذكرت سابقًا ، كنت نوعًا من الآلات الحاسبة ، وكانت وظيفتي هي العد وبالتالي تحرير الفيزيائيين من هذه المهنة ، للسماح لهم بالقيام بعملهم.
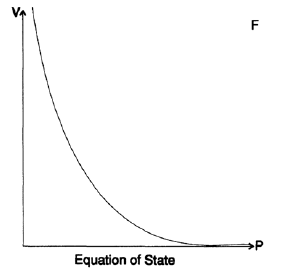
بعد انتهاء الحرب ، بقيت في لوس ألاموس لمدة نصف عام آخر ، وكان أحد أسباب ذلك هو أنني أردت أن أفهم كيف يمكن لهذه البيانات غير الدقيقة أن تؤدي إلى مثل هذه المحاكاة الدقيقة للتصميم النهائي. فكرت في هذا لفترة طويلة ، ووجدت الجواب. في منتصف الحسابات ، استخدمنا اختلافات محدودة من الدرجة الثانية. أظهر الاختلاف من الدرجة الأولى قيمة القوة على جانب واحد من كل قذيفة ، وأعطت الاختلافات في الأصداف المجاورة على كلا الجانبين القوة الناتجة ، والتي تحرك القشرة. اضطررنا لاستخدام الأصداف الرفيعة ، لذلك قمنا بطرح أرقام قريبة جدًا من بعضنا البعض ، وكنا بحاجة إلى استخدام العديد من الأرقام بعد الفاصلة العشرية. أظهرت دراسات أخرى أنه عندما انفجر "الشيء" ، تحركت القشرة لأعلى على طول المنحنى ، وربما في بعض الأحيان انحسرت جزئيًا إلى الخلف ، لذلك كان أي خطأ محلي في معادلة الحالة قريبًا من متوسط القيمة. كان من المهم حقًا الحصول على انحناء معادلة الحالة ، وكما ذكرنا سابقًا ، كان يجب أن تكون دقيقة في المتوسط. وهكذا ، القمامة في المدخلات ، ولكن نتائج أكثر دقة من أي وقت مضى الإخراج!
توضح هذه الأمثلة الثلاثة ما تم ذكره ضمنيًا سابقًا - إذا كان هناك حلقة تغذية راجعة للمتغيرات المستخدمة في المشكلة ، فليس من الضروري معرفة قيمها بدقة. وبناءً على ذلك ، فإن فكرة GS Black الرائعة حول كيفية بناء حلقة تغذية مرتدة في مضخمات الصوت (الشكل 20.VIII): طالما أن الكسب مرتفع جدًا ، يجب فقط مطابقة مقاومة المقاوم بدقة ، ويمكن لجميع الأجزاء الأخرى أن يتم تنفيذها بدقة منخفضة. بالنسبة للدائرة الموضحة في الشكل 20.VIII نحصل على التعبيرات التالية:
20.VIII, 1/10, . .
, , . , . , , ? , .
, ! . . , , , . , . , « » .
, .
, , 20.IX
.
y -
x , sinh(
y ) , , . ,
y , . , . , , : . , , .
20.IX, , , , k. , - . , , , , , , . , , .
, , . , , - . , .
, , . , , , , , , . , , , , , , . , — , . , , , , - , . , , , , .
, , . , , , . , , . «» . , , . , . , , - , . , .
. , - , 12 — . , , . , 20 , , . , 20 , . . , .
, , ! , ( ) , . , — . , !
. , , , . : , , - , !
. : « , , ?». , . — «» «», «» «» . 90% , 10 , ,
. : , ( ) , ( ). , 95%, . — , . « » — .
, — . : « , . . , ».
? - , ? , , « , ». , , .
, , ? , . , , , , , , , . , . , , , , , , , , . — , , , , . . , , . , ? , ? .
19 , , ? . , , . , , , , . , , « … ?». 18 , , , — , , .
« … ?», , , , . , , . , , — , - . , . , .
« … ?» , , , .
..., — magisterludi2016@yandex.ru, —
«The Dream Machine: » )