
أعتقد أن القليل من الهراء يوم الثلاثاء لن يؤذي أسبوع العمل. لدي هواية ، في وقت فراغي أحاول معرفة كيفية اختراق خوارزمية تعدين البيتكوين ، وتجنب البحث الغبي غير المرئي وإيجاد حل لمشكلة مطابقة التجزئة مع الحد الأدنى من استهلاك الطاقة. يجب أن أقول على الفور النتيجة ، بالطبع لم أحققها بعد ، ولكن مع ذلك ، لماذا لا تطرح في كتابة الأفكار التي تولد في الرأس؟ في مكان ما يجب وضعهم ...
على الرغم من خداع الأفكار أدناه ، أعتقد أن هذه المقالة قد تكون مفيدة لشخص يدرس
- لغة C ++ وقوالبها
- بعض الدوائر الرقمية
- القليل من نظرية الاحتمالية والحساب الاحتمالي
- خوارزمية تجزئة البيتكوين بالتفصيل
من أين نبدأ؟
ربما من العنصر الأخير والأكثر مملة في هذه القائمة؟ الصبر ، سيكون أكثر متعة.
دعونا نفكر بالتفصيل في خوارزمية حساب وظيفة التجزئة لبيتكوين. وهو بسيط F (x) = sha256 (sha256 (x)) ، حيث x هو الإدخال 80 بايت ، رأس الكتلة مع رقم إصدار الكتلة ، تجزئة الكتلة السابقة ، جذر merkle ، الطابع الزمني ، البتات وغير المستقرة. فيما يلي أمثلة لرؤوس كتل حديثة إلى حد ما يتم تمريرها إلى وظيفة التجزئة:
تعتبر هذه المجموعة من وحدات البايت مادة قيمة للغاية ، حيث أنه ليس من السهل غالبًا على عمال المناجم فهم الترتيب الذي يجب أن تتبعه وحدات البايت عند تشكيل الرأس ، مما يؤدي في كثير من الأحيان إلى عكس أماكن وحدات البايت المنخفضة والعالية (النهاية).
لذا ، من رأس الكتلة ، 80 بايت تعتبر تجزئة sha256 ثم من النتيجة sha256 أخرى.
خوارزمية sha256 نفسها ، إذا نظرت إلى مصادر مختلفة ، تتكون عادة من أربع وظائف:
- sha256_init باطل (SHA256_CTX * ctx) ؛
- sha256_transform باطل (SHA256_CTX * ctx، const BYTE data []) ؛
- sha256_update باطل (SHA256_CTX * ctx، const BYTE data []، size_t len) ؛
- sha256_final باطل (SHA256_CTX * ctx ، تجزئة BYTE []) ؛
أول وظيفة يتم استدعاؤها عند حساب التجزئة هي sha256_init () ، والتي تستعيد بنية SHA256_CTX. لا يوجد شيء خاص هناك باستثناء ثمانية كلمات حالة 32 بت ، والتي تمتلئ في البداية بكلمات خاصة:
void sha256_init(SHA256_CTX *ctx) { ctx->datalen = 0; ctx->bitlen = 0; ctx->state[0] = 0x6a09e667; ctx->state[1] = 0xbb67ae85; ctx->state[2] = 0x3c6ef372; ctx->state[3] = 0xa54ff53a; ctx->state[4] = 0x510e527f; ctx->state[5] = 0x9b05688c; ctx->state[6] = 0x1f83d9ab; ctx->state[7] = 0x5be0cd19; }
لنفترض أن لدينا ملفًا يجب حساب تجزئةه. نقرأ الملف مع كتل ذات حجم تعسفي ونستدعي الدالة sha256_update () حيث نقوم بتمرير المؤشر إلى بيانات الكتلة وطول الكتلة. تجمع الدالة التجزئة في بنية SHA256_CTX في مصفوفة الحالة:
void sha256_update(SHA256_CTX *ctx, const BYTE data[], size_t len) { uint32_t i; for (i = 0; i < len; ++i) { ctx->data[ctx->datalen] = data[i]; ctx->datalen++; if (ctx->datalen == 64) { sha256_transform(ctx, ctx->data); ctx->bitlen += 512; ctx->datalen = 0; } } }
في حد ذاته ، يستدعي sha256_update () دالة حصان العمل sha256_transform () ، والتي تقبل بالفعل كتلًا بطول ثابت يبلغ 64 بايت:
#define ROTLEFT(a,b) (((a) << (b)) | ((a) >> (32-(b)))) #define ROTRIGHT(a,b) (((a) >> (b)) | ((a) << (32-(b)))) #define CH(x,y,z) (((x) & (y)) ^ (~(x) & (z))) #define MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z))) #define EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22)) #define EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25)) #define SIG0(x) (ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3)) #define SIG1(x) (ROTRIGHT(x,17) ^ ROTRIGHT(x,19) ^ ((x) >> 10)) /**************************** VARIABLES *****************************/ static const uint32_t k[64] = { 0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5, 0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174, 0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da, 0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967, 0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85, 0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,0xd192e819,0xd6990624,0xf40e3585,0x106aa070, 0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3, 0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2 }; /*********************** FUNCTION DEFINITIONS ***********************/ void sha256_transform(SHA256_CTX *ctx, const BYTE data[]) { uint32_t a, b, c, d, e, f, g, h, i, j, t1, t2, m[64]; for (i = 0, j = 0; i < 16; ++i, j += 4) m[i] = (data[j] << 24) | (data[j + 1] << 16) | (data[j + 2] << 8) | (data[j + 3]); for (; i < 64; ++i) m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16]; a = ctx->state[0]; b = ctx->state[1]; c = ctx->state[2]; d = ctx->state[3]; e = ctx->state[4]; f = ctx->state[5]; g = ctx->state[6]; h = ctx->state[7]; for (i = 0; i < 64; ++i) { t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i]; t2 = EP0(a) + MAJ(a, b, c); h = g; g = f; f = e; e = d + t1; d = c; c = b; b = a; a = t1 + t2; } ctx->state[0] += a; ctx->state[1] += b; ctx->state[2] += c; ctx->state[3] += d; ctx->state[4] += e; ctx->state[5] += f; ctx->state[6] += g; ctx->state[7] += h; }
عندما تتم قراءة ملف التجزئة بالكامل ونقله بالفعل إلى الدالة sha256_update () ، كل ما تبقى هو استدعاء دالة sha256_final () النهائية ، والتي إذا لم يكن حجم الملف مضاعفًا لـ 64 بايت ، فسيضيف بايت إضافي للحشو ، ويكتب إجمالي طول البيانات في نهاية آخر كتلة بيانات و ستفعل sha256_transform () النهائي.
تبقى نتيجة التجزئة في صفيف الحالة.
هذا هو "المستوى العالي" إذا جاز التعبير.
فيما يتعلق بمنجم Bitcoin ، بالطبع ، يفكر المطورون في كيفية النظر إلى أصغر وأكثر كفاءة.
الأمر بسيط: يحتوي الرأس على 80 بايت فقط ، وهو ليس من مضاعفات 64 بايت. وبالتالي ، سيكون من الضروري أن تقوم sha256 الأولى بعمل sha256_transform () بالفعل. ومع ذلك ، لحسن الحظ بالنسبة لعمال المناجم ، فإن عدم وجود الكتلة في نهاية الرأس ، لذلك يمكن تنفيذ أول sha256_transform () مرة واحدة فقط - وهذا سيكون ما يسمى بالوسط. بعد ذلك ، يمر عامل المنجم بجميع الخيارات غير الموجودة ، والتي هي 4 مليارات ، 2 ^ 32 ويستبدلها في الحقل المقابل لـ sha256_transform () الثاني. يكمل هذا التحويل أول وظيفة sha256. والنتيجة هي ثماني كلمات 32 بت ، أي 32 بايت. من السهل العثور على sha256 منهم - يسمى sha256_transform () النهائي ، وكل شيء جاهز. لاحظ أن بيانات الإدخال أصغر بـ 32 بايت من 64 بايت المطلوبة لـ sha256_transform (). لذا مرة أخرى ، ستتم تعبئة الكتلة بالأصفار وسيتم إدخال طول الكتلة في النهاية.
إجمالاً ، هناك ثلاث مكالمات فقط لـ sha256_transform () يجب قراءة المكالمة الأولى مرة واحدة فقط لحساب الحالة الوسطى.
حاولت توسيع جميع عمليات معالجة البيانات التي تحدث عند حساب تجزئة رأس كتلة بيتكوين إلى دالة واحدة ، بحيث يكون من الواضح كيف يحدث الحساب بالكامل خصيصًا لبيتكوين وهذا ما حدث:
لقد قمت بتطبيق هذه الوظيفة كقالب c ++ ، يمكن أن تعمل ليس فقط على كلمات 32 بت ، على سبيل المثال uint32_t ، ولكن تعمل على كلمات من نوع مختلف "T" بنفس الطريقة. لدي هنا ويتم تخزين الحالة sha256 كمصفوفة من النوع "T" ويتم استدعاء sha256_transform () بمؤشر معلمة إلى صفيف من النوع "T" ويتم إرجاع النتيجة نفسها. أصبحت وظيفة التحويل الآن أيضًا في شكل قالب c ++:
template <typename T> T ror32(T word, unsigned int shift) { return (word >> shift) | (word << (32 - shift)); } template <typename T> T Ch(T x, T y, T z) { return z ^ (x & (y ^ z)); } template<typename T> T Maj(T x, T y, T z) { return (x & y) | (z & (x | y)); } #define e0(x) (ror32(x, 2) ^ ror32(x,13) ^ ror32(x,22)) #define e1(x) (ror32(x, 6) ^ ror32(x,11) ^ ror32(x,25)) #define s0(x) (ror32(x, 7) ^ ror32(x,18) ^ (x >> 3)) #define s1(x) (ror32(x,17) ^ ror32(x,19) ^ (x >> 10)) unsigned int ntohl(unsigned int in) { return ((in & 0xff) << 24) | ((in & 0xff00) << 8) | ((in & 0xff0000) >> 8) | ((in & 0xff000000) >> 24); } template <typename T> void LOAD_OP(int I, T *W, const u8 *input) { //W[I] = /*ntohl*/ (((u32*)(input))[I]); W[I] = ntohl(((u32*)(input))[I]); //W[I] = (input[3] << 24) | (input[2] << 16) | (input[1] << 8) | (input[0]); } template <typename T> void BLEND_OP(int I, T *W) { W[I] = s1(W[I - 2]) + W[I - 7] + s0(W[I - 15]) + W[I - 16]; } template <typename T> void sha256_transform(T *state, const T *input) { T a, b, c, d, e, f, g, h, t1, t2; TW[64]; int i; /* load the input */ for (i = 0; i < 16; i++) // MJ input is cast to u32* so this processes 16 DWORDS = 64 bytes W[i] = input[i]; /* now blend */ for (i = 16; i < 64; i++) BLEND_OP(i, W); /* load the state into our registers */ a = state[0]; b = state[1]; c = state[2]; d = state[3]; e = state[4]; f = state[5]; g = state[6]; h = state[7]; // t1 = h + e1(e) + Ch(e, f, g) + 0x428a2f98 + W[0]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x71374491 + W[1]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb5c0fbcf + W[2]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xe9b5dba5 + W[3]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x3956c25b + W[4]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x59f111f1 + W[5]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x923f82a4 + W[6]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xab1c5ed5 + W[7]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xd807aa98 + W[8]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x12835b01 + W[9]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x243185be + W[10]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x550c7dc3 + W[11]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x72be5d74 + W[12]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x80deb1fe + W[13]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x9bdc06a7 + W[14]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc19bf174 + W[15]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xe49b69c1 + W[16]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xefbe4786 + W[17]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x0fc19dc6 + W[18]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x240ca1cc + W[19]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x2de92c6f + W[20]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4a7484aa + W[21]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5cb0a9dc + W[22]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x76f988da + W[23]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x983e5152 + W[24]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa831c66d + W[25]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb00327c8 + W[26]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xbf597fc7 + W[27]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xc6e00bf3 + W[28]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd5a79147 + W[29]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x06ca6351 + W[30]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x14292967 + W[31]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x27b70a85 + W[32]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x2e1b2138 + W[33]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x4d2c6dfc + W[34]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x53380d13 + W[35]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x650a7354 + W[36]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x766a0abb + W[37]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x81c2c92e + W[38]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x92722c85 + W[39]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xa2bfe8a1 + W[40]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa81a664b + W[41]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xc24b8b70 + W[42]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xc76c51a3 + W[43]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xd192e819 + W[44]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd6990624 + W[45]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xf40e3585 + W[46]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x106aa070 + W[47]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x19a4c116 + W[48]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x1e376c08 + W[49]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x2748774c + W[50]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x34b0bcb5 + W[51]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x391c0cb3 + W[52]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4ed8aa4a + W[53]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5b9cca4f + W[54]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x682e6ff3 + W[55]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x748f82ee + W[56]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x78a5636f + W[57]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x84c87814 + W[58]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x8cc70208 + W[59]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x90befffa + W[60]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xa4506ceb + W[61]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xbef9a3f7 + W[62]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc67178f2 + W[63]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; state[0] += a; state[1] += b; state[2] += c; state[3] += d; state[4] += e; state[5] += f; state[6] += g; state[7] += h; }
يعد استخدام وظائف قالب C ++ مناسبًا حيث يمكنني حساب التجزئة التي أحتاجها من البيانات العادية والحصول على النتيجة المعتادة:
const uint8_t header[] = { 0x02,0x00,0x00,0x00, 0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7, 0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55, 0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17, 0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1, 0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44, 0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a, 0x19,0xc8,0xe6,0xba, 0xdc,0x14,0x17,0x87, 0x35,0x8b,0x05,0x53, 0x53,0x5f,0x01,0x19, 0x48,0x75,0x08,0x33 }; uint32_t test_nonce = 0x48750833; uint32_t result[8]; full_btc_hash(header, test_nonce, result); uint8_t* presult = (uint8_t * )result; for (int i = 0; i < 32; i++) printf("%02X ", presult[i]);
اتضح:
92 98 2A 50 91 FA BD 42 97 8A A5 2D CD C9 36 28 02 4A DD FE E0 67 A4 78 00 00 00 00 00 00 00 00 00
في نهاية التجزئة هناك العديد من الأصفار ، التجزئة الجميلة ، البنغو ، إلخ.
والآن أبعد من ذلك ، لا يمكنني تمرير بيانات uint32_t العادية إلى وظيفة التجزئة هذه ، ولكن فئة C ++ الخاصة بي ، والتي ستعيد تعريف جميع العمليات الحسابية.
نعم نعم. سأقوم بتطبيق الرياضيات الاحتمالية "البديلة".
اخترعت بنفسي ، أدركت ذلك ، جربته بنفسي. لا يبدو أنه يعمل بشكل جيد للغاية. مزحة. يجب أن تعمل. ربما لست أول من أحاول التدوير.
الآن ننتقل إلى الأكثر إثارة للاهتمام.
يتم تنفيذ جميع العمليات الحسابية في الإلكترونيات الرقمية كعمليات على البتات ، ويتم تعريفها بدقة من خلال العمليات و ، أو ، أو لا ، حصريًا أو. حسنًا ، نعلم جميعًا ما هي جداول الحقيقة الموجودة في الجبر البولياني.
أقترح إضافة القليل من عدم اليقين إلى الحسابات ، مما يجعلها احتمالية.
دع كل بت في الكلمة ليس فقط القيمتين صفر و ONE ، ولكن أيضًا جميع القيم الوسيطة! أقترح النظر في قيمة البت كاحتمال لحدث قد يحدث أو لا يحدث. إذا كانت جميع البيانات الأولية معروفة بشكل موثوق ، فإن النتيجة موثوقة. وإذا كانت بعض البيانات ناقصة قليلاً ، فستظهر النتيجة مع بعض الاحتمال.
في الواقع ، لنفترض أن هناك حدثان مستقلان "a" و "b" ، يكون احتمال حدوثهما بشكل طبيعي من صفر إلى واحد ، على التوالي ، Pa و Pb. ما هو احتمال وقوع الأحداث في وقت واحد؟ أنا متأكد من أن كل واحد منا لن يتردد في الإجابة P = Pa * Pb وهذه هي الإجابة الصحيحة!
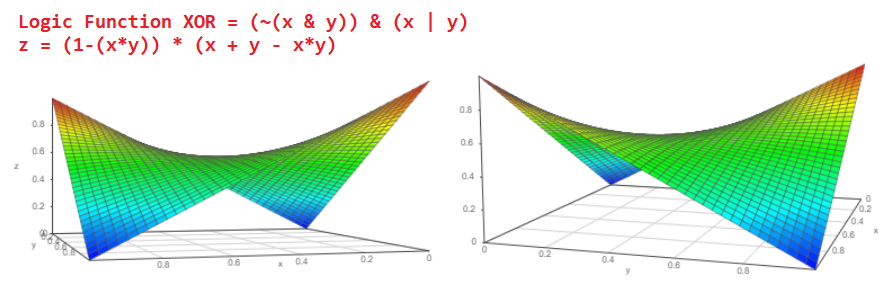
سيبدو الرسم البياني ثلاثي الأبعاد لهذه الوظيفة بهذا الشكل (من وجهتي نظر مختلفتين):
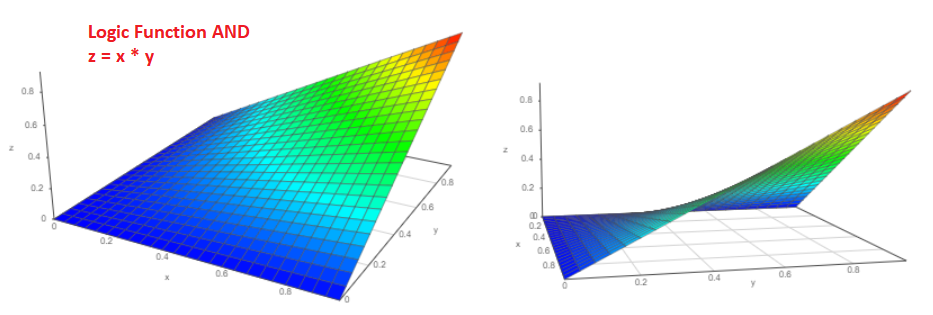
وما هو احتمال حدوث حدث Pa أو حدث Pb؟
الاحتمال P = Pa + Pb-Pa * Pb. الرسم البياني للدالة هو مثل هذا:
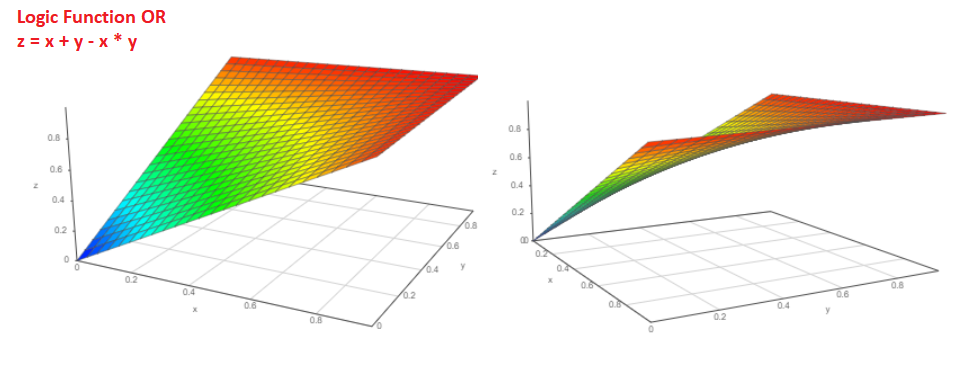
وإذا علمنا احتمالية وقوع الحدث Pa ، فما هو احتمال عدم وقوع الحدث؟
ع = 1 - باسكال.
الآن دعنا نفترض. تخيل أن لدينا عناصر منطقية تحسب احتمالية حدث الإخراج ، مع العلم باحتمالية أحداث الإدخال:
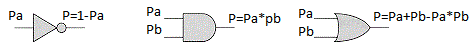
إن امتلاك هذه العناصر المنطقية يمكن أن يجعلها أكثر تعقيدًا ، على سبيل المثال ، حصريًا أو XOR:
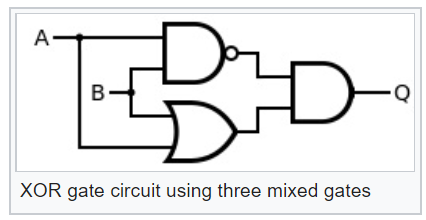
الآن ، بالنظر إلى الرسم التخطيطي لعنصر المنطق XOR هذا ، يمكننا أن نفهم ما هو احتمال الحدث عند إخراج الاحتمال XOR:
لكن هذا ليس كل شيء نحن نعلم المنطق النموذجي للمُعلِم الكامل ونكتشف كيف يُصنع المُعلِم متعدد البتات من مُعلِن كامل:
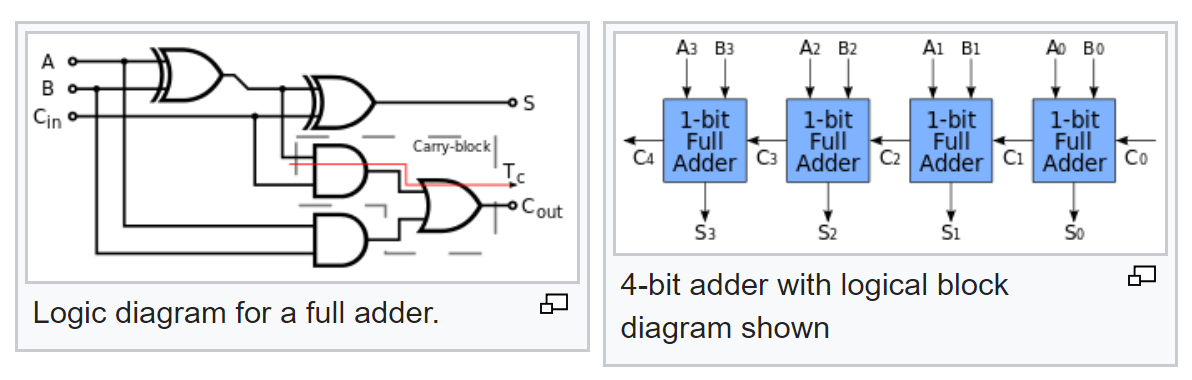
حتى الآن ، وفقًا لمخططه ، يمكننا الآن حساب احتمالات الإشارات عند خرجها ، مع الاحتمالات المعروفة للإشارات عند الإدخال.
وهكذا ، يمكنني تنفيذ فئة "32 بت" الخاصة بي (سأطلق عليها x32) مع الحساب الاحتمالي ، وتجاوز هذه الفئة لجميع عمليات sha256 مثل AND و OR و XOR و ADD والتحولات. سيخزن الفصل 32 بتة في الداخل ، لكن كل بت هو رقم فاصلة عائمة. ستحسب كل عملية منطقية أو حسابية على رقم 32 بت احتمالية قيمة كل بت بمعلمات إدخال معروفة أو غير معروفة لعملية منطقية أو حسابية.
فكر في مثال بسيط جدًا يستخدم الرياضيات الاحتمالية:
typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10); x32 a = 0xaabbccdd; x32 b = 0x12345678; <b>
في هذا المثال ، تتم إضافة رقمين 32 بت.
بينما السلسلة هي b.setBit (4، 0.75)؛ يتم التعليق على نتيجة الإضافة بشكل يمكن التنبؤ به وتحديده مسبقًا ، لأن جميع بيانات الإدخال للإضافة معروفة. يطبع البرنامج هذا على وحدة التحكم:
result = 0xbcf02355 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 1 bit5 = 0 bit6 = 1 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1
إذا ألغيت تعليق السطر b.setBit (4 ، 0.75) ، فعند القيام بذلك ، سأقول للبرنامج: "أضف هذين الرقمين إلي ، لكنني لا أعرف حقًا قيمة البتة 4 من الوسيطة الثانية ، أعتقد أنها واحدة مع احتمال 0.75".
ثم تحدث الإضافة ، كما ينبغي ، مع حساب كامل لاحتمالات إشارات الخرج ، أي البتات:
bit not stable bit not stable bit not stable result = 0xbcf02305 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 0.75 bit5 = 0.1875 bit6 = 0.8125 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1
نظرًا لحقيقة أن بيانات الإدخال لم تكن معروفة جدًا ، فإن النتيجة ليست معروفة جدًا. علاوة على ذلك ، ما يمكن حسابه بشكل موثوق يعتبر موثوقًا. ما لا يمكن احتسابه يعتبر محتملاً.
الآن بعد أن حصلت على فئة رائعة من 32 بت c ++ للحساب الضبابي ، يمكنني تمرير صفائف المتغيرات من نوع x32 إلى دالة full_btc_hash () في القالب والحصول على نتيجة تجزئة مقدرة محتملة.
بعض تطبيقات فئة x32 هي: #pragma once #include <string> #include <list> #include <iostream> #include <utility> #include <stdint.h> #include <vector> #include <limits> using namespace std; #include <boost/math/constants/constants.hpp> #include <boost/multiprecision/cpp_dec_float.hpp> using boost::multiprecision::cpp_dec_float_50; //typedef double MY_FP; typedef cpp_dec_float_50 MY_FP; class x32 { public: x32(); x32(uint32_t n); void init(MY_FP val); void init(double* pval); void setBit(int i, MY_FP val) { bvi[i] = val; }; ~x32() {}; x32 operator|(const x32& right); x32 operator&(const x32& right); x32 operator^(const x32& right); x32 operator+(const x32& right); x32& x32::operator+=(const x32& right); x32 operator~(); x32 operator<<(const unsigned int& right); x32 operator>>(const unsigned int& right); void print(); uint32_t get32(); MY_FP get_bvi(uint32_t idx) { return bvi[idx]; }; private: MY_FP not(MY_FP a); MY_FP and(MY_FP a, MY_FP b); MY_FP or (MY_FP a, MY_FP b); MY_FP xor(MY_FP a, MY_FP b); MY_FP bvi[32]; //bit values }; #include "stdafx.h" #include "x32.h" x32::x32() { for (int i = 0; i < 32; i++) { bvi[i] = 0.0; } } x32::x32(uint32_t n) { for (int i = 0; i < 32; i++) { bvi[i] = (n&(1 << i)) ? 1.0 : 0.0; } } void x32::init(MY_FP val) { for (int i = 0; i < 32; i++) { bvi[i] = val; } } void x32::init(double* pval) { for (int i = 0; i < 32; i++) { bvi[i] = pval[i]; } } x32 x32::operator<<(const unsigned int& right) { x32 t; for (int i = 31; i >= 0; i--) { if (i < right) { t.bvi[i] = 0.0; } else { t.bvi[i] = bvi[i - right]; } } return t; } x32 x32::operator>>(const unsigned int& right) { x32 t; for (unsigned int i = 0; i < 32; i++) { if (i >= (32 - right)) { t.bvi[i] = 0; } else { t.bvi[i] = bvi[i + right]; } } return t; } MY_FP x32::not(MY_FP a) { return 1.0 - a; } MY_FP x32::and(MY_FP a, MY_FP b) { return a * b; } MY_FP x32::or(MY_FP a, MY_FP b) { return a + b - a * b; } MY_FP x32::xor (MY_FP a, MY_FP b) { //(~(A & B)) & (A | B) return and( not( and(a,b) ) , or(a,b) ); } x32 x32::operator|(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = or ( bvi[i], right.bvi[i] ); } return t; } x32 x32::operator&(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = and (bvi[i], right.bvi[i]); } return t; } x32 x32::operator~() { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = not(bvi[i]); } return t; } x32 x32::operator^(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = xor (bvi[i], right.bvi[i]); } return t; } x32 x32::operator+(const x32& right) { x32 r; r.bvi[0] = xor (bvi[0], right.bvi[0]); MY_FP cout = and (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); r.bvi[i] = xor( xor_a_b, cout ); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); cout = or (and1,and2); } return r; } x32& x32::operator+=(const x32& right) { MY_FP cout = and (bvi[0], right.bvi[0]); bvi[0] = xor (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); bvi[i] = xor (xor_a_b, cout); cout = or (and1, and2); } return *this; } void x32::print() { for (int i = 0; i < 32; i++) { cout << bvi[i] << "\n"; } } uint32_t x32::get32() { uint32_t r = 0; for (int i = 0; i < 32; i++) { if (bvi[i] == 1.0) r = r | (1 << i); else if (bvi[i] == 0.0) { //ok } else { //oops.. cout << "bit not stable\n"; } } return r; }
ما كل هذا؟
لا يعرف منجم البيتكوين مقدمًا القيمة التي يجب تحديدها 32 ضعفًا. يضطر عامل المناجم إلى تكرار أكثر من 4 مليارات منهم من أجل حساب التجزئة حتى تصبح "جميلة" ، حتى تصبح قيمة التجزئة أقل من الهدف.
يتيح لك الحساب الاحتمالي الضبابي نظريًا التخلص من البحث الشامل.
نعم ، في البداية لا أعرف معنى كل البتات غير المطلوبة. إذا لم أكن أعرفهم ، فلا داعي للقلق - الاحتمال الأولي للبتات هو 0.5. حتى في هذا السيناريو ، يمكنني حساب احتمال بتات تجزئة الإخراج. في مكان ما يتحولون أيضًا إلى حوالي 0.5 زائد أو ناقص نصف بنس.
ومع ذلك ، يمكنني الآن تغيير بت واحد غير مرئي واحد فقط من 0.5 إلى 0.9 أو إلى 0.1 أو 1.0 ومعرفة كيف تتغير قيمة الاحتمال لقيمة الإشارة لكل بت من دالة التجزئة في الإخراج. لدي الآن المزيد من معلومات التقييم. يمكنني الآن أن أشعر بكل إدخال غير مرئي بشكل فردي ونرى أين يتغير احتمال الإشارة على كل من بتات الإخراج لدالة التجزئة.على سبيل المثال ، هنا جزء يأخذ في الاعتبار دالة التجزئة مع عدم البتات غير المعروفة تمامًا ، عندما يكون احتمال قيمة البت الخاصة به هو 0.5 والحساب الثاني ، عندما نفترض أن قيمة البت nonce [0] = 0.9: typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10);
تُرجع الدالة class x32 :: get_bvi () احتمالية قيمة البت لهذا الرقم.نحن نحسب ونرى أنه إذا قمت بتغيير قيمة البت nonce [0] من 0.5 إلى 0.9 ، فإن بعض البتات من الناتج بالكاد تتمايل ، وبعضها بالكاد يتمايل: 0.44525679540883948 0.44525679540840074 0.55268174813167364 0.5526817481315932 0.57758654725359399 0.57758654725360606 0.49595026978928474 0.49595026978930477 0.57118578561406703 0.57118578561407746 0.53237003739057907 0.5323700373905661 0.57269859374138096 0.57269859374138162 0.57631236396381141 0.5763123639638157 0.47943176373960149 0.47943176373960219 0.54955992675177704 0.5495599267517755 0.53321116270879686 0.53321116270879733 0.57294025883744952 0.57294025883744984 0.53131857821387693 0.53131857821387655 0.57253530821899101 0.57253530821899102 0.50661432403287194 0.50661432403287198 0.57149419848354913 0.57149419848354916 0.53220327148366491 0.53220327148366487 0.57268927270412251 0.57268927270412251 0.57632130426913003 0.57632130426913005 0.57233970084776142 0.57233970084776143 0.56824728628552812 0.56824728628552813 0.45247155441889921 0.45247155441889922 0.56875940568326509 0.56875940568326509 0.57524323439326321 0.57524323439326321 0.57587726902392535 0.57587726902392535 0.57597043124557292 0.57597043124557292 0.52847748894672118 0.52847748894672118 0.54512141953055808 0.54512141953055808 0.57362254577539695 0.57362254577539695 0.53082194129771177 0.53082194129771177 0.54404489702929382 0.54404489702929382 0.54065386336136847 0.54065386336136847
نوع من التنفس من النسيم ، وهو تغير ملحوظ بالكاد في احتمال الخروج في مكان عشري 10 م. حسنًا ، مع ذلك ... يمكنك محاولة بناء بعض الافتراضات حول ذلك. اتضح بشكل جميل ، أليس كذلك؟بالمناسبة ، إذا تمت تهيئة بتات الإدخال لغير المدخلات بقيم الاحتمالية الصحيحة والضرورية ، مثل هذا: double nonce_bits[32]; for (int i = 0; i < 32; i++) nonce_bits[i] = (real_nonce32&(1 << i)) ? 1.0 : 0.0; x32 nonce_x32; nonce_x32.init(nonce_bits); full_btc_hash(strxx, nonce_x32, result_x32);
ثم عند حساب التجزئة الاحتمالية نحصل على النتيجة المنطقية الصحيحة - تجزئة "جميلة" عند الإخراج ، البنغو.لذا مع الرياضيات ، كل شيء هنا.يبقى أن نتعلم كيف نحلل نسيم النسيم ... والتجزئة مكسورة.يبدو هذا هراء ، لكن هذا هراء - وحذرت في البداية.مواد مفيدة أخرى:- Minc Bitcoin بالورق والقلم.
- هل من الممكن حساب البيتكوين بشكل أسرع أم أسهل أم أسهل؟
- كيف فعلت عامل المناجم blakecoin
- FPGA عامل منجم بيتكوين على لوح مارس روفر 3
- FPGA Miner مع خوارزمية Blake