تطبيق FPGA Integer FFT

مرحبا بالجميع!

ذات مرة ، سألني العملاء عما إذا كان لدي عدد صحيح من FFT في مشاريعي ، والتي أجبت دائمًا على أن هذا قد تم بالفعل من قبل الآخرين في شكل نوى IP جاهزة ، وإن كانت منحنية ، ولكن مجانية (Altera / Xilinx) - خذها واستخدمها. ومع ذلك ، فإن هذه النوى ليست مثالية ، ولها مجموعة من "الميزات" وتتطلب المزيد من التحسين. في هذا الصدد ، بعد أن ذهبت في إجازة أخرى مخططة ، والتي لم أرغب في إنفاقها دون المتوسط ​​، بدأت في تنفيذ النواة القابلة للتكوين من FFT الصحيح.


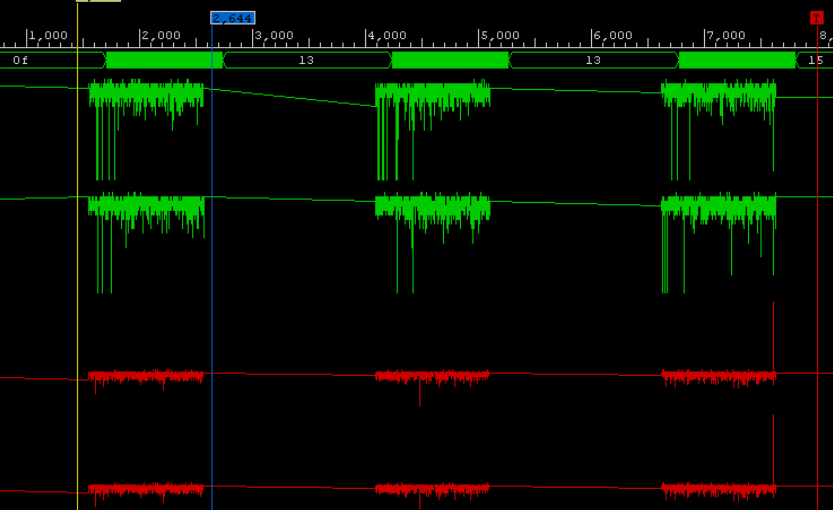_{KDPV (عملية تصحيح أخطاء تجاوز البيانات)}

في هذا المقال ، أريد أن أخبرك بالطرق والوسائل التي تتحقق من العمليات الحسابية عند حساب تحويل فورييه السريع بتنسيق صحيح على بلورات FPGA الحديثة. أساس أي FFT هو عقدة تسمى "الفراشة". تقوم الفراشة بتنفيذ العمليات الرياضية - الجمع والضرب والطرح. يتعلق الأمر بتطبيق "الفراشة" ونقاطها النهائية التي ستبدأ القصة أولاً. استنادًا إلى عائلات Xilinx FPGA الحديثة - تتأثر سلسلة Ultrascale و Ultrascale + ، بالإضافة إلى السلسلة القديمة 6- (Virtex) و 7- (Artix و Kintex و Virtex). لا تهتم السلسلة القديمة في المشاريع الحديثة في عام 2018. الغرض من المقالة هو الكشف عن ميزات تنفيذ نواة مخصصة لمعالجة الإشارات الرقمية باستخدام مثال FFT.

مقدمة

لا يخفى على أحد أن خوارزميات أخذ FFT متجذرة بقوة في حياة مهندسي معالجة الإشارات الرقمية ، وبالتالي فهذه الأداة مطلوبة باستمرار. لدى الشركات المصنعة الرائدة في FPGA مثل Altera / Xilinx بالفعل نوى FFT / IFFT قابلة للتشكيل ، ولكن لديهم عدد من القيود والميزات ، وبالتالي اضطررت إلى استخدام تجربتي الخاصة أكثر من مرة. لذا هذه المرة كان علي تنفيذ FFT بتنسيق صحيح وفقًا لمخطط Radix-2 على FPGA. في مقالتي الأخيرة ، قمت بالفعل بعمل FFT في تنسيق النقطة العائمة ، ومن هناك تعرف أن الخوارزمية ذات التوازي المزدوج تستخدم لتنفيذ FFT ، أي أن النواة يمكنها معالجة عينتين معقدتين بنفس التردد . هذه إحدى ميزات FFT الرئيسية غير المتوفرة في حبات Xilinx FFT الجاهزة.

مثال: يلزم تطوير عقدة FFT تؤدي التشغيل المستمر لتيار الإدخال للأعداد المركبة بتردد 800 ميجاهرتز. لن يقوم قلب Xilinx بسحب هذا (ترددات ساعة المعالجة القابلة للتحقيق في FPGAs الحديثة بترتيب 300-400 ميجاهرتز) ، أو سيتطلب تدمير تيار الإدخال بطريقة أو بأخرى. يسمح لك النواة المخصصة بتسجيل ساعتين من المدخلات بتردد 400 ميجاهرتز دون تدخل مسبق ، بدلاً من عينة واحدة عند 800 ميجاهرتز. ناقص آخر من Xilinx FFT هو عدم القدرة على قبول تدفق الإدخال بترتيب عكسي . في هذا الصدد ، يتم إنفاق موارد ذاكرة شريحة FPGA ضخمة لإعادة ترتيب البيانات بترتيب عادي. بالنسبة لمهام الالتواء السريع للإشارات ، عندما تقف عقدتان FFT خلف بعضهما البعض ، يمكن أن تصبح هذه لحظة حرجة ، أي أن المهمة لن تكمن في شريحة FPGA المحددة. يسمح لك قلب FFT المخصص بتلقي البيانات بالترتيب العادي عند الإدخال ، وإخراجها في وضع عكسي للبت ، في حين أن قلب FFT المعكوس - على العكس من ذلك ، يتلقى البيانات بترتيب عكسي للبت ، ويخرجها في الوضع العادي. يتم تخزين اثنين من المخازن المؤقتة لتبديل البيانات في وقت واحد !!!

نظرًا لأن معظم المواد في هذه المقالة يمكن أن تتداخل مع المادة السابقة ، فقد قررت التركيز على موضوع العمليات الرياضية بتنسيق صحيح على FPGA لتنفيذ FFT.

معلمات نواة FFT

• NFFT - عدد الفراشات (طول FFT) ،
• DATA_WIDTH - عمق البت لبيانات الإدخال (4-32) ،
• TWDL_WIDTH - عمق البت لعوامل الدوران (8-27).
• SERIES - يحدد عائلة FPGA التي يتم تنفيذ FFT عليها ("جديد" - Ultrascale ، "OLD" - 6/7 Xilinx FPGA series).

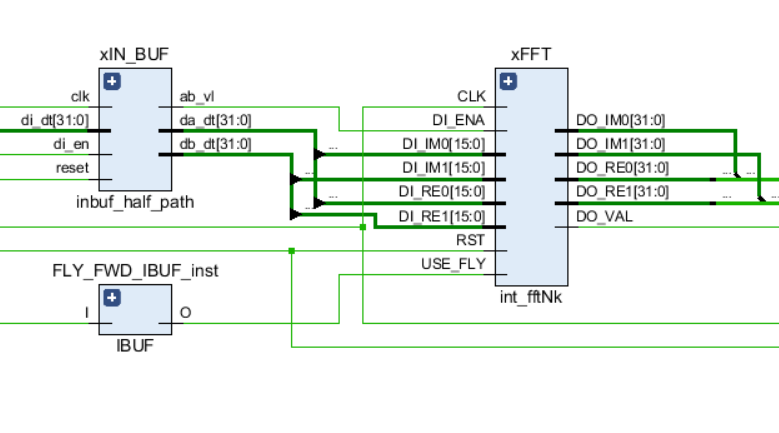
مثل أي روابط أخرى في الدائرة ، يحتوي FFT على منافذ للتحكم في الإدخال - إشارة على مدار الساعة وإعادة ضبط ، بالإضافة إلى منافذ بيانات الإدخال والإخراج. بالإضافة إلى ذلك ، يتم استخدام إشارة USE_FLY في النواة ، مما يسمح لك بإيقاف تشغيل فراشات FFT ديناميكيًا من أجل عمليات التصحيح أو مشاهدة دفق الإدخال الأصلي.

يوضح الجدول أدناه مقدار موارد FPGA المستخدمة ، اعتمادًا على طول NFFT FFT لـ DATA_WIDTH = 16 وقطعتين TWDL_WIDTH = 16 و 24 بت.



المركز عند NFFT = 64K مستقر عند تردد المعالجة FREQ = 375 ميجاهرتز على بلورة Kintex-7 (410T).

هيكل المشروع

يظهر الرسم التخطيطي للعقدة FFT في الشكل التالي:


لتسهيل فهم ميزات بعض المكونات ، سأقدم قائمة بملفات المشروع ووصفها المختصر بترتيب هرمي:

• نواة FFT:
  
  • int_fftNk - عقدة FFT ، دائرة Radix-2 ، هدم التردد (DIF) ، دفق الإدخال طبيعي ، دفق الإخراج عكسي.
  • int_ifftNk - عقدة OBPF ، دائرة Radix-2 ، هلاك الوقت (DIT) ، دفق الإدخال معكوس قليلاً ، دفق الإخراج طبيعي.
• الفراشات:
  
  
  • int_dif2_fly - فراشة Radix-2 ، اضمحلال التردد ،
  • int_dit2_fly - فراشة Radix-2 ، الهلاك في الوقت المناسب ،
• مضاعفات معقدة:
  
  
  • int_cmult_dsp48 - مضاعف شكلي عام يشمل:
  • int_cmult18x25_dsp48 - مضاعف الأعماق الصغيرة للبيانات وعوامل الدوران ،
  • int_cmult_dbl18_dsp48 - مضاعف مضاعف ، عرض البت لعوامل الدوران حتى 18 بت ،
  • int_cmult_dbl35_dsp48 - مضاعف مضاعف ، عرض البت لعوامل الدوران حتى 25 * بت ،
  • int_cmult_trpl18_dsp48 - مضاعف ثلاثي ، سعة عوامل الدوران حتى 18 بت ،
  • int_cmult_trpl52_dsp48 - مضاعف ثلاثي ، سعة العوامل الدورية حتى 25 * بت ،
• المضاعفات:
  
  
  • mlt42x18_dsp48e1 - مضاعف بتات المعاملات حتى 42 و 18 بت على أساس DSP48E1 ،
  • mlt59x18_dsp48e1 - مضاعف بتات المعامل حتى 59 و 18 بت بناءً على DSP48E1 ،
  • mlt35x25_dsp48e1 - مضاعف بتات المعاملات حتى 35 و 25 بت على أساس DSP48E1 ،
  • mlt52x25_dsp48e1 - مضاعف بتات المعاملات حتى 52 و 25 بت على أساس DSP48E1 ،
  • mlt44x18_dsp48e2 - مضاعف بت معاملات تصل إلى 44 و 18 بت على أساس DSP48E2 ،
  • mlt61x18_dsp48e2 - مضاعف بتات المعامل حتى 61 و 18 بت بناءً على DSP48E2 ،
  • mlt35x27_dsp48e2 - مضاعف بتات المعامل حتى 35 و 27 بت بناءً على DSP48E2 ،
  • mlt52x27_dsp48e2 هو مضاعف بتات المعامل حتى 52 و 27 بت على أساس DSP48E2.
• المجمع:
  
  
  • int_addsub_dsp48 - مُجمع عالمي ، بت المعامل حتى 96 بت.
• خطوط التأخير:
  
  
  • int_delay_line - خط الأساس للتأخير ، يوفر تبديل البيانات بين الفراشات ،
  • int_align_fft - محاذاة بيانات الإدخال وعوامل التحول عند إدخال فراشة FFT ،
  • int_align_fft - محاذاة بيانات الإدخال وعوامل التحول عند إدخال فراشة OBPF ،
• العوامل الدورية:
  
  
  • rom_twiddle_int - مولد للعوامل الدوارة ، من طول معين ، يعتبر FFT المعاملات على أساس خلايا DSP FPGA ،
  • row_twiddle_tay - مولد العوامل الدوارة باستخدام سلسلة Taylor (NFFT> 2K) **.
• مخزن البيانات المؤقت:
  
  
  • inbuf_half_path - مخزن الإدخال المؤقت ، يستقبل الدفق في الوضع العادي وينتج تسلسلين من العينات المحولة بمقدار نصف طول FFT *** ،
  • outbuf_half_path - المخزن المؤقت للإخراج ، يجمع تسلسلين وينتج واحدًا مستمرًا يساوي طول FFT ،
  • iobuf_flow_int2 - يعمل المخزن المؤقت في وضعين: يتلقى دفقًا في وضع Interleave-2 وينتج تسلسلين من FFT يتم إزالتهما بنصف الطول. أو العكس ، اعتمادًا على خيار BITREV.
  • int_bitrev_ord هو محول بيانات بسيط من الترتيب الطبيعي إلى عكس البت.

* - لـ DSP48E1: 25 بت ، لـ DSP48E2 - 27 بت.
** - من مرحلة معينة من FFT ، يمكن استخدام كمية ثابتة من ذاكرة الكتلة لتخزين معاملات الدوران ، ويمكن حساب المعاملات المتوسطة باستخدام عقد DSP48 باستخدام صيغة تايلور إلى المشتق الأول. نظرًا لحقيقة أن مورد الذاكرة أكثر أهمية بالنسبة إلى FFT ، يمكنك التضحية بأمان بوحدات الحوسبة من أجل الذاكرة.
*** - المخزن المؤقت للإدخال وخطوط التأخير - تقديم مساهمة كبيرة في مقدار موارد ذاكرة FPGA المشغولة

الفراشة

يعلم كل شخص واجه مرة واحدة على الأقل خوارزمية تحويل فورييه السريعة أن هذه الخوارزمية تستند إلى عملية أولية - "الفراشة". يحول تيار الإدخال بضرب الإدخال في عامل اللف. هناك نوعان من مخططات التحويل الكلاسيكية ل FFTs - الهلاك في التردد (DIF ، التدمير في التردد) والهلاك في الوقت (DIT ، التدمير في الوقت). تتميز خوارزمية DIT بتقسيم تسلسل الإدخال إلى تسلسلين بنصف المدة ، وخوارزمية DIF إلى سلسلتين من العينات الزوجية والفردة لمدة NFFT. بالإضافة إلى ذلك ، تختلف هذه الخوارزميات في العمليات الرياضية لعملية الفراشة.



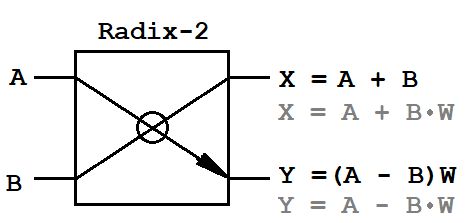أ ، ب - أزواج الإدخال من العينات المعقدة ،
X ، Y - أزواج إخراج عينات معقدة ،
ث - عوامل تحول معقدة.

نظرًا لأن بيانات الإدخال هي كميات معقدة ، فإن الفراشة تتطلب مضاعفًا معقدًا واحدًا (4 عمليات الضرب و 2 عمليات الجمع) واثنين من المضافات المعقدة (4 عمليات الجمع). هذا هو الأساس الرياضي الكامل الذي يجب تنفيذه على FPGA.

المضاعف

وتجدر الإشارة إلى أن جميع العمليات الحسابية على FPGAs غالبًا ما يتم إجراؤها في كود إضافي (مكمل 2). يمكن تنفيذ مضاعف FPGA بطريقتين - على المنطق باستخدام مشغلات وجداول LUT ، أو على وحدات حساب DSP48 الخاصة ، والتي تم تضمينها بثبات وطويلة في جميع FPGA الحديثة. في الكتل المنطقية ، يتم تنفيذ الضرب باستخدام خوارزمية Booth أو تعديلاتها ، ويأخذ كمية مناسبة من الموارد المنطقية ولا يفي دائمًا بقيود الوقت عند ترددات معالجة البيانات العالية. في هذا الصدد ، يتم دائمًا تصميم مضاعفات FPGA في المشاريع الحديثة على أساس عقد DSP48 وأحيانًا فقط على المنطق. العقدة DSP48 هي خلية منتهية معقدة تنفذ وظائف رياضية ومنطقية. العمليات الأساسية: الضرب ، الجمع ، الطرح ، التراكم ، العداد ، العمليات المنطقية (XOR ، NAND ، AND ، OR ، NOR) ، التربيع ، مقارنة الأرقام ، التحول ، إلخ. يوضح الشكل التالي خلية DSP48E2 لعائلة Xilinx Ultrascale + FPGA.



من خلال تكوين بسيط لمنافذ الإدخال ، وعمليات الحساب في العُقد وتعيين التأخيرات داخل العقدة ، يمكنك عمل درس رياضي عالي السرعة للبيانات الرياضية.
لاحظ أن جميع كبار موردي FPGA في بيئة التطوير لديهم نوى IP قياسية ومجانية لحساب الوظائف الرياضية بناءً على عقدة DSP48. إنها تسمح لك بحساب الوظائف الرياضية البدائية وتعيين تأخيرات مختلفة عند إدخال وإخراج العقدة. بالنسبة لـ Xilinx ، هذا هو "مضاعف" IP-Core (الإصدار 12.0 ، 2018) ، والذي يسمح لك بتكوين المضاعف لأي عمق بت لبيانات الإدخال من 2 إلى 64 بت. بالإضافة إلى ذلك ، يمكنك تحديد كيفية تنفيذ المضاعف - على الموارد المنطقية أو على بدائية DSP48 المضمنة.

تقدير مقدار منطق "يأكل" المضاعف مع عمق البت لبيانات الإدخال على المنفذين A و B = 64 بت. إذا كنت تستخدم العقد DSP48 ، فستحتاج إلى 16 فقط.



القيد الرئيسي على خلايا DSP48 هو عمق البت لبيانات الإدخال. العقدة DSP48E1 ، وهي الخلية الأساسية لسلسلة FPGA Xilinx 6 و 7 ، عرض منافذ الإدخال للضرب: "A" - 25 بت ، "B" - 18 بت ، وبالتالي ، فإن نتيجة الضرب هي رقم 43 بت. بالنسبة لعائلة Xilinx Ultrascale و Ultrascale + FPGA ، خضعت العقدة لعدة تغييرات ، على وجه الخصوص ، زادت سعة المنفذ الأول بمقدار بتتين: "أ" - 27 بت ، "ب" - 18 - بت. بالإضافة إلى ذلك ، تسمى العقدة نفسها DSP48E2.

لكي لا تكون مرتبطة بأسرة معينة وشريحة FPGA ، لضمان "نقاء كود المصدر" ، ولمراعاة جميع أعماق البتات المحتملة لبيانات الإدخال ، تقرر تصميم مجموعة المضاعفات الخاصة بنا. سيسمح هذا بالتنفيذ الأكثر فعالية للمضاعفات المعقدة لفراشات FFT ، أي المضاعفات وطرح - المستخلص بناءً على كتل DSP48. المدخل الأول للمضاعف هو بيانات الإدخال ، والمدخل الثاني للمضاعف هو العوامل الدورية (الإشارة التوافقية من الذاكرة). يتم تنفيذ مجموعة من المضاعفات باستخدام مكتبة UNISIM المدمجة ، والتي من الضروري توصيل DSP48E1 و DSP48E2 البدائيين لاستخدامها في المشروع. يتم عرض مجموعة من المضاعفات في الجدول. وتجدر الإشارة إلى أن:

• يؤدي تشغيل الأعداد المضاعفة إلى زيادة سعة المنتج كمجموع سعة المعاملات.
• كل من المضاعفات 25x18 و 27x18 مكررة ، في الواقع - هذا مكون واحد للعائلات المختلفة.
• كلما زادت مرحلة التوازي للعملية ، زاد التأخير في الحوسبة وزاد حجم الموارد المشغولة.
• مع عمق بت أقل عند الإدخال "B" ، يمكن تنفيذ مضاعفات بعمق بت أعلى عند إدخال آخر.
• يتم تقديم القيد الرئيسي لزيادة عمق البت بواسطة المنفذ "B" (المنفذ الحقيقي لـ DSP48 البدائي) وتسجيل التحول الداخلي بمقدار 17 بت.

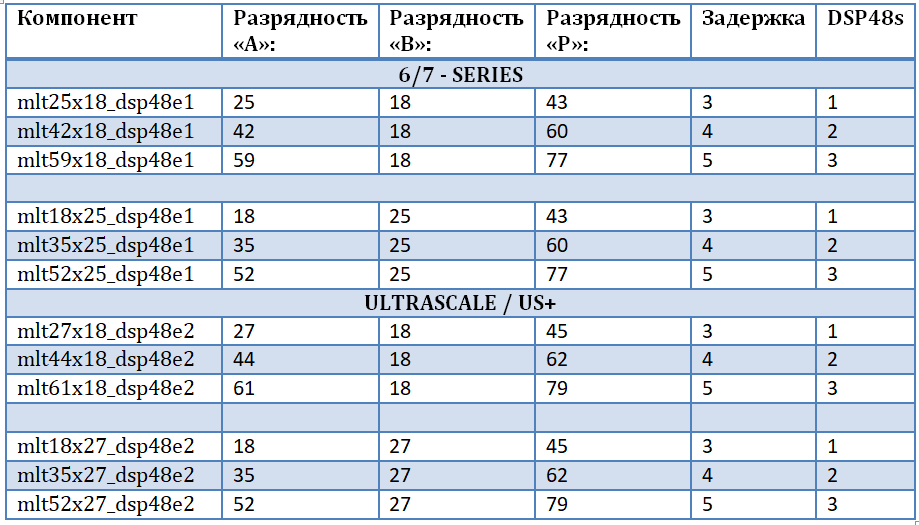
زيادة الاهتمام بعمق البتات ليست ذات أهمية في إطار المهمة للأسباب الموضحة أدناه:

عمق بت عوامل التحول

من المعروف أنه كلما زادت دقة الإشارة التوافقية ، كلما كان الرقم أكثر دقة (كلما زادت العلامات في الجزء الكسري). لكن حجم بت المنفذ هو B <25 بت بسبب حقيقة أن عمق البت يكفي لعوامل الدوران في عقد FFT ، لضمان الضرب عالي الجودة لتدفق الإدخال مع عناصر الإشارة التوافقية في "الفراشات" (لأي أطوال قابلة للتحقيق واقعيًا على FPGAs). القيمة النموذجية لعمق البت لمعاملات الدوران في المهام التي أقوم بتنفيذها هي 16 بت ، 24 - أقل في كثير من الأحيان ، 32 - أبدًا.

عمق بت عينات المدخلات

سعة هذه العقد النموذجية للاستقبال والتسجيل (ADCs ، DACs) ليست كبيرة - من 8 إلى 16 بت ، ونادرًا - 24 أو 32 بت. علاوة على ذلك ، في الحالة الأخيرة ، يكون من الأفضل استخدام تنسيق بيانات النقطة العائمة وفقًا لمعيار IEEE-754. من ناحية أخرى ، تضيف كل مرحلة من مراحل "الفراشة" في FFT قليلا من البيانات إلى عينات المخرجات بسبب العمليات الحسابية. على سبيل المثال ، لطول NFFT = 1024 ، يتم استخدام log2 (NFFT) = 10 فراشات.

لذلك ، سيكون عمق بت الإخراج أكبر 10 بت من الإدخال ، WOUT = WIN + 10. بشكل عام ، تبدو الصيغة كما يلي:

WOUT = WIN + log2 (NFFT) ؛

مثال:

عمق البت لتدفق الإدخال WIN = 32 بت ،
عمق البت لعوامل الدوران TWD = 27 ،
لا تتجاوز سعة المنفذ "A" من قائمة المضاعفات المنفذة في هذه المقالة 52 بت. هذا يعني أن الحد الأقصى لعدد الفراشات هو FFT = 52-32 = 20. أي أنه من الممكن تحقيق FFT بطول يصل إلى 2 ^ 20 = 1M عينات. (ومع ذلك ، من الناحية العملية ، هذا غير ممكن بالوسائل المباشرة بسبب محدودية الموارد حتى لأقوى بلورات FPGA ، ولكن هذا يتعلق بموضوع آخر ولن يتم تناوله في المقالة).

كما ترون ، هذا أحد الأسباب الرئيسية لعدم تنفيذ المضاعفات بعمق بت أعلى لمنافذ الإدخال. تغطي المضاعفات المستخدمة النطاق الكامل لأحجام بت المدخلات المطلوبة وعوامل الدوران لمهمة حساب العدد الصحيح من FFT. في جميع الحالات الأخرى ، يمكنك استخدام حساب FFT بتنسيق الفاصلة العائمة !

تنفيذ المضاعف "الواسع"

استنادًا إلى مثال بسيط لضرب رقمين لا يتناسبان مع عمق البت لعقدة DSP48 القياسية ، سأوضح كيف يمكنك تنفيذ مضاعف بيانات واسع. يوضح الشكل التالي مخطط كتلته. يضاعف المضاعف ضرب رقمين موقَّعين في الكود الإضافي ، عرض المعامل الأول X هو 42 بت ، والثاني Y هو 18 بت. يحتوي على عقدتين DSP48E2. يتم استخدام سجلين لموازنة التأخيرات في العقدة العليا. يتم ذلك لأنه في الأفعى العلوي تحتاج إلى إضافة الأرقام بشكل صحيح من العقد العلوية والسفلية من DSP48. لا يتم استخدام الأدمى السفلي بالفعل. عند إخراج العقدة السفلية ، هناك تأخير إضافي للمنتج لمحاذاة رقم الإخراج مع الوقت. التأخير الكلي هو 4 دورات.



يتكون العمل من مكونين:

• الجزء الأصغر: P1 = '0' & X [16: 0] * Y [17: 0] ؛
• الجزء الأقدم: P2 = X [42:17] * Y [17: 0] + (P1 >> 17) ؛

جهاز العد

مثل المضاعف ، يمكن بناء المُصمم على الموارد المنطقية باستخدام سلسلة نقل ، أو على كتل DSP48. لتحقيق أقصى إنتاجية ، يفضل الطريقة الثانية. يسمح بدائي DSP48 واحد بتنفيذ عملية الإضافة حتى 48 بت ، وعقدين حتى 96 بت. بالنسبة للمهمة الحالية ، فإن أعماق البت هذه كافية تمامًا. بالإضافة إلى ذلك ، يحتوي جهاز DSP48 البدائي على وضع "SIMD MODE" خاص ، والذي يوازي وحدة ALU المضمنة 48 بت في عدة عمليات مع بيانات مختلفة ذات سعة صغيرة. أي أنه في الوضع "ONE" يتم استخدام شبكة بت كاملة من 48 بت ومعاملين ، وفي الوضع "TWO" تنقسم شبكة البت إلى عدة تيارات متوازية لكل منها 24 بت (4 معاملات). يساعد هذا الوضع ، باستخدام مُعلِق واحد فقط ، على تقليل كمية موارد رقاقة FPGA المشغولة عند أعماق بت صغيرة لعينات الإدخال (في المراحل الأولى من الحساب).

زيادة عمق البت

تؤدي عملية ضرب رقمين مع البتتين N و M في رمز إضافي ثنائي إلى زيادة في سعة بت الإخراج إلى P = N + M.

مثال: لمضاعفة الأرقام المكونة من ثلاثة بتات N = M = 3 ، يكون الحد الأقصى للرقم الموجب +3 = (011) ₂ ، والحد الأقصى للرقم السالب هو 4 = (100) ₂ . البتة الأكثر أهمية هي المسؤولة عن علامة الرقم. لذلك ، فإن أقصى عدد ممكن عند الضرب هو +16 = (010000) ₂ ، والذي يتكون نتيجة لضرب رقمين سلبيين كحد أقصى -4. إن عمق البت للناتج يساوي مجموع بتات الإدخال P = N + M = 6 بتات.

تؤدي عملية إضافة رقمين مع البتتين N و M في الشفرة الإضافية الثنائية إلى زيادة بتات الإخراج بتة واحدة.

مثال: أضف رقمين موجبين ، N = M = 3 ، والحد الأقصى للرقم الموجب هو 3 = (011) ₂ ، والحد الأقصى للرقم السالب هو 4 = (100) ₂ . . , – 6 = (0110) ₂ , – -8 = (1000) ₂ . .

:
. . , 16- -32768 = 0x8000, -32767 = 0x8001. ~0.003% .

, . : – 4 = (100) ₂ , +3 = (011) ₂ . = -12 = (110100) ₂ . , .. , — .

:

, «» , , . M- , , . 0x8000 = -1, 0x7FFF = +1. , ( M ). , , 1 . , [N+M-1-1: M-1]. ( 1), – .

/ «» .

, FFT DIT FFT DIF W0 = {Re, Im} = {1, 0}. , – , . : «» . : W0 = {Re, Im} = {1, 0} W1 = {Re, Im} = {0, -1}. , . DSP48 .

– -, , .

- , . . — — .

INT_FFTK

• .
• NFFT = 8-512K .
• NFFT.
• , .
• , .
• .
• !
• .
• : – , -.
• : - , – .
• . Radix-2.
• NFFT *.
• .
• (Virtex-6, 7-Series, Ultrascale).
• ~375MHz Kintex-7
• – VHDL.
• bitreverse +.
• Open Source IP-Cores.

INTFFTK VHDL ( ) m- Matlab / Octave .

الخلاصة

, . , . , IP-CORE Xilinx. .

: Radix-4, Radix-8, Ultra-Long FFT , FFT-FP32 ( IEEE-754). , , . FFT Radix-8, ( ).

dsmv2014 , . شكرا لكم على اهتمامكم!

UPDATE 2018/08/22

SCALED FFT / IFFT . 1 (truncate LSB). = .

, , : . , - .

: — 6 . — 128 . NFFT = 1024 , DATA_WIDTH = 16, TWDL_WIDTH = 16.

, SCALED « » , UNSCALED .