نظرة عامة على خوارزمية مقابلة الوظيفة - تعيين الجيل

مرحبا يا هبر!

يبدأ هذا المنشور تحليل المهام وفقًا للخوارزميات التي تحبها شركات تكنولوجيا المعلومات الكبيرة (Mail.Ru Group و Google وما إلى ذلك) لإعطاء المرشحين للمقابلات (إذا كانت المقابلة مع الخوارزميات ليست جيدة ، فإن فرص الحصول على وظيفة في شركة الأحلام ، للأسف تميل إلى الصفر). بادئ ذي بدء ، هذا المنشور مفيد لأولئك الذين ليس لديهم خبرة في البرمجة الأولمبية أو الدورات الثقيلة مثل ShAD أو LKS ، حيث يتم أخذ مواضيع الخوارزميات بجدية كافية ، أو لأولئك الذين يرغبون في تحديث معرفتهم في مجال معين.

في الوقت نفسه ، لا يمكن القول بأن جميع المهام التي سيتم التعامل معها هنا سيتم بالتأكيد الوفاء بها في المقابلة ، ومع ذلك ، فإن الأساليب التي يتم بها حل هذه المهام متشابهة في معظم الحالات.

سيتم تقسيم السرد إلى مواضيع مختلفة ، وسنبدأ بتكوين مجموعات ذات بنية محددة.

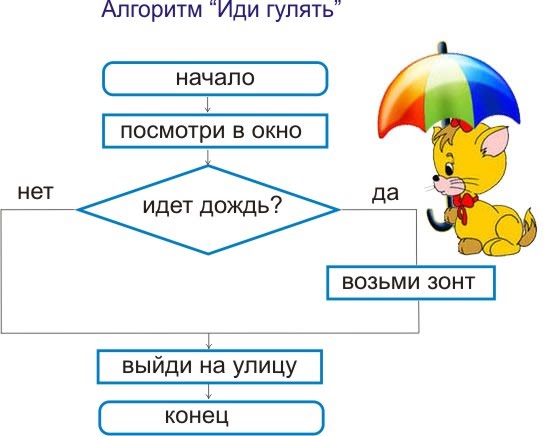
1. لنبدأ مع الأكورديون الزر: أنت بحاجة إلى إنشاء جميع تسلسلات الأقواس الصحيحة مع أقواس من نفس النوع ( ما هو تسلسل الأقواس الصحيح ) ، حيث يكون عدد الأقواس k.

يمكن حل هذه المشكلة بعدة طرق. لنبدأ بتكرار .

تفترض هذه الطريقة أننا بدأنا في التكرار عبر تسلسلات من قائمة فارغة. بعد إضافة القوس (الفتح أو الإغلاق) إلى القائمة ، يتم تنفيذ استدعاء العودية مرة أخرى ويتم فحص الشروط. ما هي الشروط؟ من الضروري مراقبة الفرق بين قوسي الفتح cnt (متغير cnt ) - لا يمكنك إضافة قوس إغلاق إلى القائمة إذا كان هذا الاختلاف غير إيجابي ، وإلا سيتوقف تسلسل القوس عن كونه صحيحًا. يبقى لتنفيذ هذا بعناية في التعليمات البرمجية.

 k = 6 #   init = list(np.zeros(k)) #  ,    cnt = 0 #    ind = 0 # ,       def f(cnt, ind, k, init): #  . ,     if (cnt <= k-ind-2): init[ind] = '(' f(cnt+1, ind+1, k, init) # .    ,  cnt > 0 if cnt > 0: init[ind] = ')' f(cnt-1, ind+1, k, init) #      if ind == k: if cnt == 0: print (init) 

تعقيد هذه الخوارزمية هو $$$O ((C_k ^ {k / 2} - C_k ^ {k / 2 -1}) * k)$مطلوب ذاكرة إضافية $$$O (k)$.

مع المعلمات المعينة ، استدعاء دالة $$$f (cnt، ind، k، init)$سيخرج ما يلي:

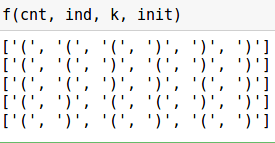
طريقة تكرارية لحل هذه المشكلة: في هذه الحالة ، ستكون الفكرة مختلفة بشكل أساسي - تحتاج إلى تقديم مفهوم الترتيب المعجمي لتسلسل الأقواس.

يمكن ترتيب جميع تسلسل الأقواس الصحيحة لنوع واحد من الأقواس مع مراعاة حقيقة ذلك $$$'(' <')'$. على سبيل المثال ، بالنسبة إلى n = 6 ، فإن التسلسل الأدنى المعجمية هو $$$((()))$والأقدم - $$$() () ()$.

للحصول على تسلسل المعاجم التالي ، تحتاج إلى العثور على قوس الفتح الموجود في أقصى اليمين ، والذي يوجد قبله قوس إغلاق ، بحيث عندما يكونون متبادلين ، يبقى تسلسل القوس صحيحًا. نقوم بتبديلها وجعل اللاحقة هي الأكثر استخدامًا في المعجم - لهذا تحتاج إلى حساب الفرق في كل خطوة بين عدد الأقواس.

في رأيي ، هذا النهج هو كئيب قليلاً من العودية ، ولكن يمكن استخدامه لحل المشاكل الأخرى لمجموعات التوليد. نقوم بتنفيذ هذا في التعليمات البرمجية.

 #  ,    n = 6 arr = ['(' for _ in range(n//2)] + [')' for _ in range(n//2)] def f(n, arr): #    print (arr) while True: ind = n-1 cnt = 0 #  . ,    while ind>=0: if arr[ind] == ')': cnt -= 1 if arr[ind] == '(': cnt += 1 if cnt < 0 and arr[ind] =='(': break ind -= 1 #   ,     if ind < 0: break #   .  arr[ind] = ')' #      for i in range(ind+1,n): if i <= (n-ind+cnt)/2 +ind: arr[i] = '(' else: arr[i] = ')' print (arr) 

تعقيد هذه الخوارزمية هو نفسه كما في المثال السابق.

بالمناسبة ، هناك طريقة بسيطة توضح أن عدد تتابعات الأقواس المولدة لنوع معين يجب أن يتطابق مع الأرقام الكاتالونية .

يعمل!

رائع ، مع وجود الأقواس في الوقت الحالي ، دعنا ننتقل إلى إنشاء مجموعات فرعية. لنبدأ بلغز بسيط.

2. إعطاء مصفوفة ترتيب تصاعدي بأرقام من $$$0$من قبل $$$n-1$، يلزم إنشاء كافة مجموعاته الفرعية.

لاحظ أن عدد المجموعات الفرعية لهذه المجموعة هو بالضبط $$$2 ^ n$. إذا تم تمثيل كل مجموعة فرعية كمجموعة من المؤشرات ، أين $$$0$يعني أن العنصر غير مدرج في المجموعة ، ولكن $$$1$- ما هو مدرج ، فإن توليد كل هذه المصفوفات سيكون جيل جميع المجموعات الفرعية.

إذا أخذنا بعين الاعتبار تمثيل البتات للأرقام من 0 إلى $$$2 ^ n - 1$، ثم سيحددون المجموعات الفرعية المطلوبة. أي لحل المشكلة ، من الضروري تنفيذ إضافة الوحدة إلى رقم ثنائي. نبدأ بكل الأصفار وننتهي بمصفوفة بها وحدات واحدة.

 n = 3 B = np.zeros(n+1) #  B   1  (    ) a = np.array(list(range(n))) #   def f(B, n, a): #   while B[0] == 0: ind = n #     while B[ind] == 1: ind -= 1 #   1 B[ind] = 1 #      B[(ind+1):] = 0 print (a[B[1:].astype('bool')]) 

تعقيد هذه الخوارزمية هو $$$O (n * 2 ^ n)$من الذاكرة - $$$O (n)$.

الآن دعونا نعقد المهمة السابقة قليلاً.

3. إعطاء مجموعة مرتبة بترتيب تصاعدي بأرقام من $$$0$من قبل $$$n-1$، تحتاج إلى إنشاء كل ذلك $$$k$- مجموعات فرعية للعناصر (يتم حلها بشكل متكرر).

ألاحظ أن صياغة هذه المشكلة تشبه المشكلة السابقة ويمكن حلها باستخدام نفس المنهجية تقريبًا: خذ المصفوفة الأولية مع $$$k$الوحدات و $$$n-k$الأصفار والفرز بالتسلسل من خلال جميع المتغيرات من هذه التسلسلات من الطول $$$n.$

ومع ذلك ، هناك حاجة إلى تغييرات طفيفة. نحن بحاجة إلى فرز كل شيء $$$k$مجموعات من القيم بقيمة من $$$0$من قبل $$$n-1$. عليك أن تفهم بالضبط كيف تحتاج إلى الفرز عبر المجموعات الفرعية. في هذه الحالة ، يمكننا تقديم مفهوم الترتيب المعجمي لمثل هذه المجموعات.

نرتب أيضًا التسلسل حسب رموز الأحرف: $$$1 <0$(هذا ، بالطبع ، غريب ، لكنه ضروري ، والآن سنفهم السبب). على سبيل المثال $$$n = 4، k = 2$الأصغر والأكبر سيكون التسلسل $$$[1،1،0،0]$و $$$[0،0،1،1]$.

يبقى أن نفهم كيفية وصف الانتقال من تسلسل إلى آخر. كل شيء بسيط هنا: إذا تغيرنا $$$1$على $$$0$، ثم على اليسار نكتب الحد الأدنى المعجمية مع مراعاة الحفاظ على الشرط $$$k$. الكود:

 n = 5 k = 3 a = np.array(list(range(n))) #    k -   init = [1 for _ in range(k)] + [0 for _ in range(nk)] def f(a, n, k, init): #   k-  print (a[a[init].astype('bool')]) while True: unit_cnt = 0 cur_ind = 0 #   ,     1 while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0): if init[cur_ind] == 1: unit_cnt += 1 cur_ind += 1 #        -    if cur_ind == n: break #  init[cur_ind] = 1 #   . .  for i in range(cur_ind): if i < unit_cnt-1: init[i] = 1 else: init[i] = 0 print (a[a[init].astype('bool')]) 

مثال العمل:

تعقيد هذه الخوارزمية هو $$$O (C_n ^ k * n)$من الذاكرة - $$$O (n)$.

4. إعطاء مجموعة ترتيب تصاعدي بأرقام من $$$0$من قبل $$$n-1$، تحتاج إلى إنشاء كل ذلك $$$k$- عناصر فرعية (حل بشكل متكرر).

الآن دعونا نحاول العودية. الفكرة بسيطة: هذه المرة بدون وصف ، انظر الكود.

 n = 5 a = np.array(list(range(n))) ind = 0 # ,       num = 0 # ,       k = 3 sub = list(-np.ones(k)) #  def f(n, a, num, ind, k, sub): #   k  ,     if ind == k: print (sub) else: for i in range(n - num): #  ,      k  if (n - num - i >= k - ind): #      sub[ind] = a[num + i] #     f(n, a, num+1+i, ind+1, k, sub) 

مثال العمل:

التعقيد هو نفسه كما في الطريقة السابقة.

5. إعطاء صفيف ترتيب تصاعدي بأرقام من $$$0$من قبل $$$n-1$، يلزم توليد جميع تبديلاته.

سوف نحل باستخدام العودية. الحل مشابه للحل السابق ، حيث لدينا قائمة مساعدة. هو في البداية صفر إذا كان $$$i$- مكان العنصر هو وحدة ثم العنصر $$$i$بالفعل في التقليب. لم يقل ما فعله:

 a = np.array(range(3)) n = a.shape[0] ind_mark = np.zeros(n) #   perm = -np.ones(n) #     def f(ind_mark, perm, ind, n): if ind == n: print (perm) else: for i in range(n): if not ind_mark[i]: #     ind_mark[i] = 1 #   perm[ind] = i f(ind_mark, perm, ind+1, n) #   -    ind_mark[i] = 0 

مثال العمل:

تعقيد هذه الخوارزمية هو $$$O (n ^ 2 * n!)$من الذاكرة - $$$O (n).$

الآن فكر في اثنين من الألغاز المثيرة للاهتمام لرموز الرمادي . باختصار ، هذه مجموعة من التسلسلات بنفس الطول ، حيث يختلف كل تسلسل عن جيرانه في فئة واحدة.

6. إنشاء جميع رموز الرمادي ثنائي الأبعاد طول ن.

فكرة حل هذه المشكلة رائعة ، ولكن إذا كنت لا تعرف الحل ، فقد يكون من الصعب جدًا التفكير فيه. ألاحظ أن عدد هذه التسلسلات هو $$$2 ^ n$.

سوف نحلها بشكل متكرر. لنفترض أننا أنشأنا جزءًا من هذه التسلسلات وأنهم يكمنون في بعض القائمة. إذا قمنا بتكرار مثل هذه القائمة وكتبناها بالترتيب العكسي ، فإن الترتيب الأخير في القائمة الأولى يتزامن مع التسلسل الأول في القائمة الثانية ، تتزامن القائمة قبل الأخيرة مع الثانية ، وما إلى ذلك. اجمع هذه القوائم في قائمة واحدة.

ما الذي يجب القيام به بحيث تختلف جميع التسلسلات في القائمة عن بعضها البعض في نفس الفئة؟ ضع وحدة واحدة في الأماكن المناسبة في عناصر القائمة الثانية للحصول على الرموز الرمادية.

من الصعب إدراك "بالأذن" ؛ سنصور تكرارات هذه الخوارزمية.

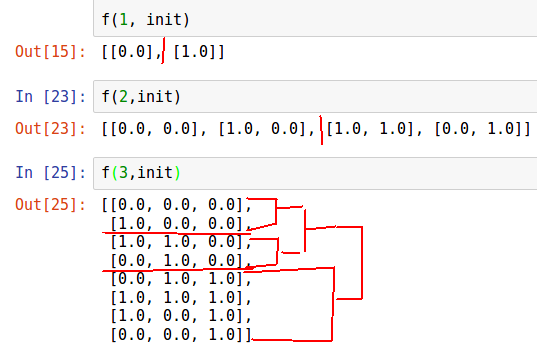
 n = 3 init = [list(np.zeros(n))] def f(n, init): for i in range(n): for j in range(2**i): init.append(list(init[2**i - j - 1])) init[-1][i] = 1.0 return init 

تعقيد هذه المهمة $$$O (n * 2 ^ n)$، من الذاكرة نفسها.

الآن دعونا نعقد المهمة.

7. قم بتوليد كافة الرموز الرمادية k ذات الأبعاد n.

من الواضح أن المهمة السابقة ليست سوى حالة خاصة لهذه المهمة. ومع ذلك ، بهذه الطريقة الجميلة التي تم بها حل المهمة السابقة ، لا يمكن حلها ؛ هنا من الضروري ترتيب التسلسل بالترتيب الصحيح. دعونا نحصل على مصفوفة ثنائية الأبعاد $$$k * n$. في البداية ، يحتوي السطر الأخير على وحدات ، والباقي يحتوي على أصفار. علاوة على ذلك ، في المصفوفة ، $$$-1$. هنا $$$1$و $$$-1$تختلف عن بعضها البعض في الاتجاه: $$$1$يشير $$$-1$يشير إلى أسفل. هام: في كل عمود يمكن أن يكون هناك عمود واحد فقط $$$1$أو $$$-1$وستكون الأعداد المتبقية أصفار.

الآن سوف نفهم كيف يمكن فرز هذه التسلسلات من أجل الحصول على رموز رمادية. ابدأ من النهاية لتحريك العنصر لأعلى.

في الخطوة التالية ، وصلنا إلى السقف. نكتب التسلسل الناتج. بعد الوصول إلى الحد الأقصى ، تحتاج إلى بدء العمل مع العمود التالي. تحتاج إلى البحث عنه من اليمين إلى اليسار ، وإذا وجدنا عمودًا يمكن تحريكه ، فإن جميع الأعمدة التي لم نتمكن من العمل معها ستتغير الأسهم في الاتجاه المعاكس بحيث يمكن نقلها مرة أخرى.

الآن يمكنك تحريك العمود الأول لأسفل. نقوم بتحريكه حتى يضرب الأرض. وهكذا ، حتى تصل جميع الأسهم إلى الأرض أو السقف ولا يتبقى أي أعمدة يمكن تحريكها.

ومع ذلك ، في إطار توفير الذاكرة ، سنقوم بحل هذه المشكلة باستخدام صفيفين أحاديين الطول $$$n$: في صفيف واحد ، ستكمن عناصر التسلسل نفسها ، وفي الاتجاه الآخر (الأسهم).

 n,k = 3,3 arr = np.zeros(n) direction = np.ones(n) #   ,    def k_dim_gray(n,k): #    print (arr) while True: ind = n-1 while ind >= 0: #    ,    if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1): direction[ind] = (direction[ind]+1)%2 else: break ind -= 1 #     ,     if ind < 0: break #    1 ,   1  arr[ind] += direction[ind]*2 - 1 print (arr) 

مثال العمل:

تعقيد الخوارزمية $$$O (n * k ^ n)$من الذاكرة - $$$O (n)$.

ثبت صحة هذه الخوارزمية عن طريق الاستقراء $$$n$، هنا لن أصف الأدلة.

في المقالة التالية ، سنقوم بتحليل مهام الديناميكيات.