🐀 👏🏻 🧔 حساب التكاملات المحددة: الخوارزميات الأساسية ⛹🏾 🧡 😿

الصورة
يصف هذا المنشور أبسط الطرق لحساب تكاملات دالات متغير واحد على قطعة ، تسمى أيضًا الصيغ التربيعية. عادةً ، يتم تنفيذ هذه الأساليب في المكتبات الرياضية القياسية مثل مكتبة GNU العلمية لـ C و SciPy لـ Python وغيرها. يهدف المنشور إلى توضيح كيفية عمل هذه الأساليب "تحت غطاء المحرك" ، ولفت الانتباه إلى بعض قضايا الدقة وأداء الخوارزميات. أود أيضًا أن أشير إلى علاقة الصيغ التربيعية وطرق التكامل العددي للمعادلات التفاضلية العادية ، والتي أود أن أكتب عنها منشورًا آخر.

تعريف التكامل

تكامل (وفقًا لـ Riemann) للدالة $f (x)$ على الجزء $[a؛ b]$ الحد التالي يسمى:

، د و ل ا

$\ int_a ^ bf (x) dx = \ lim _ {\ Delta x \ to 0} \ sum_ {i = 0} ^ {n-1} f (\ xi_i) (x_ {i + 1} - x_i) ، ~ ~ (1) دولا$

أين $\ Delta x = \ max \ lbrace x_ {i + 1} - x_i \ rbrace$ - دقة القسم ، $x_0 = دولا$ ، $x_n = b$ ، $\ xi_i$ - رقم تعسفي على القطعة $[x_i ؛ x_ {i + 1}]$ .

إذا كان تكامل الوظيفة موجودًا ، فإن القيمة الحدية هي نفسها بغض النظر عن القسم ، إذا كانت ستكون صغيرة بما يكفي.
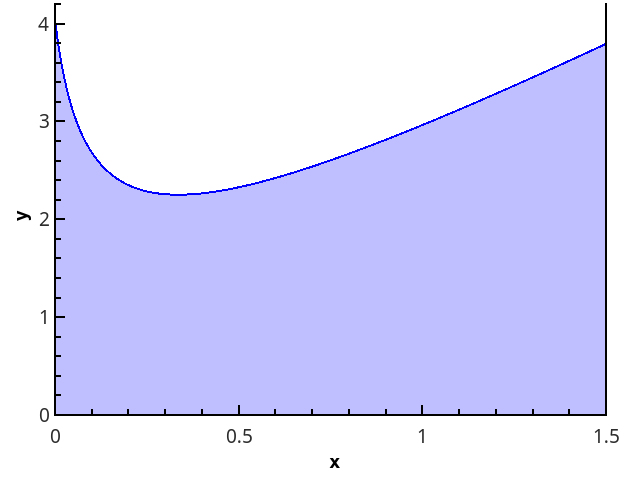
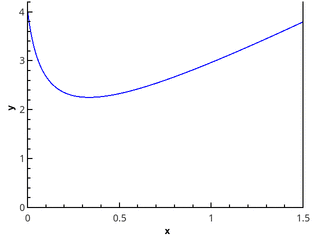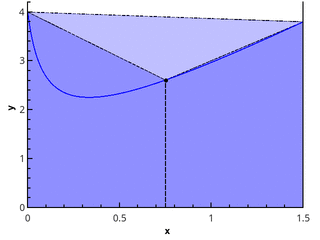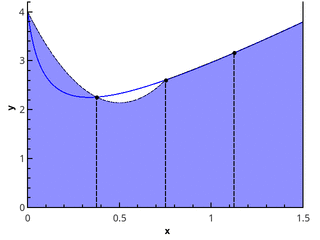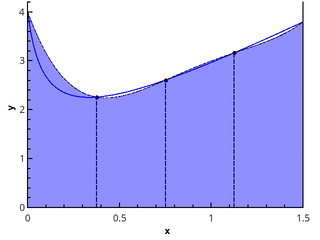
الصورة
التعريف الهندسي أكثر وضوحا - التكامل يساوي مساحة شبه منحرف منحني يحدها المحور 0 × ، الرسم البياني للدالة ، والخطوط المستقيمة x = a و x = b (المنطقة المعبأة في الشكل).

صيغ التربيع

يمكن إعادة كتابة تعريف التكامل (1) في النموذج

$I = \ int_a ^ b f (x) dx \ almost I_n = (b - a) \ sum_ {i = 0} ^ {n-1} w_i f (\ xi_i)، ~~ (2)$

أين $w_i$ - معاملات الترجيح ، التي يجب أن يساوي مجموعها 1 ، والمعاملات نفسها - تميل إلى الصفر مع زيادة العدد $n$ النقاط التي يتم فيها حساب الوظيفة.

التعبير (2) هو أساس جميع الصيغ التربيعية (أي صيغ الحساب التقريبي للتكامل). التحدي هو تحديد النقاط $\ lbrace \ xi_i \ rbrace$ والوزن $w_i$ بحيث يقترب المجموع على الجانب الأيمن من التكامل المطلوب بأكبر قدر ممكن من الدقة.

مهمة حسابية

مجموعة الوظائف $f (x)$ التي يوجد لها خوارزمية لحساب القيم في أي نقطة في الفاصل الزمني $[a؛ b]$ (أعني النقاط التي يمثلها رقم الفاصلة العائمة - لا توجد وظائف Dirichlet هناك!).

مطلوب للعثور على القيمة التقريبية للتكامل $\ int_a ^ b f (x) dx$ .
سيتم تنفيذ الحلول في Python 3.6.

للتحقق من الأساليب ، استخدم التكامل $\ int_0 ^ {3/2} \ left [2x + \ frac {1} {\ sqrt {x + 1/16}} \ right] dx = 17/4$ .

تقريب التقريب المستمر

تنشأ الصيغ التربيعية البسيطة المثالية من تطبيق التعبير (1) "في الجبين":

$I_n = \ sum_ {i = 0} ^ {n-1} f (\ xi_i) (x_ {i + 1} - x_i)$

لأن من طريقة قسمة قطعة على نقاط $\ lbrace x_i \ rbrace$ وحدد النقاط $\ lbrace \ xi_i \ rbrace$ لا تعتمد القيمة الحدية ، ثم نختارها بحيث يمكن حسابها بشكل ملائم - على سبيل المثال ، نأخذ القسم بشكل موحد ، ونقاط حساب الوظيفة نأخذ في الاعتبار الخيارات: 1) $\ xi_i = x_i$ ؛ 2) $\ xi_i = x_ {i + 1}$ ؛ 3) $\ xi_i = (x_i + x_ {i + 1}) / 2$ .

نحصل على طرق المستطيلات اليسرى والمستطيلات اليمنى والمستطيلات مع نقطة المنتصف على التوالي.

التنفيذ

def _rectangle_rule(func, a, b, nseg, frac): """  .""" dx = 1.0 * (b - a) / nseg sum = 0.0 xstart = a + frac * dx # 0 <= frac <= 1    , #    , #     dx for i in range(npoints): sum += func(xstart + i * dx) return sum * dx def left_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, nseg, 0.0) def right_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, npoints, 1.0) def midpoint_rectangle_rule(func, a, b, nseg): """    """ return _rectangle_rule(func, a, b, nseg, 0.5)

لتحليل أداء الصيغ التربيعية ، نقوم بإنشاء رسم بياني للخطأ في الإحداثيات "عدد النقاط هو الفرق بين النتيجة العددية والنتيجة الدقيقة."

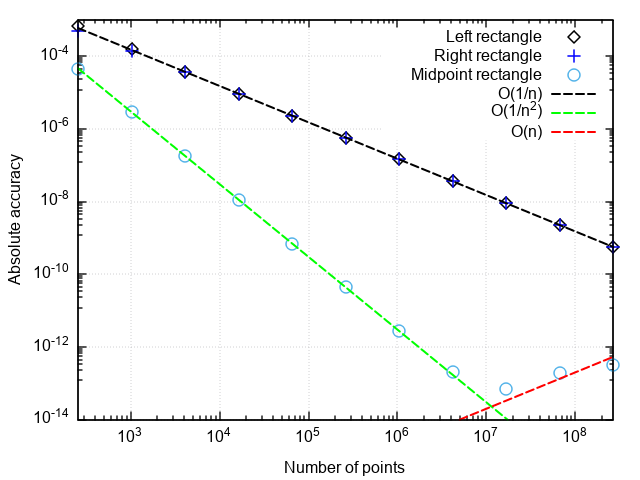
الصورة

ما يمكنك ملاحظته:

تكون الصيغة بنقطة المنتصف أكثر دقة من النقطة اليمنى أو اليسرى
يقع خطأ الصيغة مع نقطة المنتصف أسرع من الاثنين الآخرين
مع قسم صغير جدًا ، يبدأ خطأ الصيغة بنقطة المنتصف في الزيادة
ترتبط النقطتان الأوليان بحقيقة أن صيغة المستطيلات ذات نقطة المنتصف لها ترتيب تقريب ثانٍ ، أي $| I_n - I | = O (1 / n ^ 2)$ ، وصيغ المستطيلات اليمنى واليسرى هي الترتيب الأول ، أي $| I_n - I | = O (1 / n)$ .
ترتبط الزيادة في الخطأ أثناء طحن خطوة التكامل بزيادة في خطأ التقريب عند جمع عدد كبير من المصطلحات. ينمو هذا الخطأ مثل $| I_n - I | = O (1 / n)$ لا يسمح بالتكامل لتحقيق دقة الماكينة.
الخلاصة: إن طرق المستطيلات ذات النقاط اليمنى واليسرى ذات دقة منخفضة ، والتي تنمو أيضًا ببطء مع تحسين القسم. لذلك ، فهي منطقية فقط لأغراض العرض التوضيحي. تتميز طريقة المستطيلات ذات نقطة المنتصف بترتيب تقريبي أعلى ، مما يمنحها فرصة لاستخدامها في التطبيقات الحقيقية (المزيد عن ذلك أدناه).

التقريب الخطي المجزأ

الخطوة المنطقية التالية هي تقريب الدالة القابلة للتكامل في كل مقطع من الأقسام الفرعية بدالة خطية ، والتي تعطي صيغة التربيعية للرباعيات:

$I_n = \ sum_ {i = 0} ^ {n-1} \ frac {f (x_i) + f (x_ {i + 1})} {2} (x_ {i + 1} - x_i) ~~ ( 3)$

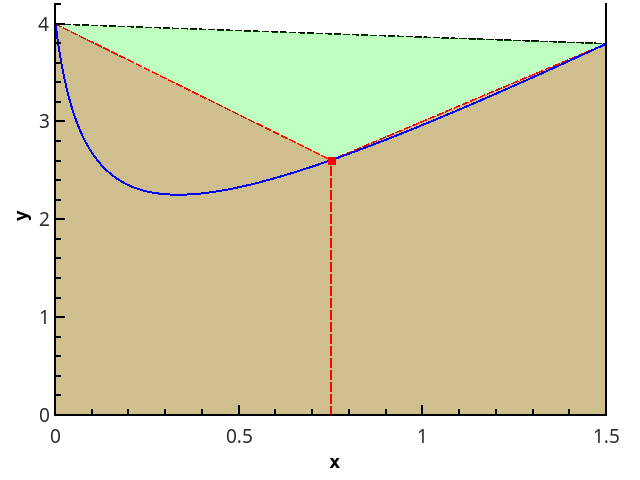
الصورة
رسم توضيحي للطريقة شبه المنحرفة لـ n = 1 و n = 2.

في حالة الشبكة الموحدة ، تكون أطوال جميع أجزاء التبليط متساوية ، والصيغة

$I_n = h \ left (\ frac {f (a) + f (b)} {2} + \ sum_ {i = 1} ^ {n-1} f (a + ih) \ right) ، ~ h = \ frac {ba} {n} ~~ (3a)$

التنفيذ

 def trapezoid_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" dx = 1.0 * (b - a) / nseg sum = 0.5 * (func(a) + func(b)) for i in range(1, nseg): sum += func(a + i * dx) return sum * dx

بعد أن رسمنا الخطأ مقابل عدد نقاط الانقسام ، نرى أن طريقة شبه المنحرف لها أيضًا ترتيب تقريب ثانٍ وتعطي عمومًا نتائج مختلفة قليلاً عن طريقة مستطيل نقطة المنتصف (فيما يلي ببساطة طريقة المستطيل).
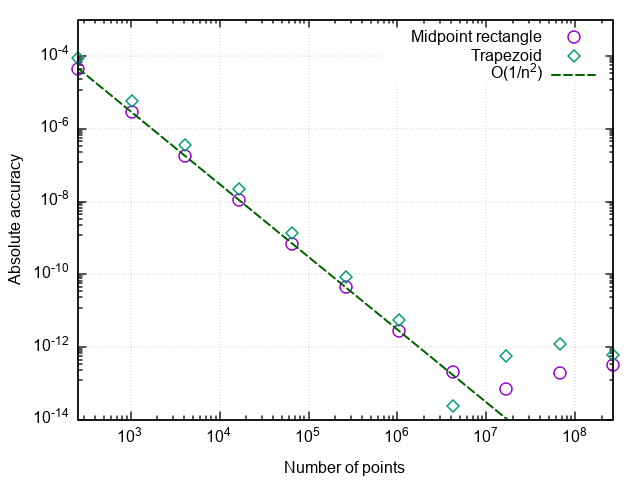
الصورة

مراقبة دقة الحساب

لا يعد تعيين عدد نقاط الانقسام كمعلمة إدخال أمرًا عمليًا للغاية ، نظرًا لأنه مطلوب عادةً لحساب التكامل ليس بكثافة قسم معينة ، ولكن مع وجود خطأ معين. إذا كان Integrand معروفًا مسبقًا ، فيمكننا تقدير الخطأ مقدمًا واختيار خطوة التكامل بحيث يتم تحقيق الدقة المحددة بالتأكيد. ولكن نادرًا ما يكون هذا هو الحال في الممارسة (وبشكل عام ، أليس من الأسهل ، مع وجود وظيفة معروفة في المستقبل ، دمج التكامل مقدمًا؟) ، لذلك ، من الضروري إجراء تعديل تلقائي للخطوة إلى خطأ معين.

كيفية تنفيذ ذلك؟ إحدى الطرق البسيطة لتقدير الخطأ - قاعدة رونج - الاختلاف في قيم التكاملات المحسوبة من النقطتين والنقطتين ، يعطي تقديرًا للخطأ: $\ Delta_ {2n} \ تقريبا | I_ {2n} - I_n |$ . طريقة شبه المنحرف أكثر ملاءمة لمضاعفة دقة التقسيم من طريقة المستطيلات بنقطة مركزية. عند الحساب بطريقة شبه المنحرف ، لمضاعفة عدد النقاط ، هناك حاجة إلى قيم جديدة للدالة فقط في منتصف أجزاء القسم السابق ، أي يمكن استخدام التقريب السابق للتكامل لحساب التالي.

ما هي طريقة المستطيل الأخرى؟

لا تتطلب طريقة المستطيل حساب قيم الدالة في نهايات المقطع. هذا يعني أنه يمكن استخدامه للوظائف التي لها ميزات قابلة للتكامل عند حواف المقطع (على سبيل المثال ، sin x / x أو x ^-1/2 من 0 إلى 1). لذلك ، ستعمل طريقة الاستقراء الموضحة أدناه بالطريقة نفسها تمامًا لطريقة المستطيل. الفرق من الطريقة شبه المنحرفة هو أنه عندما تنخفض الخطوة إلى النصف ، يتم تجاهل نتيجة الحسابات السابقة ، ومع ذلك ، يمكنك مضاعفة عدد النقاط ثلاث مرات ، ثم يمكن أيضًا استخدام القيمة السابقة للتكامل لحساب نقطة جديدة. يجب تعديل صيغ الاستقراء في هذه الحالة إلى نسبة مختلفة من خطوات التكامل.

من هنا نحصل على الكود التالي لطريقة شبه المنحرف مع تحكم دقيق:

 def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1): """  rtol -     nseg0 -    """ nseg = nseg0 old_ans = 0.0 dx = 1.0 * (b - a) / nseg ans = 0.5 * (func(a) + func(b)) for i in range(1, nseg): ans += func(a + i * dx) ans *= dx err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) #      #       nseg *= 2 err_est = abs(ans - old_ans) return ans

باستخدام هذا النهج ، لن يتم حساب Integrand عدة مرات عند نقطة واحدة ، ويتم استخدام جميع القيم المحسوبة للنتيجة النهائية.

ولكن هل من الممكن تحقيق دقة أعلى بنفس عدد حسابات الوظائف؟ اتضح أنه من الممكن ، هناك صيغ تعمل بدقة أكبر من طريقة شبه المنحرف على نفس الشبكة.

تقريب مكافئ مجزأ

الخطوة التالية هي تقريب الوظيفة باستخدام عناصر مكافئة. هذا يتطلب أن يكون عدد أجزاء القسم متساوًا ، ثم يمكن رسم القطع المكافئ من خلال ثلاث نقاط من النقاط مع الخراجات {( x ₀ = a ، x ₁ ، x ₂ ) ، ( x ₂ ، x ₃ ، x ₄ ) ، ... ، ( س _{ن -2} ، س _{ن -1} ، س _ن = ب )}.

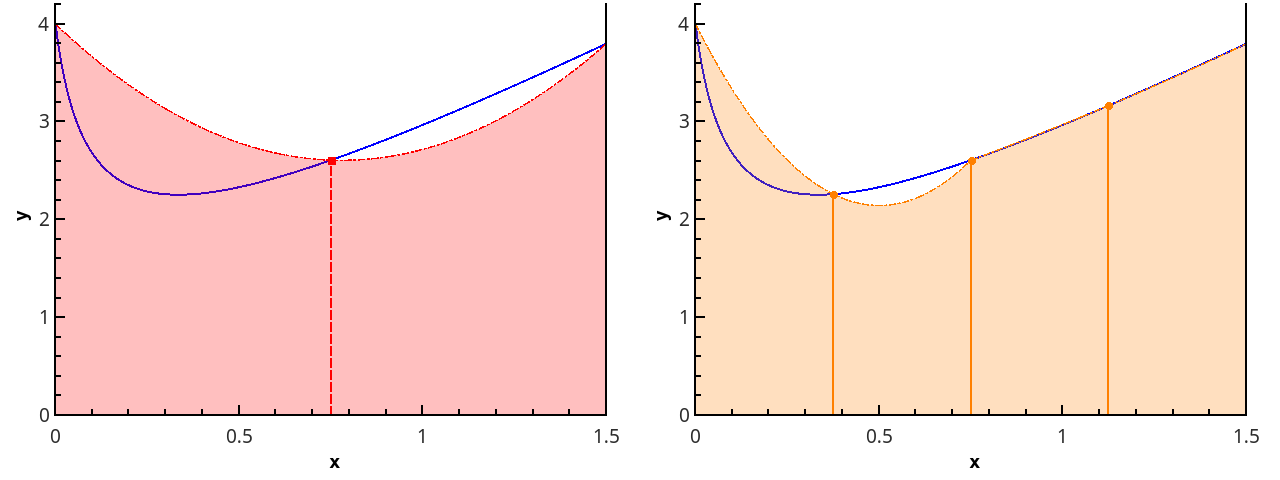
توضيح لتقريب مكافئ مجزأ عند 3 و 5 نقاط ( n = 2 و n = 3).

الاقتراب من تكامل الوظيفة في كل مقطع [ x _k ؛ x _{k +2} ] من خلال تكامل التقريب المكافئي في هذا الجزء مع مراعاة النقاط الموزعة بشكل موحد ( x _{k +1} = x _k + h ) ، نحصل على صيغة Simpson :

$I_ {Simps، n} = \ sum_ {i = 0} ^ {n / 2-1} \ frac {h} {3} [f (x_ {2i}) + 4f (x_ {2i + 1}) + f (x_ {2i + 2})] = \\ = \ frac {h} {3} [f (a) + 4f (a + h) + 2f (a + 2h) + ... + 4f (bh) + f (b)] ~~ (4)$

تعطي الصيغة (4) مباشرة تنفيذ "ساذج" لطريقة سيمبسون:

عنوان المفسد

 def simpson_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" if nseg%2 = 1: nseg += 1 dx = 1.0 * (b - a) / nseg sum = (func(a) + 4 * func(a + dx) + func(b)) for i in range(1, nseg / 2): sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx) return sum * dx / 3

لتقدير الخطأ ، يمكنك استخدام نفس الحساب للتكامل مع الخطوتين h و h / 2 - ولكن هنا تكمن المشكلة ، عند حساب التكامل بخطوة أصغر ، سيتعين تجاهل نتيجة الحساب السابق ، على الرغم من أن نصف حسابات الوظائف الجديدة ستكون في نفس النقاط كما كانت من قبل.

لحسن الحظ ، يمكنك تجنب إضاعة وقت الآلة إذا قمت بتطبيق طريقة Simpson بطريقة أكثر براعة. بعد إلقاء نظرة فاحصة ، نلاحظ أن التكامل بواسطة صيغة سيمبسون يمكن تمثيله من خلال تكاملين بواسطة الصيغة شبه المنحرفة بخطوات مختلفة. ويتجلى هذا بشكل أوضح في الحالة الأساسية لتقريب التكامل على ثلاث نقاط $(a، f_0)، ~ (a + h، f_1)، ~ (a + 2h، f_2)$ :

$I_ {Simps، 2} = \ frac {h} {3} (f_0 + 4f_1 + f_2) = \ frac {4} {3} h \ left (\ frac {f_0 + f_1} {2} + \ frac { f_1 + f_2} {2} \ right) - \ frac {1} {3} \ cdot2h \ frac {f_0 + f_2} {2} = \\ = \ frac {4I_ {trap، 2} - I_ {trap، 1 }} {3}$

وبالتالي ، إذا قمنا بتنفيذ إجراء تقليل الخطوة بمقدار النصف وتخزين الحسابين الأخيرين بطريقة شبه المنحرف ، يتم تنفيذ طريقة Simpson مع التحكم في الدقة بشكل أكثر كفاءة.

شيء من هذا القبيل ...

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #           nseg0 Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ ans = Quadrature.__restart(func, x0, x1, nseg0) old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = Quadrature.__double_nseg(func, x0, x1) err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0) new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans old_trapez_sum = new_trapez_sum new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans

قارن فعالية طريقة شبه المنحرف والقطع المكافئ:

 >>> import math >>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 65537 4.250000001385811 >>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 2049 4.2500000000490985

كما ترون ، مع كلتا الطريقتين يمكن الحصول على الإجابة بدقة عالية إلى حد ما ، ولكن عدد المكالمات إلى Integrand مختلف تمامًا - طريقة الترتيب الأعلى أكثر كفاءة 32 مرة!

من خلال رسم خطأ التكامل مقابل عدد الخطوات ، يمكننا التحقق من أن الترتيب التقريبي لصيغة سيمبسون هو أربعة ، أي خطأ تكامل رقمي $| I_ {Simps، n} - I | = O (1 / n ^ 4)$ (ويتم حساب تكاملات كثيرات الحدود المكعبة باستخدام هذه الصيغة حتى أخطاء التقريب لأي n > 0!).
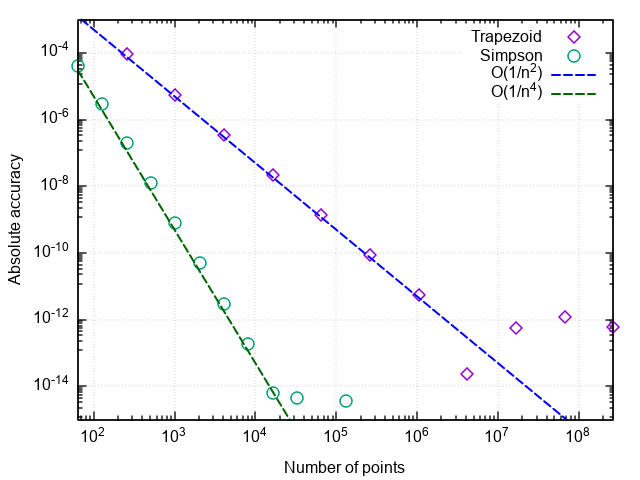
الصورة
وبالتالي ، تنشأ هذه الزيادة في الكفاءة بالمقارنة مع الصيغة شبه المنحرفة البسيطة.

ما هي الخطوة التالية؟

المنطق الإضافي لزيادة دقة الصيغ التربيعية مفهوم بشكل عام - إذا واصلنا تقريب الدالة مع كثيرات الحدود بدرجة أعلى من أي وقت مضى ، فإن تكامل كثيرات الحدود هذا سيقارب التكامل أكثر من الوظيفة الأصلية بشكل أكثر دقة. يسمى هذا النهج بناء صيغ نيوتن كوتس التربيعية . تُعرف الصيغ حتى 8 أوامر تقريب ، ولكن تظهر المصطلحات البديلة بين معاملات الترجيح w _i in (2) ، وتفقد الصيغ الاستقرار في الحسابات.

لنجرب الطريقة الأخرى. يتم تمثيل خطأ الصيغة التربيعية كسلسلة في سلطات خطوة التكامل h . خاصية ملحوظة للطريقة شبه المنحرفة (والمستطيلات ذات نقطة المنتصف!) هي أن هذه السلسلة تتكون من درجات متساوية فقط:

$I_ {trap، n} [f، a، b] = \ int_a ^ bf (x) dx + C_2h ^ 2 + C_4h ^ 4 + C_6h ^ 6 + ...، ~ h = \ frac {ba} {n } ~~~ (5)$

يعتمد استقراء ريتشاردسون على إيجاد تقاربات متتالية لهذا التوسع: بدلاً من تقريب التكامل مع كثير الحدود ، من التقريبات المحسوبة للتكامل $I (ح)$ يتم إنشاء تقريب متعدد الحدود ، والذي لـ h = 0 يجب أن يعطي أفضل تقريب للقيمة الحقيقية للتكامل.

إن توسيع خطأ التكامل في القوى الزوجية لخطوة التقسيم يسرع بشكل حاد من تقارب الاستقراء ، لأن لتقريب الترتيب 2 ن ، هناك حاجة فقط إلى قيم n للتكامل بواسطة طريقة شبه المنحرف.

إذا افترضنا أن كل مصطلح لاحق أقل من المصطلح السابق ، فيمكننا استبعاد درجات h بالتسلسل ، مع احتساب تقديرات تقريبية متكاملة مع خطوات مختلفة. نظرًا لأن التنفيذ أعلاه يسمح لنا بسهولة بتقسيم القسم إلى نصفين ، فمن المناسب النظر في الصيغ للخطوتين h و h / 2.

$I_ {trap، n} - I \ almost C_2h ^ 2؛ ~ I_ {trap، 2n} - I \ almost C_2 \ left (\ frac {h} {2} \ right) ^ 2$

من السهل إظهار أن استثناء الحد الأعلى لخطأ الصيغة شبه المنحرفة سيعطي صيغة سيمبسون بالضبط:

$I = I_ {trap، 2n} - C_2 \ left (\ frac {h} {2} \ right) ^ 2 + O (h ^ 4) \ تقريبا I_ {trap، 2n} - \ frac {I_ {trap، 2n} -I_ {trap، n}} {1-2 ^ 2} = I_ {Simps، 2n}$

بتكرار إجراء مماثل لصيغة سيمبسون ، نحصل على:

$I_ {Simps، 2n} - I \ almost C_4 \ left (\ frac {h} {2} \ right) ^ 4 ؛ ~ I_ {Simps، n} - I \ almost C_4h ^ 4$

$I = I_ {Simps، 2n} - C_4 \ left (\ frac {h} {2} \ right) ^ 4 + O (h ^ 6) \ تقريبا I_ {Simps، 2n} - \ frac {I_ {Simps، 2n} -I_ {Simps، n}} {1-2 ^ 4}$

إذا تابعت ، يلوح الجدول التالي:

2 ترتيب	4 ترتيب	6 ترتيب
أنا _0،0
أنا _1،0	أنا _1،1
أنا _2.0	أنا _2.1	أنا _2.2
...	...	...

يحتوي العمود الأول على التكاملات المحسوبة بطريقة شبه المنحرف. عند الانتقال من الصف العلوي لأسفل ، يصبح تقسيم المقطع ضعفيًا ، وعند الانتقال من العمود الأيسر إلى اليمين ، يزداد ترتيب تقريب التكامل (أي أن العمود الثاني يحتوي على التكاملات بطريقة Simpson ، وما إلى ذلك).

ترتبط عناصر الجدول ، كما يمكن استنتاجها من التوسع (5) ، بعلاقة التكرار:

$I_ {i، j} = I_ {i، j-1} - \ frac {I_ {i، j-1} -I_ {i-1، j-1}} {1- \ left (\ frac {h_ {ij}} {h_i} \ right) ^ 2} = I_ {i، j-1} - \ frac {I_ {i، j-1} -I_ {i-1، j-1}} {1-2 ^ {2j}} ~~~ (6)$

يمكن تقدير خطأ تقريب التكامل من اختلاف صيغ الطلبات المختلفة في سطر واحد ، أي

$\ Delta_ {i، j} \ almost I_ {i، j} - I_ {i، j-1}$

يسمى استخدام استقراء ريتشاردسون مع التكامل شبه المنحرف طريقة Romberg . إذا كانت طريقة Simpson تأخذ في الاعتبار القيمتين السابقتين من خلال الطريقة شبه المنحرفة ، فإن طريقة Romberg تستخدم جميع القيم المحسوبة مسبقًا بواسطة الطريقة شبه المنحرفة للحصول على تقدير أكثر دقة للتكامل.

التنفيذ

تتم إضافة طريقة إضافية إلى فئة Quadrature

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #          nseg0  Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True): """   nseg0 -     maxcol -   """ #   Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]] i = 0 maxcol = max(0, maxcol) ans = Itable[i][i] error_est = max(1, abs(ans)) while (error_est > abs(rtol * ans)): old_ans = ans i += 1 d = 4.0 ans_col = min(i, maxcol) Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1)) for j in range(0, ans_col): diff = Itable[i][j] - Itable[i - 1][j] Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0) d *= 4.0 ans = Itable[i][ans_col] if (maxcol <= 1): #       error_est = abs(ans - Itable[i - 1][-1]) elif (i > maxcol): error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)]) else: error_est = abs(ans - Itable[i - 1][i - 1]) print("Total function calls: " + str(Quadrature.__ncalls)) return ans

دعونا نتحقق من كيفية عمل التقريب عالي الترتيب:

 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) #  Total function calls: 65537 4.250000001385811 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) #  Total function calls: 2049 4.2500000000490985 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4) Total function calls: 257 4.250000001644076

نحن مقتنعون أنه بالمقارنة مع طريقة القطع المكافئ ، انخفض عدد المكالمات إلى المكالمة بمقدار 8 مرات أخرى. مع زيادة أخرى في الدقة المطلوبة ، تصبح مزايا طريقة Romberg أكثر وضوحًا:
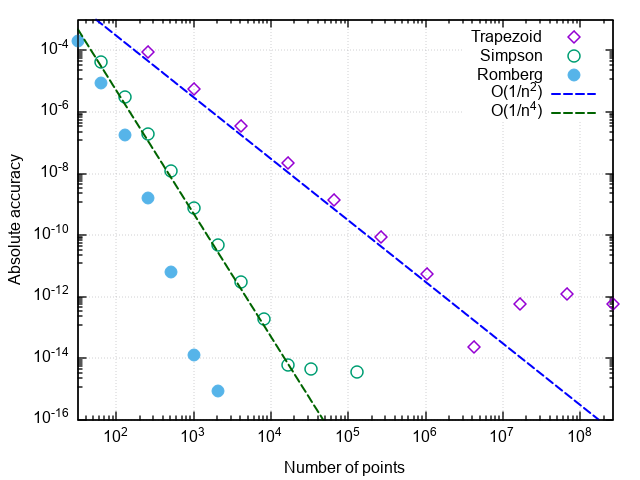
الصورة

بعض الملاحظات

ملاحظة 1. يميز عدد استدعاءات الدوال في هذه المشاكل عدد المبالغ عند حساب التكامل. لا يؤدي تقليل عدد حسابات Integrand إلى توفير موارد الحوسبة فقط (على الرغم من أن هذا هو الحال أيضًا مع تنفيذ أكثر تحسينًا) ، ولكنه يقلل أيضًا من تأثير أخطاء التقريب على النتيجة. لذلك ، عندما تحاول حساب تكامل وظيفة الاختبار ، تتجمد طريقة شبه المنحرف عندما تحاول تحقيق دقة نسبية من 5 × ^10-15 ، طريقة القطع المكافئ - مع الدقة المطلوبة 2 × 10 ^-16 (وهو الحد الأقصى لأرقام الدقة المزدوجة) ، وتتوافق طريقة رومبرغ مع الحساب اختبار جزء لا يتجزأ من دقة الجهاز (مع خطأ بت منخفض). أي أنه لا يتم فقط زيادة دقة التكامل لعدد معين من استدعاءات الوظائف ، ولكن أيضًا الحد الأقصى من الدقة القابلة للتحقيق لحساب التكامل.

ملاحظة 2. إذا كانت الطريقة تتقارب عند تحديد دقة معينة ، فإن هذا لا يعني أن القيمة المحسوبة للتكامل لها نفس الدقة. بادئ ذي بدء ، ينطبق هذا على الحالات التي يكون فيها الخطأ المحدد قريبًا من دقة الماكينة.

ملاحظة 3. على الرغم من أن طريقة Romberg لعدد من الوظائف تعمل بطريقة سحرية تقريبًا ، إلا أنها تفترض أن Integrand قد ربطت مشتقات من أوامر عالية. هذا يعني أنه بالنسبة للوظائف ذات الخلل أو الفواصل ، فقد يتبين أنها أسوأ من الطرق البسيطة. على سبيل المثال ، قم بدمج f ( x ) = | x |:

 >>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5) Total function calls: 9 5.0 >>> Quadrature.simpson(abs, -1, 3, rtol=1e-5) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3) Total function calls: 33 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4) Total function calls: 33 5.000001383269357

ملاحظة 4. قد يبدو أنه كلما ارتفع ترتيب التقريب ، كان ذلك أفضل. في الواقع ، من الأفضل تحديد عدد الأعمدة في جدول Romberg بـ 4-6. لفهم هذا ، انظر إلى الصيغة (6). الحد الثاني هو الفرق بين عنصرين متتاليين من العمود j -1 مقسومًا على حوالي 4 ^j . لأن يحتوي العمود j -th على تقديرات تكاملية للترتيب 2 j ، ثم يكون الفرق نفسه بترتيب (1 / n _i ) ^{2 j} ~ 4 ^{- ij} . مع مراعاة القسمة ، يتم الحصول على ~ 4 ^{- ( i +1) j} ~ 4 ^{- j ²} . على سبيل المثال بالنسبة لـ j ~ 7 ، يفقد المصطلح الثاني في (6) الدقة بعد تقليل الطلبات عند إضافة أرقام الفاصلة العائمة ، ويمكن أن تؤدي زيادة ترتيب التقريب إلى تراكم أخطاء التقريب.

ملاحظة 5. يمكن للأطراف المهتمة استخدام الطرق الموصوفة لإيجاد التكامل من أجل المصلحة. $\ int_0 ^ 1 \ sqrt {x} \ sin {x} dx$ وما يعادله $\ int_0 ^ 1 2t ^ 2 \ sin {t ^ 2} dt$ . كما يقولون ، أشعر بالفرق.

الخلاصة

يتم تقديم وصف وتنفيذ الأساليب الأساسية للتكامل العددي للوظائف على شبكة موحدة. لقد تم شرح كيف ، باستخدام تعديل بسيط ، للحصول على فئة الصيغ التربيعية باستخدام طريقة Romberg على أساس طريقة شبه المنحرف ، والتي تسرع بشكل كبير من تقارب التكامل العددي. تعمل الطريقة بشكل جيد لدمج الوظائف "العادية" ، أي تتفاوت بشكل ضعيف على فاصل التكامل ، ولا توجد فراغات عند حواف الجزء (انظر الملاحظة 5) ، والتذبذبات السريعة ، إلخ.

( [3] — C++).

.. , .. . . .: . 1989.
J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
WH Press, SA Teukolsky, WT Vetterling, BP Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.

حساب التكاملات المحددة: الخوارزميات الأساسية

تعريف التكامل

صيغ التربيع

مهمة حسابية

تقريب التقريب المستمر

التقريب الخطي المجزأ

مراقبة دقة الحساب

تقريب مكافئ مجزأ

ما هي الخطوة التالية؟

بعض الملاحظات

الخلاصة

More articles: