عند فتح المقهى الخاص بك ، ترغب في معرفة إجابة السؤال التالي: "أين المقهى الآخر الأقرب إلى هذه النقطة؟" ستساعدك هذه المعلومات على فهم منافسيك بشكل أفضل.
هذا مثال على مشكلة البحث عن "
أقرب جار " ، والتي تتم دراستها على نطاق واسع في علوم الكمبيوتر. بالنظر إلى مجموعة من المعلومات ونقطة جديدة ، وتحتاج إلى معرفة أي نقطة من النقاط الموجودة ستكون أقرب؟ ينشأ مثل هذا السؤال في العديد من المواقف اليومية في مجالات مثل أبحاث الجينوم والبحث عن الصور وتوصيات Spotify.
ولكن ، على عكس مثال المقهى ، غالبًا ما تكون الأسئلة حول أقرب جار معقدة جدًا. على مدى العقود القليلة الماضية ، شرعت أعظم العقول بين علماء الكمبيوتر في إيجاد أفضل الطرق لحل هذه المشكلة. على وجه الخصوص ، حاولوا التعامل مع المضاعفات الناشئة عن حقيقة أنه في مجموعات البيانات المختلفة يمكن أن يكون هناك تعريفات مختلفة جدًا لـ "قرب" النقاط من بعضها البعض.
والآن ، توصل فريق من علماء الكمبيوتر إلى طريقة جديدة تمامًا لحل مشكلة العثور على أقرب جار. في
زوج من الأوراق ، وصف خمسة علماء بالتفصيل الطريقة الأولى المعممة لحل مشكلة العثور على أقرب جار للبيانات المعقدة.
قال
بيتر إنديك ، أخصائي تكنولوجيا المعلومات في معهد ماساتشوستس للتكنولوجيا ، وهو شخصية مؤثرة في مجال التطورات المتعلقة بهذه المهمة: "هذه هي النتيجة الأولى التي تغطي مجموعة واسعة من المساحات باستخدام تقنية خوارزمية واحدة".
فرق المسافة
نحن ملتزمون للغاية بالطريقة الوحيدة لتحديد المسافة بحيث يسهل إغفال إمكانية وجود طرق أخرى. عادة نقيس المسافة على أنها إقليدية - كخط مستقيم بين نقطتين. ومع ذلك ، هناك حالات تجعل التعاريف الأخرى أكثر منطقية. على سبيل المثال ، تجعلك
مسافة مانهاتن تدور 90 درجة ، كما لو كنت تتحرك على طول شبكة مستطيلة من الطرق. لقياس مسافة يمكن أن تكون 5 كيلومترات في خط مستقيم ، قد تحتاج إلى عبور المدينة 3 كم في اتجاه واحد ثم 4 أخرى في الاتجاه الآخر.
من الممكن أيضًا التحدث عن مسافات ليست بالمعنى الجغرافي. ما هي المسافة بين شخصين في شبكة اجتماعية ، أو فيلمين ، أو جينومين؟ في هذه الأمثلة ، تشير المسافة إلى درجة التشابه.
هناك العشرات من مقاييس المسافة ، كل منها مناسب لمهمة محددة. خذ ، على سبيل المثال ، جينومين. يقارنهم علماء الأحياء باستخدام "
مسافة Levenshtein " أو مسافة التحرير. مسافة التحرير بين تسلسلين للجينوم هي عدد الإضافات والحذف والإدخالات والبدائل اللازمة لتحويل أحدهما إلى آخر.
تحرير المسافة والمسافة الإقليدية هما مفهومان مختلفان للمسافة ، ومن المستحيل اختزال أحدهما إلى الآخر. يوجد هذا التعارض في العديد من أزواج مقاييس المسافة ، وهو عقبة أمام علماء الكمبيوتر الذين يحاولون تطوير خوارزميات للعثور على أقرب جار. وهذا يعني أن الخوارزمية التي تعمل لنوع من المسافة لن تعمل مع نوع آخر - بتعبير أدق ، كانت كذلك حتى الآن ، حتى ظهر نوع جديد من البحث.
الكسندر اندونيمربع الدائرة
النهج القياسي لإيجاد أقرب جار هو تقسيم البيانات الموجودة إلى مجموعات فرعية. إذا كانت بياناتك ، على سبيل المثال ، تصف موقع الأبقار في المراعي ، فيمكنك عندئذ وضع كل منها في دائرة. ثم نضع بقرة جديدة على المرج ونطرح السؤال التالي: أي دائرة تقع فيها؟ من المضمون عمليًا أن أقرب جار للبقرة الجديدة سيكون في نفس الدائرة.
ثم كرر العملية. تقسيم الدوائر إلى دوائر فرعية ، وتقسيم هذه الخلايا بشكل أكبر ، وهكذا. ونتيجة لذلك ، هناك خلية ذات نقطتين فقط: القائمة والجديدة. ستكون هذه النقطة الحالية أقرب جار لك.
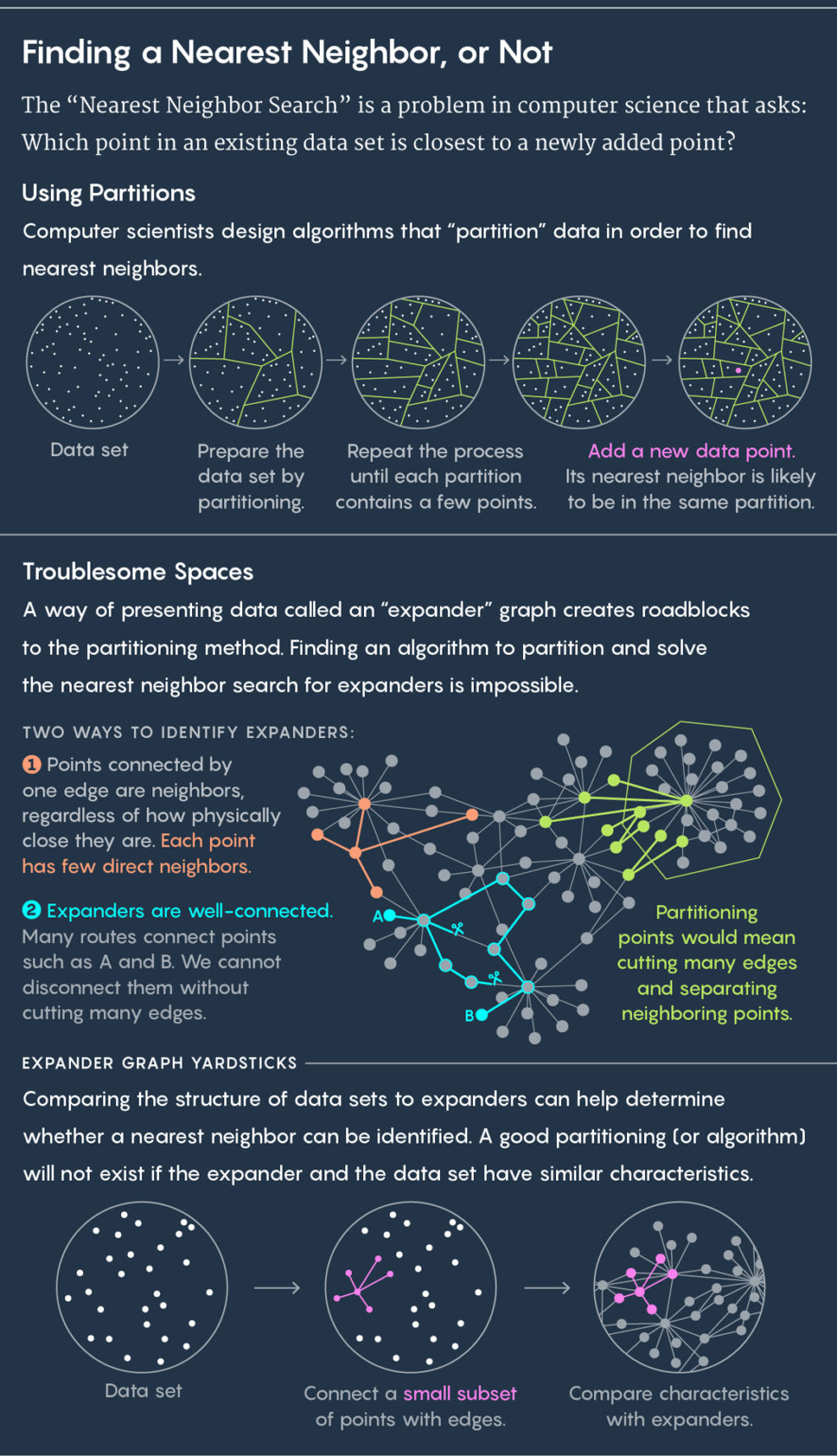أعلاه هو تقسيم البيانات إلى خلايا. أدناه استخدام الرسم البياني التمديد.الخوارزميات ترسم الخلايا ، والخوارزميات الجيدة ترسمها بسرعة وجيدة - أي أنه لا يوجد وضع تسقط فيه بقرة جديدة في دائرة وينتهي أقرب جار لها في دائرة أخرى. قالت
إيليا رازينشتين ،
أخصائية علوم الكمبيوتر في مايكروسوفت للأبحاث ، المؤلفة المشاركة في العمل الجديد ، الذي شارك فيه
ألكسندر أندوني من جامعة كولومبيا: "نريد أن تظهر النقاط القريبة في هذه الخلايا في كثير من الأحيان في نفس محرك الأقراص مع بعضها البعض ، وأن تكون
المسافات البعيدة نادرة".
وعساف ناعور من برينستون
وألكسندر نيكولوف من جامعة تورنتو
وإريك وينجارتن من جامعة كولومبيا.
لسنوات عديدة ، توصل علماء الكمبيوتر إلى خوارزميات مختلفة لرسم مثل هذه الخلايا. بالنسبة للبيانات الصغيرة - مثل تحديد نقطة واحدة بعدد صغير من القيم ، على سبيل المثال ، موقع بقرة في مرعى - تنشئ الخوارزميات ما يسمى "
مخططات Voronoi " التي تجيب بدقة على السؤال المتعلق بأقرب جار.
بالنسبة للبيانات متعددة الأبعاد ، حيث يمكن تحديد نقطة واحدة بمئات أو آلاف القيم ، تتطلب الرسوم البيانية Voronoi الكثير من قوة الحوسبة. وبدلاً من ذلك ، يرسم المبرمجون الخلايا باستخدام "
التجزئة الحساسة محليًا "
، التي وصفها Indik و Rajiv Motwani لأول
مرة في عام 1998. تقوم خوارزميات LF برسم الخلايا بشكل عشوائي. لذلك ، يعملون بشكل أسرع ، ولكن بشكل أقل دقة - بدلاً من العثور على أقرب جار بالضبط ، يضمنون أن النقطة لا تقع أبعد من مسافة معينة من أقرب جار حقيقي. يمكن تخيل ذلك كتوصية فيلم Netflix ، وهي ليست مثالية ، ولكنها جيدة بما يكفي.
منذ أواخر التسعينيات ، توصل علماء الكمبيوتر إلى خوارزميات LF التي توفر حلولًا تقريبية لمهمة العثور على أقرب جار لمقاييس المسافة المحددة. كانت الخوارزميات متخصصة للغاية ، ولا يمكن استخدام الخوارزمية التي تم تطويرها لمقياس مسافة واحدة لمقياس آخر.
"يمكنك التوصل إلى خوارزمية فعالة جدًا لمسافة الإقليدية أو مانهاتن لبعض الحالات المحددة. ولكن لم يكن لدينا خوارزمية عملت على فئة كبيرة من المسافات "، قال إنديك.
نظرًا لعدم إمكانية استخدام الخوارزميات التي تعمل بمقياس واحد لمقياس آخر ، توصل المبرمجون إلى إستراتيجية حل بديل. من خلال عملية تسمى "التضمين" ، فرضوا مقياسًا لم يكن لديهم خوارزمية جيدة عليه ، على المقياس الذي كان عليه. ومع ذلك ، كانت مراسلات المقاييس غير دقيقة عادة - شيء مثل ربط مربع في حفرة مستديرة. في بعض الحالات ، لم يعمل التضمين على الإطلاق. كان من الضروري إيجاد طريقة عالمية للإجابة على السؤال حول أقرب جار.
ايليا رازينشتيننتيجة غير متوقعة
في عمل جديد ، تخلى العلماء عن البحث عن خوارزميات خاصة. بدلاً من ذلك ، سألوا سؤالاً أوسع: ما الذي يمنع تطوير خوارزمية على مقياس مسافة معينة؟
قرروا أن الوضع غير السار المرتبط بالرسم البياني
المتوسع ، أو
الموسع ، هو السبب. الموسع هو نوع خاص من الرسم البياني ، مجموعة من النقاط المتصلة بالحواف. الرسوم البيانية لها قياس المسافة الخاصة بهم. المسافة بين نقطتين من الرسم البياني هي الحد الأدنى لعدد الخطوط اللازمة للانتقال من نقطة إلى أخرى. يمكنك أن تتخيل رسمًا بيانيًا يمثل الروابط بين الأشخاص في الشبكات الاجتماعية ، ومن ثم ستكون المسافة بين الأشخاص مساوية لعدد الاتصالات التي تفصل بينهم. على سبيل المثال ، إذا كان لدى جوليان مور صديق لديه صديق لديه كيفين بيكون صديقه ، فإن المسافة من مور إلى بيكون هي ثلاثة.
الموسع هو نوع خاص من الرسوم البيانية يحتوي على خاصيتين ، للوهلة الأولى ، خصائص متضاربة. لديها اتصال عالي ، أي أنه لا يمكن فصل نقطتين دون قطع عدة حواف. في الوقت نفسه ، ترتبط معظم النقاط بعدد صغير جدًا من النقاط الأخرى. وبسبب هذا ، فإن معظم النقاط بعيدة عن بعضها البعض.
مزيج فريد من هذه الخصائص - اتصال جيد وعدد قليل من الحواف - يؤدي إلى حقيقة أنه في المتوسعون من المستحيل إجراء بحث سريع عن أقرب جار. أي محاولات لتقسيمها إلى خلايا ستفصل النقاط التي تقع بالقرب من بعضها البعض.
قال وينجارتن ، مؤلف مشارك في العمل: "إن أي طريقة لقطع الموسع إلى قسمين تتطلب قطع أضلاع متعددة ، مما يقسم العديد من القمم المتقاربة".
بحلول صيف عام 2016 ، عرف Andoni و Nyokolov و Rasenstein و Vanguarten أنه بالنسبة للمتوسعين ، لا يمكن للمرء أن يتوصل إلى خوارزمية جيدة للعثور على أقرب جار. لكنهم أرادوا إثبات أنه من المستحيل إنشاء مثل هذه الخوارزميات للعديد من مقاييس المسافة الأخرى - المقاييس ، عند البحث عن خوارزميات جيدة توصل علماء الكمبيوتر إلى طريق مسدود فيها.
للعثور على دليل على استحالة مثل هذه الخوارزميات ، كانوا بحاجة إلى إيجاد طريقة لتضمين مقياس المتوسع في مقاييس المسافة الأخرى. باستخدام هذه الطريقة ، يمكنهم تحديد أن المقاييس الأخرى لها خصائص مشابهة لخصائص الموسعة ، مما يمنعها من إنشاء خوارزميات جيدة.
إريك وينجارتنذهب أربعة علماء كمبيوتر إلى عساف ناورو ، عالم رياضيات من جامعة برينستون ، والذي كان عمله السابق مناسبًا تمامًا لموضوع المتوسع. لقد طلبوا منه المساعدة في إثبات أن المتوسع يمكن تضمينه في أنواع مختلفة من المقاييس. عاد ناعور بسرعة بإجابة - ولكن ليس الجواب الذي توقعوه منه.
وقال أندوني: "طلبنا من عساف مساعدتنا في هذا البيان ، وأثبت العكس".
أثبت ناعور أن الموسعات لا تتناسب مع فئة كبيرة من مقاييس المسافة المعروفة باسم "
المساحات المعيارية " (والتي تتضمن أيضًا مقاييس مثل مساحات الإقليدية ومانهاتن). استنادًا إلى أدلة ناعور ، اتبع العلماء السلسلة المنطقية التالية: إذا لم تتناسب المتوسعات مع مقياس المسافة ، فيجب أن تكون هناك طريقة جيدة لكسرها إلى خلايا (نظرًا لأن خصائص المتوسع هي العائق الوحيد لهذا ، كما أثبتوا ذلك). لذلك ، يجب أن تكون هناك خوارزمية جيدة للعثور على أقرب جار - حتى لو لم يجدها أحد حتى الآن.
نشر خمسة باحثين نتائجهم في
ورقة أكملوها في نوفمبر وحملوها في أبريل. وأعقبه عمل ثانٍ ، أكملوه هذا العام
ونشره في أغسطس. استخدموا فيه المعلومات التي تم الحصول عليها عند كتابة العمل الأول للعثور على خوارزمية سريعة للعثور على أقرب جار للمساحات المعيارية.
قال وينجارتن: "أظهر العمل الأول وجود طريقة لتقسيم المقياس إلى قسمين ، ولكن لم تكن هناك وصفة لكيفية القيام بذلك بسرعة". "في العمل الثاني ، نقول أن هناك طريقة لفصل النقاط ، بالإضافة إلى ذلك ، يمكن أن يتم هذا الفصل باستخدام خوارزميات سريعة."
ونتيجة لذلك ، تعمل الأعمال الجديدة لأول مرة على تعميم البحث عن أقرب جار في البيانات متعددة الأبعاد. بدلاً من تطوير خوارزميات متخصصة لمقاييس محددة ، يمتلك المبرمجون نهجًا عالميًا للعثور على الخوارزميات.
قال وينجارتن: "هذه طريقة منظمة لتطوير خوارزميات للعثور على أقرب جار في أي من مقاييس المسافة التي تحتاجها".