لقد كافحت مع إغراء تسمية المقالة بشيء مثل "عدم الكفاءة المرعب لخوارزميات STL" - كما تعلمون ، لمجرد التدريب على فن إنشاء عناوين مبهرجة. ولكن مع ذلك ، قرر البقاء ضمن حدود الآداب - من الأفضل الحصول على تعليقات من القراء على محتوى المقالة بدلاً من السخط على اسمه الكبير.
عند هذه النقطة ، سأفترض أنك تعرف القليل من C ++ و STL ، كما ستهتم بالخوارزميات المستخدمة في التعليمات البرمجية وتعقيدها وصلتها بالمهام.
الخوارزميات
إحدى النصائح المعروفة جيدًا التي يمكنك سماعها من مجتمع مطوري C ++ الحديث هي عدم إيجاد دراجات ، ولكن استخدام خوارزميات من المكتبة القياسية. هذه نصيحة جيدة. هذه الخوارزميات آمنة وسريعة ومختبرة على مر السنين. أنا أيضا كثيرا ما أسدي المشورة بشأن تطبيقها.
في كل مرة تريد كتابة عنوان آخر - يجب أن تتذكر أولاً ما إذا كان هناك شيء في STL (أو تعزيز) يحل هذه المشكلة بالفعل في سطر واحد. إذا كان هناك ، فمن الأفضل غالبًا استخدام هذا. ومع ذلك ، في هذه الحالة ، يجب أن نفهم أيضًا نوع الخوارزمية الكامنة وراء استدعاء الوظيفة القياسية ، وما هي خصائصها وحدودها.
عادة ، إذا كانت مشكلتنا تتطابق تمامًا مع وصف الخوارزمية من STL ، فسيكون من الجيد أخذها وتطبيقها "جبهته". المشكلة الوحيدة هي أن البيانات لا يتم تخزينها دائمًا بالشكل الذي تريد الخوارزمية المنفذة في المكتبة القياسية استلامها. ثم قد تكون لدينا فكرة تحويل البيانات أولاً ، ثم بعد ذلك نطبق نفس الخوارزمية. حسنًا ، كما تعلم ، مثل تلك النكتة الحسابية "أخمد الحريق من الغلاية. تم تخفيض المهمة إلى المهمة السابقة ".
تقاطع المجموعات
تخيل أننا نحاول كتابة أداة لمبرمجي C ++ التي ستعثر على كل lambdas في الشفرة مع التقاط جميع المتغيرات الافتراضية ([=] و [&]) وعرض نصائح لتحويلها إلى lambdas مع قائمة محددة من المتغيرات الملتقطة. شيء من هذا القبيل:
std::partition(begin(elements), end(elements), [=] (auto element) {
في عملية تحليل الملف باستخدام الشفرة ، سيتعين علينا تخزين مجموعة المتغيرات في مكان ما في النطاق الحالي والمحيط ، وإذا تم الكشف عن لامدا مع التقاط جميع المتغيرات ، قارن بين هاتين المجموعتين وإسداء المشورة بشأن تحويلها.
مجموعة واحدة مع متغيرات في النطاق الأصلي ، ومجموعة أخرى مع متغيرات داخل لامدا. لتكوين النصيحة ، يحتاج المطور فقط إلى العثور على تقاطعهم. وهذا هو الحال عندما يكون وصف الخوارزمية من STL مثاليًا للمهمة: يأخذ
std :: set_intersection مجموعتين ويعيد تقاطعهما. الخوارزمية جميلة في بساطتها. يستغرق الأمر مجموعتين مفروشتين ويمر عبرهما بالتوازي:
- إذا كان العنصر الحالي في المجموعة الأولى مطابقًا للعنصر الحالي في المجموعة الثانية - أضفه إلى النتيجة وانتقل إلى العناصر التالية في كلتا المجموعتين
- إذا كان العنصر الحالي في المجموعة الأولى أقل من العنصر الحالي في المجموعة الثانية ، فانتقل إلى العنصر التالي في المجموعة الأولى
- إذا كان العنصر الحالي في المجموعة الأولى أكبر من العنصر الحالي في المجموعة الثانية ، فانتقل إلى العنصر التالي في المجموعة الثانية
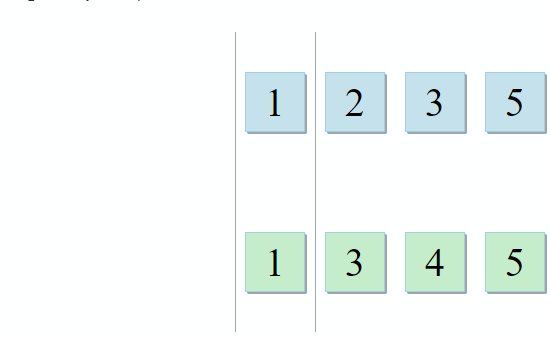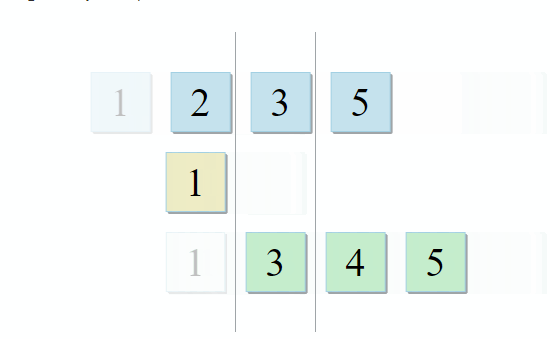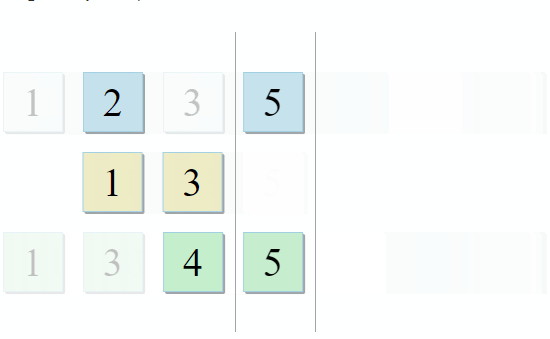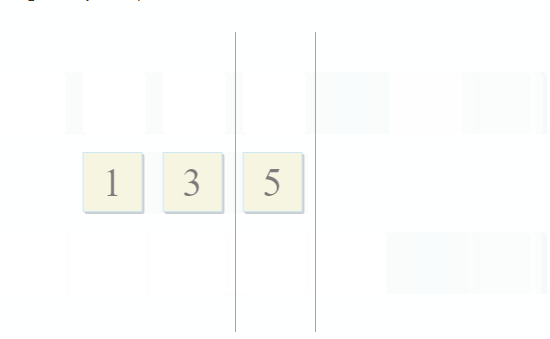
مع كل خطوة من الخوارزمية ، نتحرك على طول المجموعة الأولى أو الثانية أو كلتيهما ، مما يعني أن تعقيد هذه الخوارزمية سيكون خطيًا - O (m + n) ، حيث n و m هي أحجام المجموعات.
بسيطة وفعالة. ولكن هذا فقط حتى الآن يتم فرز مجموعات الإدخال.
الفرز
المشكلة هي أنه ، بشكل عام ، لا يتم فرز المجموعات. في حالتنا الخاصة ، من الملائم تخزين المتغيرات في بنية بيانات تشبه المكدس عن طريق إضافة متغيرات إلى مستوى المكدس التالي عند إدخال نطاق متداخل وإزالتها من المكدس عند مغادرة هذا النطاق.
هذا يعني أنه لن يتم فرز المتغيرات حسب الاسم ولا يمكننا استخدام std :: set_intersection مباشرة في مجموعاتها. نظرًا لأن std :: set_intersection تتطلب مجموعات مرتبة تمامًا عند الإدخال ، فقد تنشأ الفكرة (وغالبًا ما رأيت هذا النهج في المشاريع الحقيقية) لفرز المجموعات قبل استدعاء وظيفة المكتبة.
سيؤدي التصنيف في هذه الحالة إلى القضاء على فكرة استخدام مكدس لتخزين المتغيرات وفقًا لنطاقها ، ولكن لا يزال هذا ممكنًا:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_1(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { std::sort(first1, last1); std::sort(first2, last2); return std::set_intersection(first1, last1, first2, last2, dest); }
ما هو تعقيد الخوارزمية الناتجة؟ شيء مثل O (n log n + m log m + n + m) هو تعقيد شبه خطي.
فرز أقل
ألا يمكننا استخدام الفرز؟ نستطيع ، لماذا لا. سنبحث فقط عن كل عنصر من المجموعة الأولى في البحث الخطي الثاني. نحصل على التعقيد O (n * m). كما رأيت هذا النهج في المشاريع الحقيقية في كثير من الأحيان.
بدلاً من خيار "فرز كل شيء" و "عدم فرز أي شيء" ، يمكننا محاولة العثور على Zen والانتقال إلى الطريق الثالث - فرز مجموعة واحدة فقط. إذا تم فرز إحدى المجموعات ، ولكن الثانية لم يتم ترتيبها ، فيمكننا تكرار عناصر المجموعة غير المصنفة واحدة في كل مرة والبحث عنها في البحث الثنائي الذي تم فرزه.
سيكون تعقيد هذه الخوارزمية O (n log n) لفرز المجموعة الأولى و O (m log n) للبحث والتدقيق. في المجموع ، نحصل على التعقيد O ((n + m) log n).
إذا قررنا فرز مجموعة أخرى من المجموعات ، نحصل على التعقيد O ((n + m) log m). كما تفهم ، سيكون من المنطقي فرز مجموعة أصغر هنا للحصول على التعقيد النهائي لسجل O ((m + n) (min (m، n))
سيبدو التنفيذ كما يلي:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_2(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_2(first2, last2, first1, last1, dest); return; } std::sort(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return std::binary_search(first1, last1, FWD(value)); }); }
في مثالنا مع وظائف لامدا والتقاط المتغيرات ، عادة ما تكون المجموعة التي سنقوم بفرزها هي مجموعة المتغيرات المستخدمة في رمز وظيفة لامدا ، حيث من المحتمل أن تكون هناك متغيرات أقل من المتغيرات في نطاق لامدا المحيطة.
التجزئة
وسيكون الخيار الأخير الذي تمت مناقشته في هذه المقالة هو استخدام التجزئة لمجموعة أصغر بدلاً من فرزها. سيعطينا هذا الفرصة للبحث عن O (1) فيه ، على الرغم من أن بناء التجزئة ، بالطبع ، سيستغرق بعض الوقت (من O (n) إلى O (n * n) ، والذي يمكن أن يصبح مشكلة):
template <typename InputIt1, typename InputIt2, typename OutputIt> void unordered_intersection_3(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_3(first2, last2, first1, last1, dest); return; } std::unordered_set<int> test_set(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return test_set.count(FWD(value)); }); }
سيكون أسلوب التجزئة فائزًا مطلقًا عندما تكون مهمتنا هي مقارنة مجموعة صغيرة A باستمرار مع مجموعة أخرى (كبيرة) من مجموعات B₁ و B₂ و B .... في هذه الحالة ، نحتاج إلى إنشاء تجزئة لـ A مرة واحدة فقط ، ويمكننا استخدام البحث الفوري لمقارنته بعناصر جميع المجموعات B قيد النظر.
اختبار الأداء
من المفيد دائمًا تأكيد النظرية من خلال الممارسة (خاصة في حالات مثل هذه الأخيرة ، عندما يكون من غير الواضح ما إذا كانت التكاليف الأولية للتجزئة ستؤتي ثمارها مع مكاسب في أداء البحث).
في اختباراتي ، أظهر الخيار الأول (مع فرز المجموعتين) دائمًا أسوأ النتائج. عمل فرز مجموعة واحدة صغيرة فقط بشكل أفضل قليلاً على مجموعات بنفس الحجم ، ولكن ليس كثيرًا. لكن الخوارزميات الثانية والثالثة أظهرت زيادة كبيرة جدًا في الإنتاجية (حوالي 6 مرات) في الحالات التي كانت فيها إحدى المجموعات أكبر 1000 مرة من الأخرى.