نواصل دورتنا حول جهاز Monero blockchain ، وستخصص مقالة اليوم لبروتوكول RingCT (المعاملات السرية Ring) ، والذي يقدم المعاملات السرية وتوقيعات الرنين الجديدة. لسوء الحظ ، هناك القليل من المعلومات على الإنترنت حول كيفية عملها ، وحاولنا سد هذه الفجوة.

سنتحدث عن كيف تخفي الشبكة مقدار عمليات النقل باستخدام هذا البروتوكول ، ولماذا رفضنا تواقيع الرنين الكلاسيكية للكريبتوت وكيف ستطور هذه التكنولوجيا بشكل أكبر.
نظرًا لأن هذا البروتوكول هو أحد أكثر التقنيات تعقيدًا في Monero ، سيحتاج القارئ إلى معرفة أساسية حول جهاز سلسلة الكتل هذه والمعرفة السطحية في التشفير على المنحنيات الإهليلجية (لتحديث هذه المعرفة ، يمكنك قراءة الفصول الأولى من مقالنا السابق حول
التوقيعات المتعددة ).
بروتوكول RingCT
واحدة من الهجمات المحتملة على عملات الكريبتونوت هي تحليل blockchain بناءً على معرفة مقدار ووقت المعاملة المرسلة. يسمح
تضييق البحث بشكل كبير عن المخرجات التي تهم المهاجم. للحماية من مثل هذا التحليل ، قدم Monero بروتوكول معاملة مجهول يخفي تمامًا مقدار التحويلات على الشبكة.
الجدير بالذكر أن فكرة إخفاء المبالغ ليست جديدة. كان جريج ماكسويل ، مطور Bitcoin Core ، من أول من وصفها في مقاله
للمعاملات السرية . التطبيق الحالي لـ RingCT هو تعديله مع إمكانية استخدام توقيعات الحلقة (بدونها) ، وبالتالي حصل على اسمها - Ring Confactions.
من بين أمور أخرى ، يساعد البروتوكول على التخلص من مشاكل خلط مخرجات الغبار - مخرجات لكمية صغيرة (يتم الحصول عليها عادة في شكل تغيير من المعاملات) ، مما خلق مشاكل أكثر من تكلفتها نفسها.
في يناير 2017 ، تم عقد شبكة Monero الصلبة ، مما يسمح بالاستخدام الاختياري للمعاملات السرية. وفي سبتمبر من ذلك العام ، مع الإصدار الصعب 6 ، أصبحت مثل هذه المعاملات هي الوحيدة المسموح بها على الشبكة.
يستخدم RingCT عدة آليات في وقت واحد: تواقيع المجموعة المجهولة العفوية القابلة للربط متعددة الطبقات (يشار إليها فيما يلي باسم MLSAG) ، والتزامات Pedersen ، وبروفات النطاق (هذا المصطلح ليس له ترجمة ثابتة إلى اللغة الروسية).
يقدم بروتوكول RingCT نوعين من المعاملات المجهولة: بسيطة وكاملة. يتم إنشاء المحفظة الأولى عندما تستخدم المعاملة أكثر من إدخال ، والثانية - في الحالة المعاكسة. وهي تختلف في التحقق من صحة مبالغ المعاملات والبيانات الموقعة بتوقيع MLSAG (سنتحدث أكثر عن هذا أدناه). علاوة على ذلك ، يمكن إنشاء معاملات من النوع الكامل بأي عدد من المدخلات ، ولا يوجد فرق جوهري. يقول كتاب
"Zero to Monero" حول هذا الموضوع أن قرار حصر المعاملات الكاملة بإدخال واحد تم على عجل وقد يتغير في المستقبل.
توقيع MLSAG
تذكر ما هي المدخلات الموقعة للمعاملة. كل معاملة تنفق بعض المال وتولد. يتم إنشاء الأموال عن طريق إنشاء مخرجات المعاملات (القياس المباشر هو الأوراق النقدية) ، ويصبح الناتج الذي تنفقه المعاملة (بعد كل شيء ، في الواقع الذي ننفق فيه الأوراق النقدية) مدخلاً (بعناية ، من السهل جدًا الخلط هنا).
يشير المدخل إلى العديد من المخارج ، لكنه ينفق واحدًا فقط ، وبالتالي خلق "شاشة دخان" لجعل من الصعب تحليل تاريخ الترجمات. إذا كانت المعاملة تحتوي على أكثر من إدخال واحد ، فيمكن تمثيل هذا الهيكل في شكل مصفوفة ، حيث تكون الصفوف هي المدخلات والأعمدة هي مخرجات العجن. لتثبت للشبكة أن المعاملة تنفق مخرجاتها (تعرف مفاتيحها السرية) ، يتم توقيع المدخلات بتوقيع حلقة. مثل هذا التوقيع يعطي ضمانة بأن الموقّع يعرف المفاتيح السرية من جميع عناصر أي من الأعمدة.
لم تعد المعاملات السرية تستخدم توقيعات حلقة
الكريبتونوت الكلاسيكية ، فقد تم استبدالها بـ MLSAG ، وهي نسخة متعددة المدخلات من تواقيع الحلقة أحادية الطبقة
المماثلة ،
LSAG .
يطلق عليها اسم متعدد الطبقات لأنها توقع عدة مدخلات في وقت واحد ، كل منها مختلط مع عدة أخرى ، أي أن المصفوفة موقعة ، وليس صف واحد. كما سنرى لاحقًا ، يساعد هذا على توفير حجم التوقيع.
دعونا نلقي نظرة على كيفية تكوين توقيع الخاتم ، باستخدام مثال المعاملة التي تنفق 2 مخرجات حقيقية وتستخدم م - 1 عشوائية من blockchain للعجن. تشير إلى المفاتيح العامة للمخرجات التي ننفقها
والصور الرئيسية لهم على التوالي:
وبالتالي ، نحصل على مصفوفة
2 × م . أولاً ، نحتاج إلى حساب ما يسمى بالتحديات لكل زوج من المخرجات:
نبدأ الحسابات بالمخرجات التي ننفقها باستخدام مفاتيحهم العامة:
وأرقام عشوائية
نتيجة لذلك ، نحصل على القيم:
التي نستخدمها لحساب التحدي
الزوج التالي من المخرجات (لتسهيل فهم المكان الذي نستبدل فيه ، قمنا بتمييز هذه القيم بألوان مختلفة). يتم حساب جميع القيم التالية في دائرة وفقًا للصيغ الواردة في الرسم التوضيحي الأول. يتم احتساب التحدي لزوج من المخرجات الحقيقية في النهاية.
كما نرى ، في جميع الأعمدة ، باستثناء العمود الذي يحتوي على المخرجات الحقيقية ، يتم استخدام الأرقام التي تم إنشاؤها بشكل عشوائي
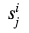
. بالنسبة للعمود، ، نحتاجهم أيضًا. تحويل
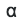
في s:
التوقيع نفسه هو مجموعة من كل هذه القيم:
علاوة على ذلك ، يتم كتابة هذه البيانات في المعاملة.
كما نرى ، يحتوي MLSAG على تحدي واحد فقط
c 0 ، مما يوفر على حجم التوقيع (الذي يتطلب بالفعل مساحة كبيرة). علاوة على ذلك ، أي أداة تحقق تستخدم البيانات
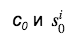
، يستعيد القيم c
1 ، ... ، c
m ويتحقق من ذلك

. وهكذا ، تم إغلاق خاتمنا وتمرير التوقيع.
بالنسبة لمعاملات RingCT من النوع الكامل ، تتم إضافة سطر آخر إلى المصفوفة بمخرجات مختلطة ، ولكننا سنتحدث عن هذا أدناه.
التزامات بيدرسن
يتم استخدام
مخططات الالتزام (غالبًا ما تستخدم المصطلح الإنجليزي - الالتزامات) حتى يتمكن أحد الأطراف من إثبات أنه يعرف سرًا معينًا (رقم) ، دون الكشف عنه فعليًا. على سبيل المثال ، تقوم برمي عدد معين على العظام ، وتفكر في الالتزام وتمريره إلى الطرف المعول. وبالتالي ، في وقت الكشف عن الرقم السري ، ينظر المفتش بشكل مستقل في الالتزام ، وبالتالي التأكد من أنك لم تخدعه.
تُستخدم التزامات Monero لإخفاء مقدار التحويلات واستخدام الخيار الأكثر شيوعًا - التزامات Pedersen. بالمناسبة ، حقيقة غريبة - في البداية ، اقترح المطورون إخفاء المبالغ بالعجن المعتاد ، أي إضافة المخرجات إلى المبالغ التعسفية لإثبات عدم اليقين ، ولكن بعد ذلك تحولوا إلى الالتزامات (ليست حقيقة أنهم قد وفروا على حجم المعاملة ، كما سنرى أدناه).
بشكل عام ، الالتزام كما يلي:
حيث
C هي قيمة الالتزام نفسه ، و
a هي الكمية التي يجب إخفاؤها ، و
H هي النقطة الثابتة على المنحنى البيضاوي (المولد الإضافي) ، و
x هو بعض القناع التعسفي الذي يخفي العامل الذي يتم إنشاؤه عشوائيًا. القناع مطلوب هنا حتى لا يتمكن الطرف الثالث من تحديد قيمة الالتزام بقوة غاشمة بسيطة.
عند إنشاء مخرج جديد ، تحسب المحفظة التزامًا بها ، وعند إنفاقها ، فإنها تأخذ إما القيمة المحسوبة أثناء الإنشاء أو تعيد حسابها مرة أخرى ، اعتمادًا على نوع المعاملة.
Ringct بسيطة
في حالة معاملات RingCT البسيطة ، من أجل التأكد من أن المعاملة خلقت مخرجات مساوية لمجموع المدخلات (لم تجني المال من الجو) ، يجب أن تكون الالتزامات من الأول والثاني هي نفسها ، أي:
تعتبر لجان الالتزام مختلفة قليلاً - بدون قناع:
، حيث يكون مقدار العمولة ، فإنه متاح للجمهور.
يتيح لنا هذا النهج أن نثبت للطرف المعول أننا نستخدم نفس المبالغ دون الكشف عنها.
لتوضيح الأمور ، لنلق نظرة على مثال. افترض أن المعاملة تنفق ناتجين (أي أنها تصبح مدخلات) على 10 و 5 XMRs وتولد ثلاثة مخرجات يبلغ مجموعها 12 XMRs: 3 و 4 و 5 XMRs. في نفس الوقت يدفع عمولة من 3 XMR. وبالتالي ، فإن المبلغ الذي تم إنفاقه بالإضافة إلى المبلغ المولد والعمولة يساوي 15 XMR. دعونا نحاول حساب الالتزامات ونلقي نظرة على الفرق في مبالغها (تذكر الرياضيات):
هنا نرى أن المعادلة تتقارب - مجموع أقنعة المدخلات والمخرجات التي نحتاجها هي نفسها. للقيام بذلك ، تولد المحفظة بشكل عشوائي
x 1 و y 1 و y 2 و y 3 ، وتحسب القيمة المتبقية
x 2 بهذه الطريقة:
باستخدام هذه الأقنعة ، يمكننا أن نثبت لأي شخص يتحقق من أننا لا ننتج أموالًا أكثر مما ننفقه دون الكشف عن المبلغ. الأصل ، أليس كذلك؟
RingCT الكامل
في معاملات RingCT الكاملة ، يكون التحقق من مقدار التحويلات أكثر تعقيدًا إلى حد ما. في هذه المعاملات ، لا تحسب المحفظة التزامات الإدخالات ، ولكنها تستخدم الالتزامات المحسوبة عند إنشائها. في هذه الحالة ، يجب أن نفترض أن الفرق في المبالغ التي لم تعد نحصل عليها تساوي الصفر ، ولكن بدلاً من ذلك:
هنا
z هو الفرق بين أقنعة المدخلات والمخرجات. إذا اعتبرنا
zG مفتاحًا عامًا (وهو في الواقع) ، فإن
z هو مفتاح خاص. وهكذا ، نعرف المفاتيح العامة والمفاتيح الخاصة المقابلة. بعد الحصول على هذه البيانات ، يمكننا استخدامها في توقيع حلقة MLSAG جنبًا إلى جنب مع المفاتيح العامة لمخرجات العجن:
وبالتالي ، سيضمن توقيع الحلقة الصحيح أننا نعرف جميع المفاتيح الخاصة لأحد الأعمدة ، ولا يمكننا معرفة المفتاح الخاص إلا في الصف الأخير إذا لم تنتج المعاملة أموالًا أكثر مما تنفقه. بالمناسبة ، إليك الإجابة على السؤال "لماذا لا يؤدي الفرق في مبالغ الالتزامات إلى صفر" - إذا كانت
zG = 0 ، فسوف نفتح العمود بمخرجات حقيقية.
ولكن كيف يعرف المتلقي مقدار الأموال التي أرسلها إليه؟ كل شيء بسيط هنا - مرسل المعاملة ومفاتيح تبادل المستلمين باستخدام بروتوكول Diffie-Hellman ، باستخدام مفتاح المعاملة ومفتاح العرض الخاص بالمستلم ، وحساب السر المشترك. يكتب المرسل في الحقول الخاصة لبيانات المعاملة على مجموع المخرجات المشفرة باستخدام هذا المفتاح المشترك.
البراهين المدى
ولكن ماذا يحدث إذا استخدمت رقمًا سلبيًا كمبلغ في الالتزامات؟ هذا يمكن أن يؤدي إلى توليد عملات معدنية إضافية! مثل هذه النتيجة غير مقبولة ، لذلك ، نحتاج إلى ضمان أن المبالغ التي نستخدمها ليست سلبية (دون الكشف عن هذه المبالغ ، بالطبع ، وإلا سيكون هناك الكثير من العمل وكلها عبثا). وبعبارة أخرى ، يجب أن نثبت أن المجموع في الفاصل الزمني
[0 ، 2 ن - 1] .
لهذا ، يتم تقسيم مجموع كل ناتج إلى أرقام ثنائية ويتم النظر في الالتزام لكل رقم على حدة. كيف يحدث ذلك ، من الأفضل أن تفكر في مثال.
افترض أن لدينا كميات صغيرة وتناسب 4 بت (في الواقع ، هذه 64 بت) ، وأنشأنا مخرجات بمبلغ 5 XMR. نعتبر الالتزامات لكل فئة والالتزام العام لكامل المبلغ:
علاوة على ذلك ، يتم خلط كل التزام مع بديل
(C i -2 i H) ويتم توقيعه في أزواج من خلال توقيع خاتم Borromeo (توقيع حلقة آخر) الذي اقترحه جريج ماكسويل في عام 2015 (يمكن العثور على المزيد حوله
هنا ):
يُسمى هذا معًا إثبات النطاق ويضمن أن الالتزامات تستخدم مبالغ في الفاصل الزمني
[0، 2 n - 1] .
ما هي الخطوة التالية؟
في التطبيق الحالي ، تأخذ بروفات النطاق مساحة كبيرة - 6176 بايت لكل ناتج. وهذا يؤدي إلى معاملات كبيرة ، وبالتالي عمولات أعلى. لتقليل حجم معاملات Monero ، يقوم المطورون بتقديم بدلاً من Borromeo توقيعات الرصاص - آلية إثبات المدى بدون التزامات أحادية.
وفقًا لبعض التقديرات ، يمكنهم تقليل حجم دليل النطاق إلى 94٪. بالمناسبة ، في منتصف يوليو ، تم
تدقيق التكنولوجيا من قبل Kudelski Security ، والتي لم تكشف عن أي أوجه قصور كبيرة في التكنولوجيا نفسها أو في تنفيذها. يتم استخدام التكنولوجيا بالفعل في شبكة الاختبار ، ومع الشوكة الصلبة الجديدة ، يمكنها على الأرجح الانتقال إلى الشبكة الرئيسية.
اطرح أسئلتك ، واقترح مواضيع لمقالات جديدة حول تقنيات العملة المشفرة ، واشترك في مجموعتنا على
Facebook لمواكبة أحداثنا ومنشوراتنا.