ما هي فكرة الفرز عن طريق الاختيار؟

1. في صفيف فرعي غير مصنفة ، يتم البحث عن الحد الأقصى المحلي (الحد الأدنى).
2. يغير الحد الأقصى (الحد الأدنى) الموجود الأماكن مع العنصر (الأول) الأخير في المصفوفة الفرعية.
3. إذا بقيت المصفوفات الفرعية غير المصنفة في المصفوفة ، انظر النقطة 1.

انحدار غنائي طفيف. في البداية ، في سلسلة مقالاتي ، خططت لتقديم مادة باستمرار حول تصنيف الفئات بترتيب صارم. بعد فرز المكتبة ، تم التخطيط لمقالات حول خوارزميات الإدراج الأخرى: الفرز سوليتير ، الفرز حسب جدول صغير ، الفرز حسب الانقلاب ، إلخ.

ومع ذلك ، فإن الاتجاه الآن هو اللاخطية ، وبالتالي ، دون كتابة جميع المنشورات حول الفرز حسب الإدخالات ، سأبدأ اليوم فرعًا موازًا حول الفرز حسب الاختيار. ثم سأفعل نفس الشيء لفئات خوارزمية أخرى: دمج الأنواع ، أنواع التوزيع ، إلخ. سيسمح ذلك بشكل عام بكتابة المنشورات حول موضوع واحد ، ثم على موضوع آخر. مع مثل هذا التناوب المواضيعي سيكون أكثر متعة.

فرز التحديد

بسيطة وبسيطة - نذهب عبر الصفيف بحثًا عن العنصر الأقصى. يتم تبادل الحد الأقصى الموجود مع العنصر الأخير. انخفض الجزء غير المصنف من الصفيف بعنصر واحد (لا يتضمن العنصر الأخير حيث أعدنا ترتيب الحد الأقصى الموجود). نطبق نفس الإجراءات على هذا الجزء غير المصنف - نجد الحد الأقصى ونضعه في المركز الأخير في الجزء غير المصنف من الصفيف. وهكذا نستمر حتى يتم اختزال الجزء غير المصنف من الصفيف إلى عنصر واحد.

def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return data 

الفرز باختيار بسيط هو بحث مزدوج تقريبي. هل يمكن تحسينها؟ دعونا نلقي نظرة على بعض التعديلات.

فرز مزدوج الاختيار :: فرز مزدوج التحديد

يتم استخدام فكرة مماثلة في فرز شاكر ، وهو نوع من فرز الفقاعة. بالمرور بالجزء غير المصنف من المصفوفة ، بالإضافة إلى الحد الأقصى ، نجد أيضًا الحد الأدنى في نفس الوقت. نضع الحد الأدنى في المقام الأول ، والحد الأقصى في الأخير. وبالتالي ، يتم تقليل الجزء غير المصنف في كل تكرار بعنصرين في وقت واحد.

للوهلة الأولى ، يبدو أن هذا يؤدي إلى تسريع الخوارزمية مرتين - بعد كل تمريرة ، يتم تقليل الصفيف غير المصنف ليس من واحد ، ولكن من جانبين في وقت واحد. ولكن في الوقت نفسه ، زاد عدد المقارنات مرتين ، وظل عدد المقايضات دون تغيير. يؤدي الاختيار المزدوج إلى زيادة سرعة الخوارزمية قليلاً ، وفي بعض اللغات يعمل بشكل أبطأ لسبب ما.

الفرق بين الفرز بالاختيار من فرز الإدراج

قد يبدو أن الفرز عن طريق الاختيار والفرز حسب الإدخالات هو نفس الشيء ، وهو فئة مشتركة من الخوارزميات. حسنًا ، أو الفرز حسب الإدخالات هو نوع من الفرز حسب الاختيار. أو الفرز بالاختيار هو حالة خاصة للفرز حسب الإدخالات. وهناك وهناك ، نتناوب من الجزء غير المصنف من الصفيف لاستخراج العناصر وإعادة توجيهها إلى المنطقة المصنفة.

الاختلاف الرئيسي: في الفرز حسب المدخلات ، نقوم باستخراج أي عنصر من الجزء غير المصنف من الصفيف وإدراجه في مكانه في الجزء المصنف. في فرز الفرز ، نبحث عن قصد عن العنصر الأقصى (أو الحد الأدنى) الذي نكمل به الجزء المصنف من المصفوفة. في الإدخالات ، نبحث عن مكان إدراج العنصر التالي ، وفي الاختيار - نحن نعلم مسبقًا مسبقًا المكان الذي سنضعه ، ولكن في نفس الوقت نحتاج إلى العثور على العنصر الذي يتوافق مع هذا المكان.

وهذا يجعل كلا فئتي الخوارزميات مختلفين تمامًا عن بعضهما البعض في جوهرهما والطرق المستخدمة.

نوع البنغو :: نوع البنغو

ميزة مثيرة للاهتمام في فرز الخيارات هي سرعة الاستقلال لطبيعة البيانات التي يتم فرزها.

على سبيل المثال ، إذا تم تقريب المصفوفة تقريبًا ، فعندئذ كما تعلم ، فإن الفرز حسب الإدخالات سيعالجها بشكل أسرع (حتى أسرع من الفرز السريع). المصفوفة ذات الترتيب العكسي للفرز حسب الإدخالات هي حالة متدهورة ، وسوف تقوم بفرزها لأطول فترة ممكنة.

وللفرز عن طريق التحديد ، لا يلعب الترتيب الجزئي أو العكسي للصفيف دورًا - سيعالجه بنفس سرعة عشوائي عشوائي. أيضًا ، بالنسبة للفرز الكلاسيكي ، لا يهم إذا كان المصفوفة تتكون من عناصر فريدة أو متكررة - وهذا لا يؤثر عمليًا على السرعة.

ولكن من حيث المبدأ ، يمكنك إنشاء وتعديل الخوارزمية بحيث تعمل بشكل أسرع مع بعض مجموعات البيانات. على سبيل المثال ، يأخذ فرز البنغو في الاعتبار إذا كان المصفوفة تتكون من عناصر مكررة.



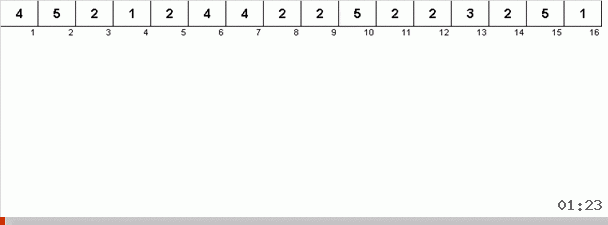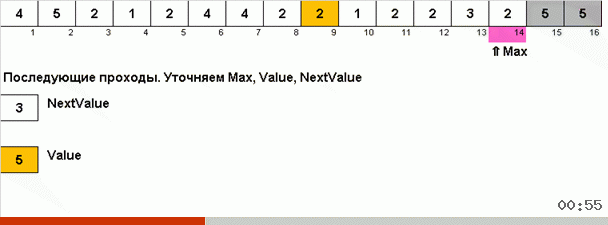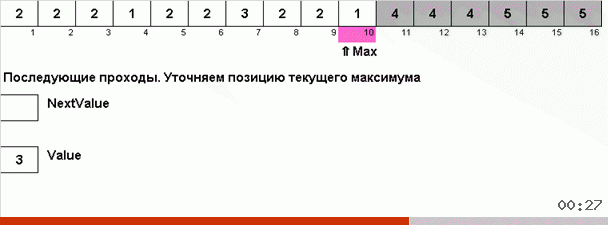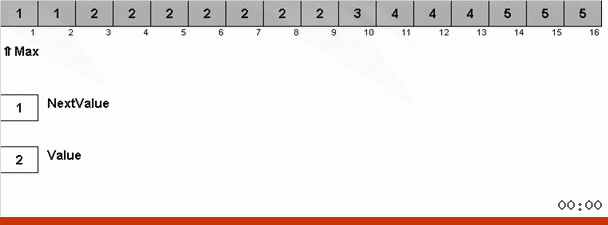
الحيلة هنا هي أنه لا يتم تذكر الحد الأقصى للعنصر فقط في الجزء غير المنتظم ، ولكن يتم أيضًا تحديد الحد الأقصى للتكرار التالي. هذا يسمح بتكرار الحد الأقصى ليس للبحث عنها مرة أخرى في كل مرة ، ولكن لوضعها في مكانها بمجرد مواجهة هذا الحد الأقصى مرة أخرى في الصفيف.

التعقيد الخوارزمي بقي على حاله. ولكن إذا كان المصفوفة تتكون من أرقام متكررة ، فإن الفرز البنغو سيتعامل أسرع بعشر مرات من الفرز العادي حسب الاختيار.

 # - def bingo(data): #  . max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 #  . while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return data 

دورة الفرز :: فرز الدورة

يعد فرز الحلقة أمرًا مثيرًا للاهتمام (وقيمًا من وجهة نظر عملية) في أن التغييرات بين عناصر الصفيف تحدث إذا وفقط إذا تم وضع العنصر في مكانه النهائي. يمكن أن يكون هذا مفيدًا إذا كانت إعادة الكتابة في مصفوفة مكلفة للغاية وتتطلب رعاية الذاكرة الفعلية تقليل عدد التغييرات على عناصر الصفيف.



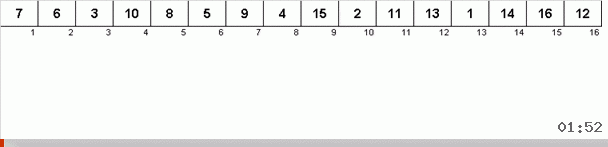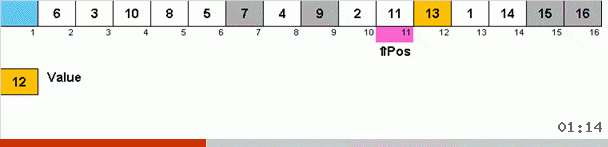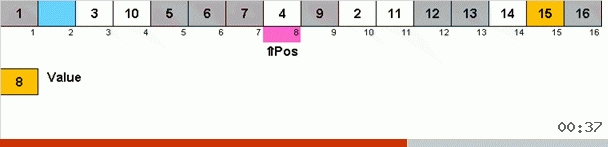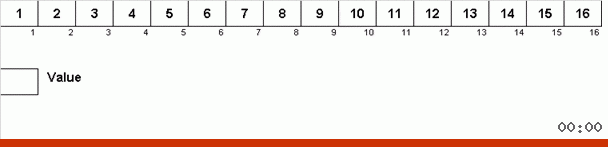
يعمل مثل هذا. نقوم بالفرز عبر المصفوفة ، استدعاء X الخلية التالية في هذه الحلقة الخارجية. ونلقي نظرة على المكان في الصفيف الذي نحتاجه لإدراج العنصر التالي من هذه الخلية. في المكان الذي تريد لصق عنصر آخر فيه ، نرسله إلى الحافظة. بالنسبة لهذا العنصر في المخزن المؤقت ، نبحث أيضًا عن مكانه في الصفيف (والصقه في هذا المكان ، ونرسل إلى المخزن المؤقت العنصر الذي يظهر في هذا المكان). وبالنسبة للرقم الجديد في المخزن المؤقت ، نقوم بنفس الإجراءات. إلى متى يجب أن تستمر هذه العملية؟ حتى يتضح أن العنصر التالي في الحافظة هو العنصر الذي يجب إدراجه بدقة في الخلية X (المكان الحالي في الصفيف في الحلقة الرئيسية للخوارزمية). عاجلاً أم آجلاً ستحدث هذه اللحظة ، ثم في الحلقة الخارجية يمكنك الذهاب إلى الخلية التالية وتكرار نفس الإجراء لها.

في أنواع أخرى ، بالاختيار ، نبحث عن الحد الأقصى / الأدنى لوضعهم في المركز الأخير / الأول. في ترتيب الفرز ، يتبين أنه يقع على الأقل المكان الأول في المجموعة الفرعية ، كما كان ، في عملية كيفية وضع العديد من العناصر الأخرى في أماكنها الصحيحة في مكان ما في منتصف المصفوفة.

وهنا ، يبقى التعقيد الخوارزمي أيضًا داخل O ( n ² ). من الناحية العملية ، يعمل التصنيف الدوري حتى أبطأ عدة مرات من الفرز العادي عن طريق الاختيار ، حيث يتعين عليك الركض حول الصفيف أكثر والمقارنة أكثر. هذا هو ثمن أقل عدد ممكن من عمليات إعادة الكتابة.

 #   def cycle(data): #        for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      ,   #      if pos == cycleStart: continue #   ,     #        while value == data[pos]: pos += 1 data[pos], value = value, data[pos] #      , #         while pos != cycleStart: # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      #      while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return data 

فرز فطيرة

خوارزمية أتقنت جميع مستويات الحياة - من البكتيريا إلى بيل جيتس .



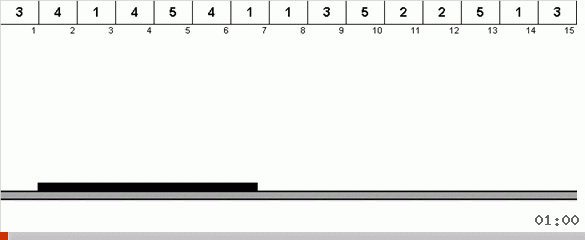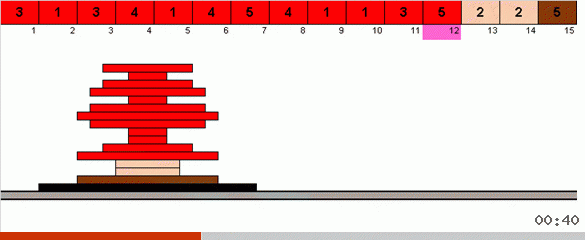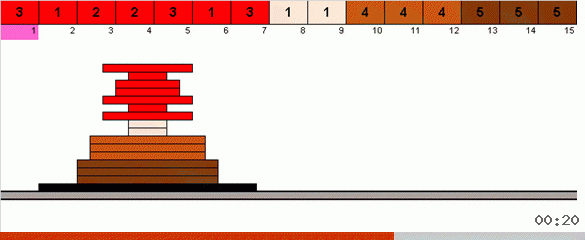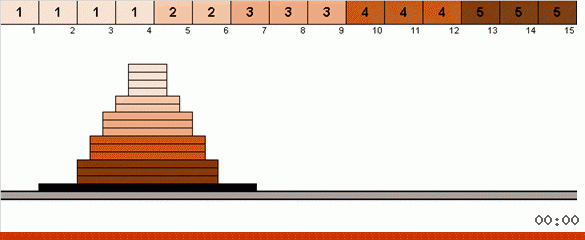
في أبسط الحالات ، نحن نبحث عن العنصر الأقصى في الجزء غير المصنف من الصفيف. عندما يتم العثور على الحد الأقصى ، نقوم بدوران حادان. أولاً ، ندير سلسلة العناصر بحيث يكون الحد الأقصى في الطرف المقابل. ثم نقوم بقلب المجموعة الفرعية غير المصنفة بالكامل ، ونتيجة لذلك يقع الحد الأقصى في مكانه.

تؤدي هذه الكورديليت ، بشكل عام ، إلى تعقيد خوارزمي في O ( n ³ ). تتداعى هذه الأهداب المدربة في ضربة واحدة (لذلك ، في تنفيذها ، يكون التعقيد O ( n ² )) ، وعند البرمجة ، يكون عكس جزء من الصفيف دورة إضافية.

يعد تصنيف الفطيرة أمرًا مثيرًا للاهتمام للغاية من وجهة نظر رياضية (كانت أفضل العقول تفكر في تقييم الحد الأدنى لعدد التقلبات الكافية للفرز) ، وهناك صيغ أكثر تعقيدًا للمشكلة (مع حرق ما يسمى جانب واحد). إن موضوع الفطائر مثير للغاية ، ربما سأكتب دراسة أكثر شمولاً حول هذه القضايا.

 #   def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): #      maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: #    ,    if maxindex != 0: #  , #     data[:maxindex+1] = reversed(data[:maxindex+1]) #    , #      data[:size] = reversed(data[:size]) return data 

---

يعتبر فرز التحديد فعالاً مثل تنظيم البحث عن الحد الأدنى / الحد الأقصى للعنصر في الجزء غير المصنف من الصفيف. في جميع الخوارزميات التي تم تحليلها اليوم ، يتم البحث في شكل بحث مزدوج. وفي البحث المزدوج ، بغض النظر عما قد يقوله المرء ، لن يكون التعقيد الخوارزمي دائمًا أفضل من O ( n ² ). هل يعني هذا أن جميع الفرز بالاختيار محكوم عليها بمعنى تعقيد مربع؟ على الإطلاق ، إذا تم تنظيم عملية البحث بطريقة مختلفة تمامًا. على سبيل المثال ، ضع في اعتبارك مجموعة بيانات على أنها كومة بحث وابحث عنها. ومع ذلك ، فإن موضوع الأكوام ليس مقالًا ، بل ملحمة كاملة ، سنتحدث بالتأكيد عن الأكوام ، ولكن مرة أخرى.

المراجع

الاختيار / الدورة ، الفطيرة / الفطائر

مقالات سلسلة:

• تطبيق Excel AlgoLab.xlsm
• أنواع التبادل
• أنواع الإدراج
• فرز حسب التحديد
  • الفرز والتعديلات في كومة الذاكرة المؤقتة
  • تصنيف كومة ذات الحدين وضعف
  • فرز البطولة
  • تصنيف شجرة الديكارتي
  • نوع الغابة
  • مقارنة الأنواع بالاختيار
• دمج الأنواع
• فرز حسب التوزيع
• الفرز الهجين

تمت إضافة لعبة البنغو والدورة والفطيرة اليوم إلى تطبيق AlgoLab. في الأخير ، فيما يتعلق برسم الفطائر ، تم وضع قيود - يجب أن تكون قيم العناصر في الصفيف من 1 إلى 5. يمكنك بالطبع وضع المزيد ، ولكن وحدات الماكرو ستأخذ عشوائيًا أرقامًا من هذا النطاق.