👿 👧🏻 🔔 تطوير محول فيديو من 264 إلى avi ل Dashcam QCM-08DL 🚉 👩🏿‍🤝‍👩🏻 🌉

في الواقع ، تم تخصيص المقالة لتطوير برنامج لإعادة حزم فيديو DVR من حاوية إلى أخرى ، إذا كان يمكن أن يطلق عليه التحويل. على الرغم من كل حياتي ، اعتقدت أن المحول يشارك في تحويل (تحويل) تنسيق الفيديو. هذه المقالة هي الجزء الثاني من مطبوعتي الأخيرة ، حيث تحدثت بالتفصيل حول الوصول إلى جميع تسجيلات الفيديو من DVR. ولكن في بداية المنشور ، قمت بتعيين مهمة أخرى: دراسة الخوارزمية التي يعمل من خلالها برنامج إعادة التعبئة 264-avi القياسي وإنشاء نفس البرنامج الذي يؤدي نفس العمليات ، ولكن ليس على واحدة ، ولكن على مجموعة كاملة من الملفات ، علاوة على ذلك "نقرة واحدة".

سأشرح مرة أخرى جوهر كل شيء بلغة بسيطة.

لدى المستخدم مسجل فيديو ، على سبيل المثال ، النموذج الشعبي QCM-08DL. يحتاج إلى فيديو لتاريخ ووقت محددين. يمكنه إزالته إما على محرك أقراص USB محمول أو من خلال واجهة على الويب من DVR إلى جهاز كمبيوتر. سيتم فتح ملف الفيديو المستخرج (الامتداد .264) فقط في برنامج المشغل الذي يأتي مع DVR. اللاعب غير مريح للغاية. لا يزال بإمكانك فتحه في مشغل VLC عن طريق تعيين وضع RAW H264 في إعدادات إزالة تعدد الإرسال (إعدادات للمستخدمين المتقدمين). ولكن في نفس الوقت ، على ما يبدو ، فإن كتل تدفقات الصوت ، التي يتم تفسيرها على أنها فيديو ، ولا يوجد صوت ، تتداخل مع التشغيل العادي. ولفتح الفيديو في أي مشغل ، يجب أولاً تحويل ملف .264 إلى بعض التنسيقات الشائعة ، على سبيل المثال ، avi. يتم تضمين برنامج تحويل أيضًا مع DVR. لكنها أيضا غير مرتاحة للغاية. عندما يتعلق الأمر بملف واحد أو أكثر ، فلا توجد مشاكل. ومع ذلك ، عندما تكون المهمة هي الوصول إلى جميع مقاطع الفيديو على محرك الأقراص الثابتة ، وأكثر من ذلك لتحويلها جميعًا إلى تنسيق شائع ، فإن الأدوات القياسية غير مناسبة عمليًا.

تم حل مشكلة الوصول إلى جميع الملفات. كان هذا موضوع المنشور الأخير. نشرع في حل المشكلة الثانية. لقد تلقيت بالفعل "نصيحة عملية": يكفي إعادة تسمية الامتداد من "264" إلى "avi" في اسم الملف ، وسيحدث كل شيء بشكل خاطئ ، كما يقولون ، ليس هناك ما يزعجك. لكن هذا هو الخطأ الأكثر شيوعًا لأي مستخدم عادي ، والذي ، كقاعدة عامة ، لا يفهم القضايا ذات الصلة.

في منشور سابق ، كتبت بالفعل بإيجاز عن بنية ملف المصدر .264. دعني أذكرك.

تنشأ المعلومات الرئيسية مع تدفقات الصوت والفيديو عند إزاحة 65.536 بايت. تبدأ كتل تدفق الفيديو برأس من 8 بايت "01dcH264" (وجد أيضًا "00dcH264"). تصف وحدات البايت الأربعة التالية حجم الكتلة الحالية لدفق الفيديو بالبايت. بعد 4 بايت من الأصفار (00 00 00 00) ، تبدأ كتلة دفق الفيديو نفسها. تحتوي كتل التدفق الصوتي على العنوان "03wb" (على الرغم من أنه وفقًا لملاحظاتي ، فإن الحرف الأول من الرأس في بعض الحالات لم يكن بالضرورة "0"). بعد - 12 بايت من المعلومات التي لم أحسبها بعد. بدءًا من 17 بايت - دفق صوتي بطول ثابت 160 بايت. لا توجد علامات في نهاية الملف.

سأعلق على ما سبق. كل ما يصل إلى إزاحة 65.536 بايت تبين أنه غير محلول وغير ضروري. من إزاحة 65.536 بايت إلى الرأس الأول للدفق ، هناك فجوة صغيرة ، لم يتم أيضًا حل محتوياتها ، وعلاوة على ذلك ، كما راجعت ، لا تظهر في ملف avi بعد التحويل بواسطة برنامج عادي.

تمثل كل كتلة من دفق الفيديو إطار واحد. الحرف الأول في رأس كتل دفق الفيديو هو اختياريا "0". لم أتمكن من معرفة غرضه ، لأنه ، كما اكتشفت ، ليس مفتاح حل المهمة. يمكن أن يكون الحرف الثاني لرأس دفق الفيديو إما "1" أو "0". في الحالة الثانية ، يكون محتوى كتلة دفق الفيديو هو ما يسمى بالإطار المرجعي. وفي الحالة الأولى ، يكون محتوى كتلة دفق الفيديو عبارة عن إطار مضغوط مشفر يعتمد على الإطار المرجعي. حجم محتويات الإطار المرجعي أكبر بكثير من حجم محتويات الإطار الفرعي المضغوط. تعتمد فترة تكرار الإطار المرجعي على الأرجح على إعدادات نسبة الضغط في DVR. ولكن في حالتي ، كانت فترة التكرار 1 إطار / ثانية.

أعطى البرنامج العادي لإعادة حزم الفيديو من الحاوية "264" إلى الحاوية "avi" نتائج مختلفة فيما يتعلق بمعدل الإطارات. في حالة مقاطع الفيديو التي تم تسجيلها في وضع الدقة العالية (704 * 576) ، كان معدل الإطارات 20 إطارًا في الثانية. وفي حالة الدقة المنخفضة (352 * 288) - 25 لقطة / ثانية. يتم توفير هذه المعلومات بواسطة الأداة المساعدة MediaInfo. كما توضح أن حجم الفيديو هو نفسه في أي حال: 720 * 576 ، وأن حجم دفق الفيديو (تقارير الأداة المساعدة) هو 704 * 576 أو 352 * 288. يتم نشر معظم اللاعبين خصيصًا لحجم دفق الفيديو. ومع ذلك ، قابلت لاعبًا عرض وضع نصف الشاشة بشكل غير صحيح عند تشغيل ملف 352 * 288. كنت أرغب في إصلاح هذا العيب البسيط في إعادة التعبئة بدوام كامل من خلال النظر في وحدات بايت محتوى دفق الفيديو وسحب معلومات حول حجم الإطار من هناك. ولكن على عجل ، لم أستطع فعل ذلك. ما ورد أعلاه موضح في الشكل أدناه.

الآن عن معدل الإطار. كما اكتشفت ، فإن أداة إعادة التعبئة العادية لا تصل إلى أي حقل رأس للحاوية "264". وهو يحكم على معدل الإطار عن طريق حساب نسبة عدد كتل الفيديو وتدفقات الصوت. ولا يتم تقريب هذه القيمة في الحساب إلى أقرب قيمة كاملة ، كما يمكن رؤيته من الشكل أعلاه (دائري باللون الأخضر). كما اكتشفت ، عدد كتل دفق الصوت لكل وحدة زمنية ثابت دائمًا وفي كل مكان (في أي ملف) ، وهو 25 كتلة في الثانية. إذا قمت بفحص ملف الفيديو بتردد 20 إطارًا / ثانية ، فإن الإطار المرجعي (الكتلة) يحدث كل 19 إطارًا مضغوطًا ، وفي حالة 25 إطارًا / ثانية. - كل 24 إطار مضغوط.

نواصل دراسة هيكل رأس دفق الفيديو. اكتشفنا البايتات الثمانية الأولى: هذا هو ملصق الإطار المرجعي أو المضغوط بالإضافة إلى الكلمة الرئيسية "H264". تصف وحدات البايت الأربعة التالية ، كما اكتشفت ، ليس الحجم الدقيق ، ولكن الحجم التقريبي لمحتويات دفق الفيديو. تقوم أداة إعادة التعبئة المنتظمة بإلقاء كل وحدات البايت من هذا المحتوى بالكامل ، ثم تكتب الحجم الناتج في الحقول المقابلة لحاوية avi. وتختلف هذه القيمة عن القيمة المحددة في الحقل المقابل لملف .264 المصدر.

جزئياً ، خمنت اثني عشر بايت من المعلومات بعد عنوان كتلة دفق الصوت. على أي حال ، العناصر الرئيسية هي 4 بايت الأخيرة ، وبعد ذلك يبدأ دفق الصوت. هذان رقمان من 16 بت تصفان المعلمات الأولية لنظام فك التشفير التكراري من ADPCM إلى PCM. يؤدي فك التشفير إلى زيادة حجم دفق الصوت بمقدار 4 مرات. عند البحث عن الملفات مقدمًا ، اكتشفت أن أداة إعادة التعبئة بدوام كامل تقوم بفك تشفير الصوت ، ولكنها تترك محتويات الفيديو دون تغيير.

بدون معرفة عميقة ، حاولت لفترة طويلة معرفة خوارزمية فك التشفير التي تم استخدامها في حالتي. تخمين حدسي بالفعل أنه تم تطبيق طريقة ضغط ADPCM. بتعبير أدق ، ليس بشكل حدسي ، ولكن مع نهج كفء ، بناءً على حقيقة أن الدفق الصوتي مضغوط 4 مرات بالضبط. وعندما أقوم بفتح جزء في Adobe Audition مثل RAW بتنسيقات مختلفة (ومقارنة نفس الجزء بعد إعادة التعبئة مع برنامج عادي) ، أعطتني ADPCM نتيجة صوتية مشابهة جدًا (ولكن ليست دقيقة). لتحليل خوارزمية الضغط ، ساعدتني المعلومات الموجودة على موقع wiki.multimedia.cx/index.php/IMA_ADPCM . لقد تعرفت هنا على معلمي فك التشفير الأوليين ، ثم باستخدام "طريقة poke" ، أدركت أن هذه المعلمات الأولية تم تسجيلها في 4 بايت قبل بدء الدفق الصوتي. سأصف عملية الخوارزمية وأقدم تفسيرًا رياضيًا تقريبيًا (تحت المفسد).

تفاصيل خوارزمية فك تشفير ADPCM

هناك سلسلة من العينات

x_{0} ، x_{1} ، x_{2} ، ا ل ن ق ا ط .

$x_0 ، x_1 ، x_2 ، \ النقاط.$ بالإضافة إلى ذلك ، كما سبق ذكره ، هناك معلمتان أوليتان

y_{0}

$y_0$ و

s_{0}

$s_0$ . تحتاج إلى الحصول على تسلسل عينة جديد

y_{0} ، y_{1} ، y_{2} ا ل ن ق ا ط .

$y_0 ، y_1 ، y_2 \ النقاط.$ . كما يمكنك بالفعل تخمين ، فإن أول عينة إخراج معروفة بالفعل: تتزامن مع إحدى المعلمات الأولية

y_{0}

$y_0$ . هذا شيء آخر غير "النزوح الأولي". وتجدر الإشارة إلى أن عينات المدخلات (المصدر) مشفرة بأربع بتات. بالنسبة للأنواع الموقعة ، تقع الأعداد الصحيحة من -8 إلى 7 ، شاملة ، تحت التشفير. الشيء الأكثر أهمية ، في الواقع ، هو المسؤول عن علامة الرقم. عينات PCM الإخراج ، التي يتم الحصول عليها بعد فك التشفير ، لها تنسيق قياسي موقع 16 بت.

تحليل رمز الخوارزمية في C ، يمكنك رؤية جدولين. يتم سردها أدناه.

int ima_index_table[] = { -1, -1, -1, -1, 2, 4, 6, 8 };

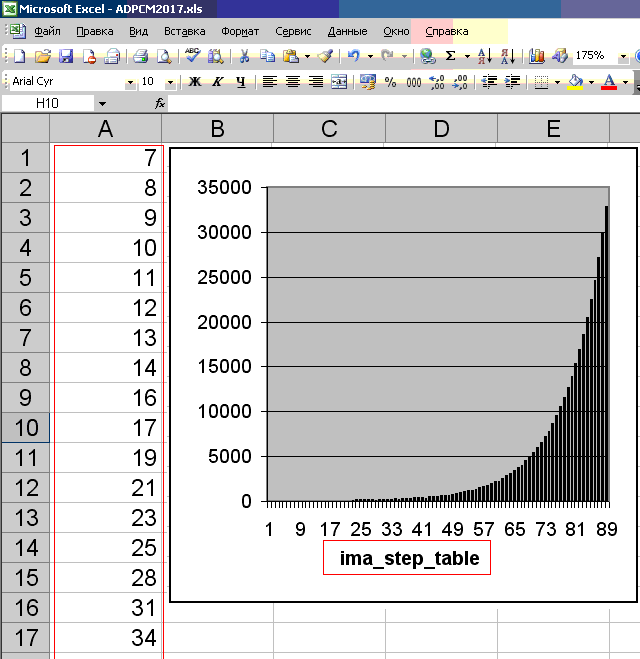
 int ima_step_table[] = { 7, 8, 9, 10, 11, 12, 13, 14, 16, 17, 19, 21, 23, 25, 28, 31, 34, 37, 41, 45, 50, 55, 60, 66, 73, 80, 88, 97, 107, 118, 130, 143, 157, 173, 190, 209, 230, 253, 279, 307, 337, 371, 408, 449, 494, 544, 598, 658, 724, 796, 876, 963, 1060, 1166, 1282, 1411, 1552, 1707, 1878, 2066, 2272, 2499, 2749, 3024, 3327, 3660, 4026, 4428, 4871, 5358, 5894, 6484, 7132, 7845, 8630, 9493, 10442, 11487, 12635, 13899, 15289, 16818, 18500, 20350, 22385, 24623, 27086, 29794, 32767 };

يمكن اعتبار هذين الصفيفين "السحريين" دالات جدولة ، في الحجج التي يتم فيها استبدال نفس المعلمتين الأوليتين. أثناء التكرار ، مع كل خطوة ، يتم إعادة حساب المعلمات واستبدالها في هذه الجداول مرة أخرى. أولاً ، دعنا نرى كيف يتم تنفيذ ذلك في التعليمات البرمجية.

نعلن ما يلزم ، بما في ذلك المتغيرات المساعدة.

 int current1; int step; int stepindex1; int diff; int current; int stepindex; int value; //  ;

قبل بدء التكرار ، تحتاج إلى تعيين المعلمة الأولية للمتغير الحالي

y_{0}

$y_0$ و stepindex المتغير

s_{0}

$s_0$ . يتم ذلك خارج الخوارزمية المعنية ، لذلك لا أعكس هذا مع التعليمات البرمجية. فيما يلي التحولات التي يتم إجراؤها في دائرة (في حلقة).

  value = read(input_sample); //   ; current1 = current; stepindex1 = stepindex; step = ima_step_table[stepindex1]; diff = step>>3; if(value & 1){ diff += step >> 2; } if(value & 2){ diff += step >> 1; } if(value & 4){ diff += step; } if(value & 8){ current1 -= diff; if(current1 < -32768){ //,  ""; current1 = -32768; } }else{ current1 += diff; if(current1 > 32767){ //,  ""; current1 = 32767; } } //      :   current1; stepindex1 += ima_index_table[value & 7]; if(stepindex1 < 0){ // ""; stepindex1 = 0; } if(stepindex1 > 88){ // ""; stepindex1 = 88; } output_sample = curent1; //   ; current = current1; stepindex = stepindex1;

في الخطوة المتغيرة المساعدة من المصفوفة ima_step_table ، تتم كتابة القيمة في الفهرس stepindex1. بالنسبة إلى التكرار الأول ، هذه هي المعلمة الأولية

s_{0}

$s_0$ ، لمزيد من التكرار هذه معلمة معاد حسابها

s_{i}

$s_i$ . ثم يتم تقسيم القيمة من هذا المصفوفة على 8 (على ما يبدو ، بشكل كامل) بعملية تحويل صغيرة إلى اليمين ، ويتم تهيئة المتغير diff نتيجة لهذا التقسيم. بعد ذلك ، يتم تحليل البتات الثلاثة الأقل أهمية لقيمة عينة الإدخال ، ويمكن تعديل المتغير diff بثلاثة مصطلحات وفقًا لحالاتها. المصطلحات هي تقسيم صحيح مشابه لقيمة الفرق ب 4 (>> 2) ، 2 (>> 1) أو فرق بدون تغييرات (فليكن تقسيمًا على 1 للتعميم). ثم يتم تحليل البت الأكثر أهمية (الموقّع) من قيمة عينة الإدخال. بناءً على حالته ، يتم إضافة المتغير diff الذي تم إنشاؤه قبل ذلك أو طرحه إلى المتغير الحالي 1. ستكون هذه قيمة عينة الإخراج. للصحة ، تقتصر القيم على الأعلى والأسفل. ثم يتم ضبط stepindex1 عن طريق إضافة القيمة من الصفيف ima_index_table عن طريق فهرس قيمة عينة الإدخال مع إعادة تعيين بت الإشارة إلى الصفر. تخضع قيم Stepindex1 أيضًا للحد. في النهاية ، قبل تكرار هذه الخوارزمية ، يتم تعيين القيم الحالية وخطوات Stepindex للقيم المعاد حسابها فقط لـ current1 و stepindex1 ، ويتم تكرار الخوارزمية مرة أخرى.

يمكنك محاولة اكتشافها من أجل فهم كيفية تكوين المتغير diff تقريبًا. دع

f_{i} = f (s_{i})

$f_i = f (s_i)$ . هذه هي قيم متغير الخطوة في كل خطوة من ط إلى التكرار ، كقيم دالة (صفيف) الوسيطة

s_{i}

$s_i$ أين

i = 0 ، 1 ، 2 ، d o t s

$i = 0 ، 1 ، 2 ، \ dots$ . للراحة ، نشير إلى المتغير diff على أنه

d

$d$ . بناءً على منطق الاستدلال الموضح أعلاه ، لدينا:

d_{i} = f r a c f_{i} 8 + x_{i}^{(0)} f r a c f_{i} 4 + x_{i}^{(1)} f r a c f_{i} 2 + x_{i}^{(2)} f_{i} ،

$d_i = \ frac {f_i} {8} + x ^ {(0)} _ i \ frac {f_i} {4} + x ^ {(1)} _ i \ frac {f_i} {2} + x ^ {( 2)} _ if_i،$

أين

x_{i}^{(0)} ، x_{i}^{(1)} ، x_{i}^{(2)}

$x_i ^ {(0)} ، x_i ^ {(1)} ، x_i ^ {(2)}$ - 3 بتات منخفضة من الرقم

x_{i}

$x_i$ . مما يؤدي إلى قاسم مشترك ، نحول هذا التعبير إلى شكل أكثر ملاءمة:

d_{i} = f r a c f_{i} 8 B i g g (1 + 2 x_{i}^{(0)} + 4 x_{i}^{(1)} + 8 x_{i}^{(2)} B i g g) =

$d_i = \ frac {f_i} 8 \ Bigg (1 + 2x_i ^ {(0)} + 4x_i ^ {(1)} + 8x_i ^ {(2)} \ Bigg) =$

= f r a c f_{i} 8 B i g g (1 + 2 B i g (x_{i}^{(0)} + 2 x_{i}^{(1)} + 4 x_{i}^{(2)} B i g) B i g g) = f r a c f_{i} 8 (2 x_{i} + 1) .

$= \ frac {f_i} 8 \ Bigg (1 + 2 \ Big (x_i ^ {(0)} + 2x_i ^ {(1)} + 4x_i ^ {(2)} \ Big) \ Bigg) = \ frac { f_i} {8} (2x_i + 1).$

يعتمد التحويل الأخير على حقيقة أنه ، إلى حد ما ، ثلاث بتات على الأقل (0 أو 1) من الرقم

x_{i}

$x_i$ بالمعاملات المعروضة ، هناك شيء آخر غير كتابة القيمة المطلقة لهذا الرقم ، وأهم جزء من الرقم

x_{i}

$x_i$ ستطابق علامة التعبير بالكامل. كذلك وفقًا للصيغة

y_{i + 1} = y_{i} + d_{i}

$y_ {i + 1} = y_i + d_i$

يتم حساب قيمة عينة جديدة بناءً على القديمة. بالإضافة إلى ذلك ، يتم حساب قيمة متغيرة جديدة.

s

$s$ :

s_{i + 1} = s_{i} + t (| x_{i} |) .

$s_ {i + 1} = s_i + t (| x_i |).$

تشير الوحدة في الصيغة إلى أن المتغير

x_{i}

$x_i$ يدخل في العمل

t

$t$ باستثناء بتة الإشارة الأكثر أهمية ، والتي تنعكس في التعليمات البرمجية. وظيفة

t

$t$ هي قيمة المصفوفة ima_index_table مع الفهرس المقابل للوسيطة.

في وصف الصيغ ، أهملت عمليات التقييد أعلاه وأدناه. يبدو المخطط التكراري الكلي شيئًا مثل هذا:

y_{0} ؛ s_{0} ؛ x_{0} ، x_{1} ، x_{2} ، d o t s ؛

$y_0 ؛ \ s_0 ؛ \ \ x_0 ، x_1 ، x_2 ، \ dots \ ؛$

d_{i} = f r a c f (s_{i}) 8 b i g (2 x_{i} + 1 b i g) \؛

$d_i = \ frac {f (s_i)} {8} \ big (2x_i + 1 \ big) \؛$

y_{i + 1} = y_{i} + d_{i} \؛

$y_ {i + 1} = y_i + d_i \؛$

s_{i + 1} = s_{i} + t (| x_{i} |) \؛

$s_ {i + 1} = s_i + t (| x_i |) \؛$

i = 0 ، 1 ، 2 ، d o t s .

$i = 0، 1، 2، \ dots.$

بعمق شديد في نظرية التشفير / فك التشفير ADPCM التي لم أخوض فيها. ومع ذلك ، فإن قيم الجدول للصفيف ima_step_table (المكون من 89 قطعة) ، إذا حكمنا من خلال انعكاسها على الرسم البياني (انظر الشكل أدناه) ، تصف التوزيع الاحتمالي للعينات بالنسبة لخط الصفر. من الناحية العملية ، عادة ما يكون هذا هو الحال: كلما كانت العينة أقرب إلى خط الصفر ، زاد حدوثها. لذلك ، يعتمد ADPCM على نموذج احتمالي ، ولا يمكن بأي حال من الأحوال تحويل أي مجموعة مصادر لعينات PCM 16 بت بشكل صحيح إلى عينات ADPCM 4 بت. بشكل عام ، ADPCM هي PCM مع خطوة تكمية متغيرة. على ما يبدو ، يعكس هذا الرسم البياني هذه الخطوة المتغيرة للغاية. يتم اختياره بشكل صحيح ، بناءً على قانون توزيع البيانات الصوتية في الممارسة.

الآن دعنا ننتقل إلى وصف هيكل حاوية avi. في الواقع ، إنه هيكل هرمي معقد.

ولكن ، بعد تبسيط المهمة لحالة خاصة ، قدمت بنية الطيران في شكل خطي. والنتيجة هي: يتكون ملف avi من رأس كبير ، صفر بايت تخطي (JUNK) ، منطقة تدفقات الصوت والفيديو (مع رؤوسها وأحجام المحتوى) ، وقائمة الفهارس. يعمل الأخير ، على وجه الخصوص ، للتمرير عبر الفيديو في المشغل. بدون هذه القائمة ، لن يعمل التمرير (محدد). إنه فقط جدول محتويات يسرد الأسماء الرئيسية لكتل الدفق (مطابقة الأسماء في رؤوس الكتلة) ، والأحجام المقابلة للمحتوى ، وقيم الإزاحة (العناوين) المتعلقة ببداية منطقة الدفق.

الآن يمكنك المضي قدما في تطوير البرنامج. وصف محدد للمشكلة على النحو التالي.

في جذر القسم X: يوجد دليل "DVR". يحتوي هذا الدليل على العديد من الأدلة الفرعية غير الفارغة (والأدلة الفرعية فقط) بأسماء تتوافق مع تواريخ معينة. يوجد في كل من هذه الدلائل الفرعية العديد من الملفات ذات الأسماء المختلفة والملحق "264". مطلوب في القسم Y: إنشاء دليل "DVR" وفيه نفس الأدلة الفرعية كما في القسم X:. املأ كل من هذه الدلائل الفرعية بملفات تحمل نفس الأسماء المطابقة ، ولكن مع ملحقات لا "264" ، ولكن "avi". يجب الحصول على ملفات avi هذه من ملفات 264 الأصلية عن طريق معالجتها ، والتي تكرر بطريقة أو بأخرى خوارزمية برنامج موجود. تتكون المعالجة من إعادة حزم تدفقات الفيديو مباشرة وإعادة حزمها مع فك تدفقات الصوت وتنسيق ملف avi. يجب تشغيل البرنامج من سطر الأوامر كما يلي: "264toavi.exe X: Y:" ، حيث "264toavi.exe" هو اسم البرنامج ، "X:" هو قسم المصدر ، "Y:" هو قسم الوجهة.

في الواقع ، لتبسيط المهمة ، كان من الممكن كتابة برنامج يتعامل فقط مع تحويل (إعادة حزم) ملف واحد ، مما يجعله يومين: اسم ملف الإدخال واسم ملف الإخراج. وبعد ذلك ، لتنفيذ إعادة تجميع المجموعة فقط ، يمكنك كتابة ملف دفعي للأمر (bat) باستخدام أدوات أخرى ، على سبيل المثال ، Excel. لكنني نفذت برنامجًا كاملاً مرهقًا جدًا. من غير المرجح أن يستحق كود المصدر انتباه القراء. سوف أصف هيكل رمز البرنامج.

البرنامج مكتوب بلغة C في بيئة تطوير Dev-C ++ مع عناصر WinAPI. يطبق البرنامج ثلاث وظائف مساعدة كبيرة: وظيفة توليد رأس AVI الأولي ، ووظيفة فك ترميز عينة صوتية ، ووظيفة مسح الملف المصدر "264" بالكلمات. في الكلمات ، أسمي جزءًا من 4 بايت. وقد لوحظ أن أحجام الرؤوس ومحتويات جميع التدفقات هي مضاعفات أربعة بايت. يمكن أن تعرض وظيفة المسح خمس قيم: 0 - إذا كانت 4 بايتات معتادة من دفق الفيديو لإعادة التعبئة ، 1 - إذا كانت رأس كتلة دفق الفيديو للإطار المرجعي ، 2 - إذا كان عنوان كتلة دفق الفيديو للإطار المضغوط ، 3 - إذا كان رأس كتلة دفق الصوت ، 4 - إذا كان كتلة "تالفة" ليتم تجاهلها أثناء إعادة التعبئة. نادر جدا جدا ، لكنه حدث. الكتلة التالفة (كما أسميتها) هي رأس مثل "\ 0 \ 0 \ 0 \ 0 H264" ، حيث "\ 0" هو صفر بايت. يتجاهل أداة إعادة التعبئة المنتظمة كتلًا من هذا النوع. بالطبع ، قد يتبين أن محتويات مثل هذه الكتلة تعمل بشكل جيد ، لكنني أتجاهل هذه الكتل لتقريب برنامجي من البرنامج القياسي.

في الوظيفة الرئيسية ، بالإضافة إلى تنظيم الدلائل ، تتم قراءة ملف الإدخال بواسطة وظيفة المسح. اعتمادًا على ما أعادت هذه الوظيفة ، تحدث إجراءات أخرى. إذا كانت هذه هي رؤوس تدفقات الفيديو ، فإن الرؤوس المقابلة تتشكل في ملف avi الناتج. هناك يطلق عليهم بشكل مختلف: "00db" هو عنوان كتلة تدفق الفيديو للإطار المرجعي ، و "00dc" للإطار المضغوط. بعد عملية إعادة التعبئة (إعادة كتابة الكلمات) قبل الرأس الجديد الذي تمت مواجهته حديثًا ، يتم حساب حجم المحتويات المعاد تعبئتها ويتم كتابة هذه القيمة في الحقل الذي يتبع رأس الدفق الذي تمت معالجته للتو. في حالة مواجهة رأس دفق صوتي أثناء المسح ، يتم إنشاء اسم الرأس "03wb" في ملف avi الناتج ويتم فك دفق الصوت من ADPCM إلى PCM في الحلقة في نفس الوقت الذي يتم فيه كتابة المحتويات التي تم فك تشفيرها إلى ملف avi. إلى جانب كل ما سبق ، يتم تسجيل معلومات موجزة (جدول المحتويات) في "فهرس" ملف فهرس مؤقت. لا يمكنك القيام بوظيفة المسح ، ولكن اكتب كل شيء في الوظيفة الرئيسية. ولكن بعد ذلك سيكون البرنامج مرهقًا للغاية ويصعب قراءته تقريبًا.

في نهاية العملية بأكملها ، عندما ينتهي ملف الإدخال "264" ، قبل الانتقال إلى ملف جديد ، يكمل البرنامج بكفاءة جميع العمليات. أولاً ، يتم تعديل بعض الحقول في رأس ملف avi ، وتعتمد قيمها على حجم وعدد التدفقات المقروءة ، ثم يتم إرفاق محتويات ملف "الفهرس" المؤقت بملف avi الذي تم الانتهاء منه تقريبًا ، والذي يتم حذفه بعد ذلك. بعد هذه العمليات ، يصبح ملف avi جاهزًا للتشغيل.

أثناء تشغيل البرنامج ، يتم إجراء تصور نصي في سطر الأوامر ، والذي يعرض الدليل الحالي والملف بالإضافة إلى رقم كتلة دفق الفيديو لكل إطار مرجعي والنقطة الزمنية المقابلة للفيديو بالدقائق والثواني. وإذا لم يكن لملف الإدخال اسم عشوائي ، ولكن الاسم الأصلي (الذي يحتوي على رقم القناة وتاريخ ووقت بدء التسجيل) ، فسيحدث تصور أكثر تفاعلية استنادًا إلى حساب التاريخ والوقت.

عند اختبار البرنامج وتصحيحه ، كانت المشاكل الرئيسية التي واجهتني أثناء العمل مع فك تشفير الصوت. لم يعمل الحساب البسيط بشكل صحيح إذا ، عندما أعلن عن المتغيرات في وظيفة فك التشفير ، لم أكتب الأنواع بشكل صحيح. وبسبب هذا ، تم كسر بعض كتل تدفقات الصوت ، وكانت هناك نقرات بالأذن. عدد قليل من حقول العناوين غير المفهومة لملف 264 الأصلي الذي لم أستطع تبين أنه غير حساس للنتيجة. على عكس البرنامج العادي ، لا يرمي البرنامج آخر كتلة تدفق غير مكتملة من عملية إعادة التعبئة. على الرغم من أن غيابها لن يلعب أي دور عملي. هناك برنامج عادي آخر ، على عكس برنامجي ، يترك وراءه كمية صغيرة من "القمامة" (هذه هي محتويات آخر دفق) في نهاية ملف avi بعد الفهارس. لكل هذا ، يلعب الفيديو نفسه تقريبًا. ويقوم البرنامج بإعادة التعبئة لنفس الفترة الزمنية للبرنامج العادي.

في الختام ، سأقدم توضيحات توضح هيكل تنظيم التدفقات في ملف .264 (في محرر WinHex hex) باستخدام أحد الملفات كمثال وظهور برنامج RiffPad مع ملف avi المعاد فتحه فيه. يبسط هذا البرنامج إلى حد كبير عملية دراسة بنية ملف AVI. يوضح بوضوح الهيكل الهرمي ، ويظهر محتوى البايت لكل عضو في الهيكل ، وحتى يفسر بذكاء محتويات الرؤوس في شكل قائمة من المعلمات. توضح الصورة ، على وجه الخصوص ، حقيقة أن محتويات دفق الفيديو يتم استبدالها بدون تغييرات.

تطوير محول فيديو من 264 إلى avi ل Dashcam QCM-08DL

More articles: